Pythagoras Coordinates Worksheet A The worksheet is in

Printing To print handouts from slides Select the slide from the left. Then click:

Pythagoras’ Theorem with Coordinates 1) Mark point B at (8, 6). Sketch a triangle

Pythagoras’ Theorem with Coordinates 1) Mark point B at (8, 6). B Sketch a

Pythagoras’ Theorem with Coordinates D F 1) Mark point B at (8, 6). C

Pythagoras’ Theorem with Coordinates A Does it matter if the horizontal or vertical distances

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated

Slides: 9

Download presentation

Pythagoras – Coordinates – Worksheet A The worksheet is in 2 sizes.

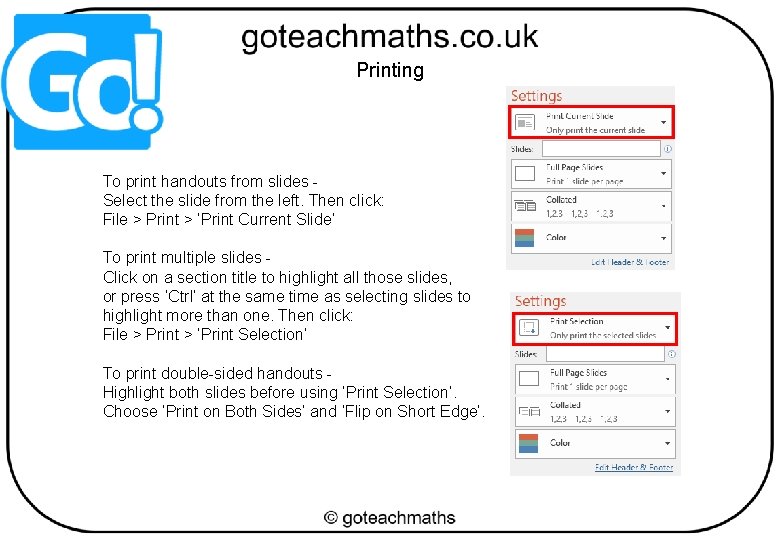
Printing To print handouts from slides Select the slide from the left. Then click: File > Print > ‘Print Current Slide’ To print multiple slides Click on a section title to highlight all those slides, or press ‘Ctrl’ at the same time as selecting slides to highlight more than one. Then click: File > Print > ‘Print Selection’ To print double-sided handouts Highlight both slides before using ‘Print Selection’. Choose ‘Print on Both Sides’ and ‘Flip on Short Edge’.

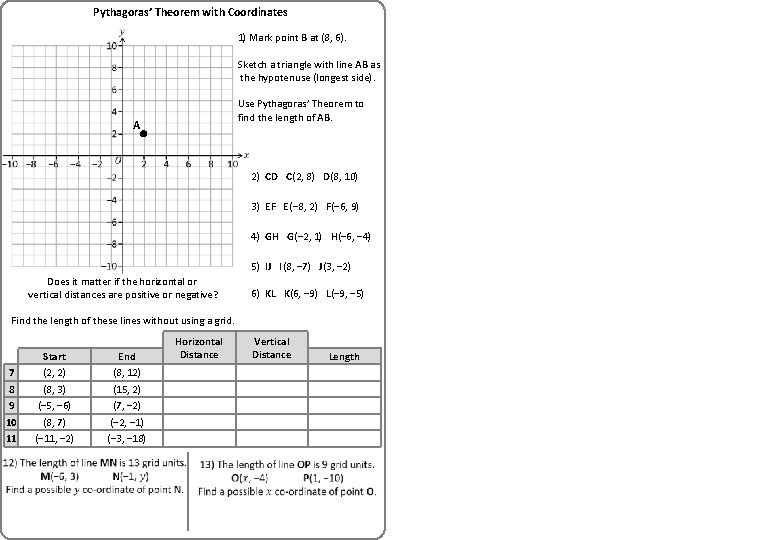
Pythagoras’ Theorem with Coordinates 1) Mark point B at (8, 6). Sketch a triangle with line AB as the hypotenuse (longest side). Use Pythagoras’ Theorem to find the length of AB. A 2) CD C(2, 8) D(8, 10) 3) EF E(− 8, 2) F(− 6, 9) 4) GH G(− 2, 1) H(− 6, − 4) 5) IJ I(8, − 7) J(3, − 2) Does it matter if the horizontal or vertical distances are positive or negative? 6) KL K(6, − 9) L(− 9, − 5) Find the length of these lines without using a grid. 7 8 9 10 11 Start (2, 2) (8, 3) (− 5, − 6) (8, 7) (− 11, − 2) End (8, 12) (15, 2) (7, − 2) (− 2, − 1) (− 3, − 18) Horizontal Distance Vertical Distance Length

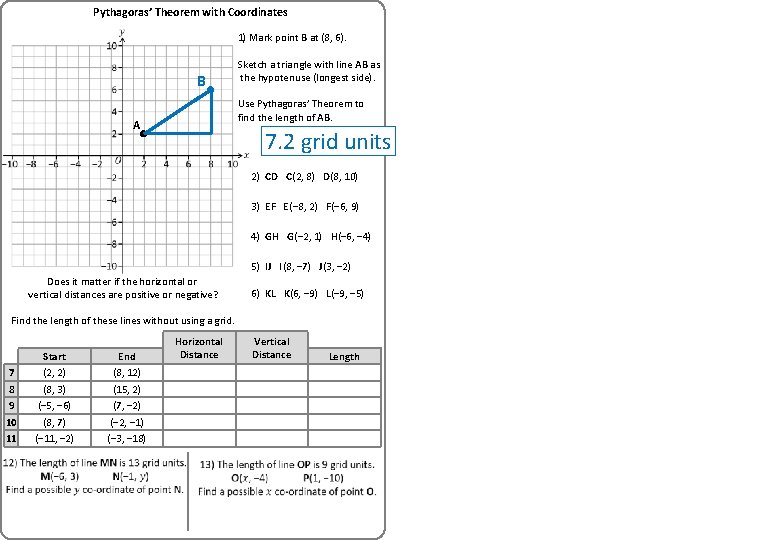
Pythagoras’ Theorem with Coordinates 1) Mark point B at (8, 6). B Sketch a triangle with line AB as the hypotenuse (longest side). Use Pythagoras’ Theorem to find the length of AB. A 7. 2 grid units 2) CD C(2, 8) D(8, 10) 3) EF E(− 8, 2) F(− 6, 9) 4) GH G(− 2, 1) H(− 6, − 4) 5) IJ I(8, − 7) J(3, − 2) Does it matter if the horizontal or vertical distances are positive or negative? 6) KL K(6, − 9) L(− 9, − 5) Find the length of these lines without using a grid. 7 8 9 10 11 Start (2, 2) (8, 3) (− 5, − 6) (8, 7) (− 11, − 2) End (8, 12) (15, 2) (7, − 2) (− 2, − 1) (− 3, − 18) Horizontal Distance Vertical Distance Length

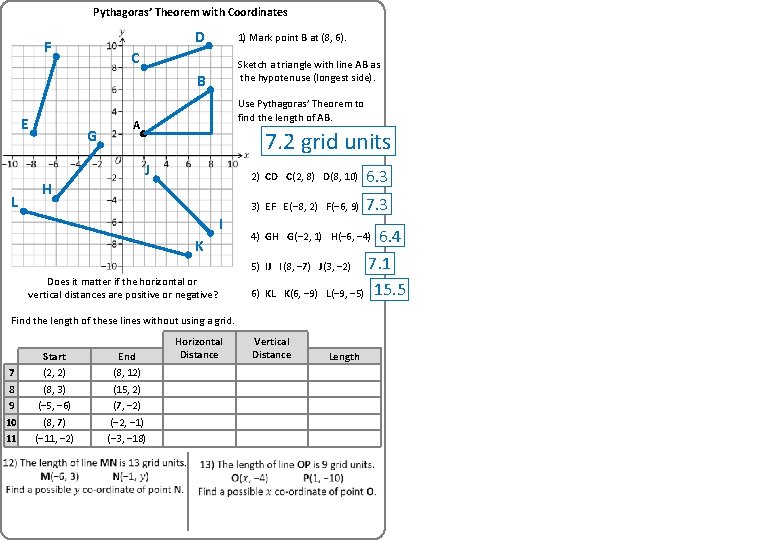
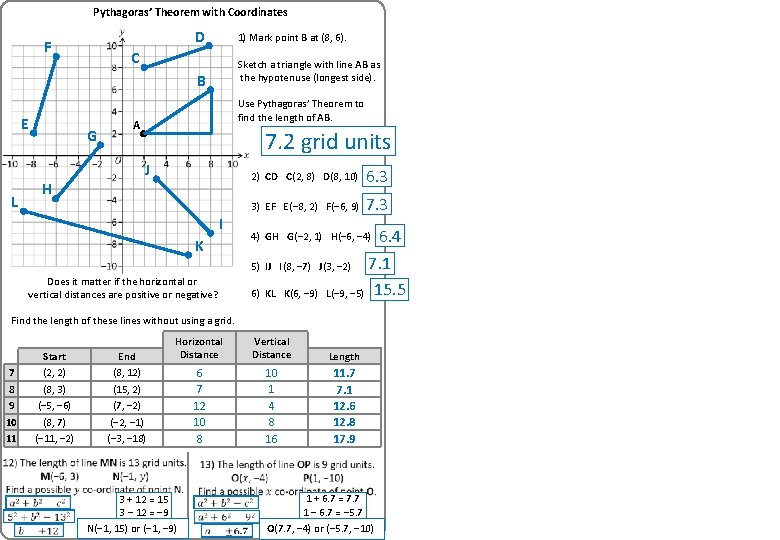
Pythagoras’ Theorem with Coordinates D F 1) Mark point B at (8, 6). C Sketch a triangle with line AB as the hypotenuse (longest side). B E G Use Pythagoras’ Theorem to find the length of AB. A 7. 2 grid units J L H I K 2) CD C(2, 8) D(8, 10) 6. 3 3) EF E(− 8, 2) F(− 6, 9) 7. 3 4) GH G(− 2, 1) H(− 6, − 4) 6) KL K(6, − 9) 7. 1 L(− 9, − 5) 15. 5 Vertical Distance Length 5) IJ I(8, − 7) J(3, − 2) Does it matter if the horizontal or vertical distances are positive or negative? Find the length of these lines without using a grid. 7 8 9 10 11 Start (2, 2) (8, 3) (− 5, − 6) (8, 7) (− 11, − 2) End (8, 12) (15, 2) (7, − 2) (− 2, − 1) (− 3, − 18) Horizontal Distance 6. 4

Pythagoras’ Theorem with Coordinates D F 1) Mark point B at (8, 6). C Sketch a triangle with line AB as the hypotenuse (longest side). B E G Use Pythagoras’ Theorem to find the length of AB. A 7. 2 grid units J L H I K 2) CD C(2, 8) D(8, 10) 6. 3 3) EF E(− 8, 2) F(− 6, 9) 7. 3 4) GH G(− 2, 1) H(− 6, − 4) 6) KL K(6, − 9) 7. 1 L(− 9, − 5) 15. 5 Horizontal Distance Vertical Distance Length 6 7 12 10 8 10 1 4 8 16 11. 7 7. 1 12. 6 12. 8 17. 9 5) IJ I(8, − 7) J(3, − 2) Does it matter if the horizontal or vertical distances are positive or negative? Find the length of these lines without using a grid. 7 8 9 10 11 Start (2, 2) (8, 3) (− 5, − 6) (8, 7) (− 11, − 2) End (8, 12) (15, 2) (7, − 2) (− 2, − 1) (− 3, − 18) 6. 4 3 + 12 = 15 3 − 12 = − 9 N(− 1, 15) or (− 1, − 9) 1 + 6. 7 = 7. 7 1 − 6. 7 = − 5. 7 O(7. 7, − 4) or (− 5. 7, − 10)

Pythagoras’ Theorem with Coordinates A Does it matter if the horizontal or vertical distances are positive or negative? Pythagoras’ Theorem with Coordinates 1) Mark point B at (8, 6). Sketch a triangle with line AB as the hypotenuse (longest side). Use Pythagoras’ Theorem to find the length of AB. 2) CD C(2, 8) D(8, 10) 3) EF E(− 8, 2) F(− 6, 9) 4) GH G(− 2, 1) H(− 6, − 4) 5) IJ I(8, − 7) J(3, − 2) 7 8 9 10 11 End (8, 12) (15, 2) (7, − 2) (− 2, − 1) (− 3, − 18) Horizontal Distance Does it matter if the horizontal or vertical distances are positive or negative? 6) KL K(6, − 9) L(− 9, − 5) Find the length of these lines without using a grid. Start (2, 2) (8, 3) (− 5, − 6) (8, 7) (− 11, − 2) A 6) KL K(6, − 9) L(− 9, − 5) Find the length of these lines without using a grid. Vertical Distance Length 7 8 9 10 11 Start (2, 2) (8, 3) (− 5, − 6) (8, 7) (− 11, − 2) End (8, 12) (15, 2) (7, − 2) (− 2, − 1) (− 3, − 18) Horizontal Distance Vertical Distance Length

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk