Pytagoras setning Undervisningsopplegg laget av Johan Nygaard for

Pytagoras’ setning Undervisningsopplegg laget av Johan Nygaard for Vitenfabrikken i Sandnes

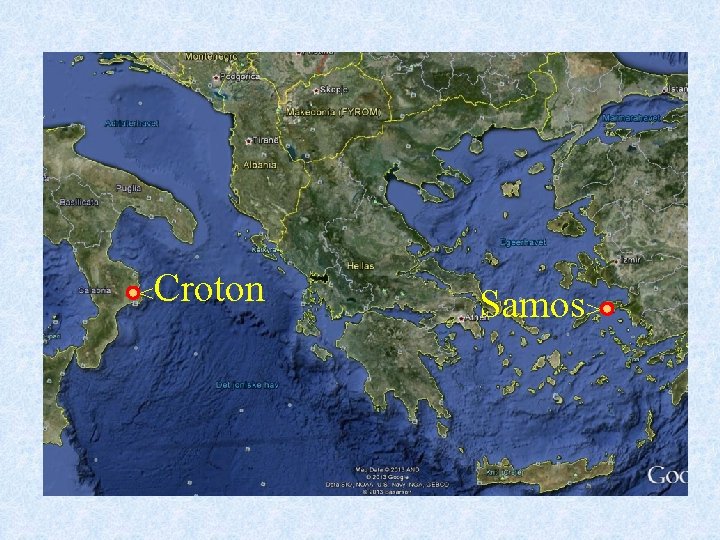
Pytagoras levde ca 569 – 475 f. Kr. Han var født og vokste opp på den greske øya Samos i Egeerhavet. Pytagoras forsøkte seg som lærer på hjemstedet. Han arbeidet med både matematikk, musikk og filosofi, og han fikk mange elever. Han kom etter hvert på kant med den lokale herskeren, og han flyttet derfor til Croton i Sør-Italia. Her bodde han hos sin venn Milo, og han giftet seg med Milos datter Teano.

< Croton Samos>

Det pytagoreiske samfunn I Croton grunnla Pytagoras en skole og et filosofisk og religiøst brorskap som ble kalt ”Det pytagoreiske samfunn”. De "innerste" medlemmene av samfunnet bodde alltid sammen med Pytagoras. De måtte være vegetarianere, og de fikk ikke ha personlige eiendeler. Medlemmene ble kalt pytagoreerne, og de studerte filosofi, matematikk, astronomi og musikk. Pytagoreerne forsøkte å holde arbeidet sitt mest mulig hemmelig, men de fikk likevel stor innflytelse på antikkens filosofi.

Det pytagoreiske samfunn Pentagrammet ble pytagoreernes hemmelige tegn. Det består av diagonalene i en regulær femkant. Vi henter noen linjestykker fra pentagrammet: Dersom vi dividerer en av disse lengdene med den påfølgende lengden, får vi det gylne snitt.

Pytagoras sa: ”Alt er tall. ” Nå benytter vi arabiske tall. Pytagoras brukte greske tall (bokstaver). Greske tall på Abel-loftet

Pytagoras Perfekte tall Pytagoras kalte noen tall for perfekte tall. Et tall kalles perfekt hvis summen av alle tall som går opp i tallet, blir lik tallet selv. Et eksempel er 6, fordi 1+2+3=6. De tre neste perfekte tallene er 28, 496 og 8128. (1+2+4+7+14=28 og 1+2+4+8+16+31+62+124+248=496)

Pytagoras Pytagoreerne oppdaget også noe de kalte for vennlige tallpar: 220 kan divideres med 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, og 110. Summen av disse blir 284 kan divideres med 1, 2, 4, 71 og 142. Summen av disse blir 220 og 284 kalles derfor et vennlig tallpar. Andre vennlige tallpar er: 1184 og 1210, 17296 og 18416, 9363584 og 9437056.

Pytagoras Rasjonale og irrasjonale tall Pytagoras mente at alle tall kunne skrives som brøker eller desimaltall, altså rasjonale tall. Pytagoreerne hadde problemer med å akseptere at det fantes tall som ikke var rasjonale, og π. som for eksempel: Slike tall kaller vi for irrasjonale tall.

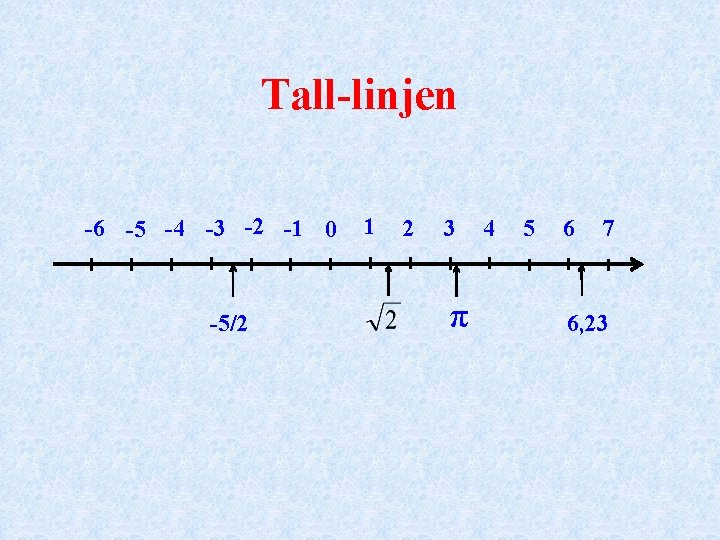
Tall-linjen -6 -5 -4 -3 -2 -1 0 -5/2 1 2 3 π 4 5 6 7 6, 23

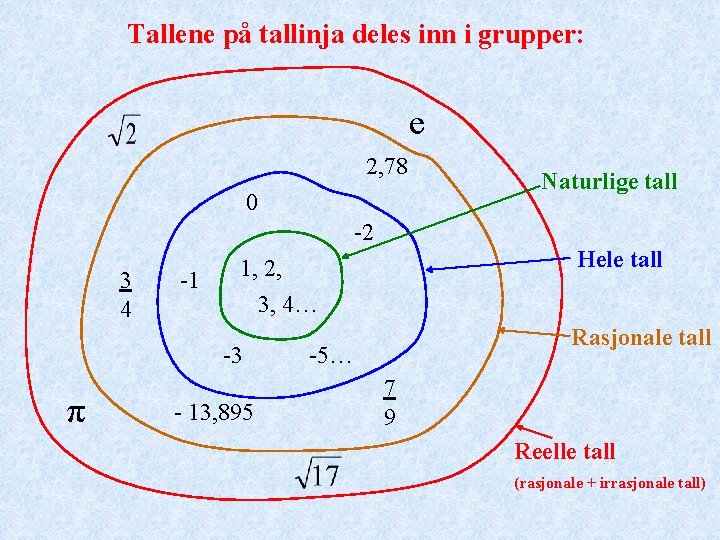
Tallene på tallinja deles inn i grupper: e 2, 78 0 Naturlige tall -2 3 4 -1 -3 π Hele tall 1, 2, 3, 4… - 13, 895 Rasjonale tall -5… 7 9 Reelle tall (rasjonale + irrasjonale tall)

Pytagoras Pytagoreerne fant ut at når vi spiller på en streng, vil tonene lyde harmonisk dersom vi endrer strengens lengde med brøkdeler som for eksempel: 1/2, 2/3, 3/4, 4/5, 8/9. L 1· L c 4/5· L e 2/3· L g 1/2· L c’ Den pyatgoreiske skalaen har gitt gjenlyd helt opp til vår tids musikk.

Pytagoras var mest kjent for Pytagoras’ setning: ”I en rettvinklet trekant er kvadratet på hypotenusen lik summen av kvadratene på katetene. ” Sammenhengen mellom lengdene av sidene i en rettvinklet trekant var imidlertid kjent lenge før Pytagoras' tid. Både de gamle babylonerne og kineserne kjente til og brukte setningen.

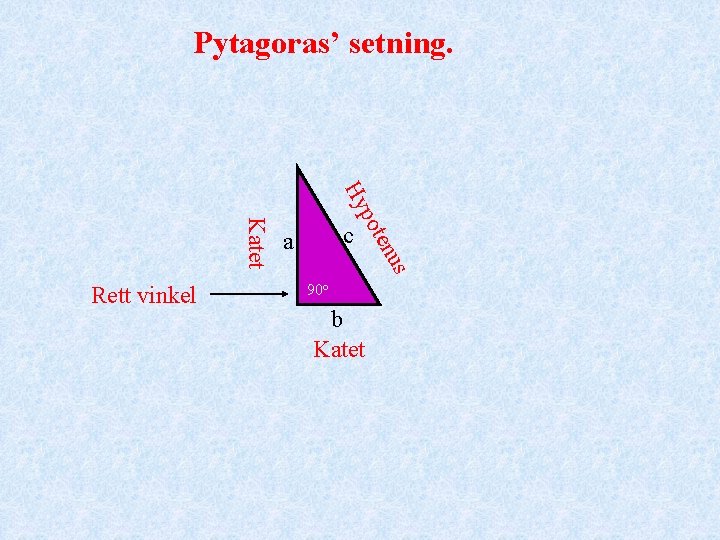
Pytagoras’ setning. us ten po Hy Katet Rett vinkel c a 90 o b Katet

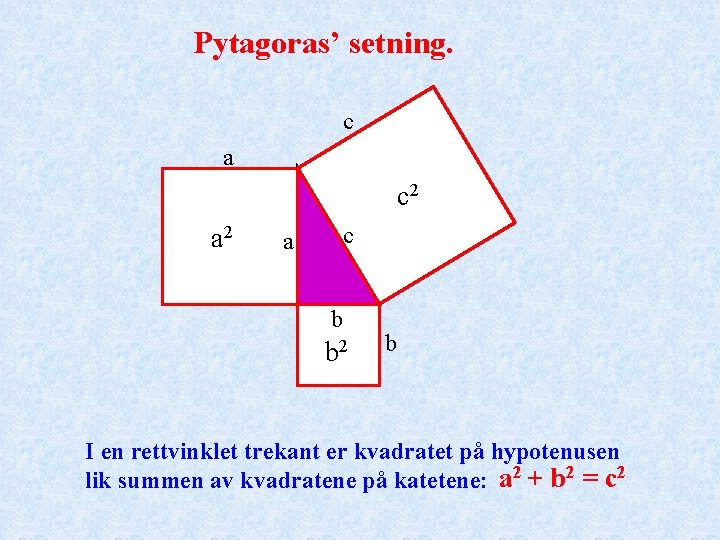
Pytagoras’ setning. c a c 2 a 2 c a b b 2 b I en rettvinklet trekant er kvadratet på hypotenusen lik summen av kvadratene på katetene: a 2 + b 2 = c 2

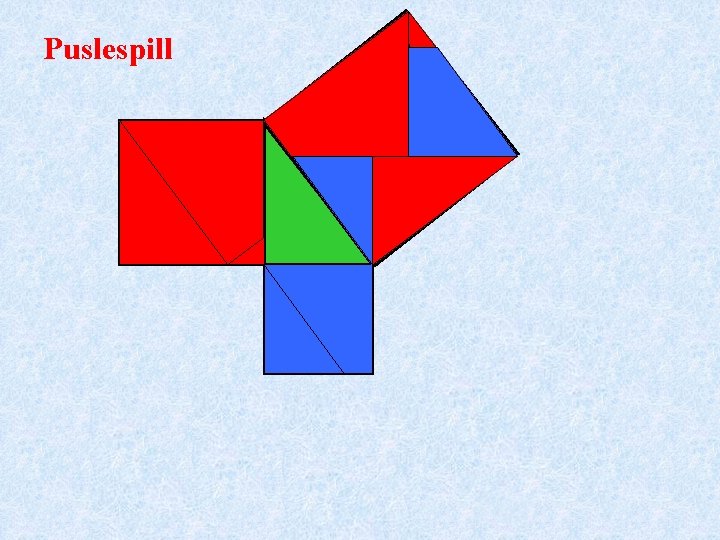
På Abel-loftet finnes et puslespill som viser at Pytagoras sin setning er riktig.

Puslespill

Eksempel på bruk av Pytagoras’ setning. Når vi kjenner to av sidene kan vi regne ut den tredje siden. a=4 c=? b=3 a 2 + b 2 = c 2 gir oss følgende utregning: c 2 = 42 + 32 = 16 + 9 = 25 og dermed

Et tau med knuter kan brukes til å lage 90 o 12 knuter med lik avstand

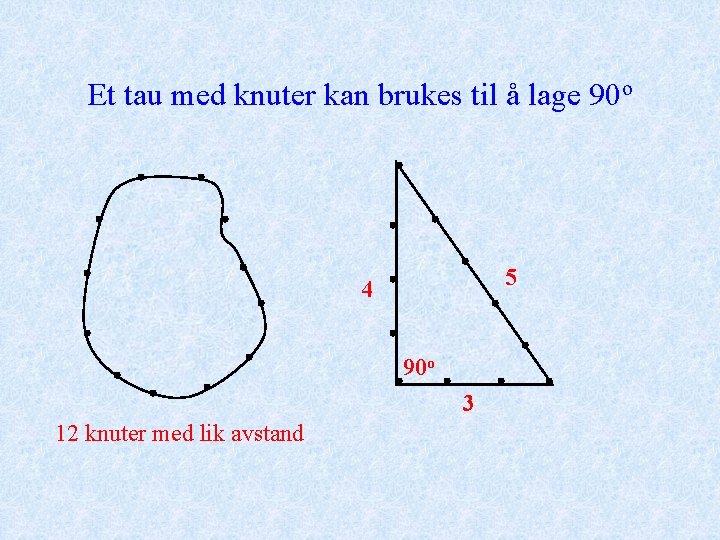
Et tau med knuter kan brukes til å lage 90 o 5 4 90 o 3 12 knuter med lik avstand

Eksempel nr 2 på bruk av Pytagoras’ setning. Når vi kjenner to av sidene kan vi regne ut den tredje siden. c=14, 7 a=? b=5, 4 a 2 = c 2 – b 2 gir oss følgende utregning: a 2 = 14, 72 – 5, 42 = 216, 09 – 29, 16 = 186, 93 og dermed

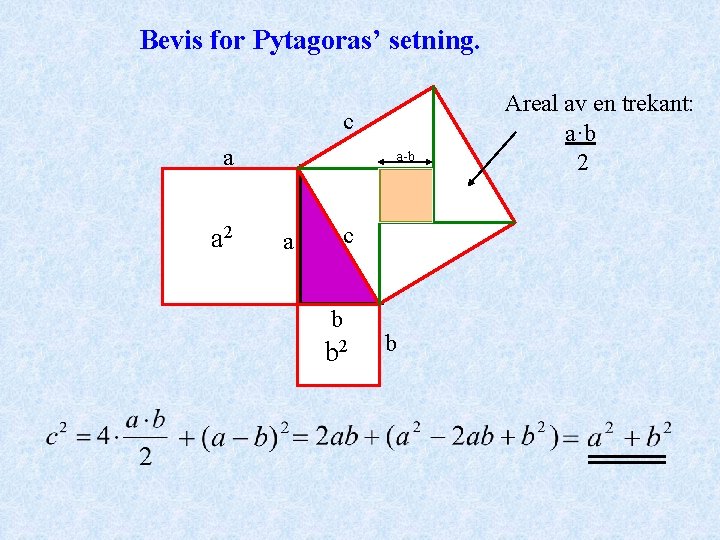
Bevis for Pytagoras’ setning. c a a-b c 2 a 2 c a b b 2 b Areal av en trekant: a·b 2

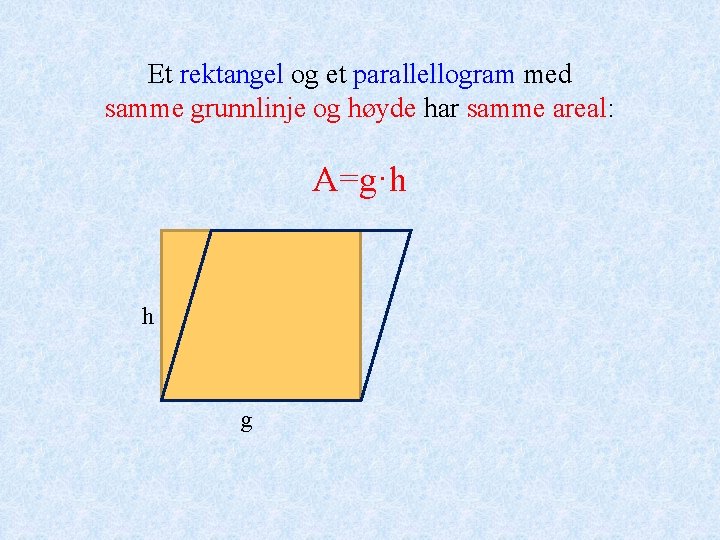
Et rektangel og et parallellogram med samme grunnlinje og høyde har samme areal: A=g·h h g

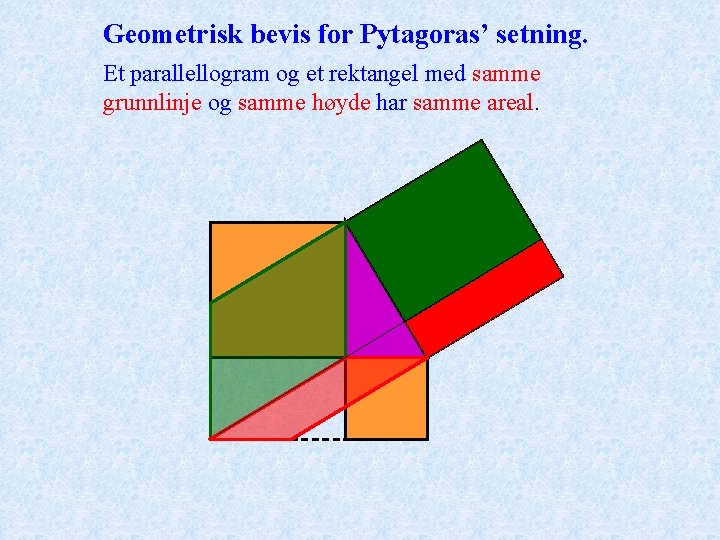
Geometrisk bevis for Pytagoras’ setning. Et parallellogram og et rektangel med samme grunnlinje og samme høyde har samme areal.

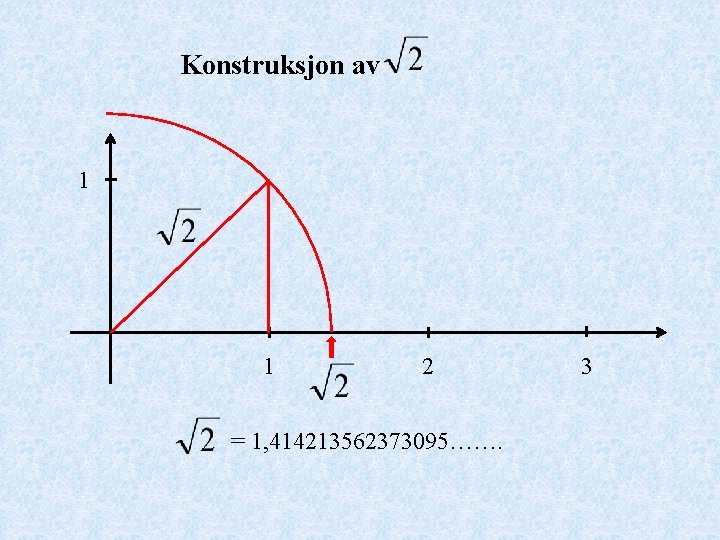
Konstruksjon av 1 1 2 = 1, 414213562373095……. 3

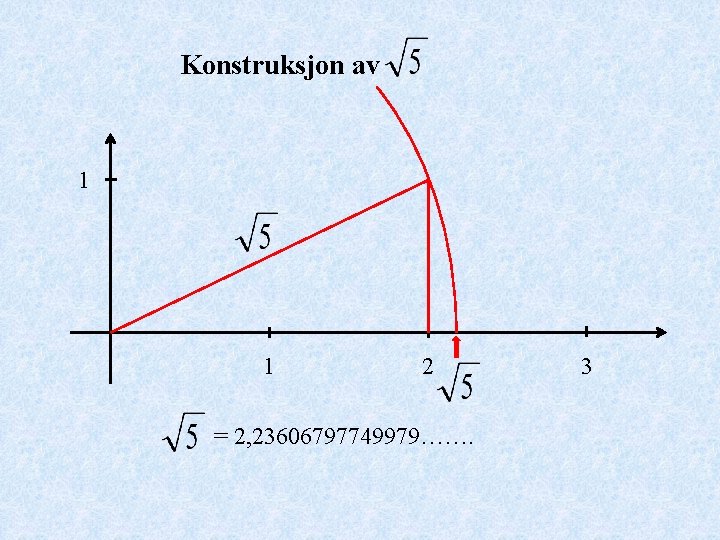
Konstruksjon av 1 1 2 = 2, 23606797749979……. 3

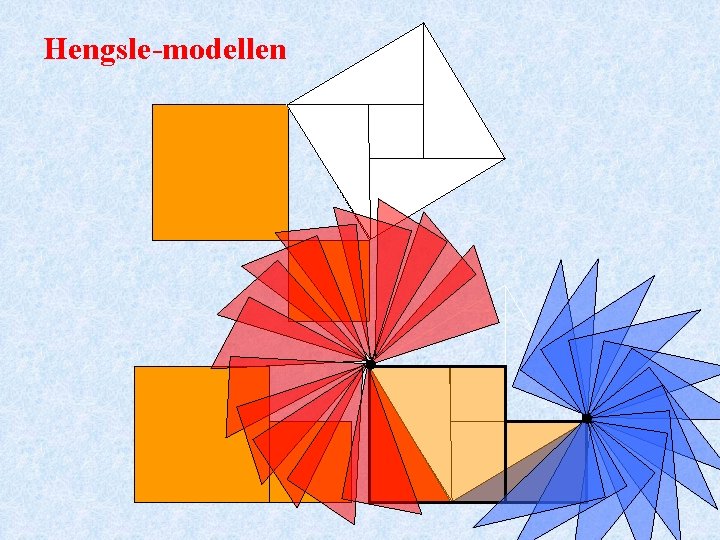
På Abel-loftet finnes en ”hengslemodell” som viser at Pytagoras sin setning er riktig.

Hengsle-modellen

Pytagoreiske tripler Tall-trippelet (3, 4, 5) passer i Pytagoras’ setning fordi: 32 + 42 = 52 Trippelet (5, 12, 13) passer også: 52 + 122 = 132 Kan du finne flere tripler? Her noen: Katet 6 8 Katet 8 15 Hypotenus 10 17 12 7 16 24 20 25 Det finnes uendelig mange tripler som passer.

Hvor mange tall-tripler passer i likningene a 3 + b 3 = c 3 eller a 4 + b 4 = c 4 ? På 1600 -tallet framsatte Pierre de Fermat sin berømte påstand: Fermat’s siste setning: Det finnes ingen positive heltall (a, b, c) som passer i likningen an + bn = cn når n > 2. Denne påstanden ble først bevist i 1995 av den britiske matematikeren Andrew Wiles. Beviset er på over 130 sider, og det er meget vanskelig.

Slutt