Pushdown Automata Relationship to eNFA Actions of the

Pushdown Automata Relationship to e-NFA Actions of the PDA Languages of the PDA 1

PDA’s related to e-NFA’s PDA’s are ε-NFA’s with additional ability to manipulate a stack. Moves are determined by: 1. The current state of the e-NFA, 2. The current input symbol (or ε), and 3. The current symbol on top of the stack. 2

PDA’s related to e-NFA’s Being non-deterministic, the PDA can simultaneously explore several actions. In each action, the PDA can: 1. Change state 2. Replace the top symbol on the stack by zero or more symbols. • Zero symbols = “pop” • One symbol = “push” 3

For a formal definition of a PDA, list the following components in order: 1. 2. 3. 4. Q=finite set of states Σ=input alphabet Γ= stack alphabet δ=transition function 5. q 0=start state 6. Z 0=start symbol 7. F=set of final states Example: P=({p, q}, {0, 1}, {Z 0, X}, d, q, Z 0, {p}) 4

Conventions on symbols a, b, … are usually input symbols. X, Y, Z, …are usually stack symbols. w, x, y, z, … are strings of input symbols , , … are strings of stack symbols. ε (empty string) may be used at any point as next input (i. e. , a spontaneous transition) 5

The Transition Function Takes three arguments: 1. q is a state in Q 2. a (an input symbol) or ε. 3. Z is top symbol of stack δ(q, a, Z ) is a set of zero or more actions of the form (p, ) where p is a state in Q and is a string of stack symbols 6

Actions of the PDA If δ(q, a, Z ) contains (p, ) among its actions, then the PDA: 1. Changes its state to p. 2. Removes a from the front of the input 3. Replaces Z on the top of the stack by 7

Sting acceptance by final state L(P) denotes the language defined by PDA P that accepts by final state 1. Input is consumed and P is in an accepting state. 2. Content of stack at acceptance is irrelevant 8

Sting acceptance by empty stack N(P) denotes a language of strings that PDA P consumes in actions that empty its stack. 1. The state of P when actions are complete is irrelevant. 2. Formal definition of P may or may not involve accepting states. 3. If the transition function of P does not allow the stack to empty, then N(P)=nil. 4. If P has accepting states, then a transition function can be defined such that N(P)=L(P). 9

Example of PDA Design a PDA to accept {0 n 1 n | n > 1}. Design principles: 1. q = start state and where we are if we have seen only 0’s in the input so far. 2. p = state after we’ve seen at least one 1 and where we remain if the inputs are 1’s. 3. f = accepting state. 10

PDA to accept {0 n 1 n | n > 1} The stack symbols: Z 0 = start symbol of the stack. Whenever Z 0 is on top of the stack, we have counted the same number of 1’s as 0’s (initially count is zero) X = marker pushed onto stack every time 0 is the input (i. e. , counts the number of 0’s) 11

PDA of language {0 n 1 n | n > 1} Transition function: (1) δ(q, 0, Z 0) = {(q, XZ 0)}. Replace Z 0 by XZ 0 (2) δ(q, 0, X) = {(q, XX)}. Replace X by XX. Actions 1 & 2 cause one X to be pushed onto the stack for each 0 read from the input. (3) δ(q, 1, X) = {(p, ε)}. When we see a 1, go to state p and pop one X. (4) δ(p, 1, X) = {(p, ε)}. Pop another X. (5) δ(p, ε, Z 0) = {(f, Z 0)}. Spontaneous transition to accepting state when Z 0 returns to the top of stack. (only spontaneous transition) 12

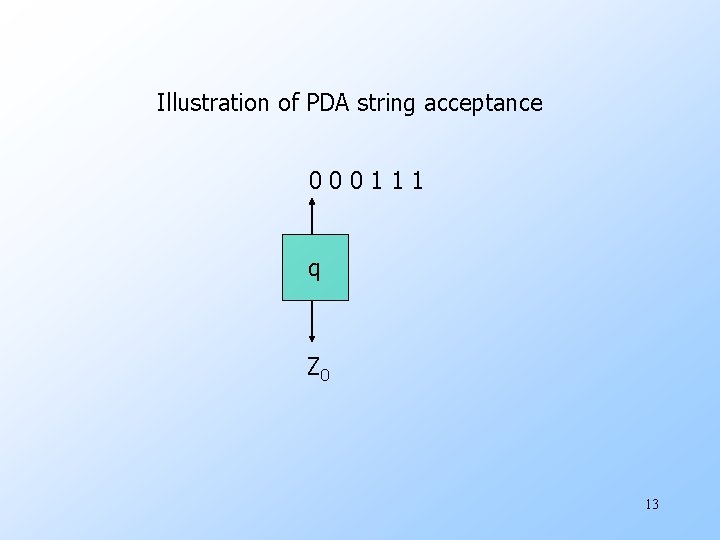
Illustration of PDA string acceptance 000111 q Z 0 13

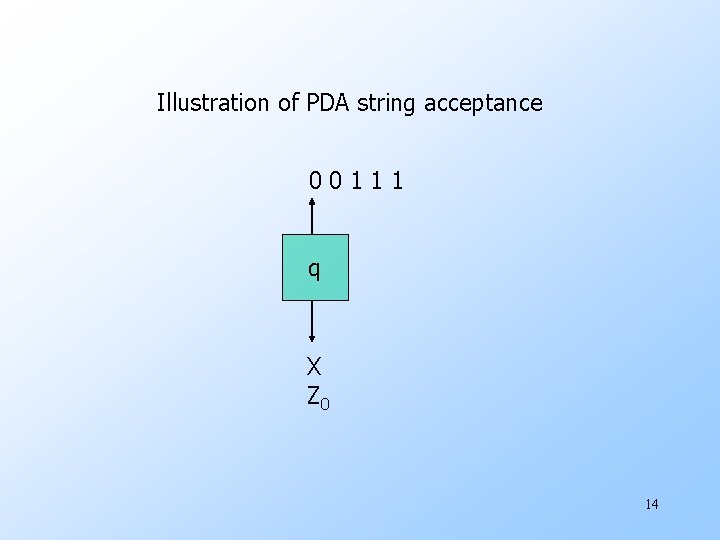
Illustration of PDA string acceptance 00111 q X Z 0 14

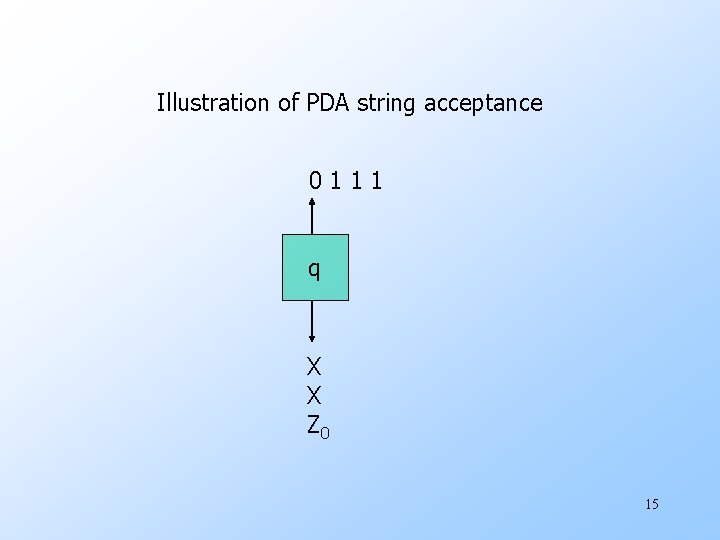
Illustration of PDA string acceptance 0111 q X X Z 0 15

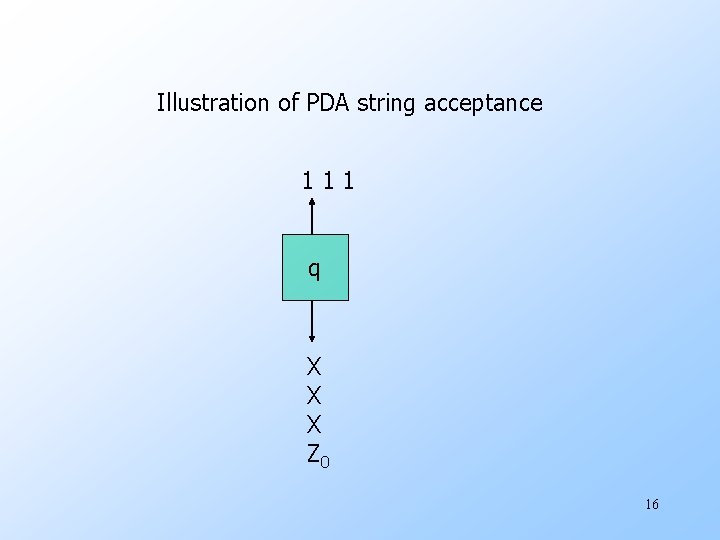
Illustration of PDA string acceptance 111 q X X X Z 0 16

Illustration of PDA string acceptance 11 p X X Z 0 17

Illustration of PDA string acceptance 1 p X Z 0 18

Illustration of PDA string acceptance p Z 0 19

Illustration of PDA string acceptance f Z 0 20

Instantaneous Description(ID) An ID is a triple (q, w, ), where: 1. q is the current state. 2. w is remaining input, next input at left. 3. is the stack contents, top at the left. Be careful not to confuse IDs with rules in the transition function when w and are single characters. 21

The “Goes-To” Relation Denote ID i “goes to” ID j in one of the actions of a PDA by i ⊦ j. (q, aw, X )⊦(p, w, ) for any w and , if δ(q, a, X) contains action (p, ). Extend ⊦ to ⊦*, meaning “zero or more actions, ” by: Basis: i⊦*i Induction: If i⊦*j and j⊦k, then i⊦*k 22

Use numbered “Goes-To” Relations If ID i goes to ID j by action k in the transition function, add k as a superscript on ID i. (q, aw, X )k⊦(p, w, ) for any w and , if kth action in the transition table is δ(q, a, X) = (p, ). 23

Assignment 14 Exercise 6. 2. 5 a text p 242 Number the moves in the transition function 1 to 11. Down the columns preferred. Use numbered IDs to test acceptance of string bab by final state. Rationale behind the transition function is not obvious. Keep searching for allowed actions that move toward string consumption and transition to final state 24

Numbered actions in transition function of PDA that accepts strings {0 n 1 n | n > 1} by final state (1) (2) (3) (4) (5) δ(q, δ(p, 0, Z 0) = {(q, XZ 0)}. Consume 0, push X 0, X) = {(q, XX)}. Consume 0, push X 1, X) = {(p, ε)}. Consume 1, q->p, pop X 1, X) = {(p, ε)}. Consume 1, pop X. ε, Z 0) = {(f, Z 0)}. Spontaneous p->f Test 000111 for acceptance using numbered goesto statements Do on board 25

Test 000111 for acceptance by PDA for {0 n 1 n|n>1} (q, 000111, Z 0)1⊦(q, 00111, XZ 0)2⊦ (q, 0111, XXZ 0)2⊦(q, 111, XXXZ 0)3⊦ (p, 11, XXZ 0)4⊦(p, 1, XZ 0)4⊦(p, ε, Z 0)5⊦ (f, ε, Z 0) What would happen on input 0001111? Do on board 26

Legal because a PDA can use ε input even if input remains. (q, 0001111, Z 0)1⊦(q, 001111, XZ 0)2⊦ (q, 01111, XXZ 0)2⊦(q, 1111, XXXZ 0)3⊦ (p, 111, XXZ 0)4⊦(p, 11, XZ 0)4⊦(p, 1, Z 0)5⊦(f, 1, Z 0) • The only action possible when in state p and Z 0 is at the top of the stack is spontaneous transition of the final state. • Dead end. No action in transition table that can modify the last ID. • 0001111 is not accepted, because the input is not completely consumed. 27

Change the PDA for {0 n 1 n|n >1} to create a PDA for language {0 n 1 n+1|n>1} New PDA must accept all and only strings of {0 n 1 n+1|n>1} Solution based on the same logic as PDA for {0 n 1 n|n >1} Do on board 28

Change the PDA for {0 n 1 n|n >1} to create a PDA for language {0 n 1 n+1|n>1} (1) δ(q, XXZ 0 (2) δ(q, (3) δ(q, (4) δ(p, (5) δ(p, 0, Z 0) = {(q, XXZ 0)}. Consume 0, replace Z 0 with 0, X) = {(q, XX)}. Consume 0, push X 1, X) = {(p, ε)}. Consume 1, q->p, pop X 1, X) = {(p, ε)}. Consume 1, pop X. ε, Z 0) = {(f, Z 0)}. Spontaneous p->f 29

Use |-* to define L(P) If P is a PDA, then L(P) denotes the set of strings w such that (q 0, w, Z 0) ⊦*(f, ε, ) for final state f and any . Acceptance/rejection determined by state of P when all input consumed irrespective of stack content. 30

Use |-* to define N(P) If P is a PDA, then N(P) denotes the set of strings w such that (q 0, w, Z 0) ⊦*(q, ε, ε) for any state q. All input consumed, stack empty, current state of P is irrelevant. 31

Ex 6. 1. 1 pp 233 -234 P=({p, q}, {0, 1}, {Z 0, X}, d, q, Z 0, {p}) 7 actions in the transition table: (1) δ(q, 0, Z 0) = {(q, XZ 0)} consume 0, push X (2) δ(q, 0, X) = {(q, XX)} consume 0, push X (3) δ(q, 1, X) = {(q, X)} consume 1 (4) δ(q, e, X) = {(p, ε)} spontaneous q->p pop X (5) δ(p, e, X) = {(p, ε)} spontaneous pop X (6) δ(p, 1, X) = {(p, XX)} consume 1 push X (7) δ(p, 1, Z 0) = {(p, ε)} consume 1 pop Z 0 Test string 01 for acceptance by final state and/or empty stack. Do on board 32

Ex 6. 1. 1 a p 234 input 01 (q, 01, Z 0)1⊦(q, 1, XZ 0)3⊦(q, e, XZ 0)4⊦ (p, e, Z 0) accepted by final state only (q, 01, Z 0)1⊦(q, 1, XZ 0)4⊦(p, 1, Z 0)7⊦(p, e, e) accepted by final state and empty stack (q, 01, Z 0)1⊦(q, 1, XZ 0)3⊦(q, e, XZ 0)4 no way to stay in q and empty stack 33

34