Pushdown Automata PDAs 1 Pushdown Automaton PDA Input

Pushdown Automata PDAs 1

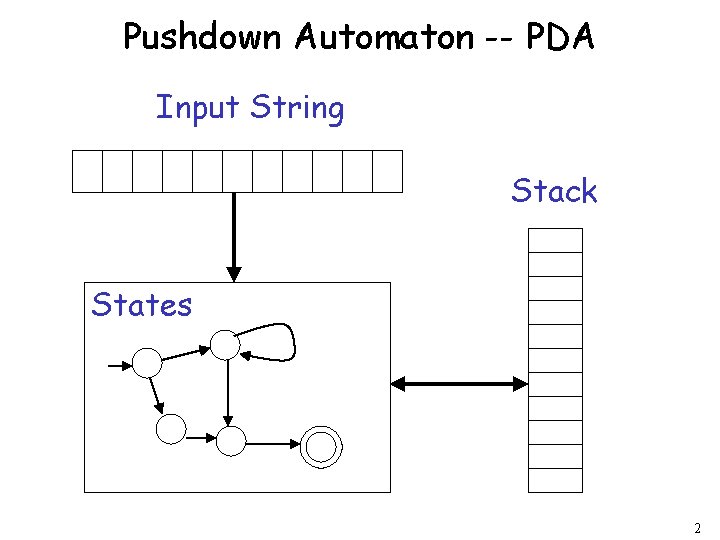
Pushdown Automaton -- PDA Input String Stack States 2

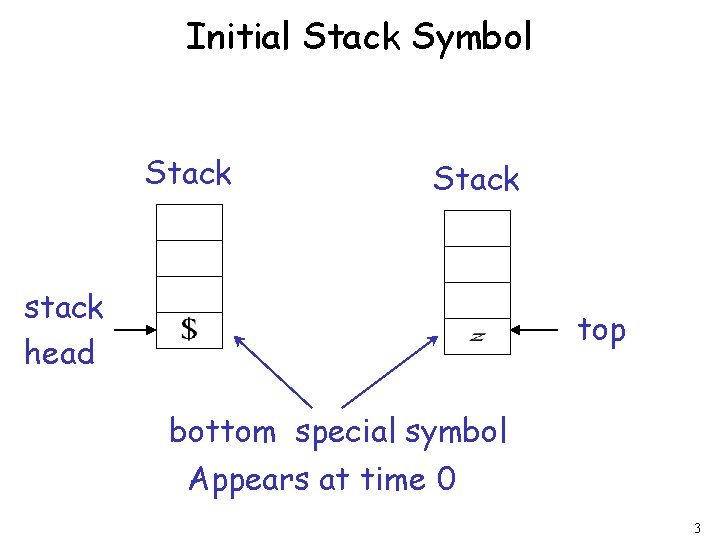
Initial Stack Symbol Stack stack head top bottom special symbol Appears at time 0 3

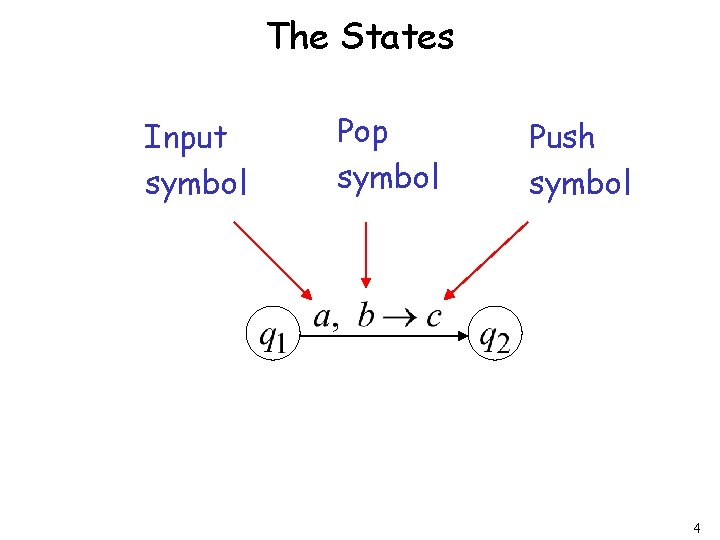
The States Input symbol Pop symbol Push symbol 4

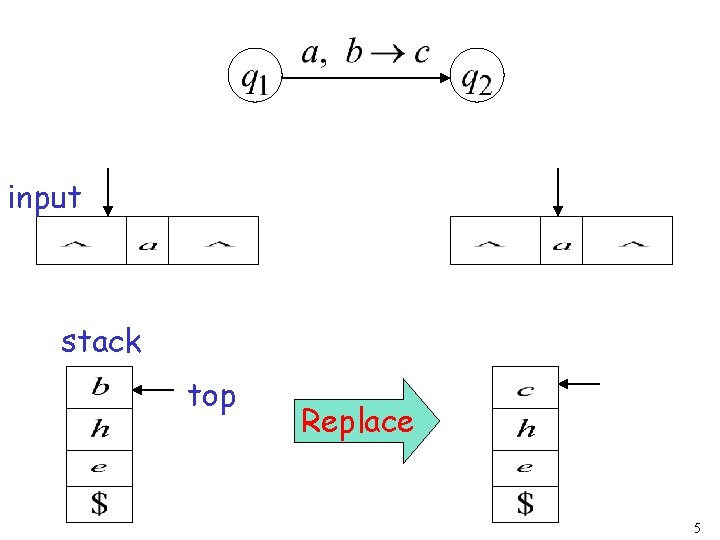
input stack top Replace 5

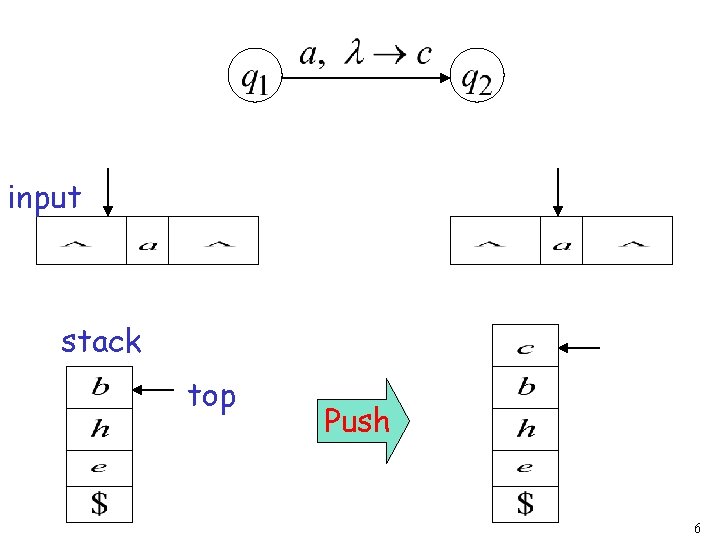
input stack top Push 6

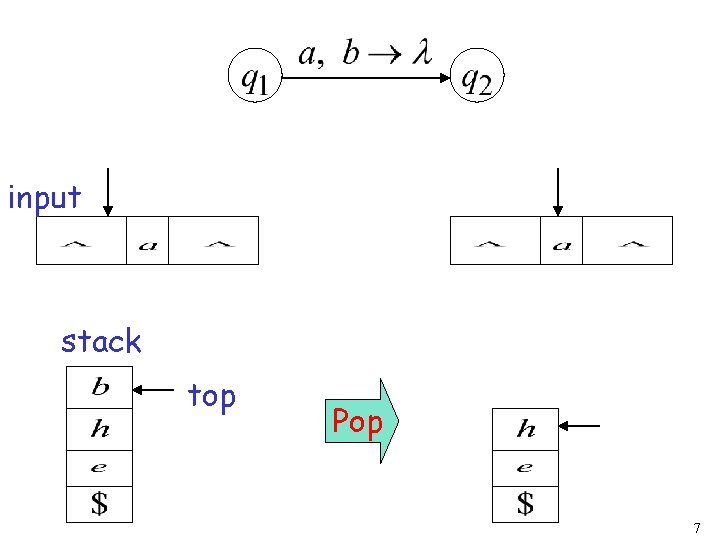
input stack top Pop 7

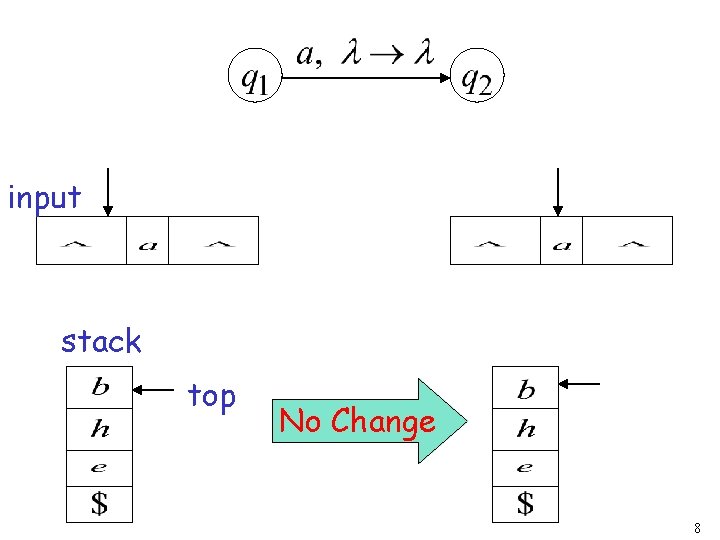
input stack top No Change 8

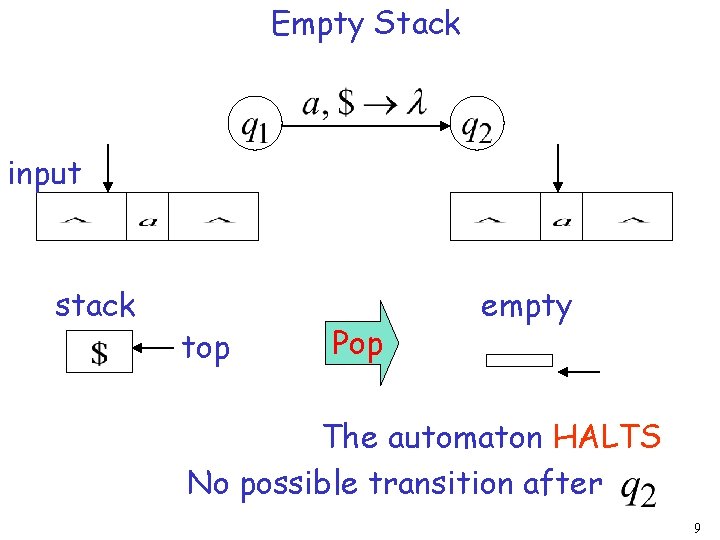
Empty Stack input stack top Pop empty The automaton HALTS No possible transition after 9

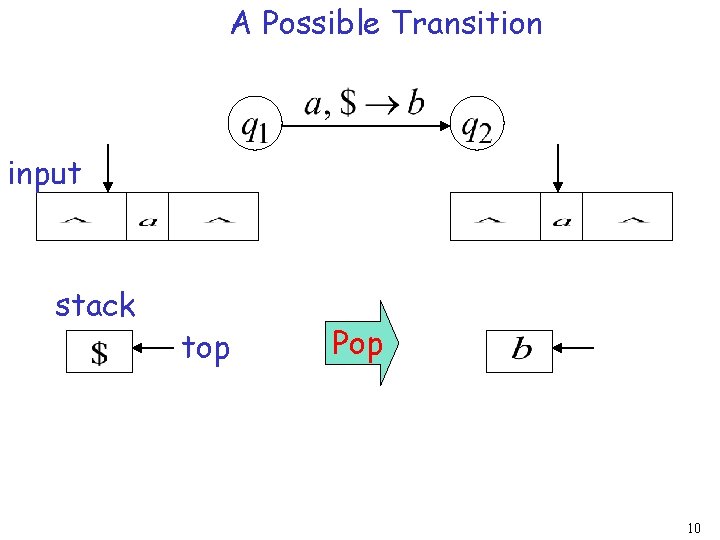
A Possible Transition input stack top Pop 10

Non-Determinism PDAs are non-deterministic Allowed non-deterministic transitions 11

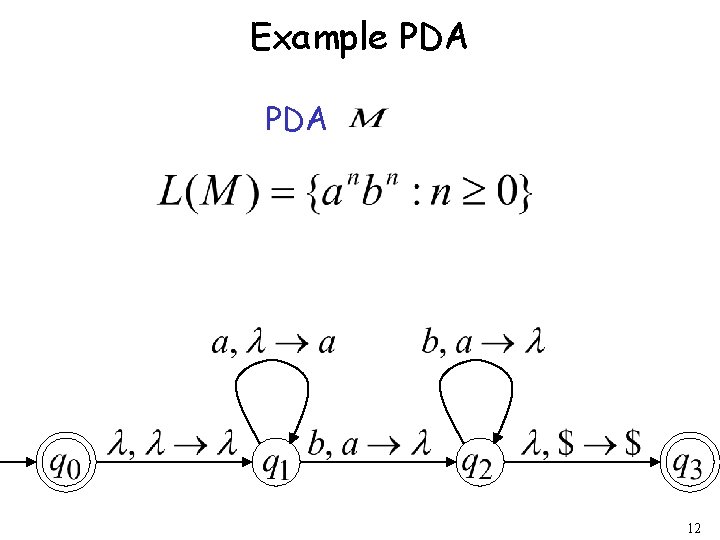
Example PDA 12

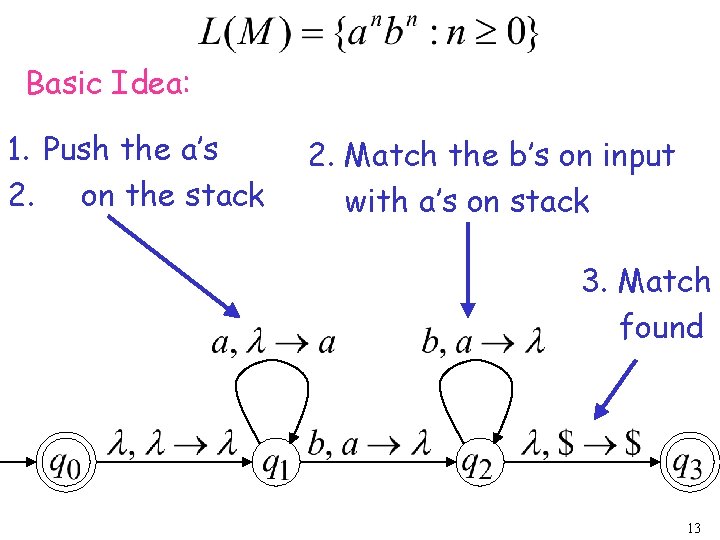
Basic Idea: 1. Push the a’s 2. on the stack 2. Match the b’s on input with a’s on stack 3. Match found 13

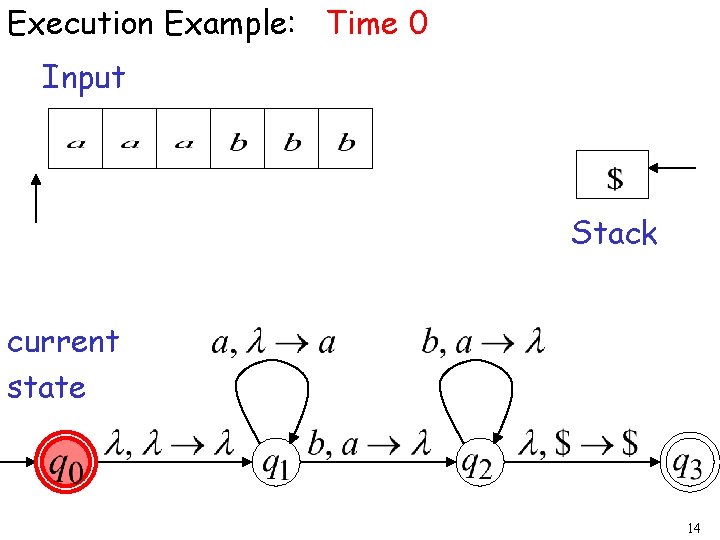
Execution Example: Time 0 Input Stack current state 14

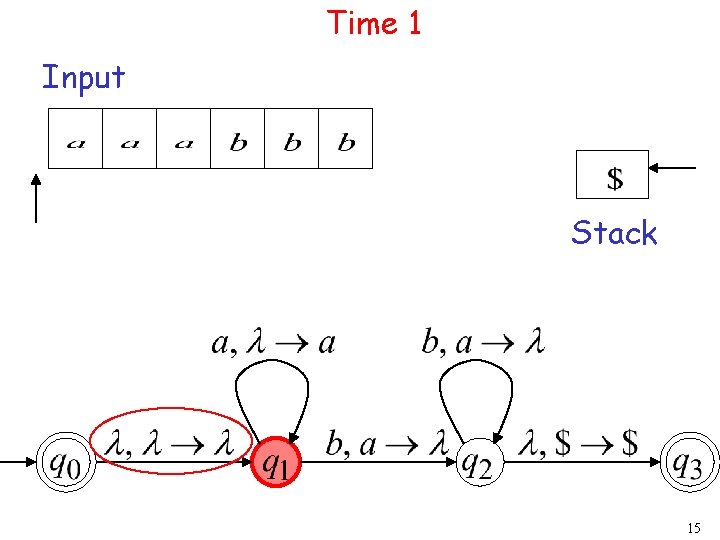
Time 1 Input Stack 15

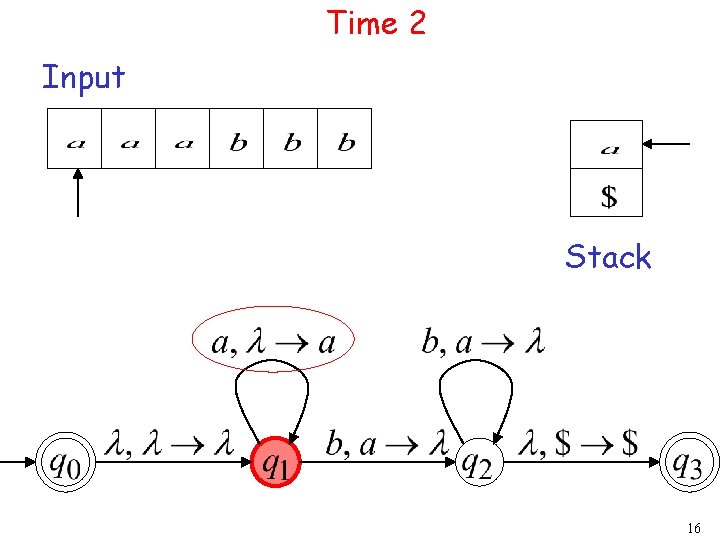
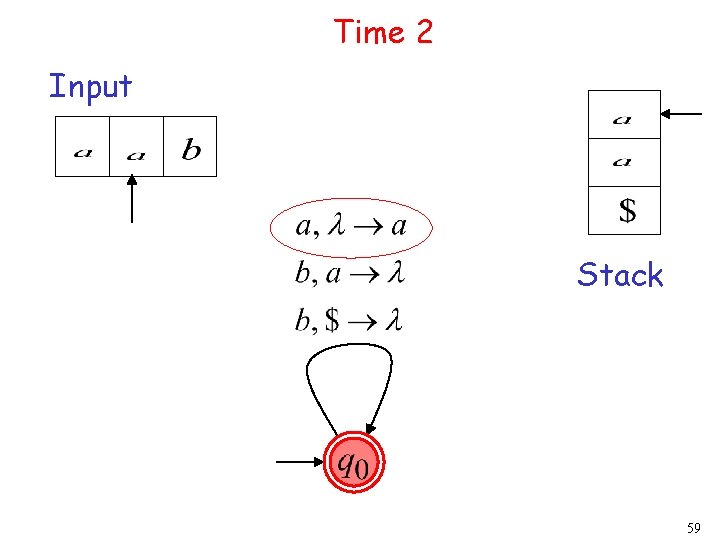
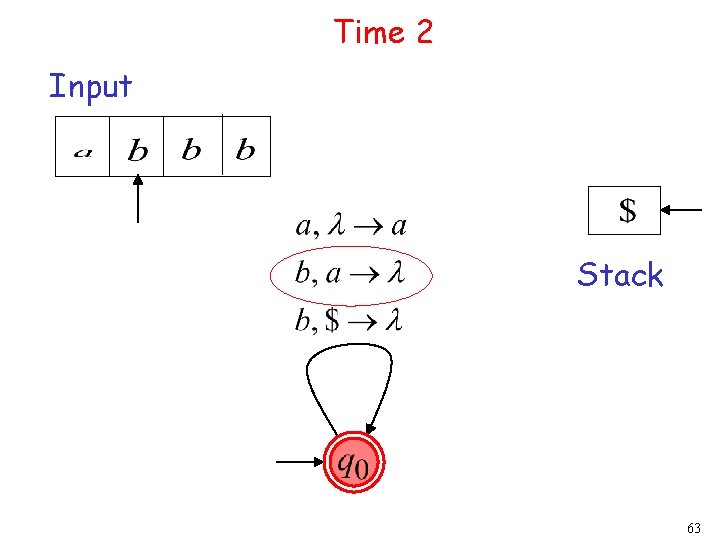
Time 2 Input Stack 16

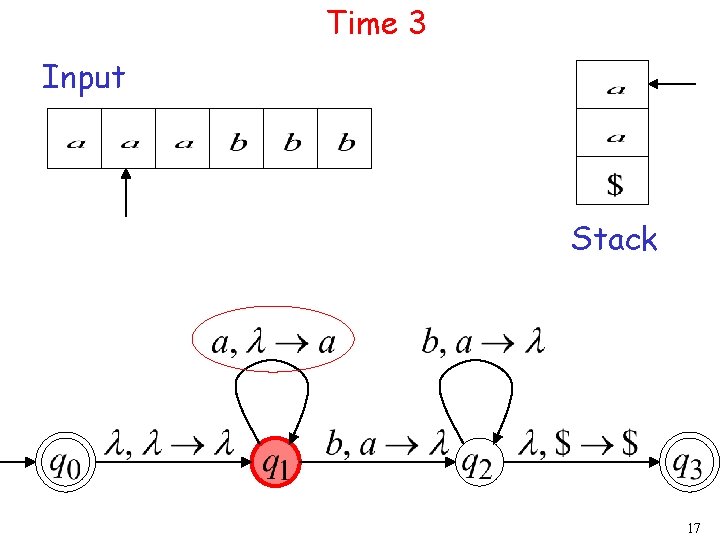
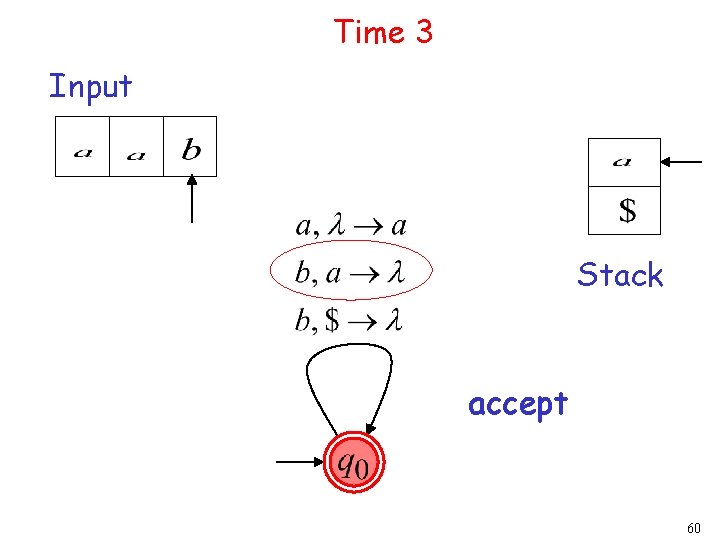
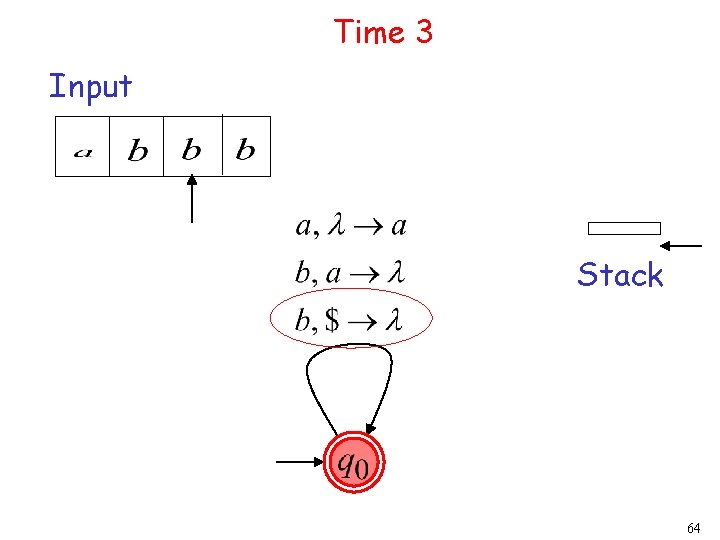
Time 3 Input Stack 17

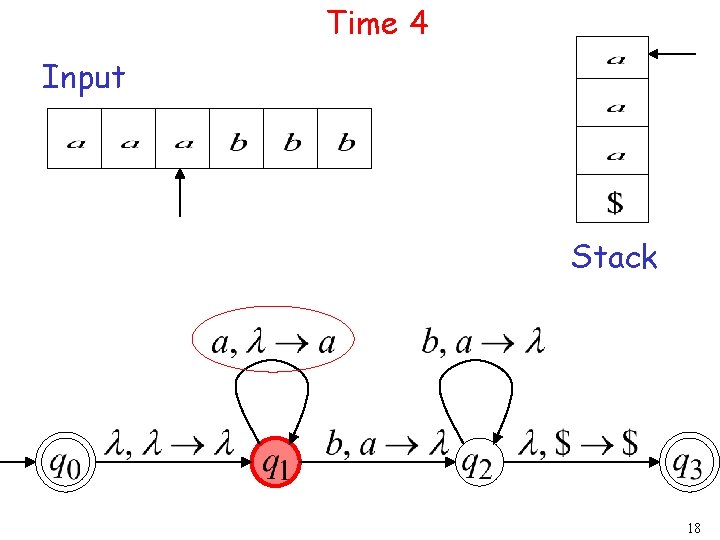
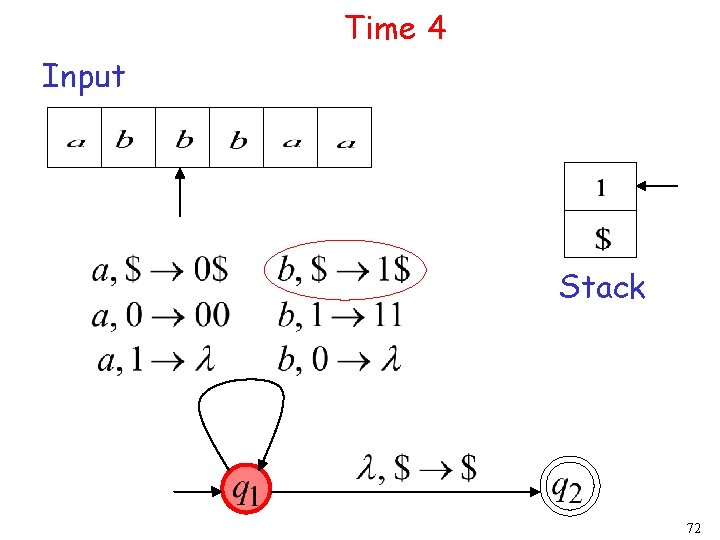
Time 4 Input Stack 18

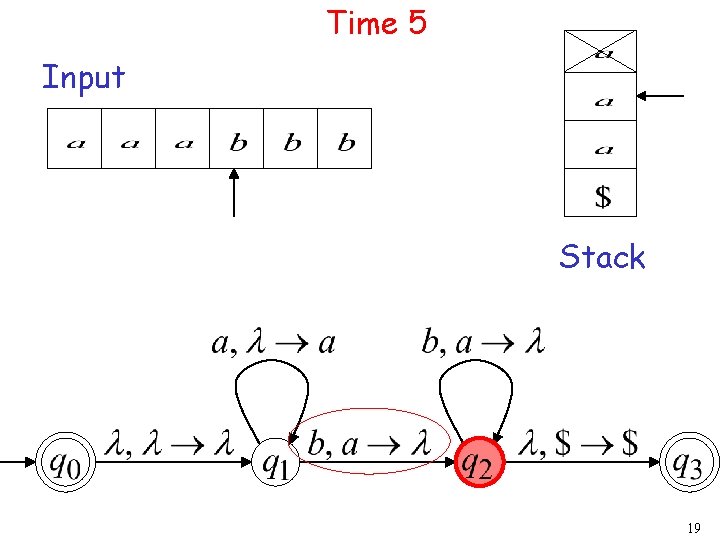
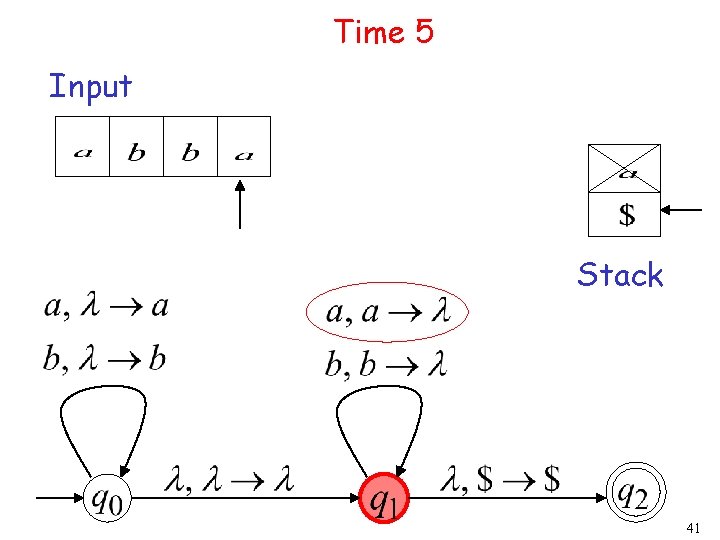
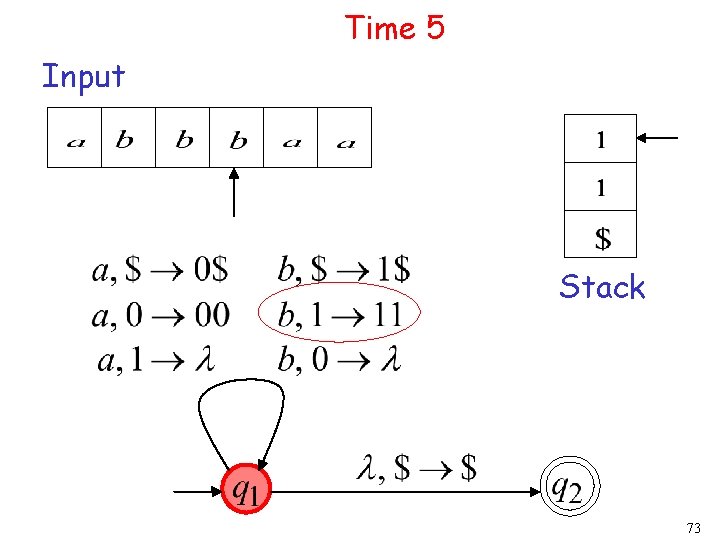
Time 5 Input Stack 19

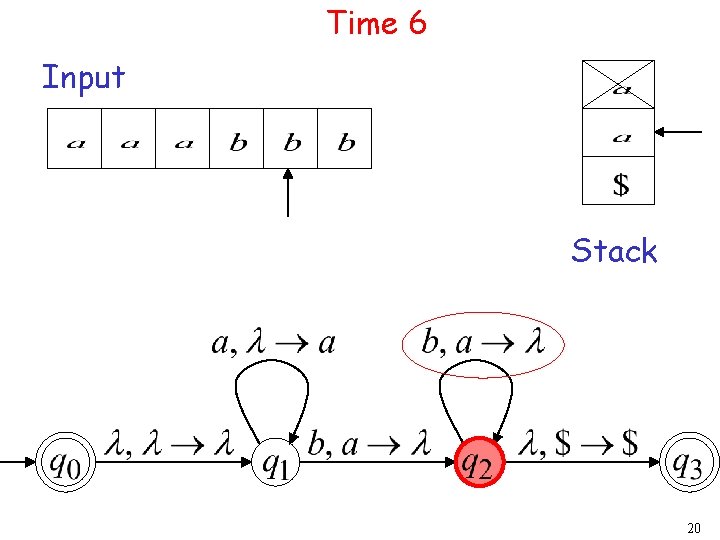
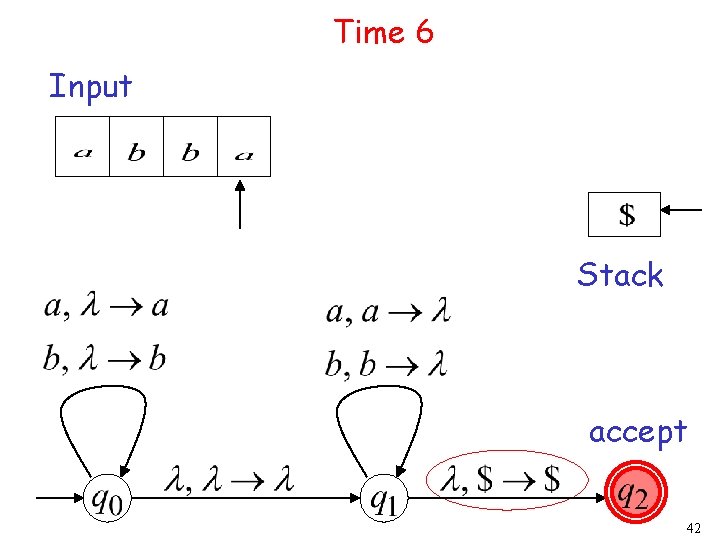
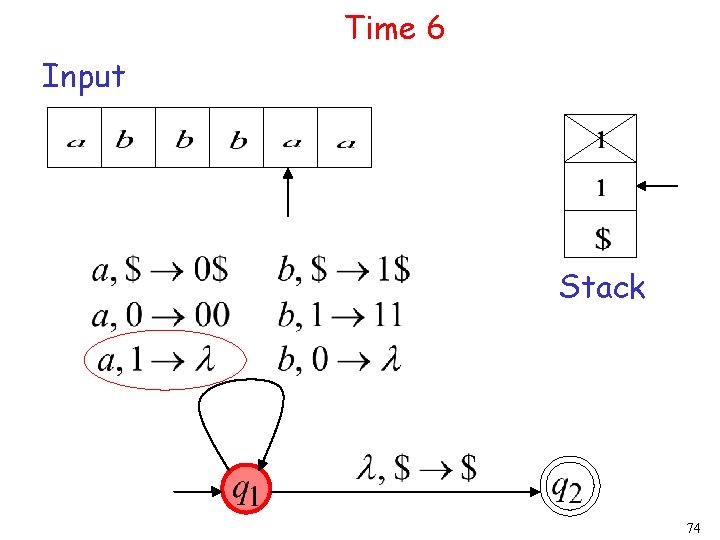
Time 6 Input Stack 20

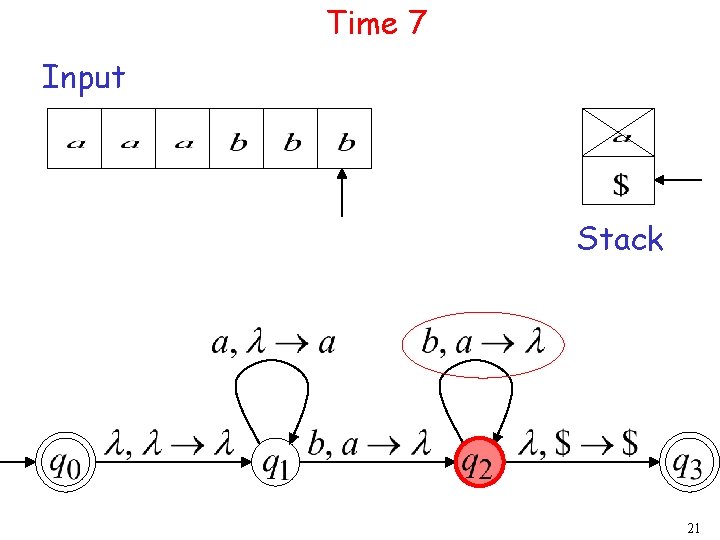
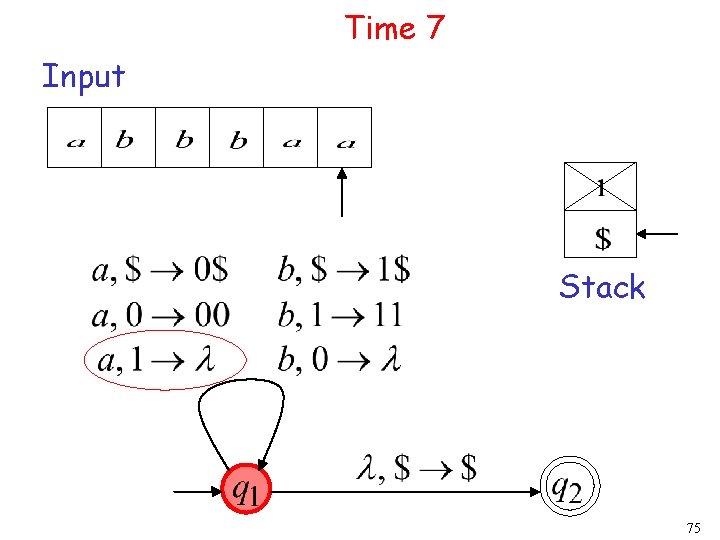
Time 7 Input Stack 21

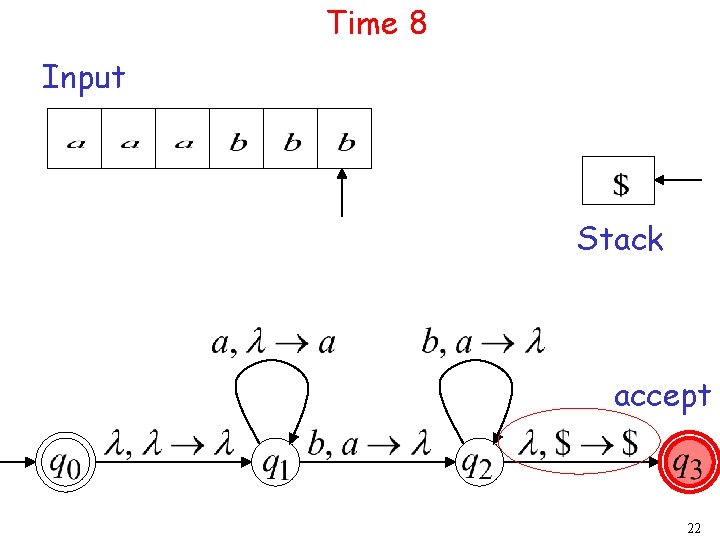
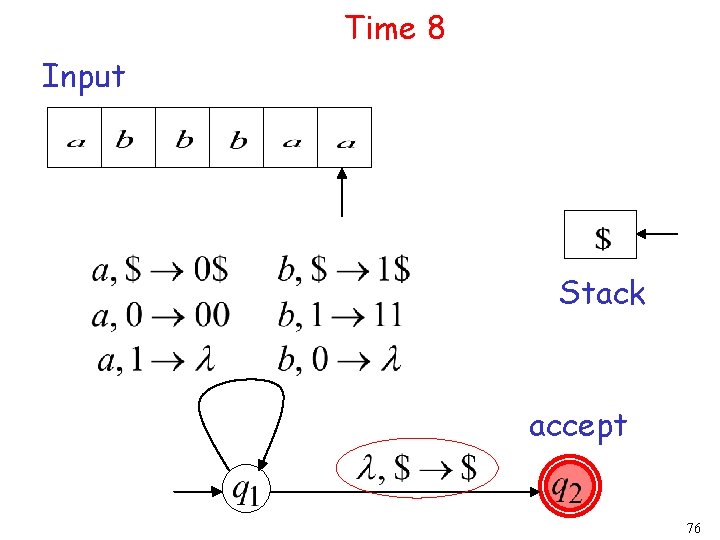
Time 8 Input Stack accept 22

A string is accepted if there is a computation such that: All the input is consumed AND The last state is an accepting state At the end of the computation, we do not care about the stack contents (the stack can be empty at the last state) 23

The input string is accepted by the PDA: 24

In general, is the language accepted by the PDA: 25

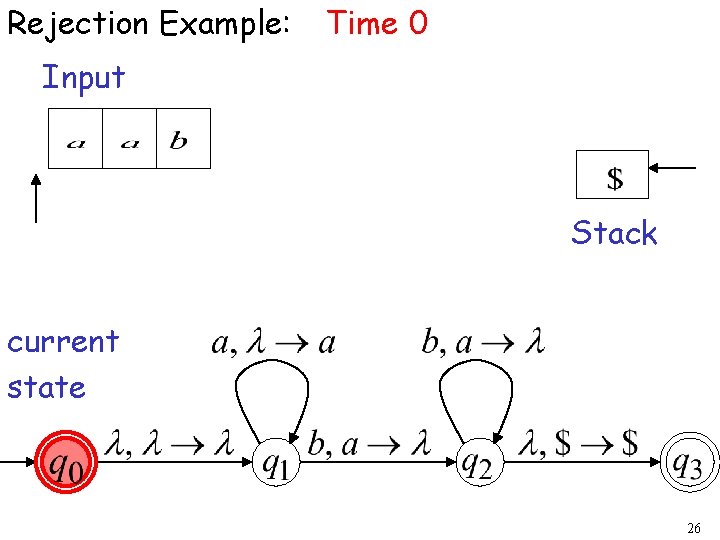
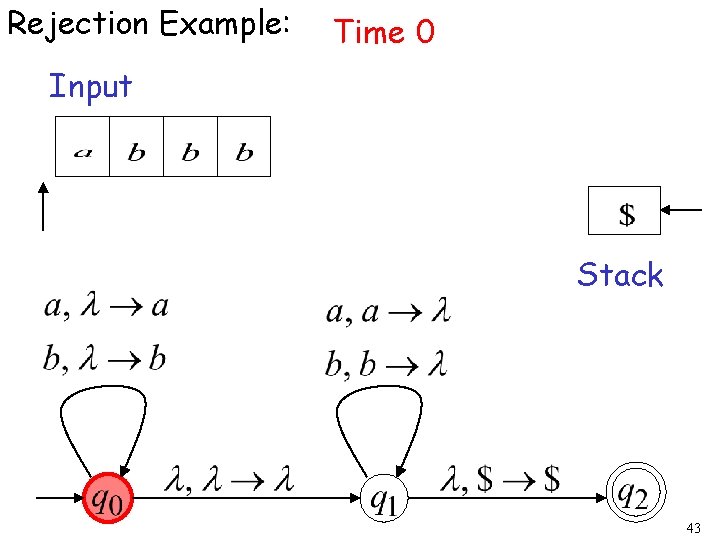
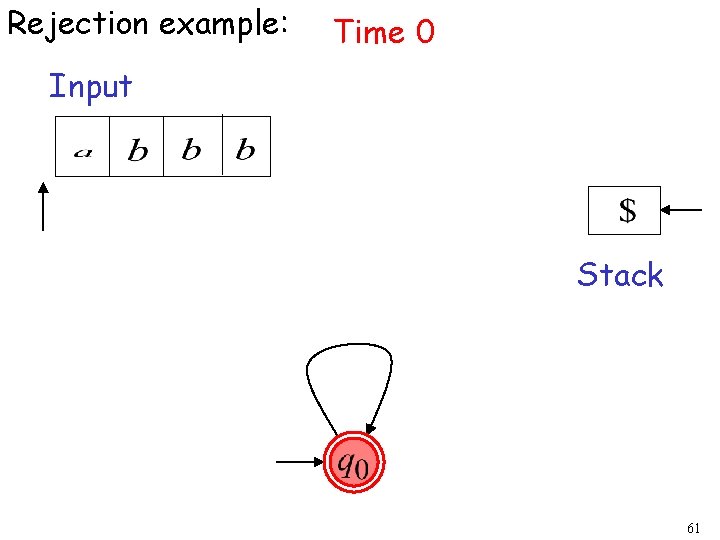
Rejection Example: Time 0 Input Stack current state 26

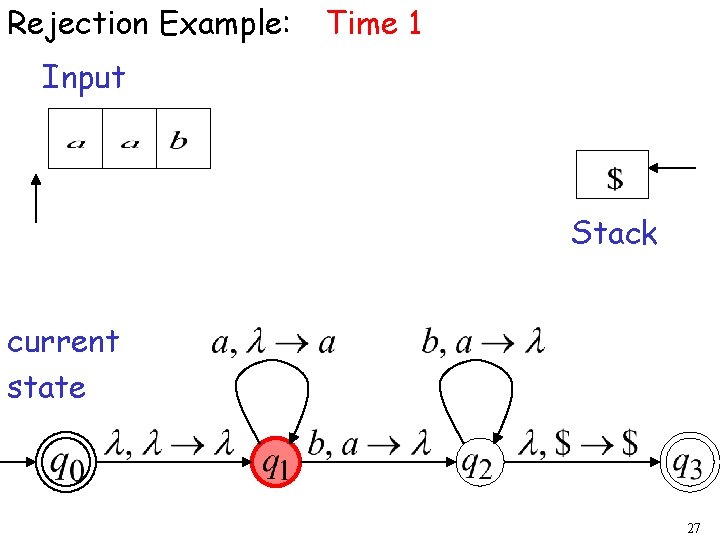
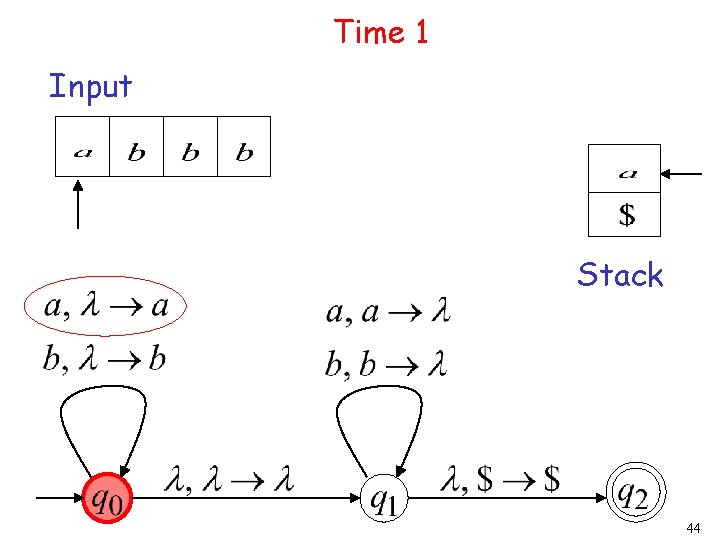
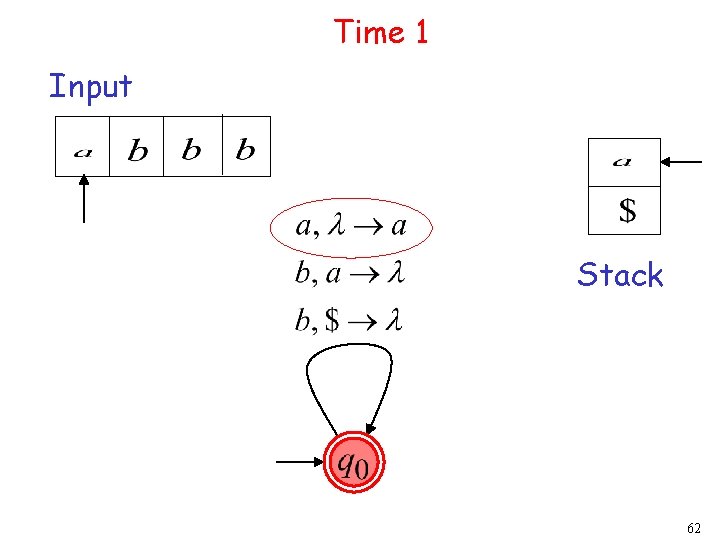
Rejection Example: Time 1 Input Stack current state 27

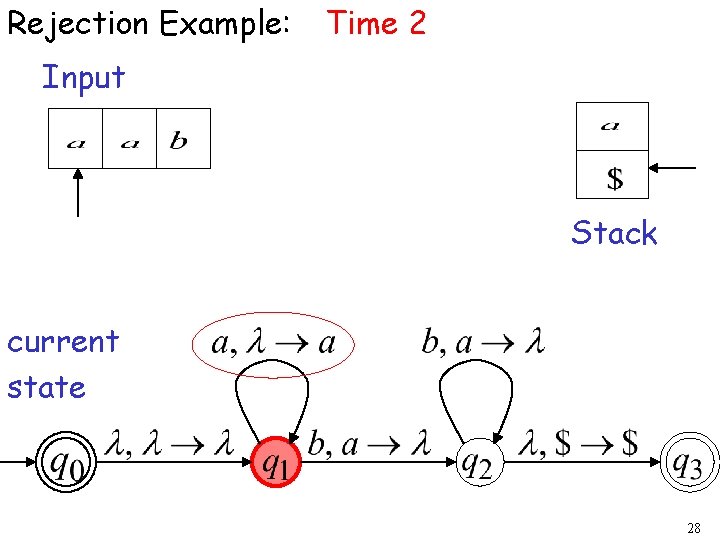
Rejection Example: Time 2 Input Stack current state 28

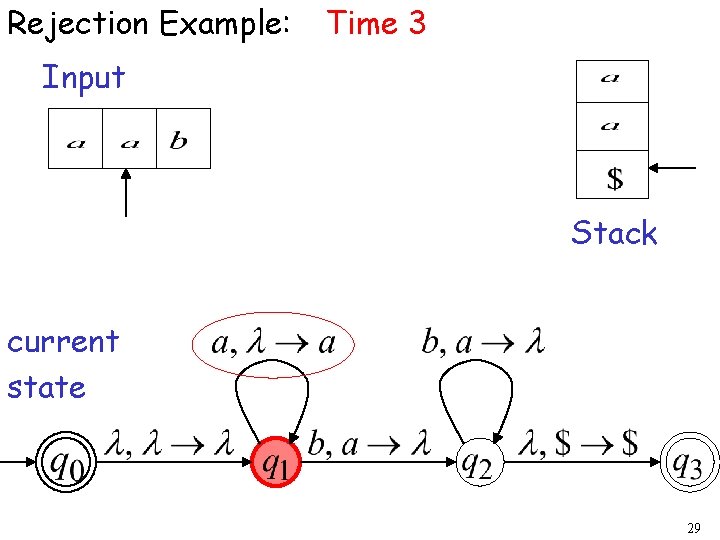
Rejection Example: Time 3 Input Stack current state 29

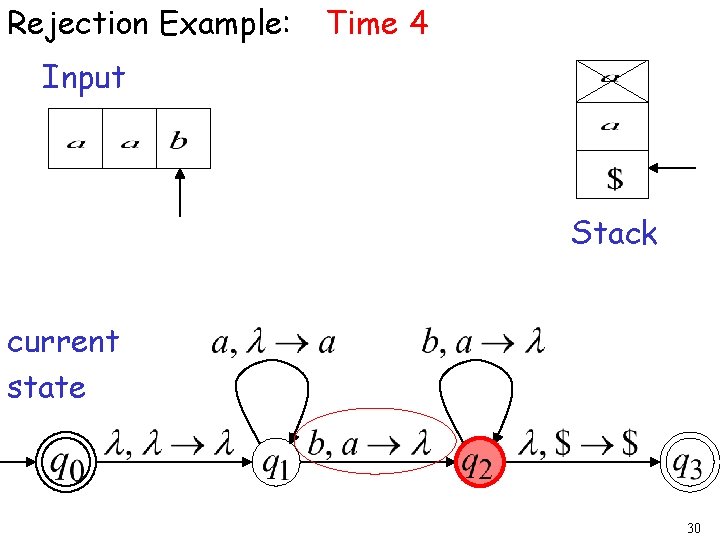
Rejection Example: Time 4 Input Stack current state 30

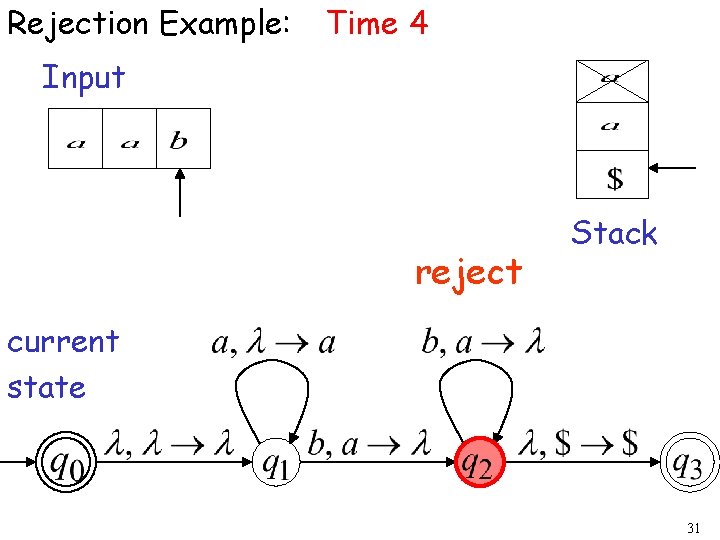
Rejection Example: Time 4 Input reject Stack current state 31

The input string is rejected by the PDA: 32

A string is rejected if there is no computation such that: All the input is consumed AND The last state is an accept state At the end of the computation, we do not care about the stack contents 33

Another PDA example PDA 34

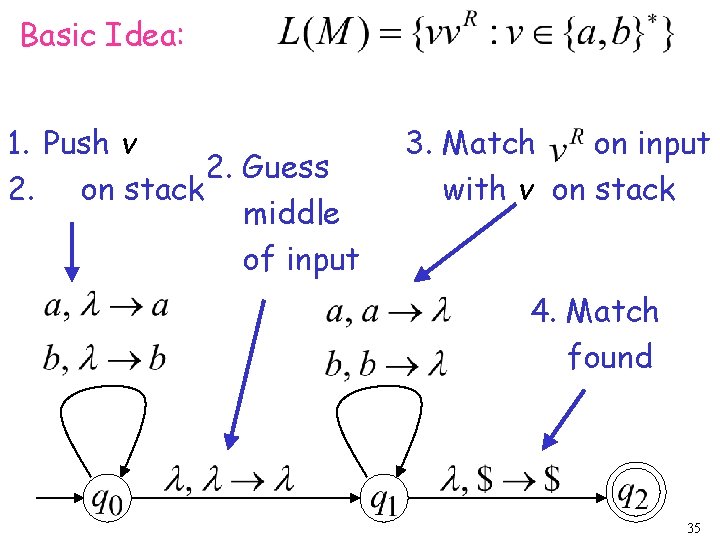
Basic Idea: 1. Push v 2. Guess 2. on stack middle of input 3. Match on input with v on stack 4. Match found 35

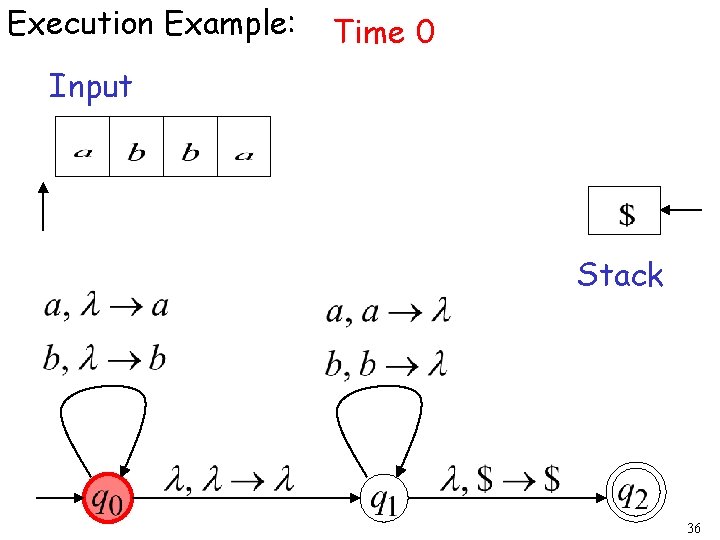
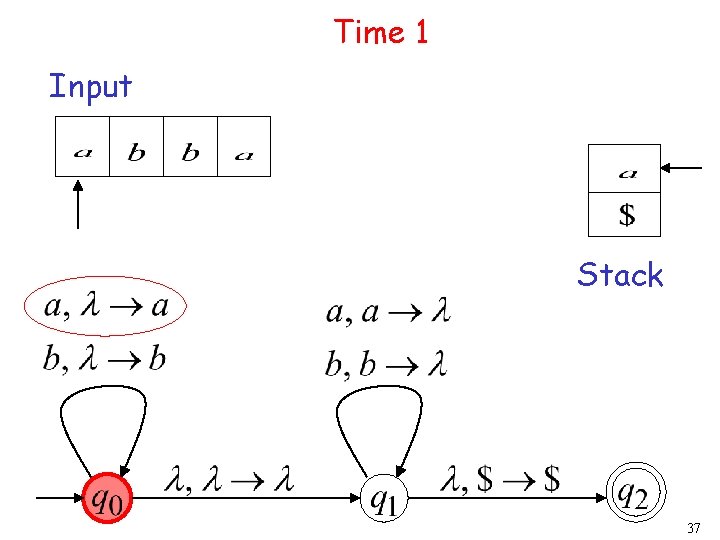
Execution Example: Time 0 Input Stack 36

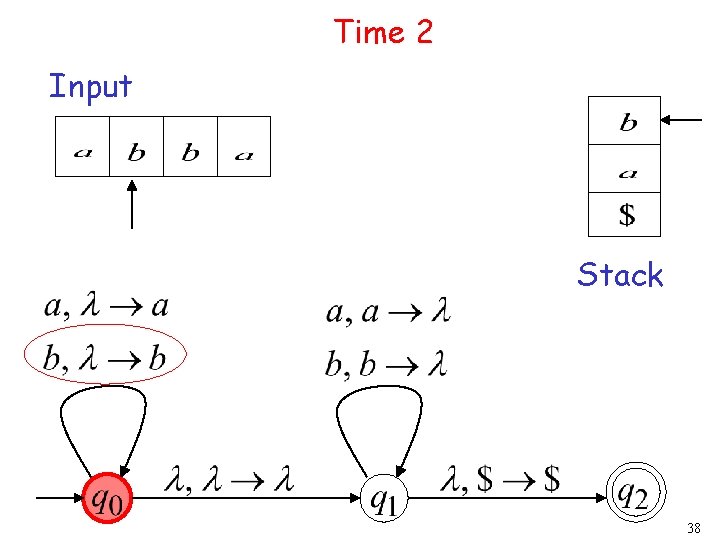
Time 1 Input Stack 37

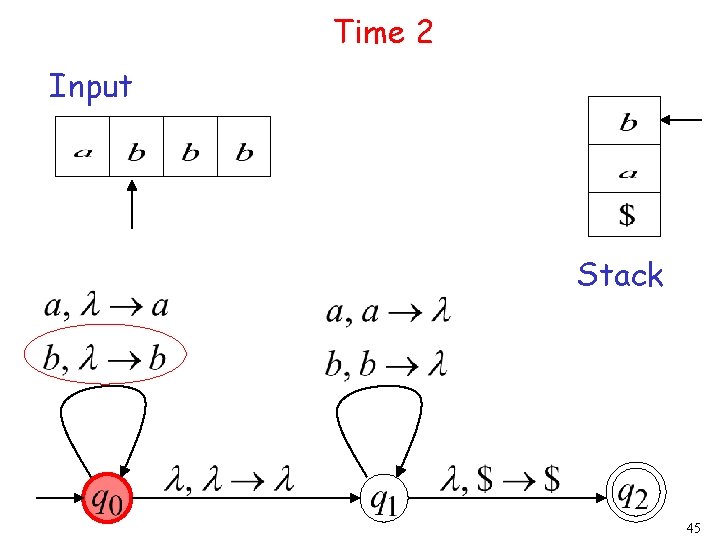
Time 2 Input Stack 38

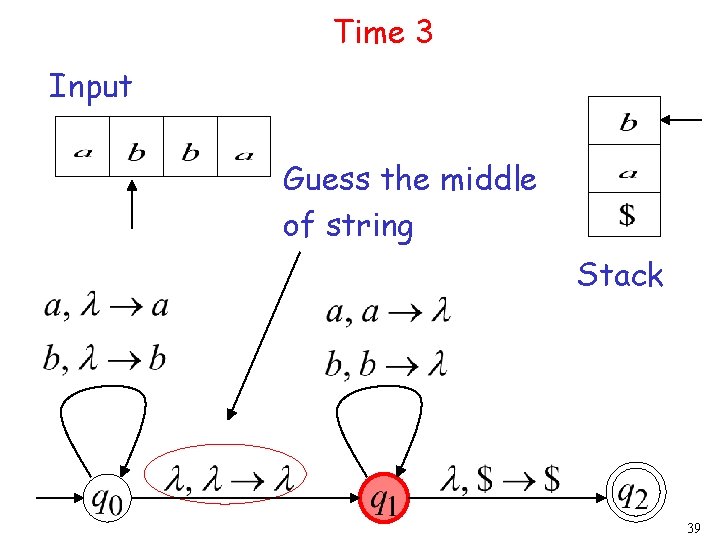
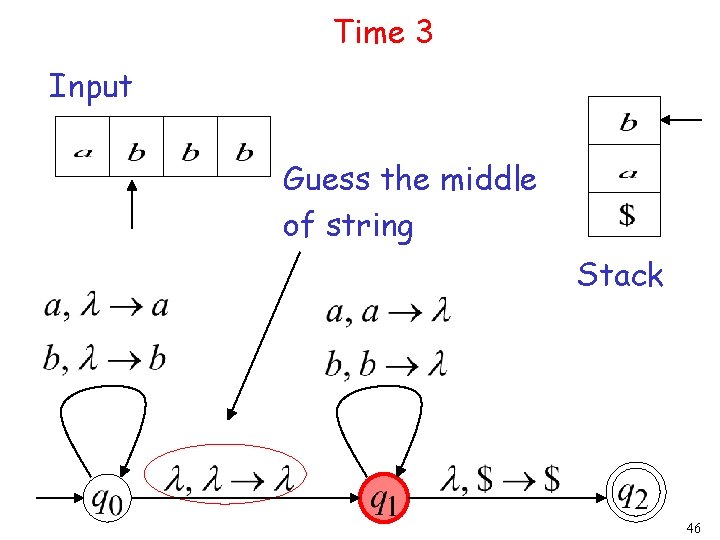
Time 3 Input Guess the middle of string Stack 39

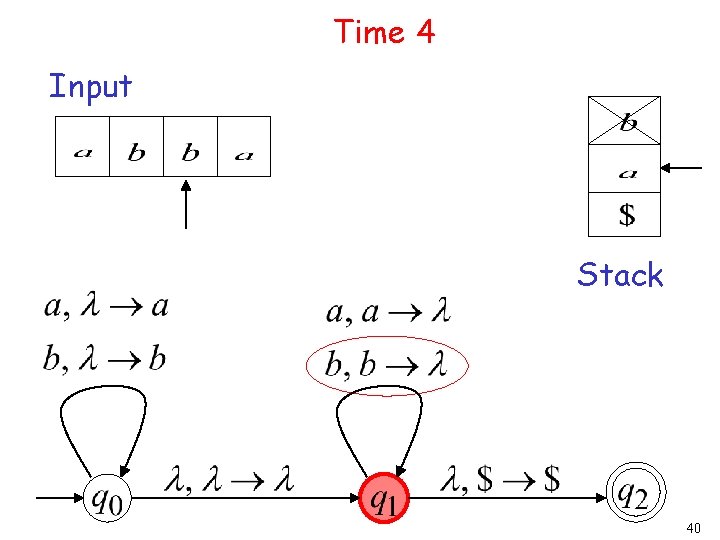
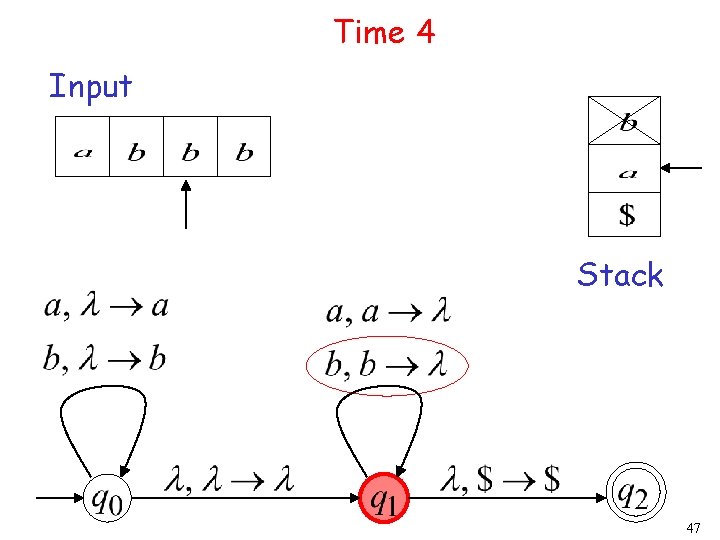
Time 4 Input Stack 40

Time 5 Input Stack 41

Time 6 Input Stack accept 42

Rejection Example: Time 0 Input Stack 43

Time 1 Input Stack 44

Time 2 Input Stack 45

Time 3 Input Guess the middle of string Stack 46

Time 4 Input Stack 47

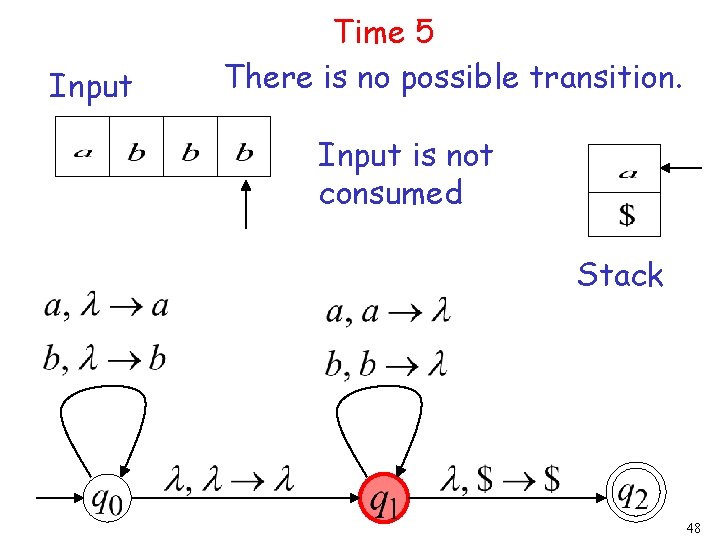
Input Time 5 There is no possible transition. Input is not consumed Stack 48

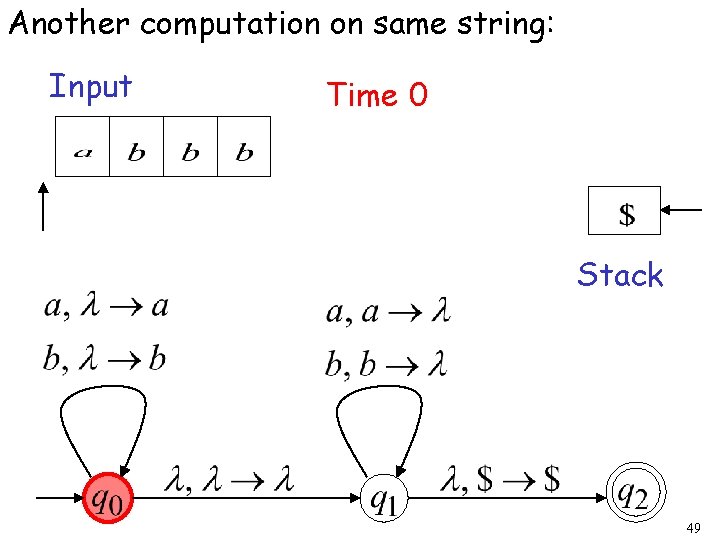
Another computation on same string: Input Time 0 Stack 49

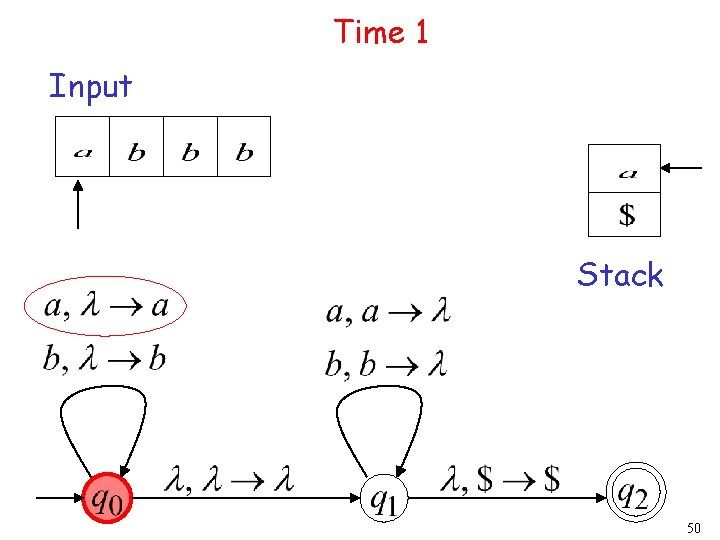
Time 1 Input Stack 50

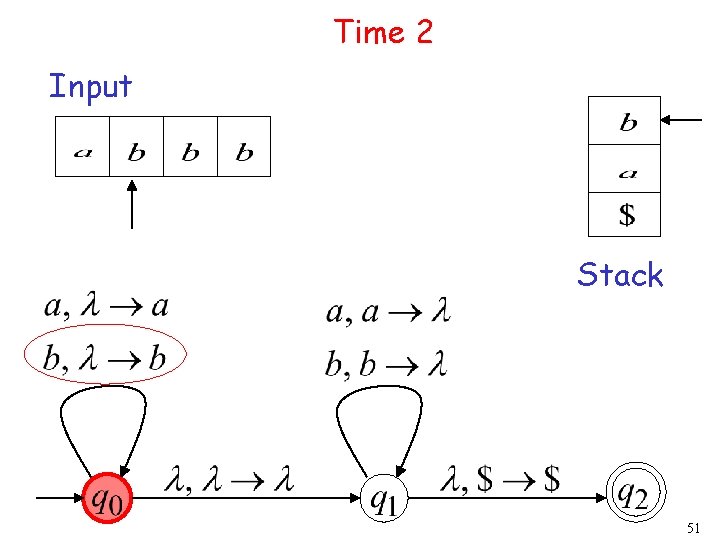
Time 2 Input Stack 51

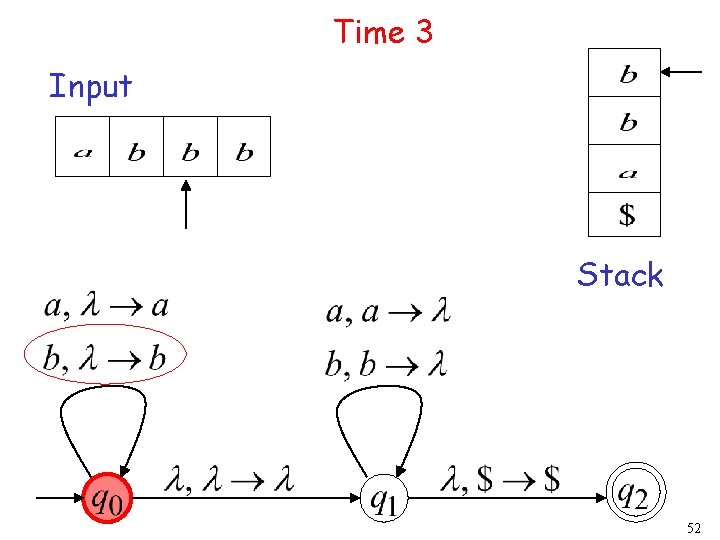
Time 3 Input Stack 52

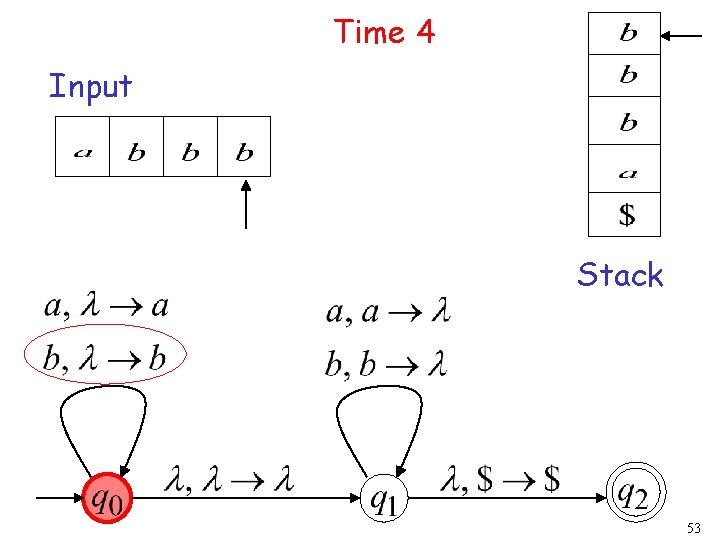
Time 4 Input Stack 53

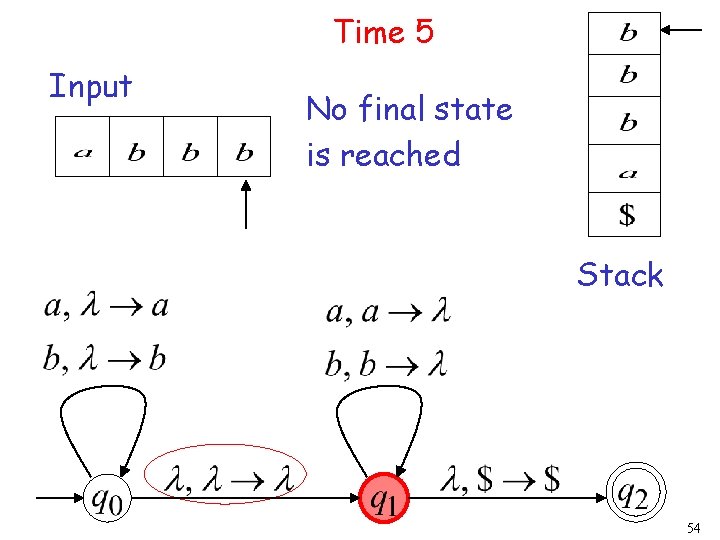
Time 5 Input No final state is reached Stack 54

There is no computation that accepts string 55

Another PDA example PDA 56

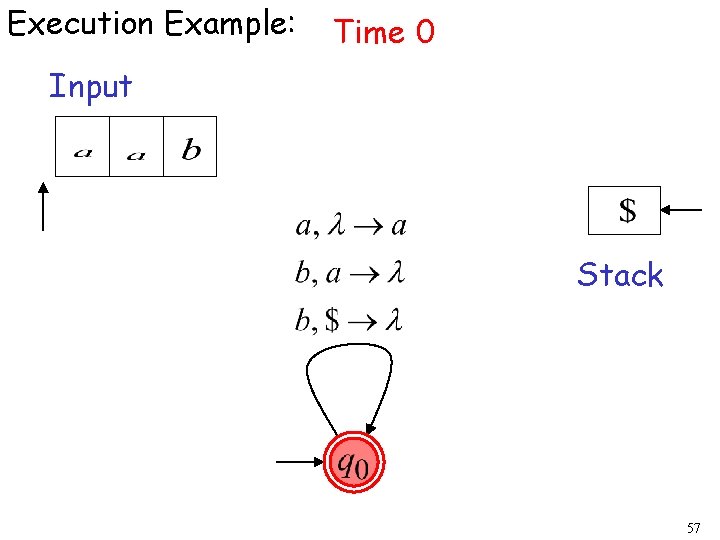
Execution Example: Time 0 Input Stack 57

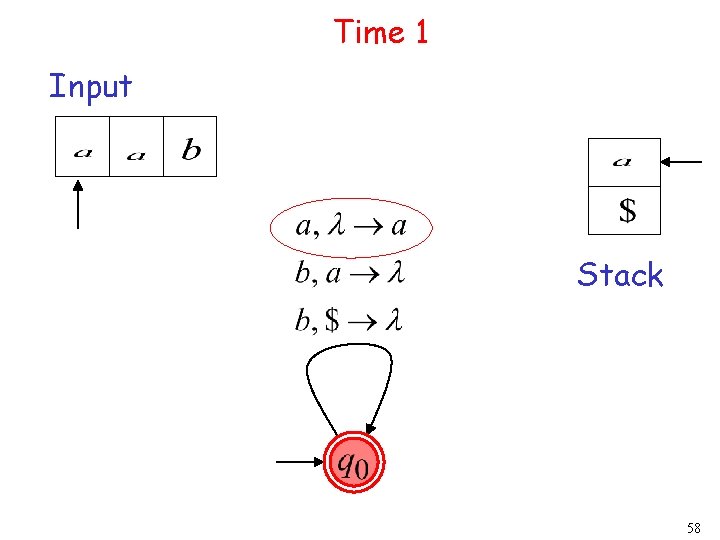
Time 1 Input Stack 58

Time 2 Input Stack 59

Time 3 Input Stack accept 60

Rejection example: Time 0 Input Stack 61

Time 1 Input Stack 62

Time 2 Input Stack 63

Time 3 Input Stack 64

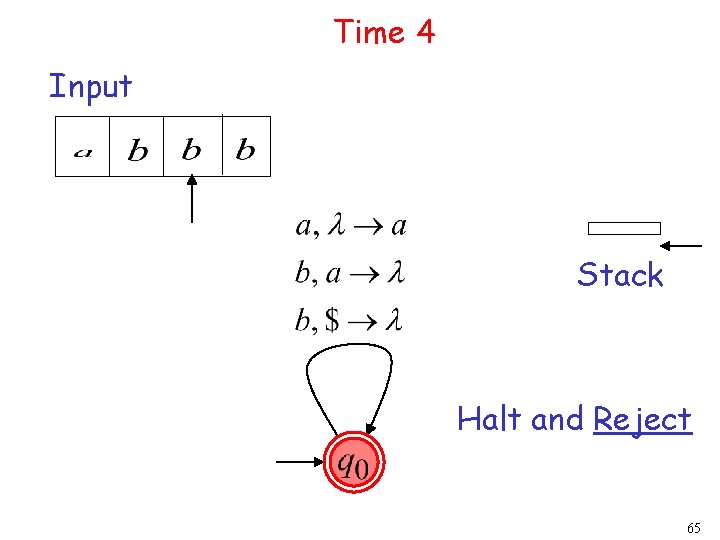
Time 4 Input Stack Halt and Reject 65

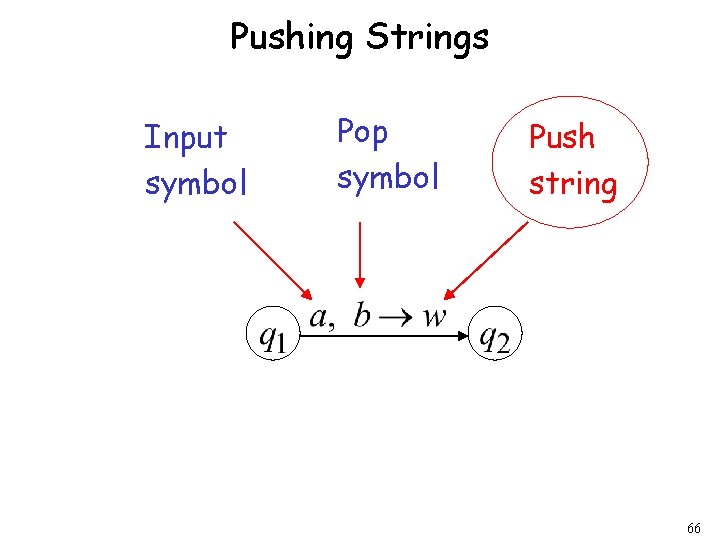
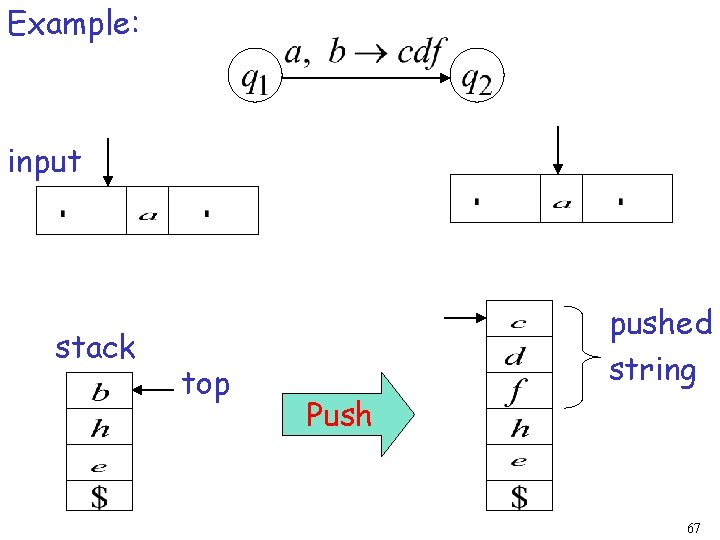
Pushing Strings Input symbol Pop symbol Push string 66

Example: input stack top pushed string Push 67

Another PDA example PDA 68

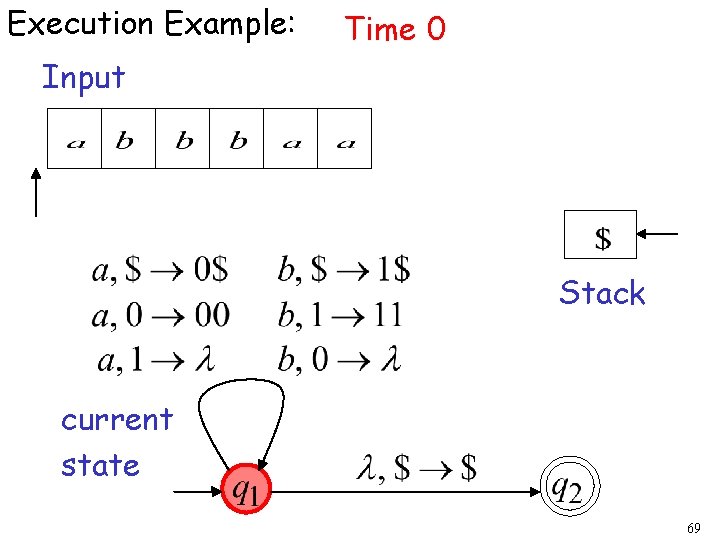
Execution Example: Time 0 Input Stack current state 69

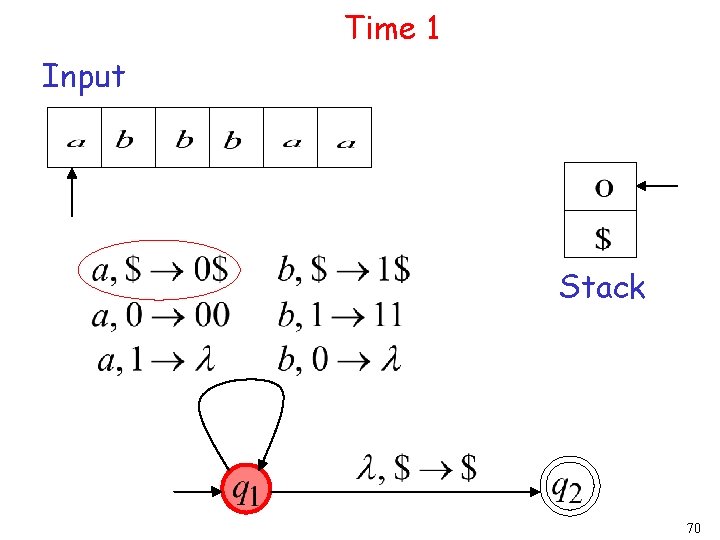
Time 1 Input Stack 70

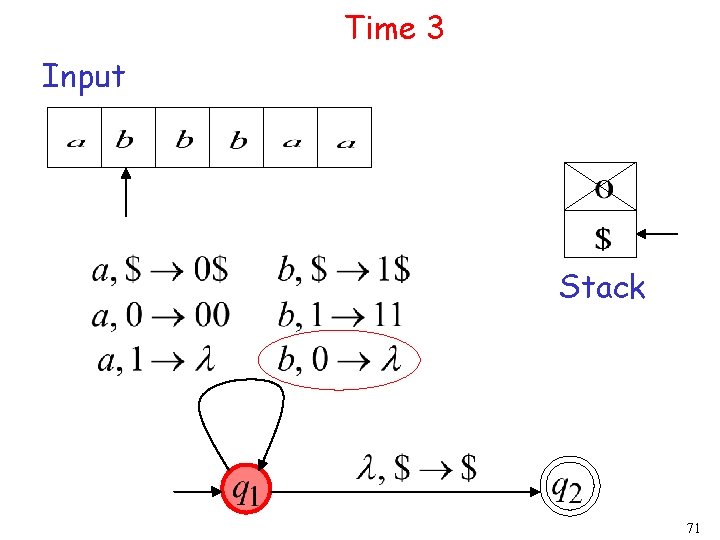
Time 3 Input Stack 71

Time 4 Input Stack 72

Time 5 Input Stack 73

Time 6 Input Stack 74

Time 7 Input Stack 75

Time 8 Input Stack accept 76

Formalities for PDAs 77

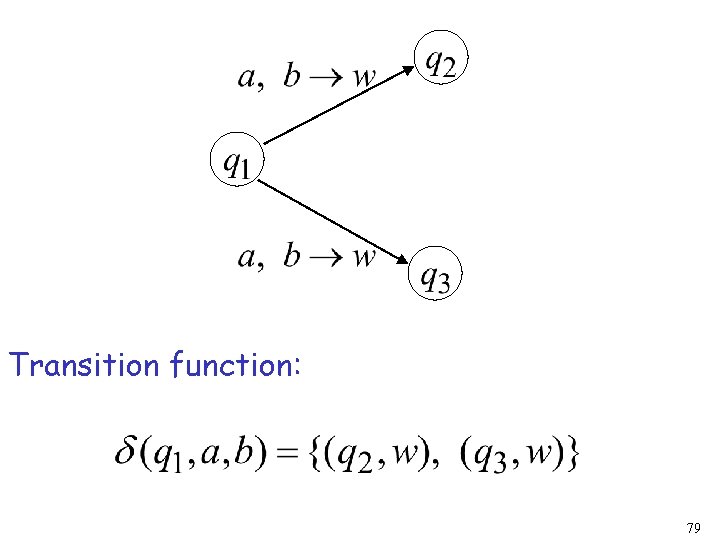
Transition function: 78

Transition function: 79

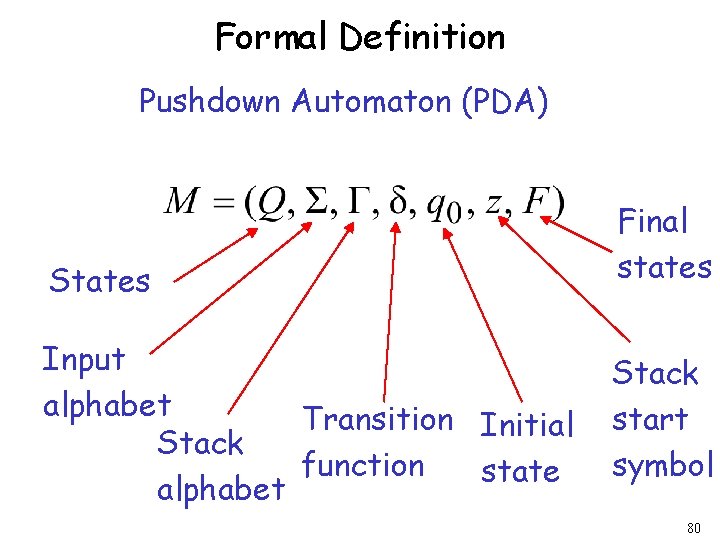
Formal Definition Pushdown Automaton (PDA) States Input alphabet Transition Initial Stack function state alphabet Final states Stack start symbol 80

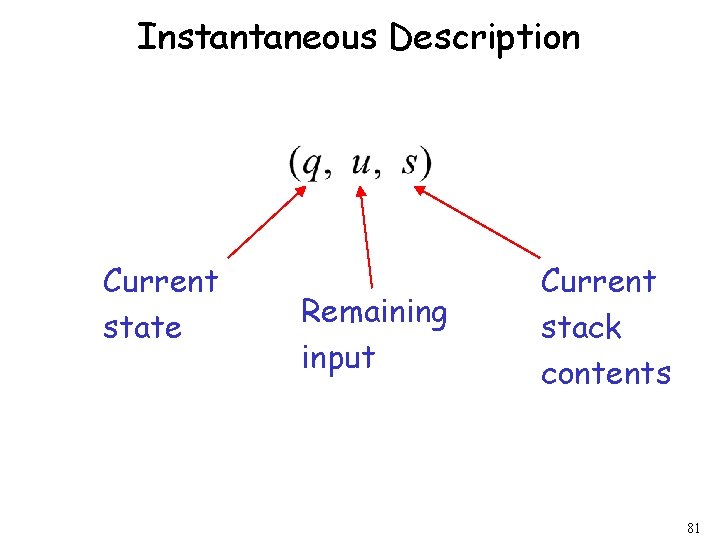
Instantaneous Description Current state Remaining input Current stack contents 81

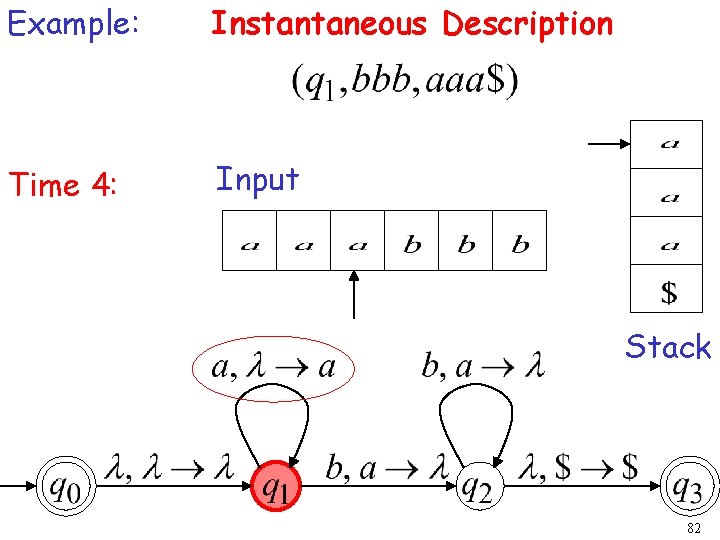
Example: Instantaneous Description Time 4: Input Stack 82

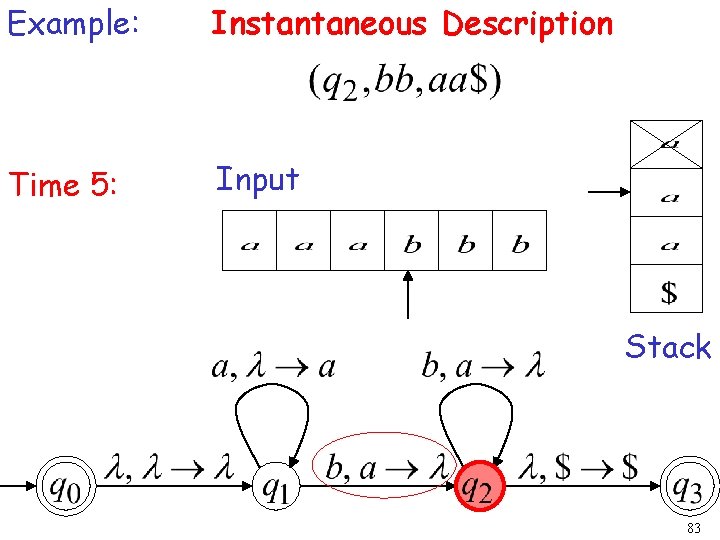
Example: Instantaneous Description Time 5: Input Stack 83

We write: Time 4 Time 5 84

A computation: 85

For convenience we write: 86

Formal Definition Language of PDA Initial state : Final state 87

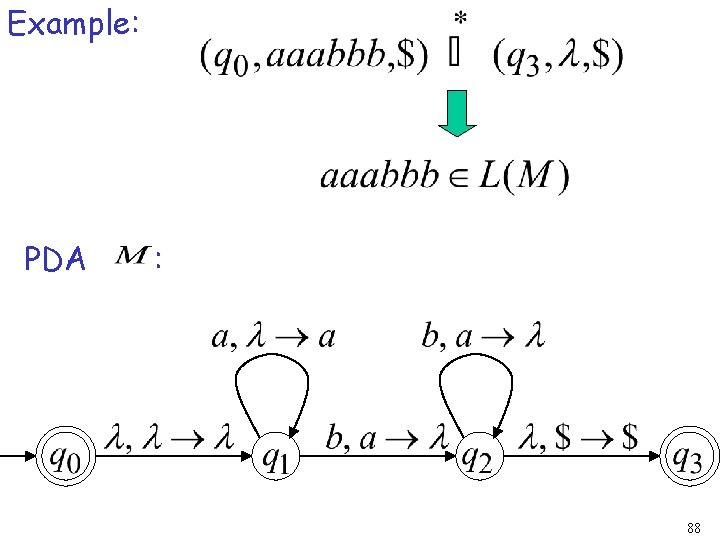
Example: PDA : 88

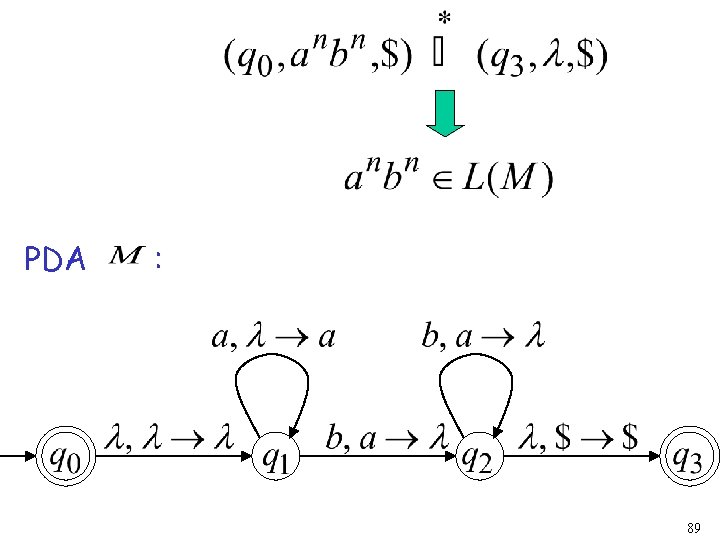
PDA : 89

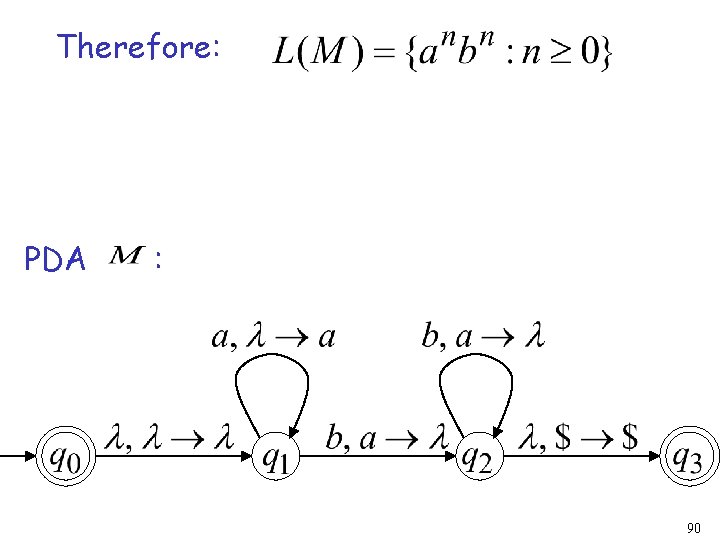
Therefore: PDA : 90