Pushdown Automata PDA Reading Chapter 6 1 PDA

Pushdown Automata (PDA) Reading: Chapter 6 1

PDA - the automata for CFLs n What is? n n n FA to Reg Lang, PDA is to CFL PDA == [ -NFA + “a stack” ] Why a stack? Input string -NFA Accept/reject A stack filled with “stack symbols” 2

Pushdown Automata Definition n A PDA P : = ( Q, ∑, , δ, q 0, Z 0, F ): n n n n Q: ∑: : δ: q 0: Z 0: F: states of the -NFA input alphabet stack symbols transition function start state Initial stack top symbol Final/accepting states 3

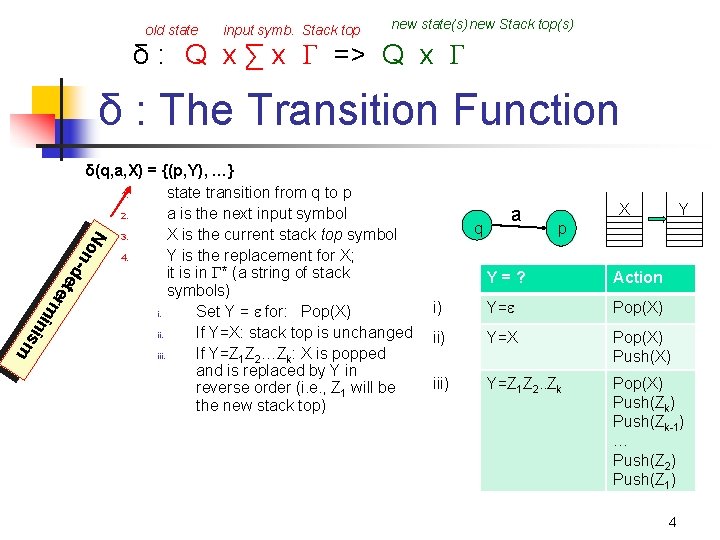
old state input symb. Stack top new state(s) new Stack top(s) δ : Q x ∑ x => Q x δ : The Transition Function q a X Y p i n i sm m e t e r d on - N δ(q, a, X) = {(p, Y), …} 1. state transition from q to p 2. a is the next input symbol 3. X is the current stack top symbol 4. Y is the replacement for X; it is in * (a string of stack symbols) i. Set Y = for: Pop(X) ii. If Y=X: stack top is unchanged iii. If Y=Z 1 Z 2…Zk: X is popped and is replaced by Y in reverse order (i. e. , Z 1 will be the new stack top) Y=? Action i) Y= Pop(X) ii) Y=X Pop(X) Push(X) iii) Y=Z 1 Z 2. . Zk Pop(X) Push(Zk-1) … Push(Z 2) Push(Z 1) 4

Example Let Lwwr = {ww. R | w is in (0+1)*} n CFG for Lwwr : S==> 0 S 0 | 1 S 1 | n PDA for Lwwr : n P : = ( Q, ∑, , δ, q 0, Z 0, F ) = ( {q 0, q 1, q 2}, {0, 1, Z 0}, δ, q 0, Z 0, {q 2}) 5

Initial state of the PDA: PDA for Lwwr 1. 2. 3. 4. 5. 6. δ(q 0, 0, Z 0)={(q 0, 0 Z 0)} δ(q 0, 1, Z 0)={(q 0, 1 Z 0)} δ(q 0, 0, 0)={(q 0, 00)} δ(q 0, 0, 1)={(q 0, 01)} δ(q 0, 1, 0)={(q 0, 10)} δ(q 0, 1, 1)={(q 0, 11)} Stack top q 0 Z 0 First symbol push on stack Grow the stack by pushing new symbols on top of old (w-part) δ(q 0, , 0)={(q 1, 0)} δ(q 0, , 1)={(q 1, 1)} δ(q 0, , Z 0)={(q 1, Z 0)} Switch to popping mode, nondeterministically (boundary between w and w. R) 11. δ(q 1, 0, 0)={(q 1, )} δ(q 1, 1, 1)={(q 1, )} Shrink the stack by popping matching symbols (w. R-part) 12. δ(q 1, , Z 0)={(q 2, Z 0)} Enter acceptance state 7. 8. 9. 10. 6

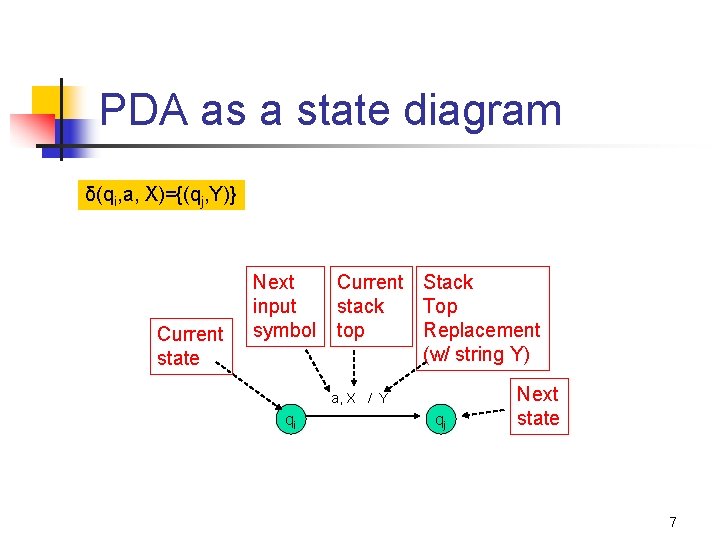
PDA as a state diagram δ(qi, a, X)={(qj, Y)} Current state Next input symbol Current Stack stack Top top Replacement (w/ string Y) a, X / Y qi qj Next state 7

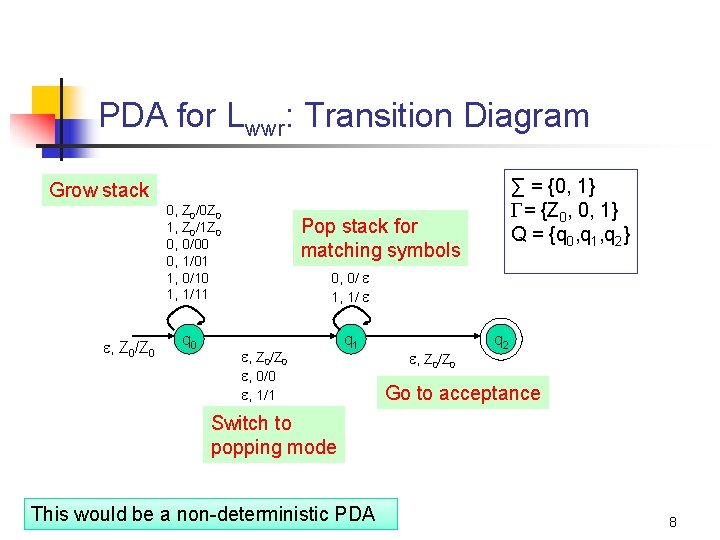
PDA for Lwwr: Transition Diagram ∑ = {0, 1} = {Z 0, 0, 1} Q = {q 0, q 1, q 2} Grow stack 0, Z 0/0 Z 0 1, Z 0/1 Z 0 0, 0/00 0, 1/01 1, 0/10 1, 1/11 , Z 0/Z 0 q 0 Pop stack for matching symbols 0, 0/ 1, 1/ , Z 0/Z 0 , 0/0 , 1/1 q 1 , Z 0/Z 0 q 2 Go to acceptance Switch to popping mode This would be a non-deterministic PDA 8

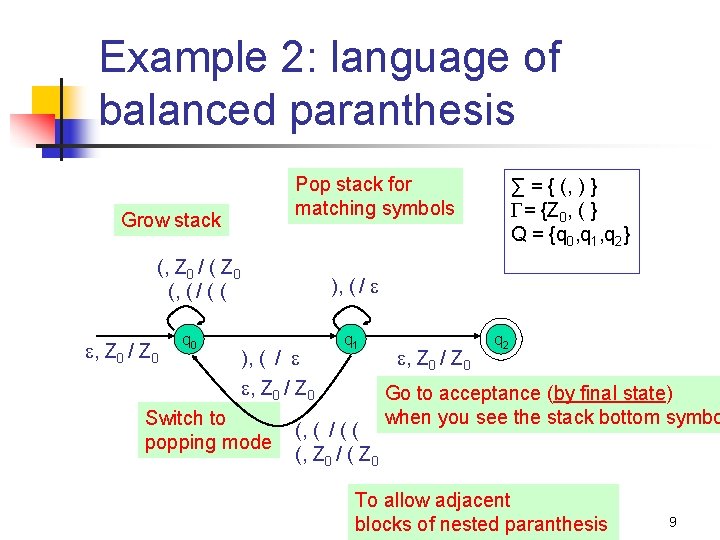
Example 2: language of balanced paranthesis Pop stack for matching symbols Grow stack (, Z 0 / ( Z 0 (, ( / ( ( , Z 0 / Z 0 q 0 ∑ = { (, ) } = {Z 0, ( } Q = {q 0, q 1, q 2} ), ( / , Z 0 / Z 0 Switch to popping mode q 1 (, ( / ( ( (, Z 0 / ( Z 0 , Z 0 / Z 0 q 2 Go to acceptance (by final state) when you see the stack bottom symbo To allow adjacent blocks of nested paranthesis 9

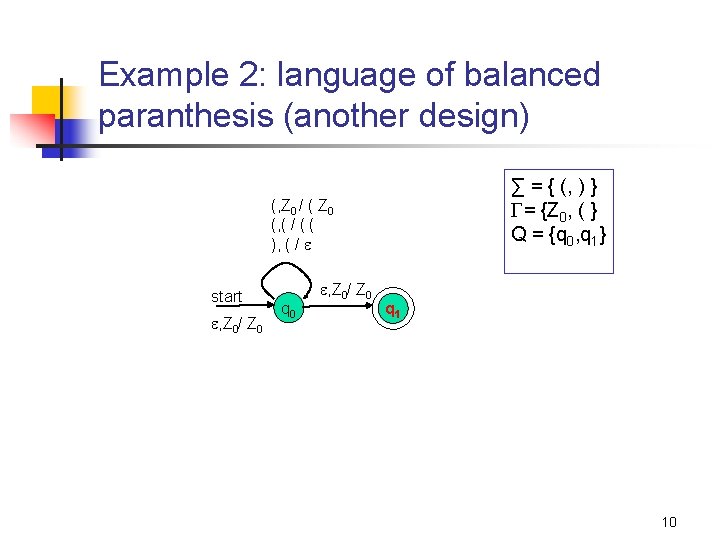
Example 2: language of balanced paranthesis (another design) ∑ = { (, ) } = {Z 0, ( } Q = {q 0, q 1} (, Z 0 / ( Z 0 (, ( / ( ( ), ( / start , Z 0/ Z 0 q 0 , Z 0/ Z 0 q 1 10

PDA’s Instantaneous Description (ID) A PDA has a configuration at any given instance: (q, w, y) n n n q - current state w - remainder of the input (i. e. , unconsumed part) y - current stack contents as a string from top to bottom of stack If δ(q, a, X)={(p, A)} is a transition, then the following are also true: n (q, a, X ) |--- (p, , A) n (q, aw, XB ) |--- (p, w, AB) |--- sign is called a “turnstile notation” and represents one move |---* sign represents a sequence of moves 11

How does the PDA for Lwwr work on input “ 1111”? All moves made by the non-deterministic PDA (q 0, 1111, Z 0) (q 0, 111, 1 Z 0) (q 0, 11 Z 0) (q 0, 1, 111 Z 0) (q 1, 1111, Z 0) (q 1, 111, 1 Z 0) Path dies… (q 1, 11 Z 0) (q 1, 1, 111 Z 0) (q 1, 1, 1 Z 0) Acceptance by final state: (q 1, , 1111 Z 0) (q 1, , Z 0) Path dies… = empty input AND final state (q 0, , 1111 Z 0) (q 2, , Z 0) 12

There are two types of PDAs that one can design: those that accept by final state or by empty stack Acceptance by… n PDAs that accept by final state: n For a PDA P, the language accepted by P, denoted by L(P) by final state, is: Checklist: n n {w | (q 0, w, Z 0) |---* (q, , A) }, s. t. , q F - input exhausted? - in a final state? PDAs that accept by empty stack: n For a PDA P, the language accepted by P, denoted by N(P) by empty stack, is: n {w | (q 0, w, Z 0) |---* (q, , ) }, for any q Q. Q) Does a PDA that accepts by empty stack need any final state specified in the design? Checklist: - input exhausted? - is the stack empty? 14

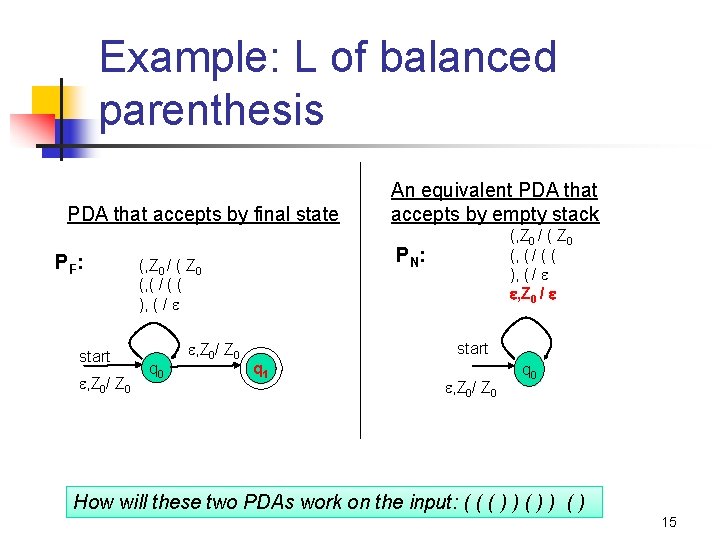
Example: L of balanced parenthesis PDA that accepts by final state PF : start , Z 0/ Z 0 q 0 (, Z 0 / ( Z 0 (, ( / ( ( ), ( / , Z 0 / PN: (, Z 0 / ( Z 0 (, ( / ( ( ), ( / , Z 0/ Z 0 An equivalent PDA that accepts by empty stack start q 1 , Z 0/ Z 0 q 0 How will these two PDAs work on the input: ( ( ( ) ) ( ) 15

PDAs accepting by final state and empty stack are equivalent n PF <= PDA accepting by final state n n PN <= PDA accepting by empty stack n n PF = (QF, ∑, , δF, q 0, Z 0, F) PN = (QN, ∑, , δN, q 0, Z 0) Theorem: n (PN==> PF) For every PN, there exists a PF s. t. L(PF)=L(PN) n (PF==> PN) For every PF, there exists a PN s. t. L(PF)=L(PN) 17

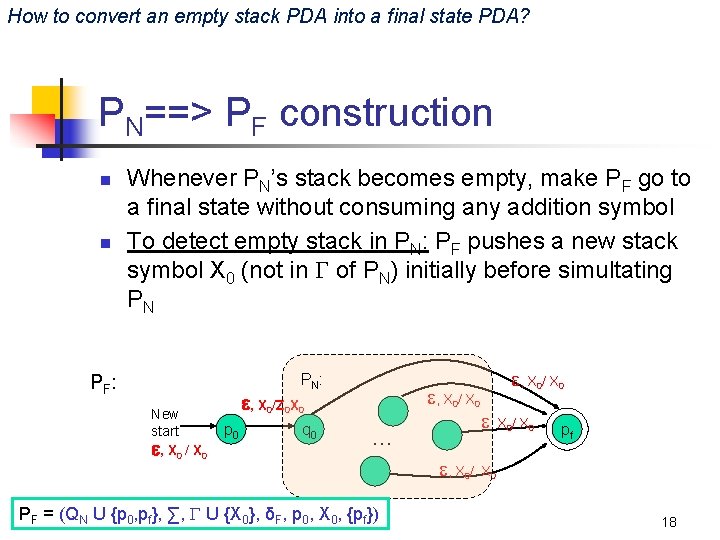
How to convert an empty stack PDA into a final state PDA? PN==> PF construction n n Whenever PN’s stack becomes empty, make PF go to a final state without consuming any addition symbol To detect empty stack in PN: PF pushes a new stack symbol X 0 (not in of PN) initially before simultating PN P N: PF : New start , X 0 / X 0 , X 0/Z 0 X 0 p 0 q 0 … PF = (QN U {p 0, pf}, ∑, P N U {X 0}, δF, p 0, X 0, {pf}) , X 0/ X 0 pf X 0 18

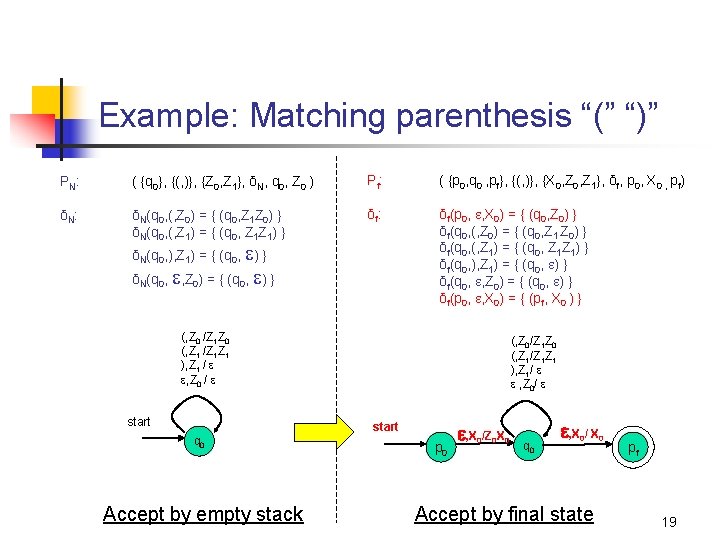
Example: Matching parenthesis “(” “)” PN : ( {q 0}, {(, )}, {Z 0, Z 1}, δN, q 0, Z 0 ) Pf : ( {p 0, q 0 , pf}, {(, )}, {X 0, Z 1}, δf, p 0, X 0 , pf) δN : δN(q 0, (, Z 0) = { (q 0, Z 1 Z 0) } δN(q 0, (, Z 1) = { (q 0, Z 1 Z 1) } δf : δf(p 0, , X 0) = { (q 0, Z 0) } δf(q 0, (, Z 0) = { (q 0, Z 1 Z 0) } δf(q 0, (, Z 1) = { (q 0, Z 1 Z 1) } δf(q 0, ), Z 1) = { (q 0, ) } δf(q 0, , Z 0) = { (q 0, ) } δf(p 0, , X 0) = { (pf, X 0 ) } δN(q 0, ), Z 1) = { (q 0, ) } δN(q 0, , Z 0) = { (q 0, ) } (, Z 0 /Z 1 Z 0 (, Z 1 /Z 1 Z 1 ), Z 1 / , Z 0 / start (, Z 0/Z 1 Z 0 (, Z 1/Z 1 Z 1 ), Z 1/ , Z 0/ start q 0 Accept by empty stack p 0 , X /Z X 0 0 0 q 0 , X / X 0 Accept by final state 0 pf 19

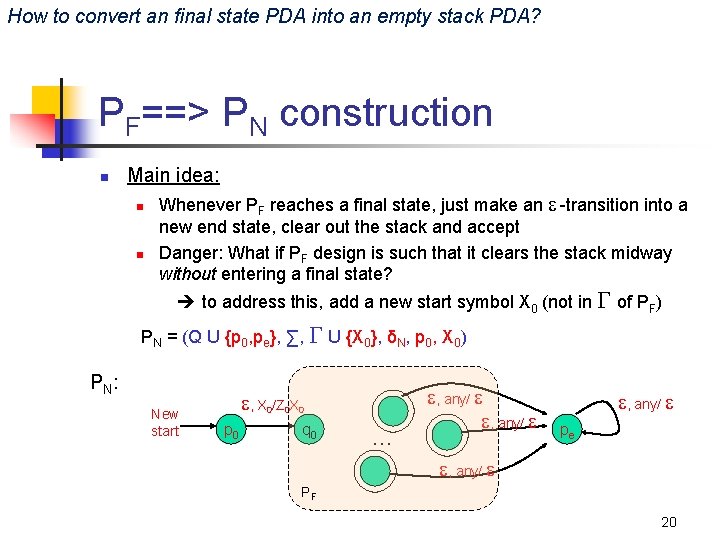
How to convert an final state PDA into an empty stack PDA? PF==> PN construction n Main idea: n n Whenever PF reaches a final state, just make an -transition into a new end state, clear out the stack and accept Danger: What if PF design is such that it clears the stack midway without entering a final state? to address this, add a new start symbol X 0 (not in of PF) PN = (Q U {p 0, pe}, ∑, U {X 0}, δN, p 0, X 0) PN: New start , X 0/Z 0 X 0 p 0 q 0 … , any/ pe , any/ PF 20

Equivalence of PDAs and CFGs 21

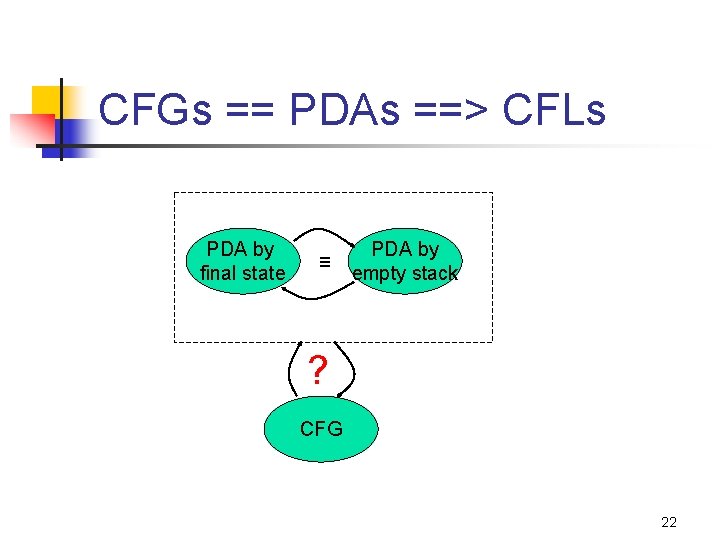
CFGs == PDAs ==> CFLs PDA by final state ≡ PDA by empty stack ? CFG 22

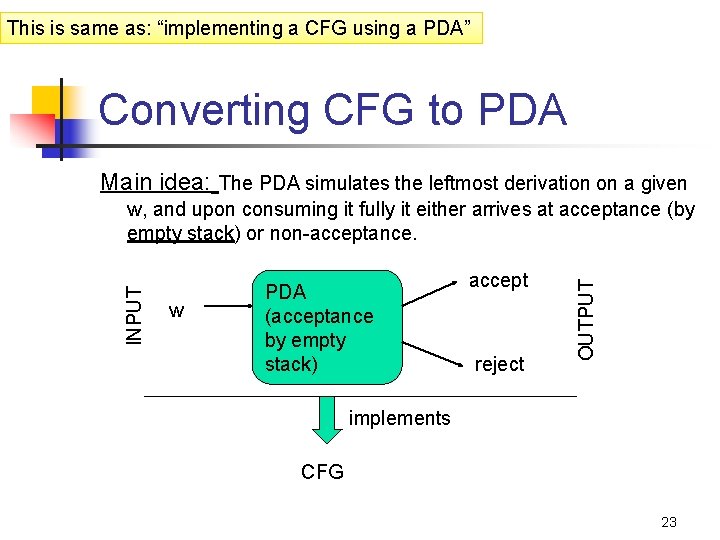
This is same as: “implementing a CFG using a PDA” Converting CFG to PDA Main idea: The PDA simulates the leftmost derivation on a given w PDA (acceptance by empty stack) accept reject OUTPUT INPUT w, and upon consuming it fully it either arrives at acceptance (by empty stack) or non-acceptance. implements CFG 23

This is same as: “implementing a CFG using a PDA” Converting a CFG into a PDA Main idea: The PDA simulates the leftmost derivation on a given w, and upon consuming it fully it either arrives at acceptance (by empty stack) or non-acceptance. Steps: 1. 2. 3. Push the right hand side of the production onto the stack, with leftmost symbol at the stack top If stack top is the leftmost variable, then replace it by all its productions (each possible substitution will represent a distinct path taken by the non-deterministic PDA) If stack top has a terminal symbol, and if it matches with the next symbol in the input string, then pop it State is inconsequential (only one state is needed) 24

Formal construction of PDA Note: Initial stack symbol (S) from CFG same as the start variable in the grammar n n n Before: Given: G= (V, T, P, S) Output: PN = ({q}, T, V U T, δ, q, S) δ: n A n Before: a n δ(q, , A) = { (q, ) | “A ==> ” P} n δ(q, a, a)= { (q, ) } After: a… a pop … … For all a T, add the following transition(s) in the PDA: After: … … For all A V , add the following transition(s) in the PDA: 25

Example: CFG to PDA n n G = ( {S, A}, {0, 1}, P, S) P: n n 1, 1 / 0, 0 / , A / 01 , A / A 1 , A / 0 A 1 , S / AS S ==> AS | A ==> 0 A 1 | 01 , S / S PDA = ({q}, {0, 1, A, S}, δ, q, S) δ: n n q δ(q, , S) = { (q, AS), (q, )} δ(q, , A) = { (q, 0 A 1), (q, 01) } δ(q, 0, 0) = { (q, ) } δ(q, 1, 1) = { (q, ) } How will this new PDA work? Lets simulate string 0011 26

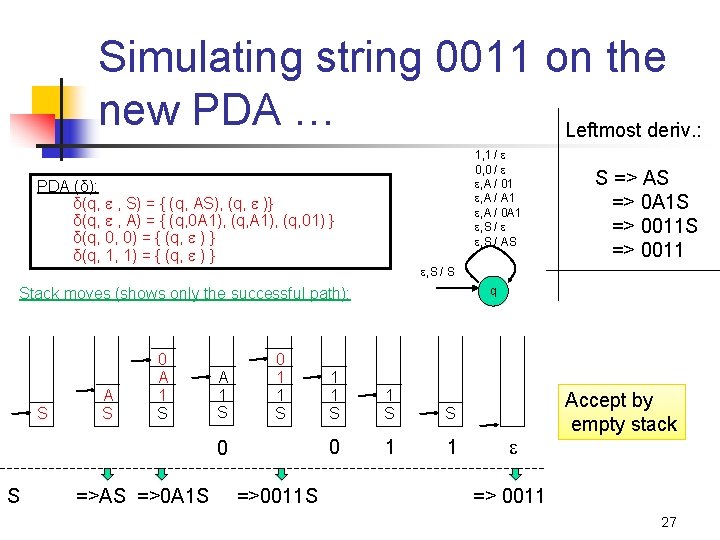
Simulating string 0011 on the new PDA … Leftmost deriv. : 1, 1 / 0, 0 / , A / 01 , A / A 1 , A / 0 A 1 , S / AS PDA (δ): δ(q, , S) = { (q, AS), (q, )} δ(q, , A) = { (q, 0 A 1), (q, 01) } δ(q, 0, 0) = { (q, ) } δ(q, 1, 1) = { (q, ) } , S / S Stack moves (shows only the successful path): S A S 0 A 1 S 0 1 1 S 0 S =>AS =>0 A 1 S =>0011 S S => AS => 0 A 1 S => 0011 q 1 1 S S 0 1 1 Accept by empty stack => 0011 27

Converting a PDA into a CFG Main idea: Reverse engineer the productions from transitions If δ(q, a, Z) => (p, Y 1 Y 2 Y 3…Yk): n 1. 2. 3. n Action: Create a grammar variable called “[q. Zp]” which includes the following production: n n State is changed from q to p; Terminal a is consumed; Stack top symbol Z is popped and replaced with a sequence of k variables. [q. Zp] => a[p. Y 1 q 1] [q 1 Y 2 q 2] [q 2 Y 3 q 3]… [qk-1 Ykqk] Proof discussion (in the book) 29

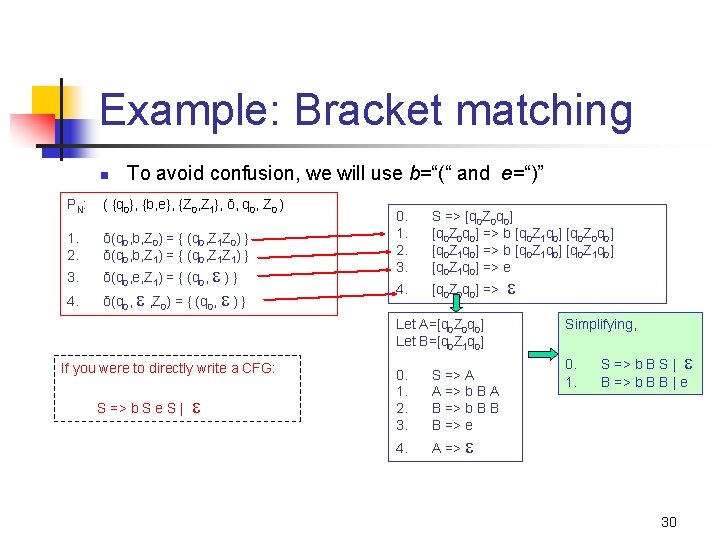
Example: Bracket matching n To avoid confusion, we will use b=“(“ and e=“)” PN : ( {q 0}, {b, e}, {Z 0, Z 1}, δ, q 0, Z 0 ) 1. 2. δ(q 0, b, Z 0) = { (q 0, Z 1 Z 0) } δ(q 0, b, Z 1) = { (q 0, Z 1 Z 1) } 3. 4. δ(q 0, e, Z 1) = { (q 0, ) } δ(q 0, , Z 0) = { (q 0, ) } 0. 1. 2. 3. S => [q 0 Z 0 q 0] => b [q 0 Z 1 q 0] [q 0 Z 0 q 0] [q 0 Z 1 q 0] => b [q 0 Z 1 q 0] => e 4. [q 0 Z 0 q 0] => Let A=[q 0 Z 0 q 0] Let B=[q 0 Z 1 q 0] If you were to directly write a CFG: S => b S e S | 0. 1. 2. 3. 4. S => A A => b B A B => b B B B => e Simplifying, 0. 1. S => b B S | B => b B B | e A => 30

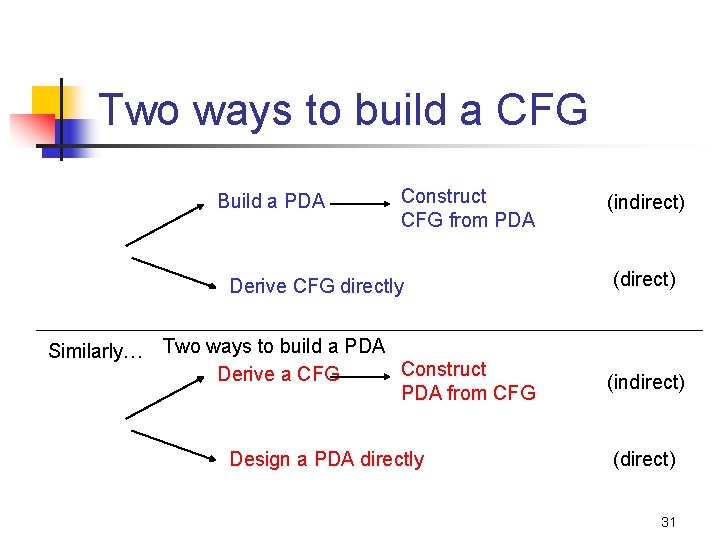
Two ways to build a CFG Build a PDA Construct CFG from PDA Derive CFG directly Similarly… Two ways to build a PDA Construct Derive a CFG PDA from CFG Design a PDA directly (indirect) (direct) 31

Deterministic PDAs 32

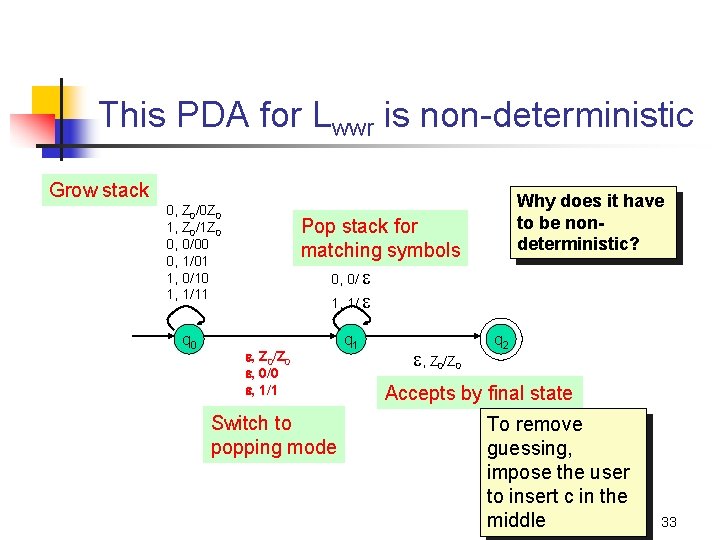
This PDA for Lwwr is non-deterministic Grow stack 0, Z 0/0 Z 0 1, Z 0/1 Z 0 0, 0/00 0, 1/01 1, 0/10 1, 1/11 q 0 Why does it have to be nondeterministic? Pop stack for matching symbols 0, 0/ 1, 1/ , Z 0/Z 0 , 0/0 , 1/1 Switch to popping mode q 1 , Z 0/Z 0 q 2 Accepts by final state To remove guessing, impose the user to insert c in the middle 33

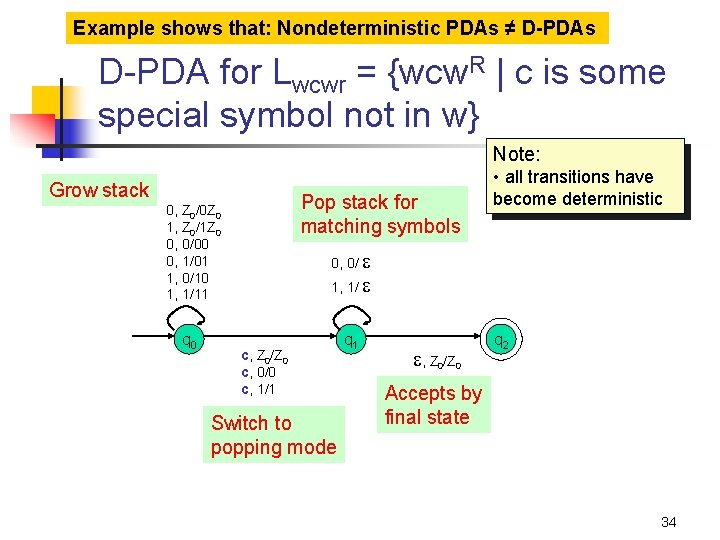
Example shows that: Nondeterministic PDAs ≠ D-PDAs D-PDA for Lwcwr = {wcw. R | c is some special symbol not in w} Note: Grow stack Pop stack for matching symbols 0, Z 0/0 Z 0 1, Z 0/1 Z 0 0, 0/00 0, 1/01 1, 0/10 1, 1/11 q 0 • all transitions have become deterministic 0, 0/ 1, 1/ c, Z 0/Z 0 c, 0/0 c, 1/1 Switch to popping mode q 1 , Z 0/Z 0 q 2 Accepts by final state 34

Deterministic PDA: Definition n A PDA is deterministic if and only if: 1. δ(q, a, X) has at most one member for any a ∑ U { } If δ(q, a, X) is non-empty for some a ∑, then δ(q, , X) must be empty. 35

PDA vs DPDA vs Regular languages Lwcwr Regular languages Lwwr D-PDA non-deterministic PDA 36

Summary PDAs for CFLs and CFGs n n n Non-deterministic Deterministic PDA acceptance types n 1. 2. By final state By empty stack PDA n n IDs, Transition diagram Equivalence of CFG and PDA n n n CFG => PDA construction PDA => CFG construction 37