PUSHDOWN AUTOMATA PDA CSE501 FORMAL LANGUAGE AUTOMATA THEORY

PUSHDOWN AUTOMATA (PDA) CSE-501 FORMAL LANGUAGE & AUTOMATA THEORY Aug-Dec, 2010 ALAK ROY. Assistant Professor Dept. of CSE NIT Agartala

PUSHDOWN AUTOMATA (PDA) Informally: � Think of an ε-NFA with the additional power that it can manipulate a stack. � Transitions are modified to accommodate stack operations. Questions: What is a stack? � How does a stack help? � Why PDA? � A DFA can “remember” only a finite amount of information, whereas a PDA can “remember” an infinite amount of (certain types of) information. 2

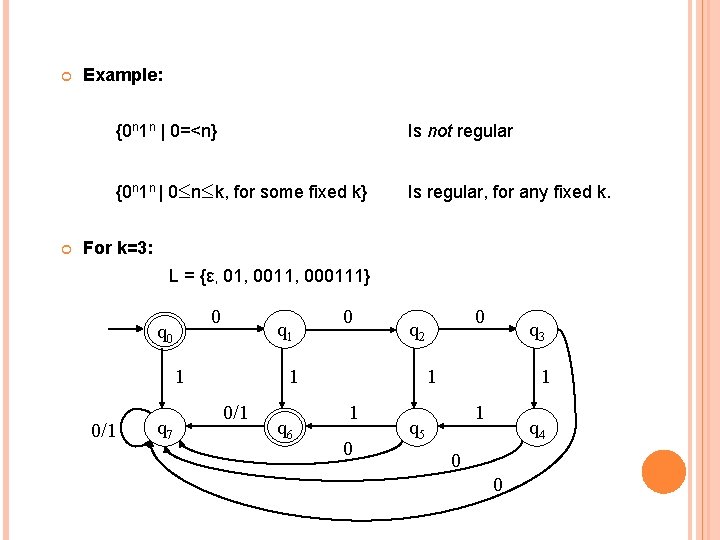
Example: {0 n 1 n | 0=<n} Is not regular {0 n 1 n | 0 n k, for some fixed k} Is regular, for any fixed k. For k=3: L = {ε, 01, 0011, 000111} 0 q 1 1 0/1 q 7 0 q 2 1 0/1 q 6 0 q 3 1 1 0 1 1 q 5 q 4 0 0 3

In a DFA, each state remembers a finite amount of information. To get {0 n 1 n | 0 n} with a DFA would require an infinite number of states using the preceding technique. An infinite stack solves the problem for {0 n 1 n | 0 n} as follows: Read all 0’s and place them on a stack � Read all 1’s and match with the corresponding 0’s on the stack � Only need two states to do this in a PDA Similarly for {0 n 1 m 0 n+m | n, m 0} 4

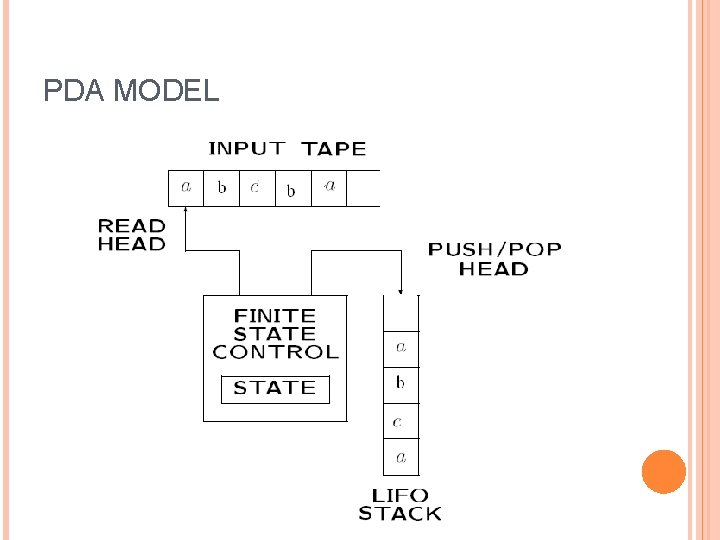
PDA MODEL

CHARACTERISTIC OF PDA PDS (Pushdown Stack)

PDA Being nondeterministic, the PDA can have a choice of next moves. Its moves are determined by: 1. 2. 3. The current state (of its “NFA”), The current input symbol (or ε), and The current symbol on top of its stack. In each choice, the PDA can: 1. 2. Change state, and also Replace the top symbol on the stack by a sequence of zero or more symbols. u u Zero symbols = “pop. ” Many symbols = sequence of “pushes. ” 7

FORMAL DEFINITION OF A PDA A pushdown automaton (PDA) is a seven-tuple: M = (Q, Σ, Г, δ, q 0, z 0, F) Q Σ Г q 0 A finite set of states A finite input alphabet A finite stack alphabet The initial/starting state, q 0 is in Q z 0 F δ A starting stack symbol, is in Г A set of final/accepting states, which is a subset of Q A transition function, where δ: Q x (Σ U {ε}) x Г –> finite subsets of Q x Г* 8

Consider the various parts of δ: Q x (Σ U {ε}) x Г –> finite subsets of Q x Г* Q on the LHS means that at each step in a computation, a PDA must consider its’ current state. � Г on the LHS means that at each step in a computation, a PDA must consider the symbol on top of its’ stack. � Σ U {ε} on the LHS means that at each step in a computation, a PDA may or may not consider the current input symbol, i. e. , it may have epsilon transitions. � “Finite subsets” on the RHS means that at each step in a computation, a PDA will have several options. � Q on the RHS means that each option specifies a new state. � Г* on the RHS means that each option specifies zero or more stack symbols that will replace the top stack symbol. � 9

CONVENTIONS a, b, … are input symbols. � But sometimes we allow ε as a possible value. …, X, Y, Z are stack symbols. …, w, x, y, z are strings of input symbols. , , … are strings of stack symbols. 10

THE TRANSITION FUNCTION Takes three arguments: 1. 2. 3. A state, in Q. An input, which is either a symbol in Σ or ε. A stack symbol in Γ. δ(q, a, Z) is a set of zero or more actions of the form (p, ). � p is a state; is a string of stack symbols. 11

ACTIONS OF THE PDA If δ(q, a, Z) contains (p, ) among its actions, then one thing the PDA can do in state q, with a at the front of the input, and Z on top of the stack is: 1. 2. 3. Change the state to p. Remove a from the front of the input (but a may be ε). Replace Z on the top of the stack by . (or Pop Z, Push ) 12

Two types of PDA transitions: δ(q, a, z) = {(p 1, 1), (p 2, 2), …, (pm, m)} � � � Current state is q Current input symbol is a Symbol currently on top of the stack z Move to state pi from q Replace z with i on the stack (leftmost symbol on top) Move the input head to the next input symbol q a/z/ 1 p 1 a/z/ 2 p 2 a/z/ m : pm 13

Two types of PDA transitions: δ(q, ε, z) = {(p 1, 1), (p 2, 2), …, (pm, m)} � � � Current state is q Current input symbol is not considered Symbol currently on top of the stack z Move to state pi from q Replace z with i on the stack (leftmost symbol on top) No input symbol is read q ε/z/ 1 p 1 ε/z/ 2 p 2 ε/z/ m : pm 14

EXAMPLE: PDA Design a PDA to accept {0 n 1 n | n > 1}. The states: �q = start state. We are in state q if we have seen only 0’s so far. � p = we’ve seen at least one 1 and may now proceed only if the inputs are 1’s. � f = final state; accept. 15

EXAMPLE: PDA – (2) The stack symbols: � Z 0 = start symbol. Also marks the bottom of the stack, so we know when we have counted the same number of 1’s as 0’s. � X = marker, used to count the number of 0’s seen on the input. 16

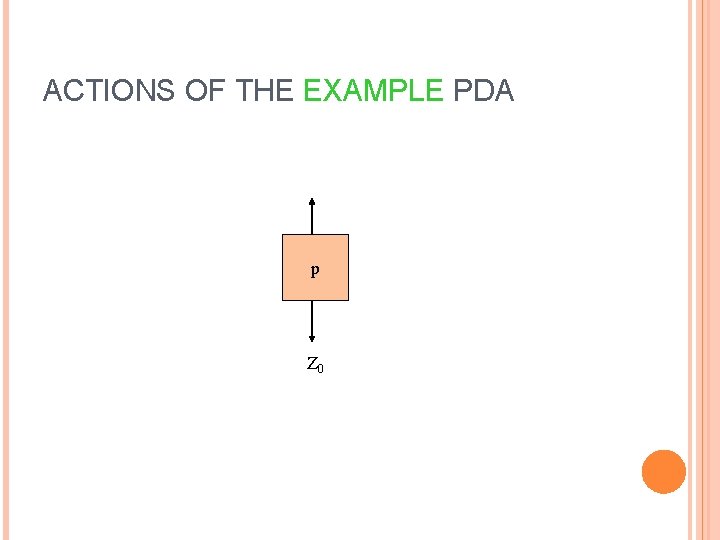
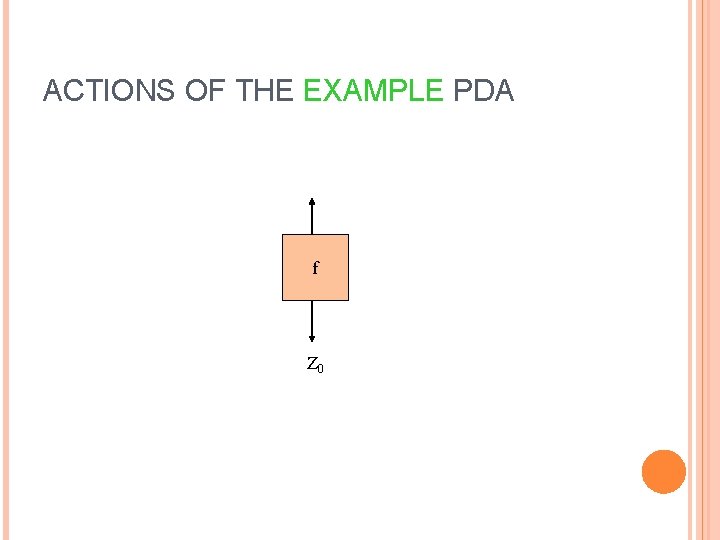
EXAMPLE: PDA – (3) The transitions: � δ(q, 0, Z 0) = {(q, XZ 0)}. � δ(q, 0, X) = {(q, XX)}. These two rules cause one X to be pushed onto the stack for each 0 read from the input. � δ(q, 1, X) = {(p, ε)}. When we see a 1, go to state p and pop one X. � δ(p, 1, X) = {(p, ε)}. Pop one X per 1. � δ(p, ε, Z 0) = {(f, Z 0)}. Accept at bottom. 17

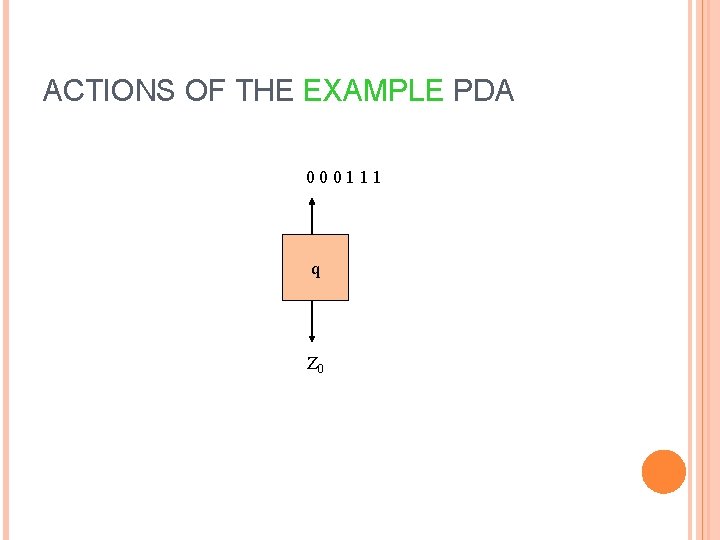
ACTIONS OF THE EXAMPLE PDA 000111 q Z 0

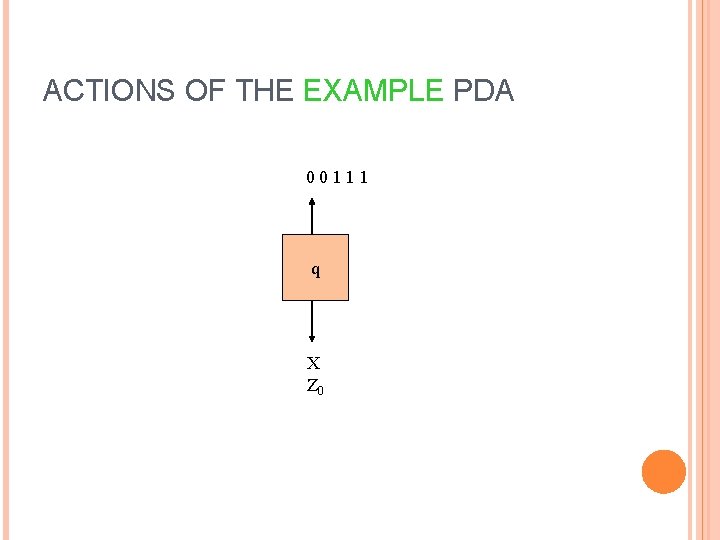
ACTIONS OF THE EXAMPLE PDA 00111 q X Z 0

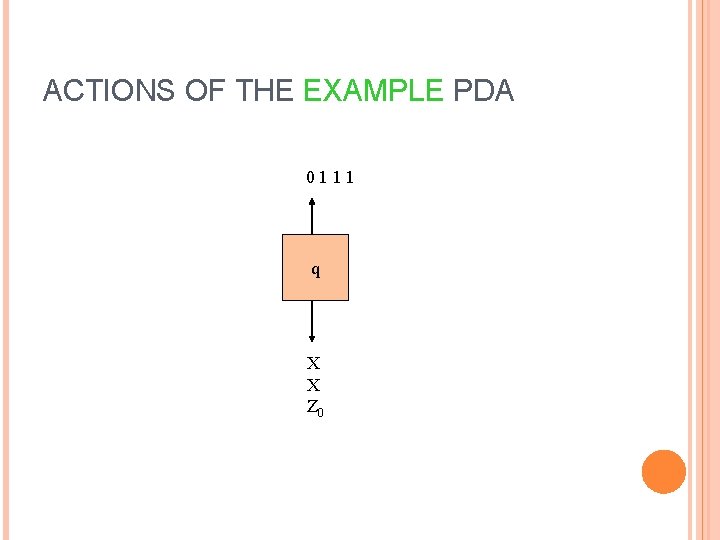
ACTIONS OF THE EXAMPLE PDA 0111 q X X Z 0

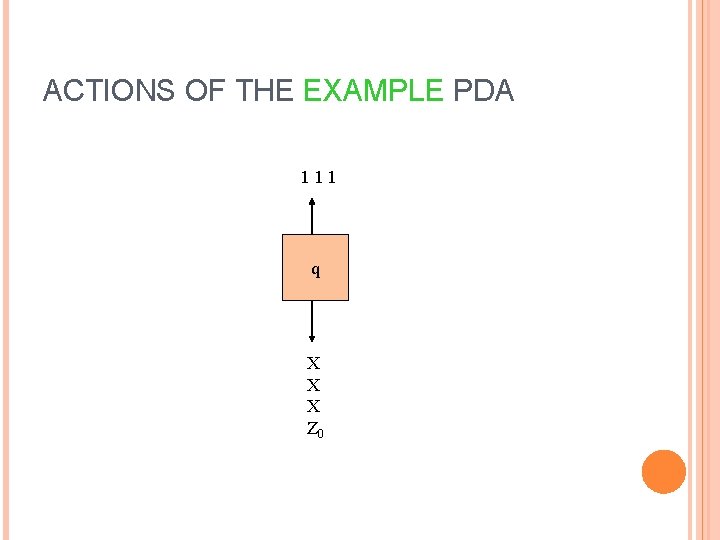
ACTIONS OF THE EXAMPLE PDA 111 q X X X Z 0

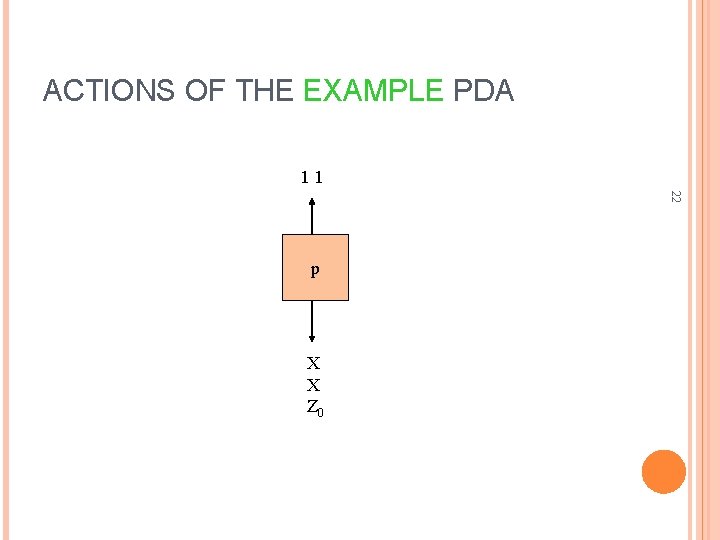
ACTIONS OF THE EXAMPLE PDA 11 22 p X X Z 0

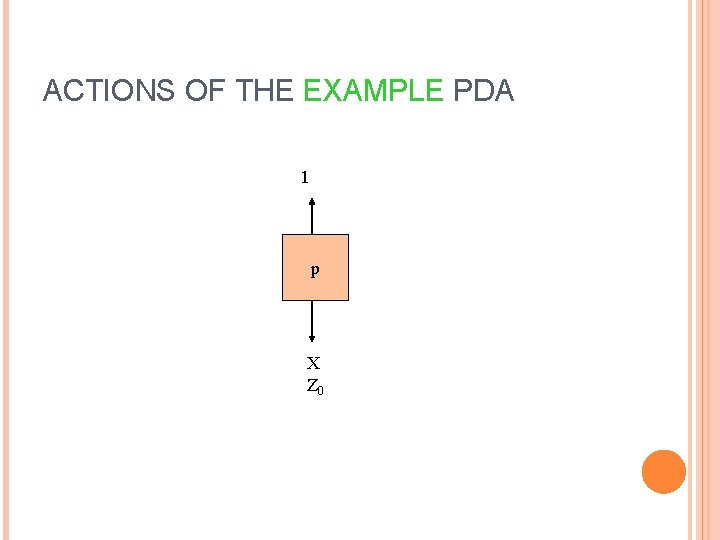
ACTIONS OF THE EXAMPLE PDA 1 p X Z 0

ACTIONS OF THE EXAMPLE PDA p Z 0

ACTIONS OF THE EXAMPLE PDA f Z 0

THANK YOU