Pushdown Automata Part II PDAs and CFG Chapter

Pushdown Automata Part II: PDAs and CFG Chapter 12 1

PDAs and Context-Free Grammars Theorem: The class of languages accepted by PDAs is exactly the class of context-free languages. Recall: context-free languages are languages that can be defined with context-free grammars. Restate theorem: Can describe with context-free grammar Can accept by PDA 2

Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack do the work. Two approaches: • Top down • Bottom up 3

Top Down The idea: Let the stack keep track of expectations. Example: Arithmetic expressions E E+T E T T T F F (E) F id (1) (2) (3) (4) (5) (6) (q, , E), (q, E+T) (q, , E), (q, T) (q, , T), (q, T*F) (q, , T), (q, F) (q, , F), (q, (E) ) (q, , F), (q, id) (7) (q, id), (q, ) (8) (q, (, ( ), (q, ) (9) (q, ), ) ), (q, ) (10) (q, +, +), (q, ) (11) (q, , ), (q, ) 4

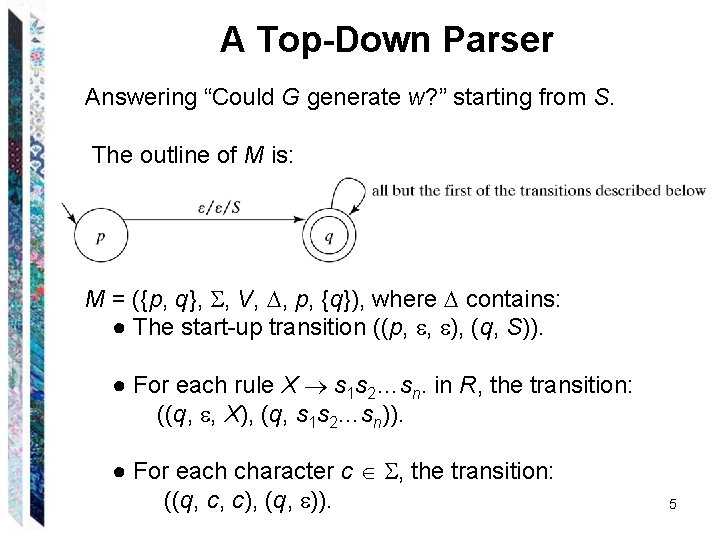
A Top-Down Parser Answering “Could G generate w? ” starting from S. The outline of M is: M = ({p, q}, , V, , p, {q}), where contains: ● The start-up transition ((p, , ), (q, S)). ● For each rule X s 1 s 2…sn. in R, the transition: ((q, , X), (q, s 1 s 2…sn)). ● For each character c , the transition: ((q, c, c), (q, )). 5

Example of the Construction L = {anb*an} (1) S (2) S B (3) S a. Sa (4) B (5) B b. B input = a a b b a a trans 0 3 6 2 5 7 4 6 6 state p q q q q 0 (p, , ), (q, S) 1 (q, , S), (q, ) 2 (q, , S), (q, B) 3 (q, , S), (q, a. Sa) 4 (q, , B), (q, ) 5 (q, , B), (q, b. B) 6 (q, a, a), (q, ) 7 (q, b, b), (q, ) unread input a a b b a b b b b b a a a a a a a stack S a. Sa Sa a. Saa Baa b. Baa Baa aa a 6

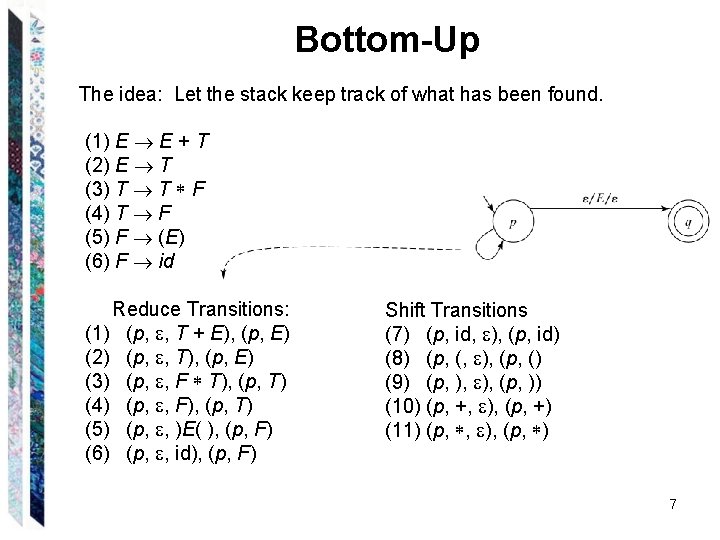
Bottom-Up The idea: Let the stack keep track of what has been found. (1) E E + T (2) E T (3) T T F (4) T F (5) F (E) (6) F id Reduce Transitions: (1) (p, , T + E), (p, E) (2) (p, , T), (p, E) (3) (p, , F T), (p, T) (4) (p, , F), (p, T) (5) (p, , )E( ), (p, F) (6) (p, , id), (p, F) Shift Transitions (7) (p, id, ), (p, id) (8) (p, (, ), (p, () (9) (p, ), (p, )) (10) (p, +, ), (p, +) (11) (p, , ), (p, ) 7

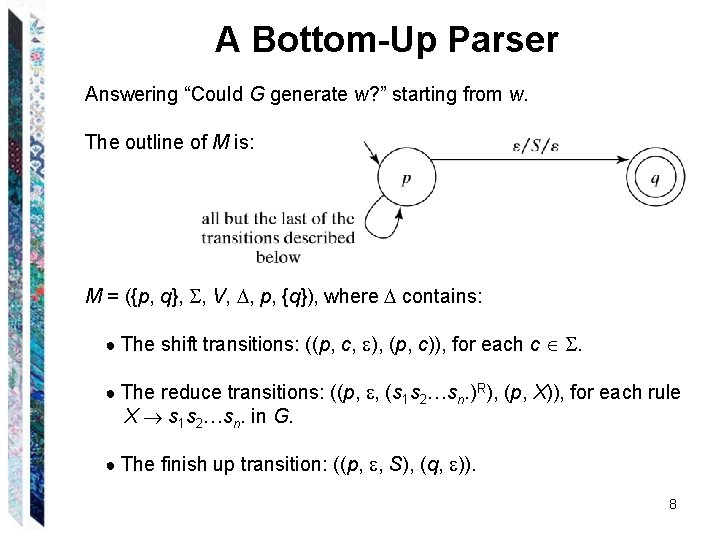
A Bottom-Up Parser Answering “Could G generate w? ” starting from w. The outline of M is: M = ({p, q}, , V, , p, {q}), where contains: ● The shift transitions: ((p, c, ), (p, c)), for each c . ● The reduce transitions: ((p, , (s 1 s 2…sn. )R), (p, X)), for each rule X s 1 s 2…sn. in G. ● The finish up transition: ((p, , S), (q, )). 8

Example of the Construction L = {anb*an} (1) S (2) S B (3) S a. Sa (4) B (5) B b. B input = a a b b a a trans 6 6 7 7 4 5 5 2 6 3 0 state p p p p q 0 (p, , S), (q, ) 1 (p, , ), (p, S) 2 (p, , B), (p, S) 3 (p, , a. Sa), (p, S) 4 (p, , ), (p, B) 5 (p, , Bb), (p, B) 6 (p, a, ), (p, a) 7 (p, b, ), (p, b) unread input a a b b b b b a a a a a stack a aa bbaa Bbaa Baa Saa a. Saa Sa a. Sa S 9

Notice Nondeterminism Machines constructed with the algorithm are often nondeterministic, even when they needn't be. This happens even with trivial languages. Example: An. Bn = {anbn: n 0} A grammar for An. Bn is: [1] S a. Sb [2] S A PDA M built top-down for An. Bn is: (0) (1) (2) (3) (4) ((p, , ), (q, S)) ((q, , S), (q, a. Sb)) ((q, , S), (q, )) ((q, a, a), (q, )) ((q, b, b), (q, )) But transitions 1 and 2 make M nondeterministic. How about bottom-up? A directly constructed machine for An. Bn: 10

Going The Other Way Lemma: If a language is accepted by a pushdown automaton M, it is context-free (i. e. , it can be described by a context-free grammar). Proof (by construction): (We will skip this to Slide 16, as it’s rarely necessarily going this way in practice!) Step 1: Convert M to restricted normal form: ● M has a start state s that does nothing except push a special symbol # onto the stack and then transfer to a state s from which the rest of the computation begins. There must be no transitions back to s. ● M has a single accepting state a. All transitions into a pop # and read no input. ● Every transition in M, except the one from s , pops exactly one symbol from the stack. 11

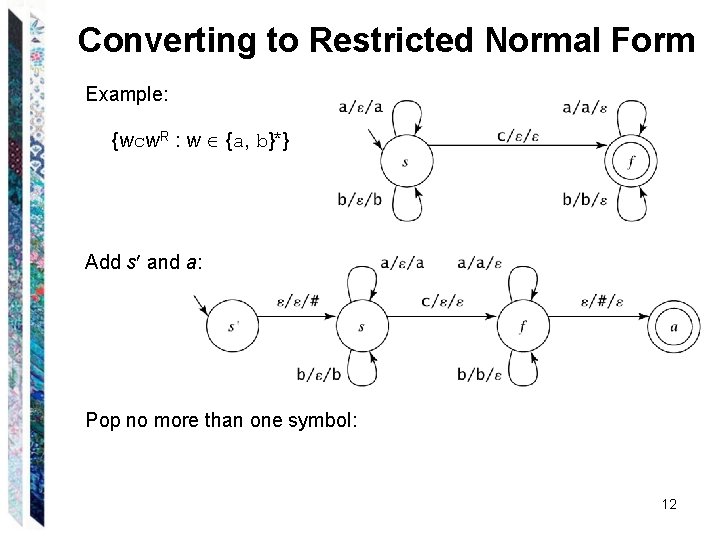
Converting to Restricted Normal Form Example: {wcw. R : w {a, b}*} Add s and a: Pop no more than one symbol: 12

M in Restricted Normal Form [1] [3] Pop exactly one symbol: Replace [1], [2] and [3] with: [1] ((s, a, #), (s, a#)), ((s, a, a), (s, aa)), ((s, a, b), (s, ab)), [2] ((s, b, #), (s, b#)), ((s, b, a), (s, ba)), ((s, b, b), (s, bb)), [3] ((s, c, #), (f, #)), ((s, c, a), (f, a)), ((s, c, b), (f, b)) [2] Must have one transition for everything that could have been on the top of the stack so it can be popped and then pushed back on. 13

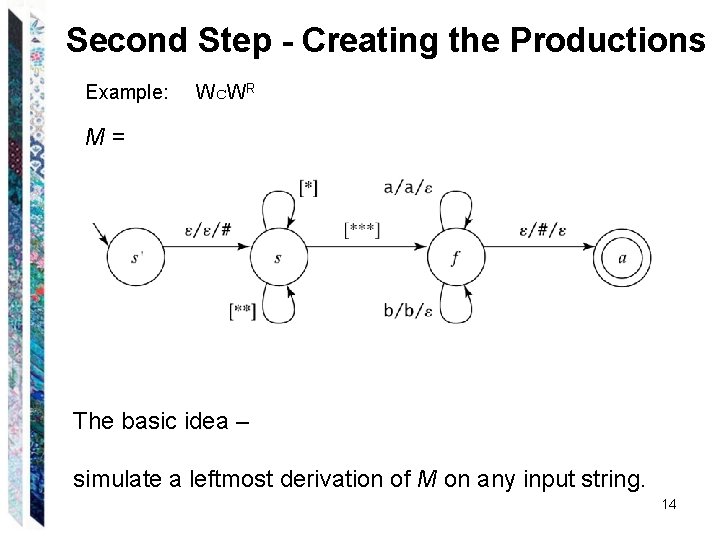
Second Step - Creating the Productions Example: Wc. WR M= The basic idea – simulate a leftmost derivation of M on any input string. 14

Second Step - Creating the Productions Example: abcba 15

Nondeterminism and Halting 1. There are context-free languages for which no deterministic PDA exists. 2. It is possible that a PDA may ● not halt, ● not ever finish reading its input. 3. There exists no algorithm to minimize a PDA. It is undecidable whether a PDA is minimal. 16

Nondeterminism and Halting It is possible that a PDA may ● not halt, ● not ever finish reading its input. Let = {a} and consider M = L(M) = {a}: (1, a, ) |- (2, a, a) |- (3, , ) On any other input except a: ● M will never halt. ● M will never finish reading its input unless its input is . Example: aa 17

Solutions to the Problem ● For NDFSMs: ● Convert to deterministic, or ● Simulate all paths in parallel. ● For NDPDAs: ● Impossible to simulate all paths in parallel – each path would need its won stack ● Formal solutions usually involve changing the grammar parse tree may not make sense ● Practical solutions that: ● Preserve the structure of the grammar, but ● Only work on a subset of the CFLs. 18

Alternative Equivalent Definitions of a PDA (Skip to Slide 21) Accept by accepting state at end of string (i. e. , we don't care about the stack). From M (in our definition) we build M (in this one): 1. Initially, let M = M. 2. Create a new start state s. Add the transition: ((s , , ), (s, #)). 3. Create a new accepting state qa. 4. For each accepting state a in M do, 4. 1 Add the transition ((a, , #), (qa, )). 5. Make qa the only accepting state in M. 19

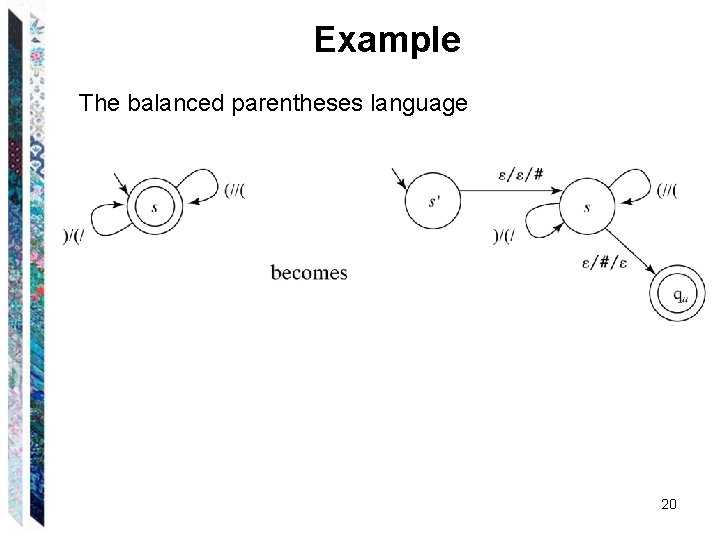
Example The balanced parentheses language 20

What About These? ● FSM plus FIFO queue (instead of stack)? ● FSM plus two stacks? 21

Comparing Regular and Context-Free Languages Regular Languages ● regular exprs. ● or ● regular grammars ● recognize ● = DFSMs Context-Free Languages ● context-free ● parse ● = NDPDAs 22