Pushdown Automata CPSC 388 Ellen Walker Hiram College

Pushdown Automata CPSC 388 Ellen Walker Hiram College

PDA = FA + Stack

A PDA Transaction • • Read the next symbol from the input Pop a symbol from the stack Push a symbol on the stack Enter a new state

Epsilon in PDA • Read epsilon – No character is read, input location stays the same • Push or pop epsilon – The stack remains unchanged

Format of a Transition • Items before ; are “input”, items after ; are “action” ( Current state, Input symbol, Symbol popped ; New state, Symbol pushed )

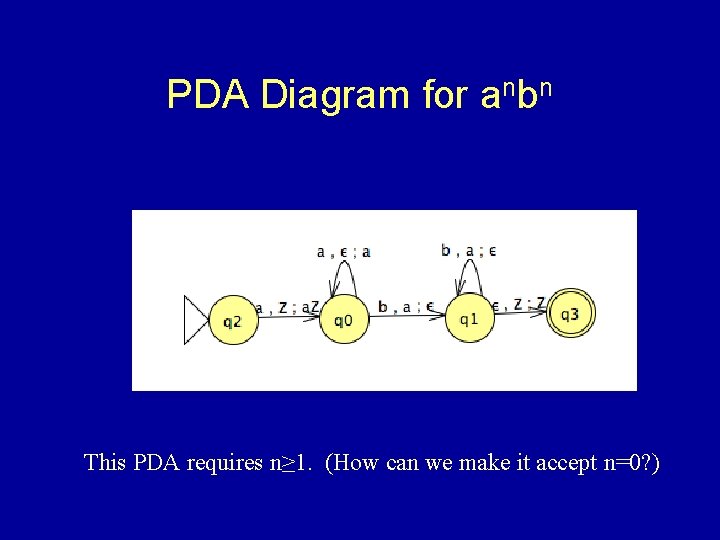
PDA for anbn • Assume initial stack contains “Z” (delimiter for bottom of stack) • S 1, a, ; S 2, a - leave Z on bottom • S 2, a, ; S 2, a - push a for each a • S 2, b, a ; S 3, - pop a for each b • S 3, b, a ; S 3, • S 3, , Z ; S 4, Z - Final state if Z reached

PDA Diagram • For each state: item read, popped, pushed • State transitions using arrows as for FA • To check the item on top of the stack, then push an additional item, JFLAP allows a double-push (a, Z, a. Z)

PDA Diagram for anbn This PDA requires n≥ 1. (How can we make it accept n=0? )

Formal Definition of PDA • A PDA is of the form (S, , , F) where –S is a finite collection of states – is the machine's alphabet – is the finite collection of stack symbols – is the finite collection of transitions of the form (p, s, x; q, y) – (an element of S) is the initial state –F (a subset of S) is the set of accept states

Formal Definition of Example • States: {q 0, q 1, q 2, q 3} • Alphabet: {a, b} • Stack symbols: {Z, a} • Transitions (see slide 6) • Initial state: q 2 • Accept states: {q 3}

All Strings with Equal # a’s and b’s • General idea: – If you see an a • If there is a b on the stack, pop it • Otherwise, push an a – If you see a b • If there is an a on the stack, pop it • Otherwise, push a b – At the end of the string, if Z is on top, then accept

Build a PDA for each: • All strings of the form ambn, n>m • All strings consisting of a’s and b’s with at least 3 more a’s than b’s (Hint: use epsilon-transitions) • All palindromes over the alphabet {a, b, c} (Hint: it needs to be nondeterministic)

Every RL has a PDA to accept it • Given the RL, construct an FA for it. • Make a PDA with the same FA that reads the input but ignores the stack – For each FA transition (state 1, char; state 2) create a pda transition (state 1, char, ; state 2, )

PDA’s are more powerful than FA’s • Every FA has an equivalent PDA – Proof by construction on previous slide • At least one PDA does not have an equivalent FA – Proof by example: anbn • Therefore the class of languages accepted by PDA’s is a superset of the class of languages accepted by FA’s

Deterministic vs. Nondeterministic PDA’s • Deterministic PDA’s – Every state/stack combination has exactly one transition – No epsilon-transitions (epsilon for both input and stack symbol) • Nondeterministic PDA’s are more powerful than deterministic PDA’s – Example: strings from a*b* that have either twice as many a’s as b’s or 3 x as many a’s as b’s

Not All Languages are Context Free • There is a pumping lemma for Context free languages • Similar to RL pumping lemma, but you have to pump in two places • Non CFL: anbncn • (Details are beyond the scope of this course)