Pushdown Automata Chapters 14 18 Generators vs Recognizers

Pushdown Automata Chapters 14 -18

Generators vs. Recognizers • For Regular Languages: – regular expressions are generators – FAs are recognizers • For Context-free Languages – CFGs are generators – Pushdown Automata (PDAs) are recognizers

All regular languages can be generated by CFGs and so can some non-regular languages Languages generated by CFGs Languages defined by regular expressions

PDA vs. FA • Add a stack • Each transition can specify optional push and pop operations – using an independent alphabet – use Λ (or e) to ignore stack operations • a, e/A means with input ‘a’, pop nothing, push an ‘A’ • Can use accepting states for success – Or can just use an empty stack – We’ll do both simultaneously (usually)

Example: anbn

Example: anbn • Every input ‘a’ pushes a ‘A’ on the stack • Every input ‘b’ pops an ‘A’ off the stack – if any other character appears, reject • At end of input, the stack should be empty – else the count was off, and we should reject • Code: anbn. cpp

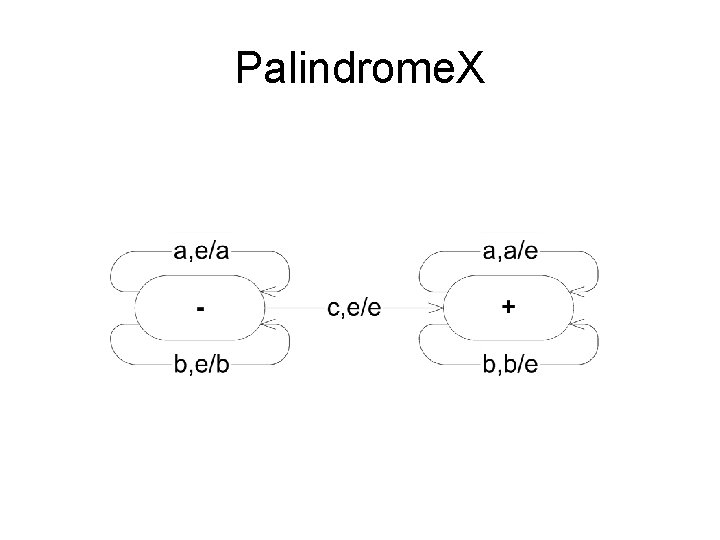
Example: Palindrome. X • Accepts strings of the form wcw. R • Pops the first half onto the stack • We need the middle delimiter to know when to start comparing in reverse – otherwise, the process would be non-deterministic – each popped character should match the corresponding input character • Diagram on next slide • Code: palindromex. cpp

Palindrome. X

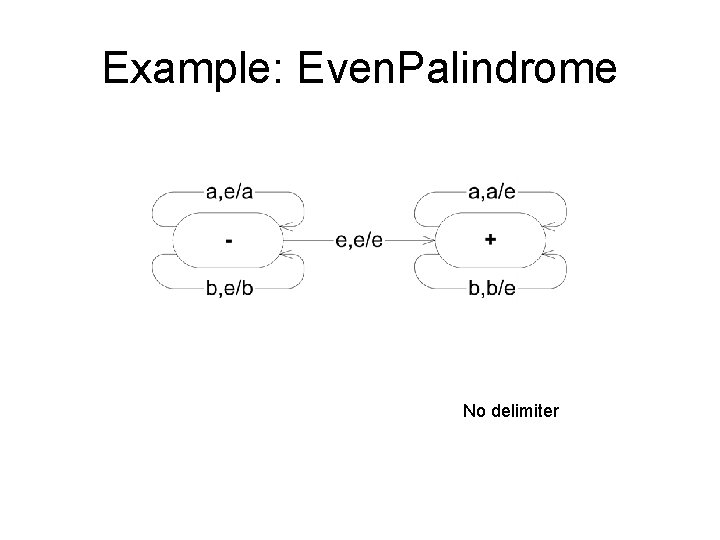
Example: Even. Palindrome No delimiter

Determinism vs. Non-determinism • Deterministic if: – Only one transition exists for each combination of (q, a, X) = (state, input letter, stack top) – If a = e, then no other rule exists for that q and X • Other, multiple moves for the same state/input/stack are possible • As long as an acceptable path exists, the machine accepts the input • Interesting note: – The class of languages accepted by NPDAs is larger than those accepted by DPDAs!

PDA more powerful than FA Languages accepted by nondeterministic PDA Languages accepted by FA or NFA or TG Languages accepted by deterministic PDA

CFG => PDA • Has two states: – start, accepting • Have an empty move from the start state to the accepting state that pushes the start non-terminal • Cycle on the accepting state: – empty moves that replace variables with each of their rules – moves that consume each terminal

CFG => PDA Example S => e | (S) | SS

Derive (()) • Using CFG (do a leftmost-derivation): – S => (S) =>((S)) => (()) • PDA (non-deterministically) – do by hand, showing stack at each step

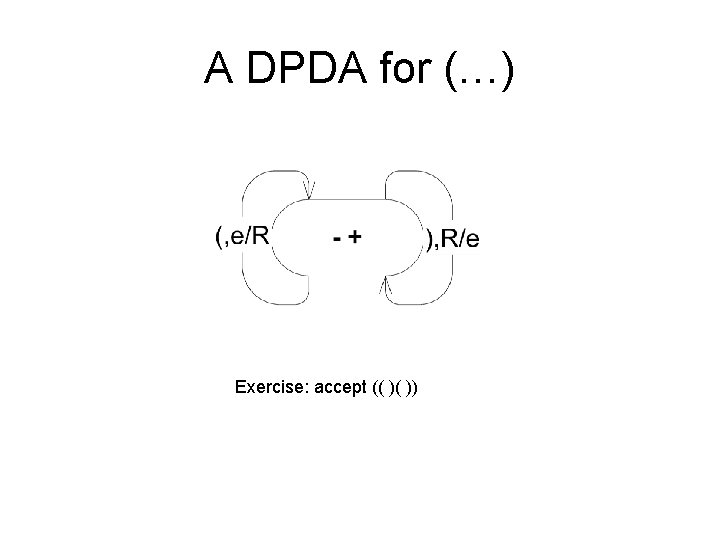
A DPDA for (…) Exercise: accept (( )( ))

CFG vs. PDA • Any CFG can be represented by a PDA – But some CFLs require non-determinism • unlike NFA’s => FAs => regular expressions – i. e. , the languages accepted by DPDAs form a subset of those accepted by NPDAs • Any PDA has a corresponding CFG – Lots of work to find!!!

Converting from PDA to CFG • • A PDA “consumes” a character A CFG “generates” a character We want to relate these two What happens when a PDA consumes a character? – It may change state – It may change the stack

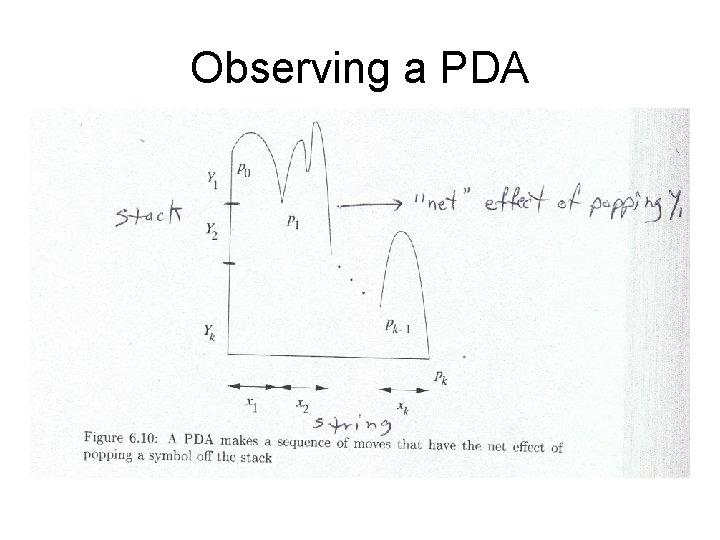
Converting from PDA to CFG continued • Suppose X is on the stack and ‘a’ is read • What can happen to X? – It can be popped – It may replaced by one or more other stack symbols • And so on… • The stack grows and shrinks and grows and shrinks … – Eventually, as more input is consumed, the effect of having X on the stack must be erased (or we’ll never reach an empty stack!) – And the state may change many times – We must track all of this! (see picture next slide)

Observing a PDA

Converting from PDA to CFG continued • Let the symbol <q. Ap> represent the movement in a PDA that starts in state q and ends in state p – This will result in possibly many moves and stack changes – It represents moving from q to p while erasing the net effects of having A on the stack • The symbol <sλf> represents accepting a valid string (if f is a final state) • These symbols will be our variables/non-terminals – Because they track the machine configuration that accepts strings – Our grammar will generate those strings

Converting from PDA to CFG continued • Consider the transition ((q, a, X), (p, Y)) – This means that a is consumed, X is popped, we move to state p, and subsequent processing must erase Y and its subsequent effects • A corresponding grammar rule is: – – <q. X? > => a<p. Y? > (? ’s represent the same state) We don’t know where we’ll eventually end up But we know we immediately go through p So we entertain all possibilities

From Transitions to Grammar Rules • 1) S => <sλf> for all final states, f • 2) <qλq> => λ for all states, q – These serve as terminators • 3) For transitions ((q, a, X), (p, Y)): – <q. Xr> => a<p. Yr> for all states, r • 4) For transitions ((q, a, X), (p, Y 1 Y 2)): – <q. Xr> => a<p. Y 1 s><s. Y 2 r> for all states, r, s – And so on for longer pushed strings

Theoretical Results • Pumping Lemma for CFGs • Closure properties – different from regular languages! • Decidability – we won’t cover most of this (Chapter 18) – you’ll get the important stuff in Compilers – need determinism to do efficient parsing

Infinite CFLs • How can you tell if a CFG generates an infinite language? • CFLPL-1. PDF

Parse Trees from CNF • What do CNF Parse Trees Look Like? • Relate depth of tree to length of possible strings • CFLPL-2. PDF • CFLPL-3. PDF • CFLPL-4. PDF

CNF Parse Trees vs. Strings • We want to go the other way: – determine the possible depths of CNF trees from strings of a given length • CFLPL-5. PDF • CFLPL-6. PDF • CFLPL-7. PDF

The Pumping Lemma for CFGs • Similar to the one for regular languages • Based on self-embedding (a type of loop) – For sufficiently-long strings (≥ p = 2 v), a non-terminal will be a descendant of itself in the parse • Because the language resulting from never reusing nonterminals is finite – leads to repetition properties, similar to loops in FAs • Every string of sufficient length from an infinite CFL can be written as uvxyz, and pumped as uvixyiz, which string is also in the same CFL – |x| > 0, |v| + |y| > 0, |vxy| <= p (= 2 v)

anbnan is not context-free • Intuitively: You’ve already used up the stack to coordinate the anbn prefix • Must consider all cases for a proof – CFLPL-8. PDF

ww is not Context Free • CFLPL-9. PDF

Closure Properties of CFLs • CFLs are closed under union, concatenation, and Kleene Star • CFLs are not closed under intersection or complement! • But the intersection of a CFL and a Regular language is a CFL

Union of CFLs • Let S 1 be the start symbol for L 1, and S 2 for L 2 • Just have a new start symbol point to the OR of the old ones: • S => S 1 | S 2 S 1 => … S 2 => …

Concatenation of CFLs • S => S 1 S 2 S 1 => … S 2 => …

Kleene Star of CFLs • Rename the old start non-terminal to S 1 • S => S 1 S | Λ S 1 => …

Intersection of CFLs • • Let L 1 = anbnam Let L 2 = anbmam (The CFGs for the above are on page 385) L 1 ∩ L 2 = a nb na n – We already showed this is not context free

Complement of CFLs • Proof by contradiction, derived from the result of intersection, because: L 1 ∩ L 2 = (L 1' + L 2')' Since the intersection is not closed, but union is, then the complement cannot be.

Complements of DCFLs • These are closed under complement • Just invert the acceptability conditions, similar to FAs – String is in L' if either an accept state is not reached or the stack is not empty • So, you would think that DCFLs are also closed under intersection, but they’re not, because…

DCFLs not Closed under Union! • Consider: L 1 = {aibjck | i = j} L 2 = {aibjck | j = k} • Each of these is DCF – (Show this!) • The union is not! – It requires non-determinism – It’s CF, but not DCF

Another Interesting Fact • DCFLs always have an associated CFG that is unambiguous

Closure Properties of CFLs Summary • Closed under Union, Concatenation, Kleene Star • Not closed under intersection, complement • CFL ∩ Regular = CFL • DCFLs are closed under complement – But not union!

Decidability • Unanswerable questions • Answerable questions

Undecidable Questions • Do 2 arbitrary CFGs generate the same language? • Is a CFG ambiguous? • Is a given CFL’s complement also CF? • Is the intersection of 2 given CFLs CF? • Do 2 CFLs have a common word?

Decidable Questions • Does a CFG generate any words? – Substitute each “terminating production” (RHS is all terminals) throughout and see what happens • “back substitution method” • Example, page 405 • Is a non-terminal ever used? (p. 406 -408) • Is a CFL finite or infinite? (p. 408 -409)

CYK Algorithm • Answers the question: “Is this string accepted by this grammar? ” – A “dynamic programming” algorithm – Works backwards in stages • There are better ways of parsing – Take the compiler class to learn those