Push Down Automata PDA Pertemuan 11 Mahasiswa mampu

Push Down Automata (PDA) Pertemuan 11 Mahasiswa mampu menerapkan konsep & definisi mekanisme Kerja Push Down Automata (PDA)

Materi • Mekanisme Kerja Push Down Automata (PDA) • Push Down Automata (PDA) untuk suatu tata Bahasa Bebas Konteks

Mekanisme Kerja Push Down Automata (PDA) Agar dapat menggunakan model automata pada bahasa context free, maka diperlukan: 1. Sebuah stack atau memori push down yang dapat menyimpan sederetan simbol dengan panjang yang sebarang dan tak berhingga. 2. Selama proses pembacaan simbol pada stack, simbol teratas pada sebuah stack PDA memiliki kemungkinan sebagai berikut: Ø Stack tidak dapat diubah, atau Ø Simbol pada stack teratas akan dihapus (pop) dan digantikan dengan simbol yang lain (push).

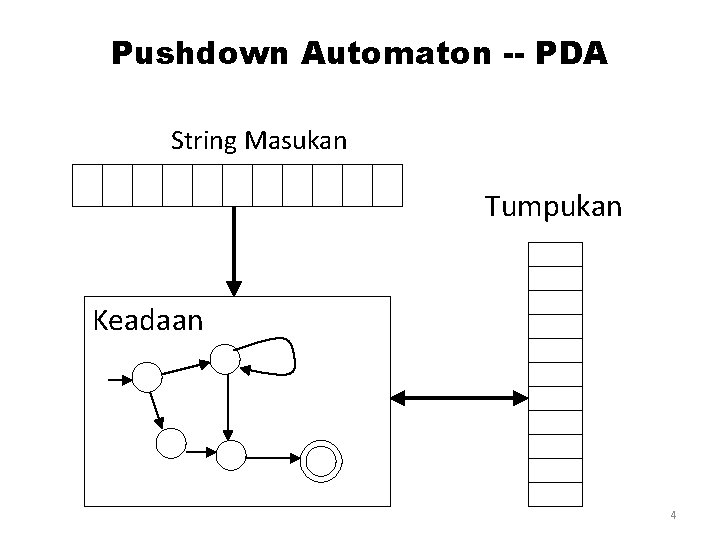
Pushdown Automaton -- PDA String Masukan Tumpukan Keadaan 4

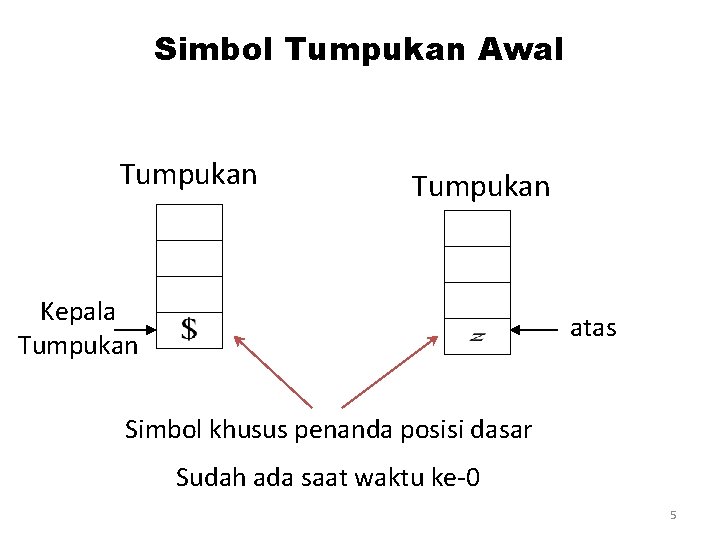
Simbol Tumpukan Awal Tumpukan Kepala Tumpukan atas Simbol khusus penanda posisi dasar Sudah ada saat waktu ke-0 5

7 tupel pada PDA M = (Q, ∑, Г, Δ, S, F, Z) Q = himpunan state ∑ = himpunan simbol input Г = simbol – simbol tumpukan / stack Δ = fungsi transisi S = state awal F = state akhir Z = simbol awal tumpukan

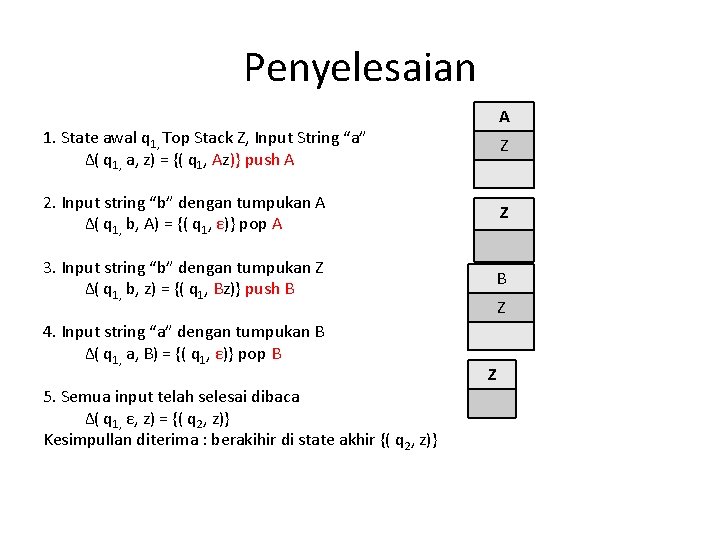
Penyelesaian A 1. State awal q 1, Top Stack Z, Input String “a” Δ( q 1, a, z) = {( q 1, Az)} push A Z 2. Input string “b” dengan tumpukan A Δ( q 1, b, A) = {( q 1, ε)} pop A Z 3. Input string “b” dengan tumpukan Z Δ( q 1, b, z) = {( q 1, Bz)} push B B 4. Input string “a” dengan tumpukan B Δ( q 1, a, B) = {( q 1, ε)} pop B 5. Semua input telah selesai dibaca Δ( q 1, ε, z) = {( q 2, z)} Kesimpullan diterima : berakihir di state akhir {( q 2, z)} Z Z

Push Down Automata (PDA) untuk suatu tata Bahasa Bebas Konteks Contoh : D → a. DA | b. Db | c Dapatkah menerima string “aca” Dapat dikontruksikan PDA- nya : 1. Terdapat 3 produksi : D → a. DA Fungsi transisi Г = { D, a, b, c, Z} : D → b. Db 1. Transisi D : D→c D → a. DA | b. Db | c Sehingga ada 3 state, maka : Δ( q 0, ε, z) = {( q 1, Dz)} Q = {q 0, q 1, q 2} D → a. DA | b. Db | c S = q 0 Δ( q 1, ε, D) = {( q 1, a. Da)}, {( q 1, b. Db)}, {( q 1, c)} 3. Transisi a, b, c F= {q 3 } Δ( q 1, a, a) = Δ( q 1, b, b)=Δ( q 1, c, c) = {( q 1, ε )} ∑ = {a, b, c} 4. Transisi Z Г = { D, a, b, c, Z} Δ( q 1, ε, z) = {( q 2, z)}

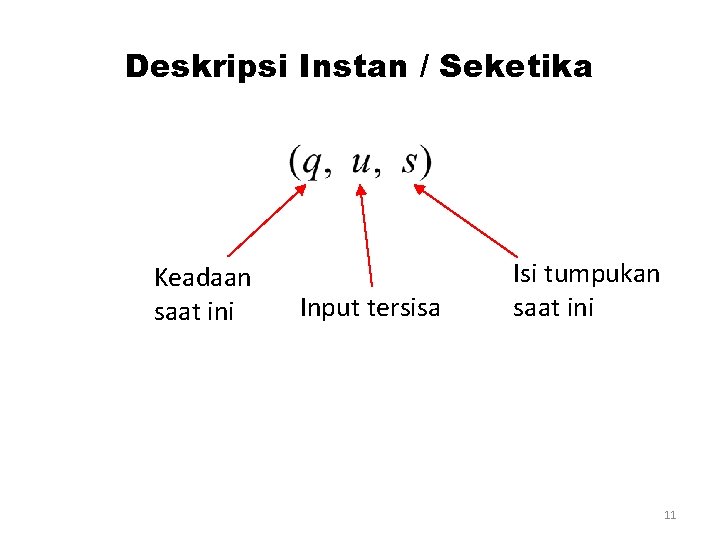
Deskripsi Instan / Seketika Keadaan saat ini Input tersisa Isi tumpukan saat ini 11

deskripsi seketika untuk string “aca” ( q 0, aca, z) |- ( q 1, aca, Dz) |- ( q 1, aca, a. Daz) |- ( q 1, ca, caz) |- ( q 1, a, az) |- ( q 1, ε, z) |- ( q 2, ε, z)

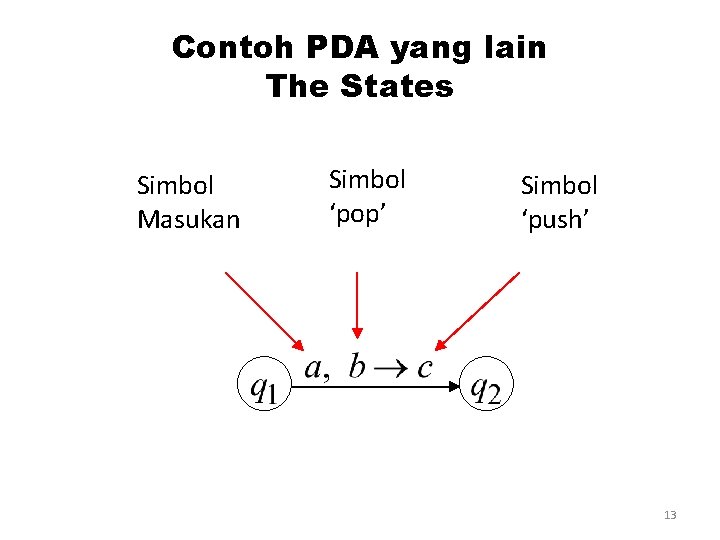
Contoh PDA yang lain The States Simbol Masukan Simbol ‘pop’ Simbol ‘push’ 13

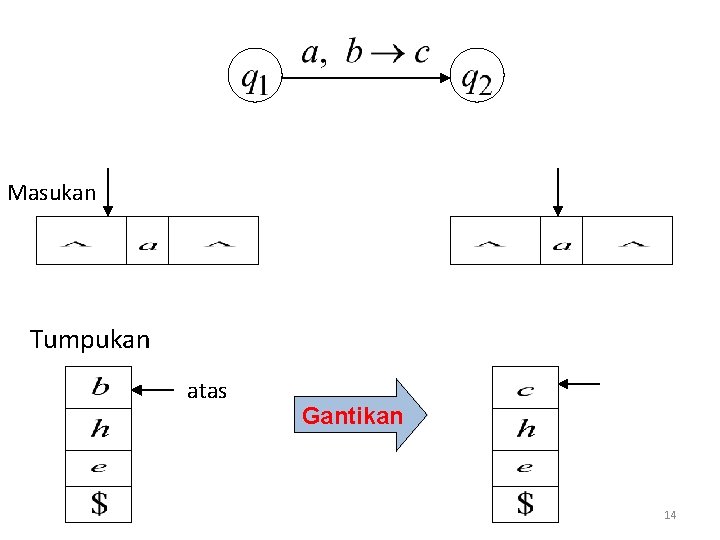
Masukan Tumpukan atas Gantikan 14

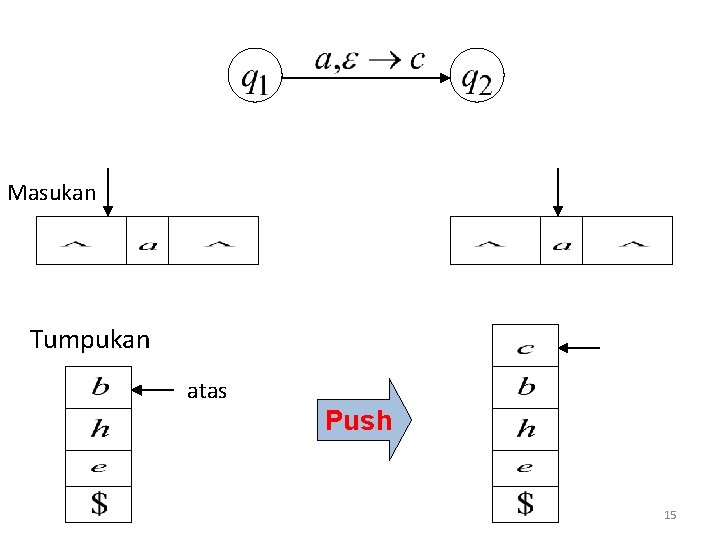
Masukan Tumpukan atas Push 15

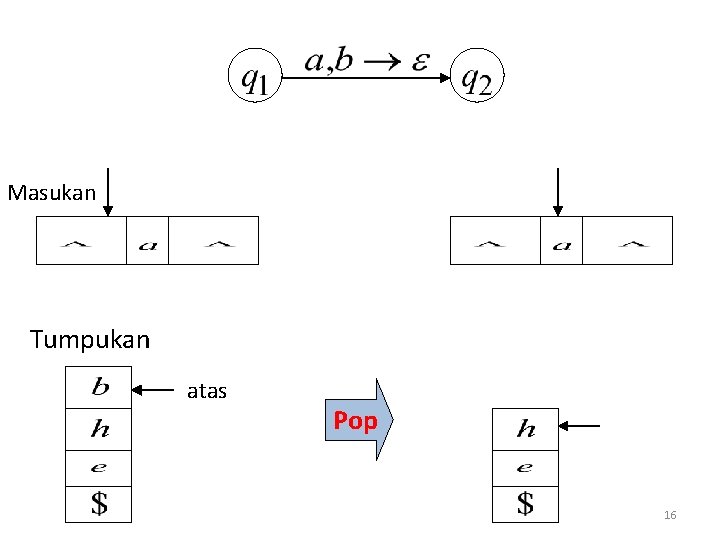
Masukan Tumpukan atas Pop 16

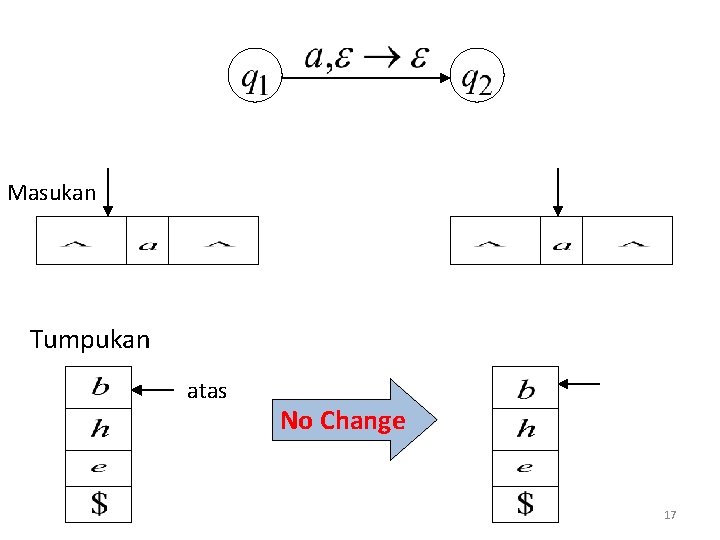
Masukan Tumpukan atas No Change 17

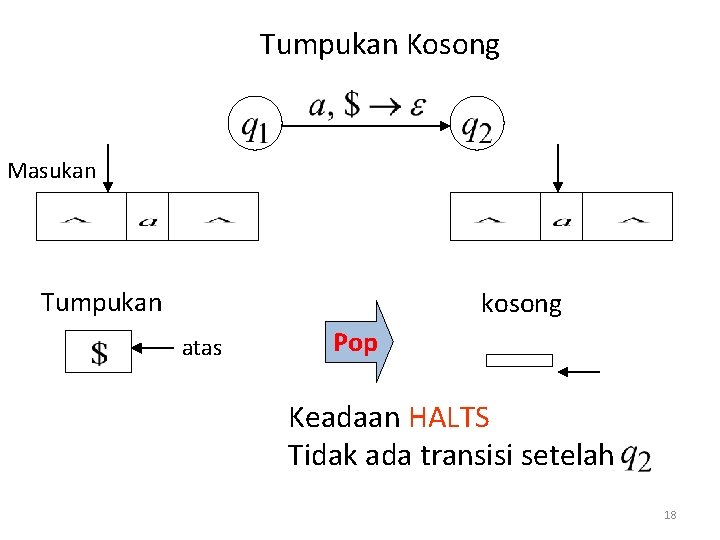
Tumpukan Kosong Masukan Tumpukan kosong atas Pop Keadaan HALTS Tidak ada transisi setelah 18

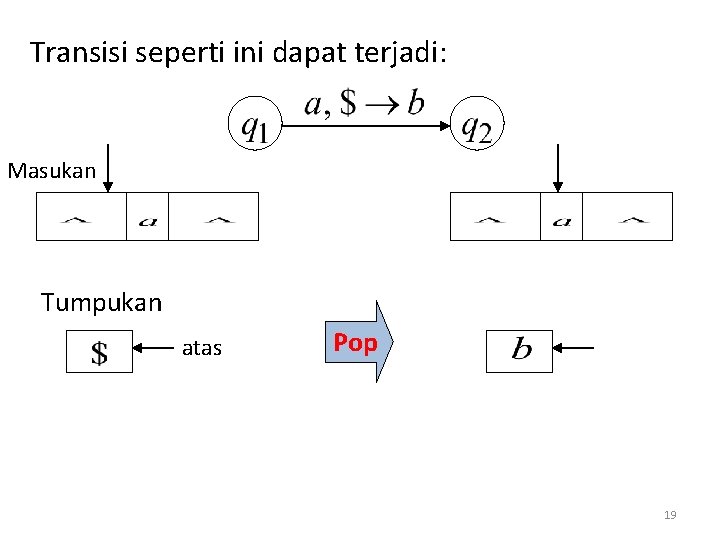
Transisi seperti ini dapat terjadi: Masukan Tumpukan atas Pop 19

Non-Deterministik PDA adalah non-deterministik 20

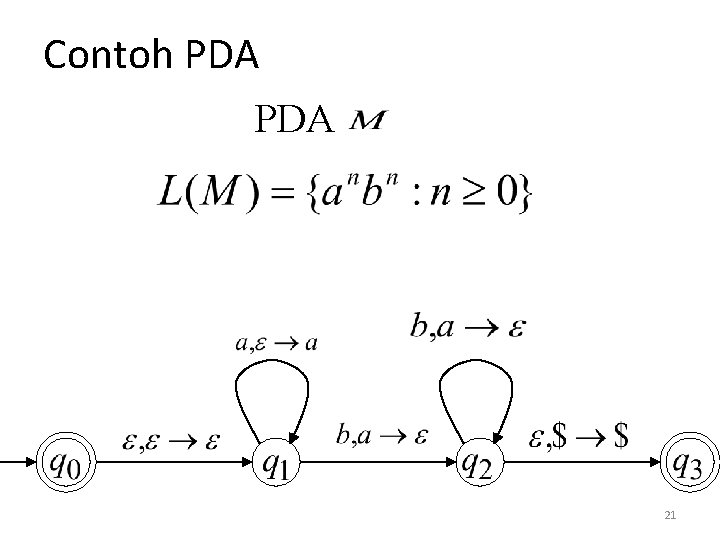
Contoh PDA 21

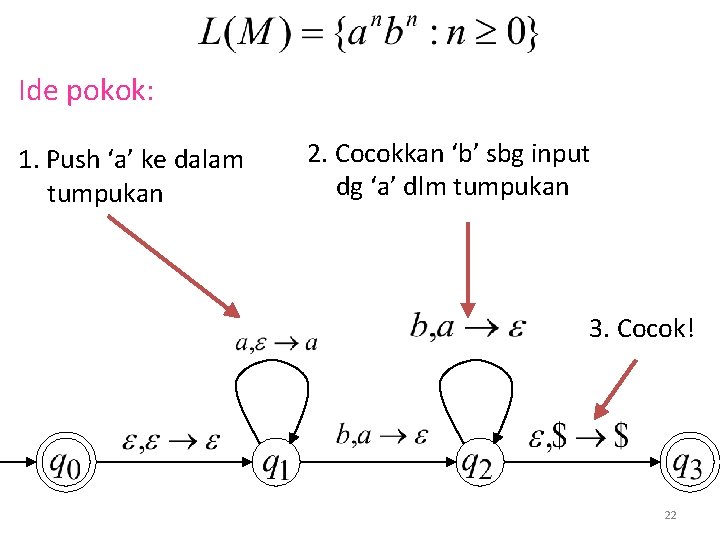
Ide pokok: 1. Push ‘a’ ke dalam tumpukan 2. Cocokkan ‘b’ sbg input dg ‘a’ dlm tumpukan 3. Cocok! 22

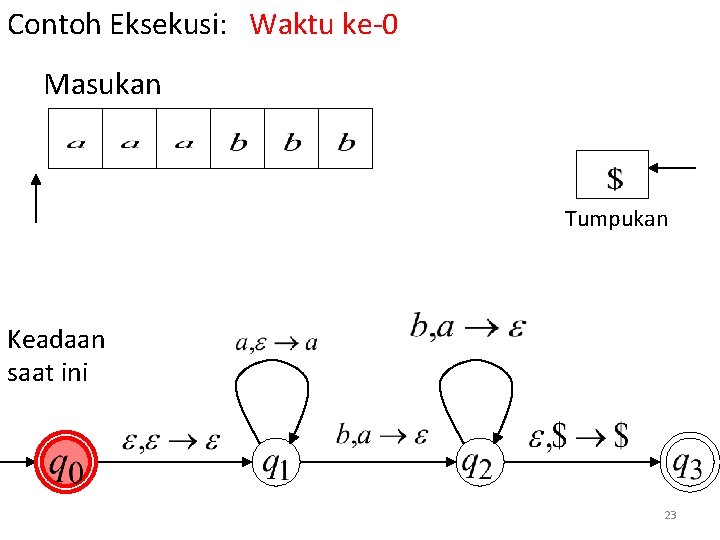
Contoh Eksekusi: Waktu ke-0 Masukan Tumpukan Keadaan saat ini 23

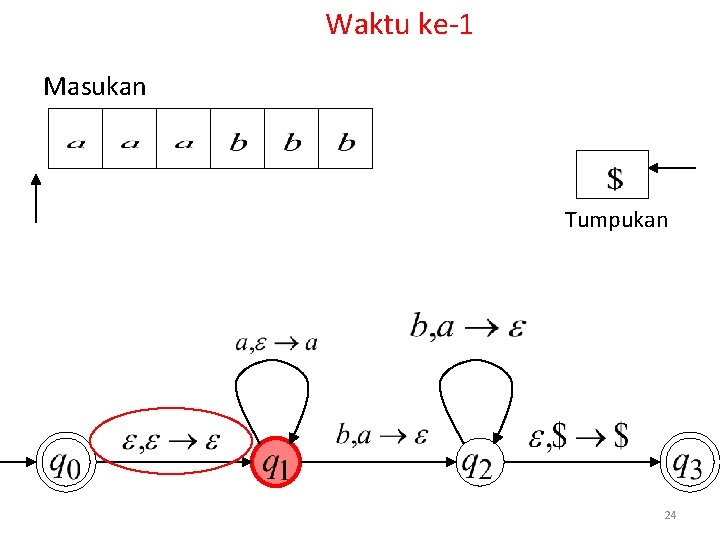
Waktu ke-1 Masukan Tumpukan 24

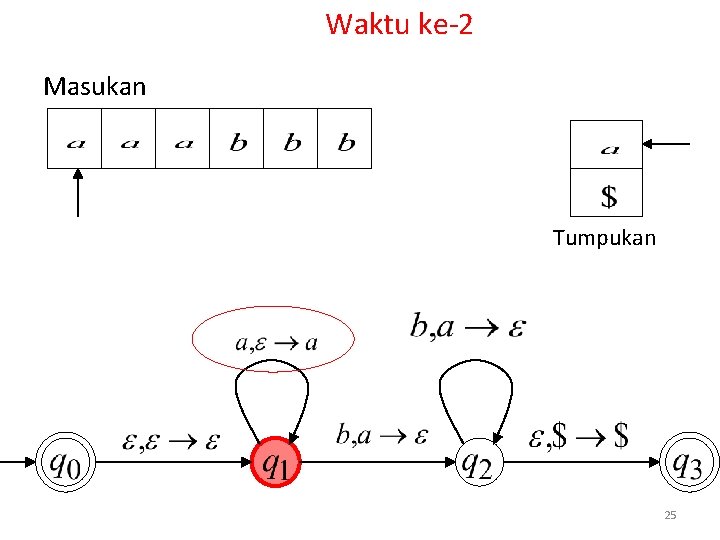
Waktu ke-2 Masukan Tumpukan 25

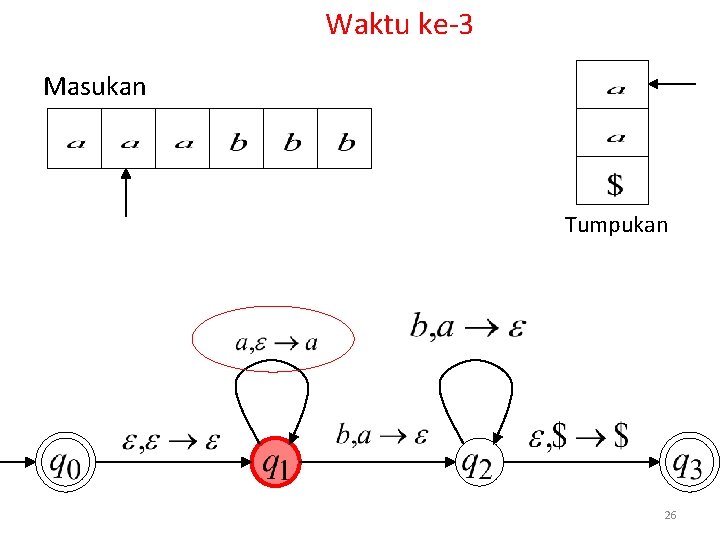
Waktu ke-3 Masukan Tumpukan 26

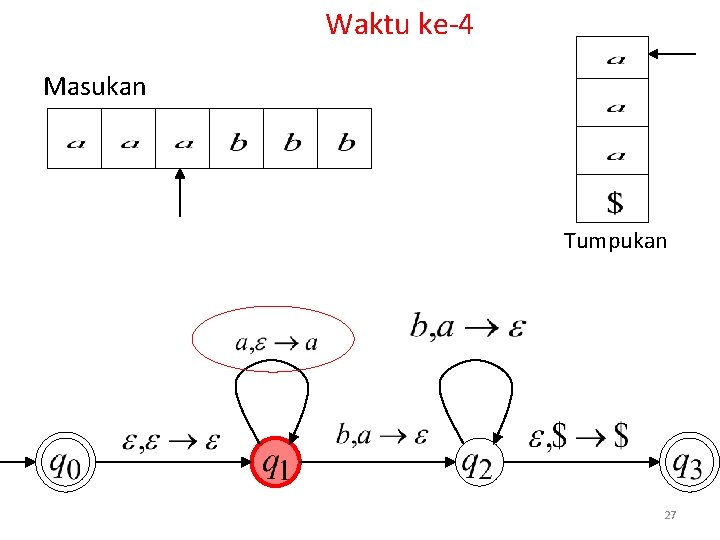
Waktu ke-4 Masukan Tumpukan 27

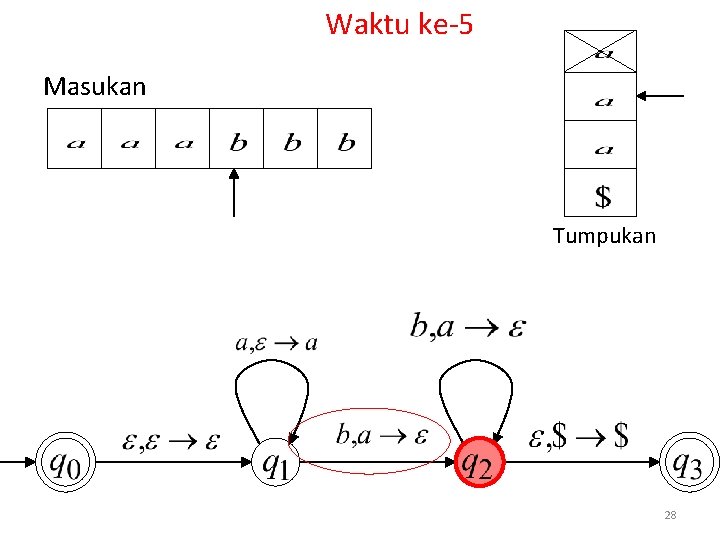
Waktu ke-5 Masukan Tumpukan 28

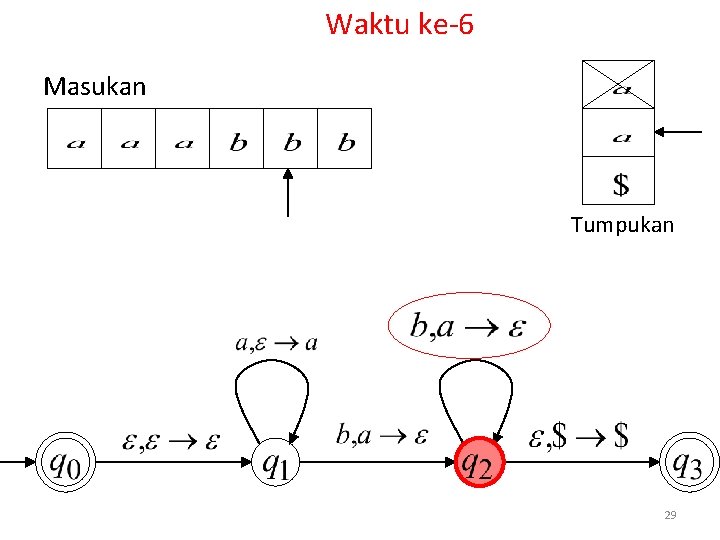
Waktu ke-6 Masukan Tumpukan 29

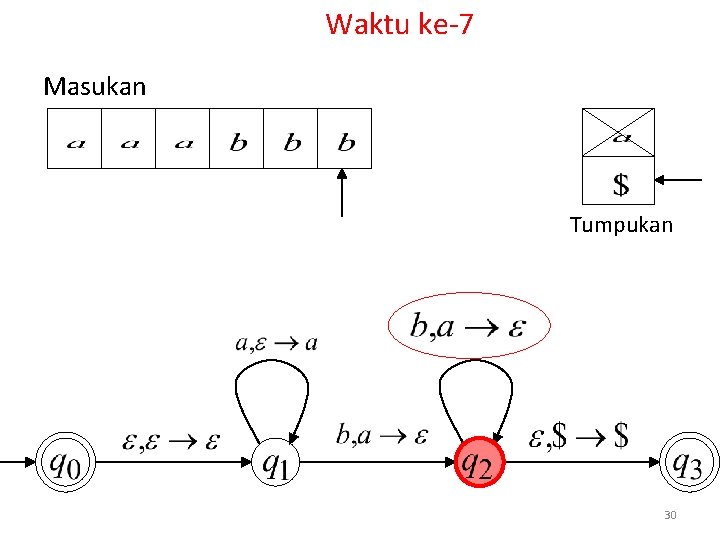
Waktu ke-7 Masukan Tumpukan 30

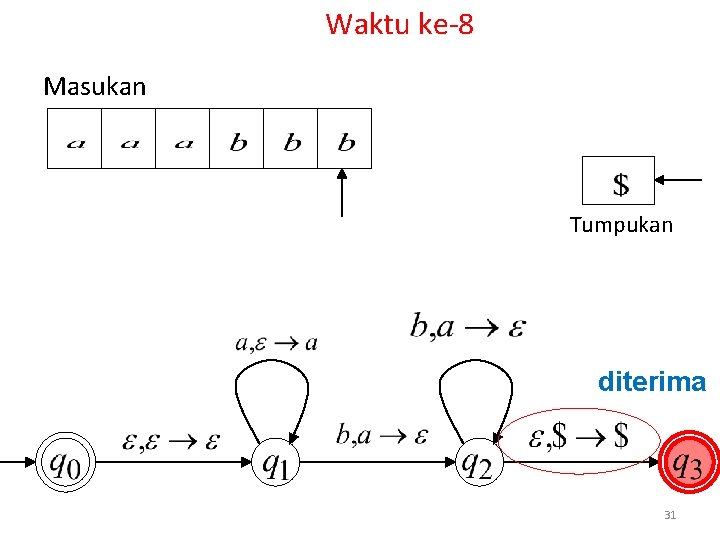
Waktu ke-8 Masukan Tumpukan diterima 31

Suatu string diterima jika: Semua Masukan selesai dieksekusi DAN Keadaan terakhir merupakan keadaan yang diterima Pada keadaan akhir, isi tumpukan tidak diperdulikan (isi tumpukan dapat kosong) 32