Purposeful Model Parameters Genesis in Simple Genetic Algorithms

Purposeful Model Parameters Genesis in Simple Genetic Algorithms Angelova M. , K. Atanassov, T. Pencheva maria. angelova@clbme. bas. bg, krat@bas. bg, tania. pencheva@clbme. bas. bg

Fermentation processes are: • characterized as complex, nonlinear, dynamic systems with interdependent and time-varying process variables; • described by non-linear models with a very complex structure. That is why an important step for adequate modeling of non-linear models of FP is the choice of a certain optimization procedure for model parameter identification. BIOMATH 2011, June 15 -18, Sofia, Bulgaria

Aims of the investigation • To improve the algorithm convergence time in standard simple genetic algorithm (SGA). • A stepwise procedure for purposeful genesis concerning intervals of variations of the model parameters to be proposed for a standard simple genetic algorithm aiming to improve significantly the algorithm effectiveness. • Such stepwise methodology to be applied to a parameter identification of a S. cerevisiae fed-batch cultivation. • Developed procedure to be further validated to a modified simple genetic algorithm with changed sequence of main genetic algorithm operators, namely mutation, crossover and selection. BIOMATH 2011, June 15 -18, Sofia, Bulgaria

Genetic algorithms (GA) : - are a direct random search technique for finding global optimal solution in complex multidimensional search space; - are based on mechanics of natural selection and natural genetics; - have advantages such as hard problems solving, noise tolerance, easy to interface and hybridize; - are proved to be very suitable for the optimization of highly non-linear problems, - are applied in the area of biotechnology, especially for parameter identification of fermentation process models. BIOMATH 2011, June 15 -18, Sofia, Bulgaria

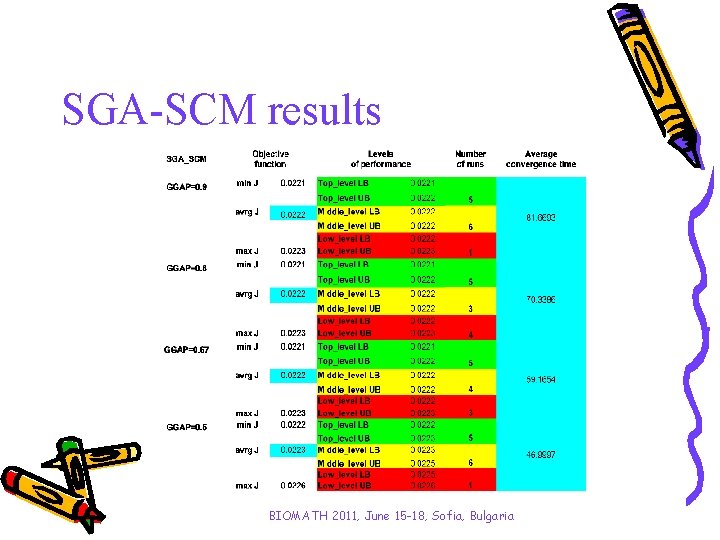
Investigated algorithms SGA-SCM and SGA-MCS SGA-SCM is the basic algorithm originally presented by Goldberg; SGA-MCS is elaborated in previous authors’ investigation where the results show that implementation of the main genetic operators in order mutation, crossover and selection significantly improves calculation time of the algorithm without affecting to the model adequacy. According to preliminary investigation of genetic algorithm’s parameters, the generation gap (GGAP - how many new individuals are created) is the most sensitive one towards to convergence time. Up to almost 40% from calculation time can be saved in cases of SGA-MCS application using GGAP = 0. 5 instead of 0. 9 without loss of model accuracy. BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-SCM - matlab code for generational loop % Create population Chrom = crtbp(NIND, NVAR*PRECI); % Counter gen = 0; % Evaluate Initial Population Obj. V = objfun(bs 2 rv(Chrom, Field. DR))'; % Iterate population while gen < MAXGEN, % Fitness assignement to whole population Fitn. V = ranking(Obj. V); % Select individuals from population Sel. Ch = select(‘rws’, Chrom, Fitn. V, GGAP); % Recombine selected individuals (crossover) Sel. Ch = recombin(‘xovdp’, Sel. Ch, 0. 85); % Mutate offspring Sel. Ch = mut(Sel. Ch, MUTR); % Evaluate Current Population Obj. VSel =objfun(bs 2 rv(Sel. Ch, Field. DR)); % Reinsert offspring in population replacing parents [Chrom Obj. V] = reins(Chrom, Sel. Ch, 1, 1, Obj. VSel'); % Increment counter gen = gen+1 end BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-MCS - matlab code for generational loop % Create population Chrom = crtbp(NIND, NVAR*PRECI); % Counter gen = 0; % Evaluate Initial Population Obj. V = objfun(bs 2 rv(Chrom, Field. DR))'; % Iterate population while gen < MAXGEN, % Mutate offspring New. Ch = mut(Chrom); % Recombine individuals (crossover) New. Ch = recombin(‘xovdp’, New. Ch, 0. 85); % Fitness assignement to whole population Fitn. V = ranking(New. CH); % Select individuals from population Sel. Ch = select(‘rws’, New. Ch, Fitn. V, GGAP); % Evaluate Current Population Obj. VSel =objfun(bs 2 rv(Sel. Ch, Field. DR)); % Reinsert offspring in population replacing parents [Chrom Obj. V] = reins(Chrom, Sel. Ch, 1, 1, Obj. VSel'); % Increment counter gen = gen+1 end BIOMATH 2011, June 15 -18, Sofia, Bulgaria

Mathematical model of S. cerevisiae fed-batch cultivation (1) – (5) where X, S, E, O 2 and O 2* are concentrations of biomass, substrate (glucose), ethanol, [g. l-1], oxygen and dissolved oxygen saturation, [%]; F – feeding rate, [l. h-1]; V – volume of bioreactor, [l]; – volumetric oxygen transfer coefficient, [h-1]; Sin – glucose concentration in the feeding solution, [g. l-1]; , q. S, q. E and are respectively specific rates of growth, substrate utilization, ethanol production and dissolved oxygen consumption, [h-1]. BIOMATH 2011, June 15 -18, Sofia, Bulgaria

Specific rates according to functional state modeling approach (6) where saturation constants of substrate and ethanol, [g. l-1]; Yij – yield coefficients, [g. g-1]. Optimization criterion: (7) where Y is the experimental data, Y* – model predicted data BIOMATH 2011, June 15 -18, Sofia, Bulgaria

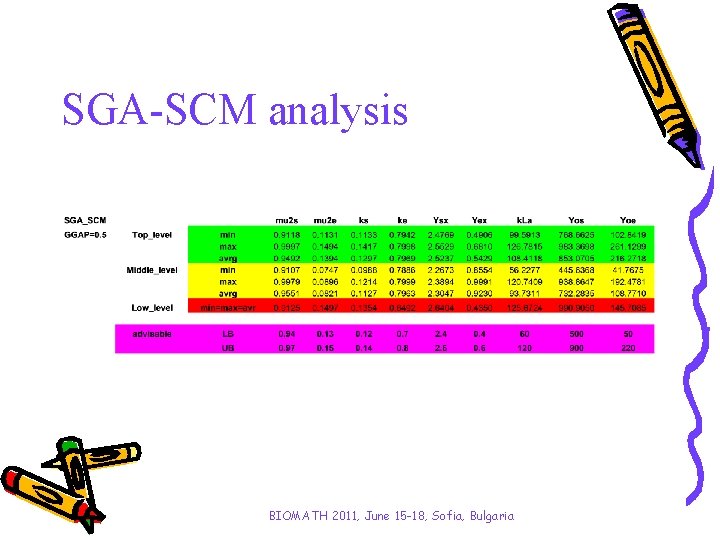
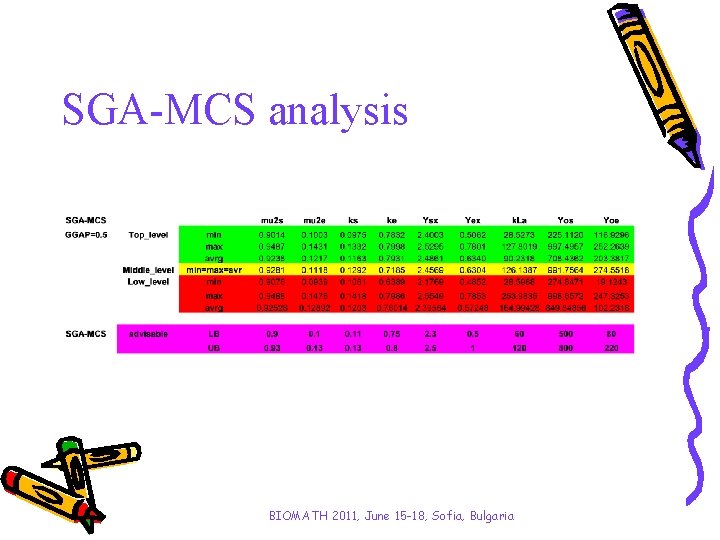
A procedure for purposeful genesis 1. Performing N runs of genetic algorithms 2. Determination of minimum and maximum of the objective function 3. Determination of top, middle and low level of performance with low boundary (LB) and up boundary (UB) following the scheme: Determination of discrimination number: Determination of top, middle and low level of performance with lower bound (LB) and upper bounds (UB) as follows Top_level: lower bound (TL_LB) min J upper bound (TL_UB) min J + ∆-ε Middle_level: lower bound (ML_LB) min J + ∆ upper bound (ML_UB) min J + 2∆-ε Low_level: lower bound (LL_LB) min J + 2∆ upper boundary (LL_UB) max J 4. Determination of parameters average values in each level 5. Based on averaged values, determination of new intervals of variations of model parameters 6. Run of genetic algorithm with new intervals BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-SCM results BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-SCM analysis BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-SCM analysis BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-MCS results BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-MCS analysis BIOMATH 2011, June 15 -18, Sofia, Bulgaria

SGA-MCS analysis BIOMATH 2011, June 15 -18, Sofia, Bulgaria

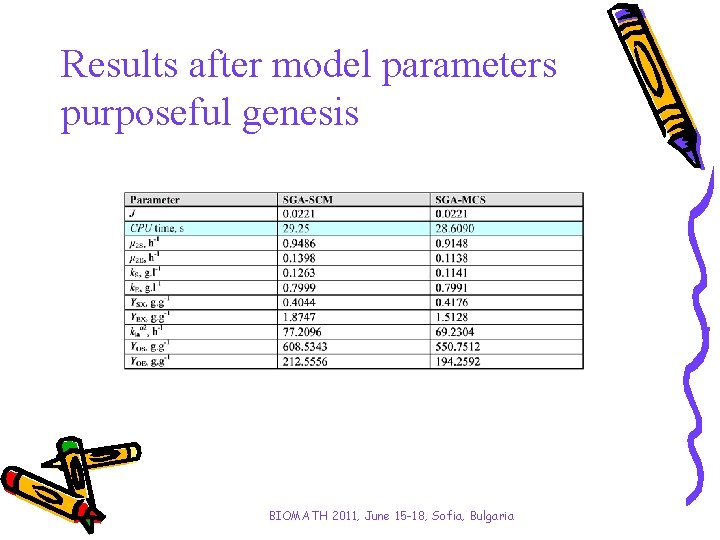
Results after model parameters purposeful genesis BIOMATH 2011, June 15 -18, Sofia, Bulgaria

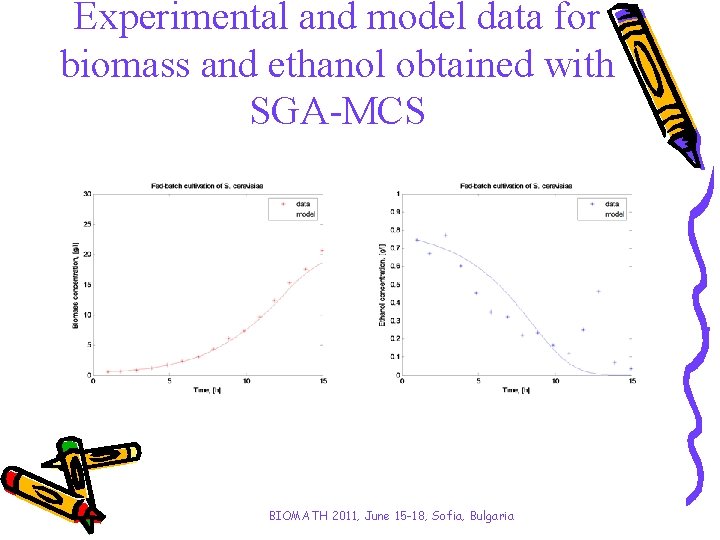
Experimental and model data for biomass and ethanol obtained with SGA-MCS BIOMATH 2011, June 15 -18, Sofia, Bulgaria

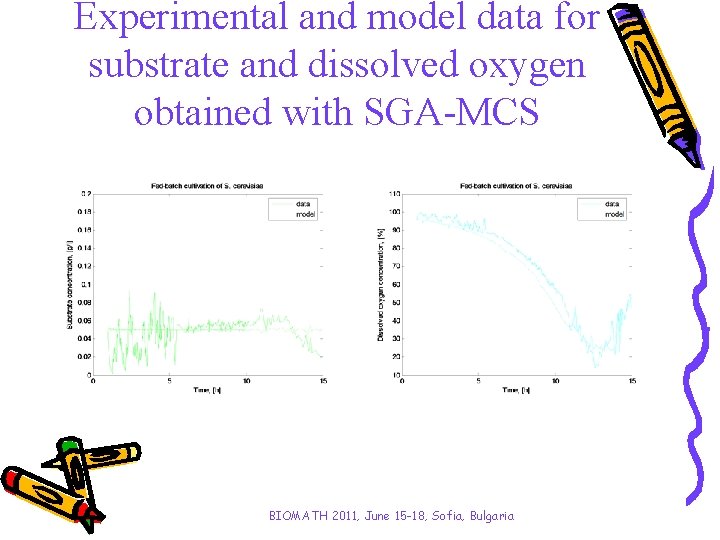
Experimental and model data for substrate and dissolved oxygen obtained with SGA-MCS BIOMATH 2011, June 15 -18, Sofia, Bulgaria

Analysis and conclusions • Two kinds of simple genetic algorithms have been investigated aiming to improve the algorithms convergence time. • A stepwise procedure for purposeful genesis concerning intervals of variations of model parameters is proposed for the algorithms. • When proposed stepwise parameter identification procedure has been applied the GA’s performance has been improved. - SGA-SCM has become with 38% faster; - SGA-MCS has achieved a solution 29% faster. • Results obtained with both applications SGA-SCM and SGA-MCS show significantly improvement of algorithm convergence time saving the model accuracy. BIOMATH 2011, June 15 -18, Sofia, Bulgaria

Acknowledgements This work is partially supported by the European Social Fund and Bulgarian Ministry of Education, Youth and Science under Operative Program “Human Resources Development”, grant BG 051 PO 001 -3. 3. 04/40 and National Scientific Fund of Bulgaria, grant number DID 02 -29. BIOMATH 2011, June 15 -18, Sofia, Bulgaria

Thank you for your attention BIOMATH 2011, June 15 -18, Sofia, Bulgaria