Pumpspeicherkraftwerk Einfhrung in die Integralrechnung Ulla Schmidt FreiherrvomSteinGymnasium

Pumpspeicherkraftwerk Einführung in die Integralrechnung Ulla Schmidt, Freiherr-vom-Stein-Gymnasium Lünen

Charakteristika n n n Realitätsnahes Problem Keine Flächenberechnung Bestimmung von Zufluss und Abfluss Von Anfang an negative Integrale Schwerpunkt auf dem Aspekt „Kumulation“ Verschiedene Modellbildungen möglich

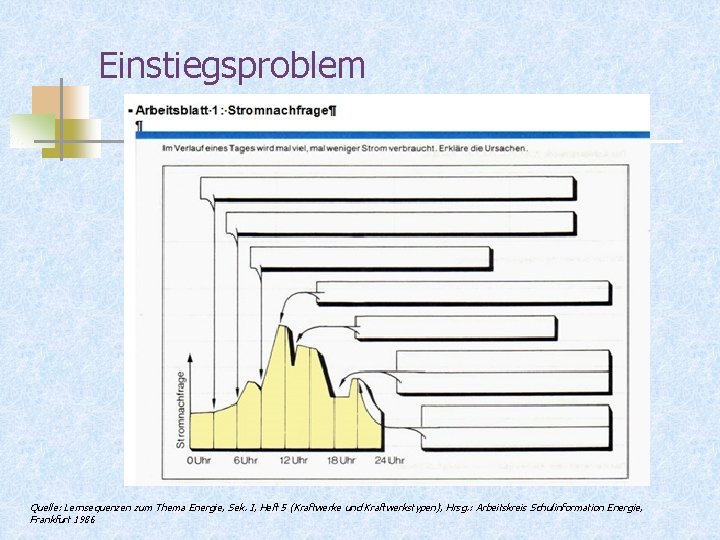
Einstiegsproblem Quelle: Lernsequenzen zum Thema Energie, Sek. I, Heft 5 (Kraftwerke und Kraftwerkstypen), Hrsg. : Arbeitskreis Schulinformation Energie, Frankfurt 1986

Problem n Nachts wird weniger Strom benötigt als tagsüber. n Man könnte mehr Strom produzieren als gebraucht wird. n Der Strom kann nicht gespeichert werden. Oder doch?

Pumpspeicherkraftwerk „Koepchenwerk Herdecke“ Informationsbroschüre der RWE Energie, Essen

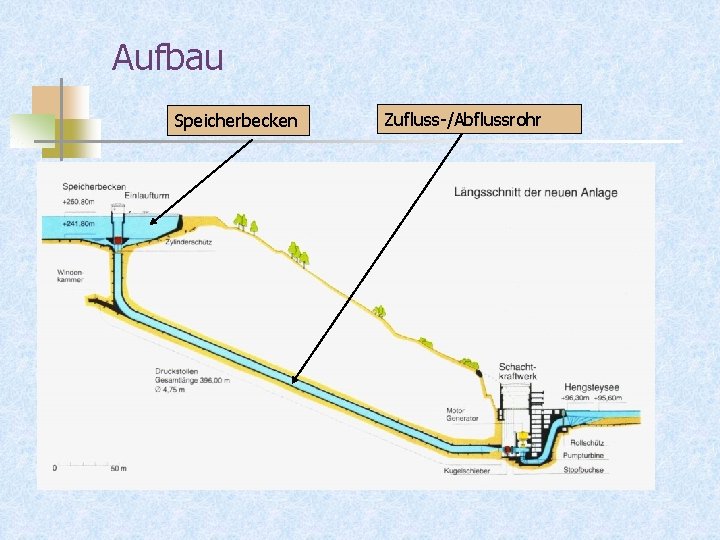
Aufbau Speicherbecken Zufluss-/Abflussrohr

1. Aufgabe n Skizziere die Wassermenge, die durch die Rohre fließt. Vereinbarungen: v Wassermengen, die nach oben gepumpt werden, werden positiv gezählt und Wassermengen, die nach unten abfließen, werden negativ gezählt.

Eine Schülerlösung … Zufluss-/Abflussrate Zeit t

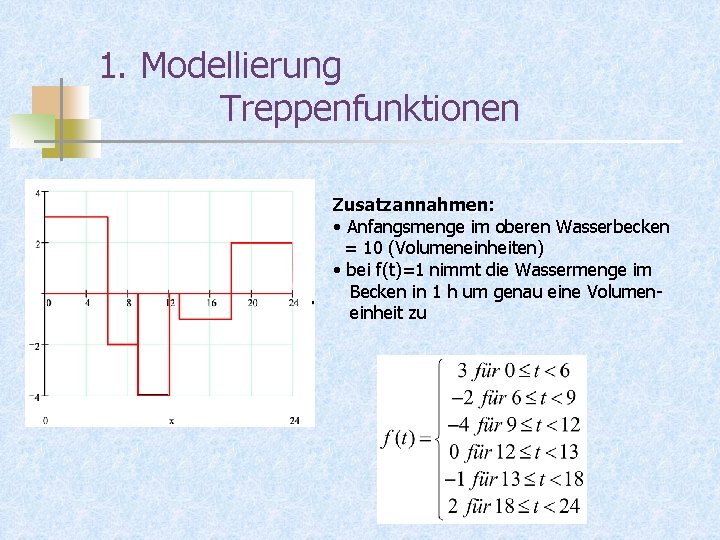
1. Modellierung Treppenfunktionen Zusatzannahmen: • Anfangsmenge im oberen Wasserbecken = 10 (Volumeneinheiten) • bei f(t)=1 nimmt die Wassermenge im Becken in 1 h um genau eine Volumeneinheit zu

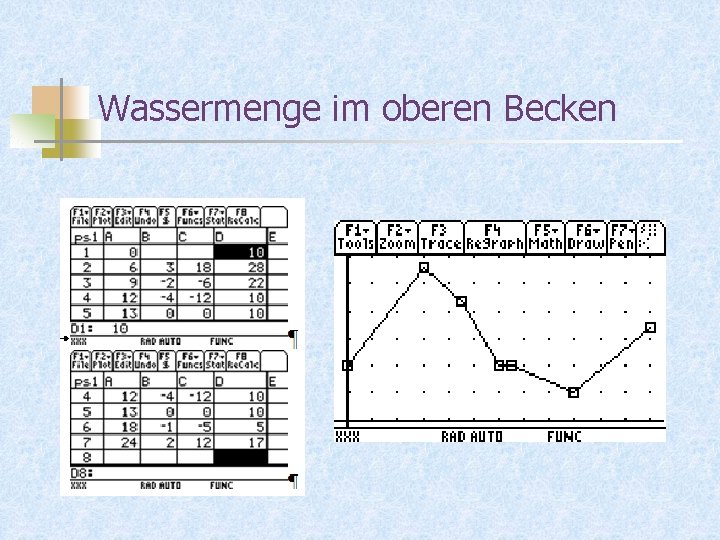
Aufgabe Ermittle die Wassermenge im oberen Becken zu den angegebenen Zeitpunkten. G Idee: Die pro Teilintervall zugeflossene Wassermenge lässt sich als vorzeichenbehafteter (orientierter) Flächeninhalt des Rechtecks zwischen Graph und x-Achse deuten.

Wassermenge im oberen Becken

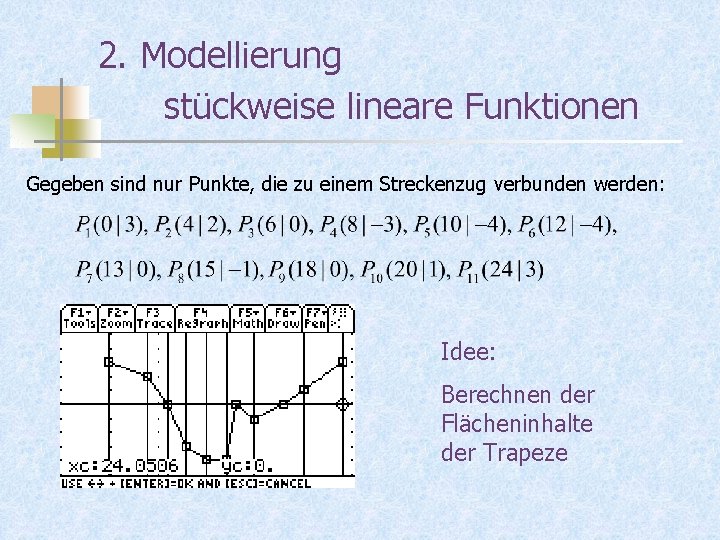
2. Modellierung stückweise lineare Funktionen Gegeben sind nur Punkte, die zu einem Streckenzug verbunden werden: Idee: Berechnen der Flächeninhalte der Trapeze

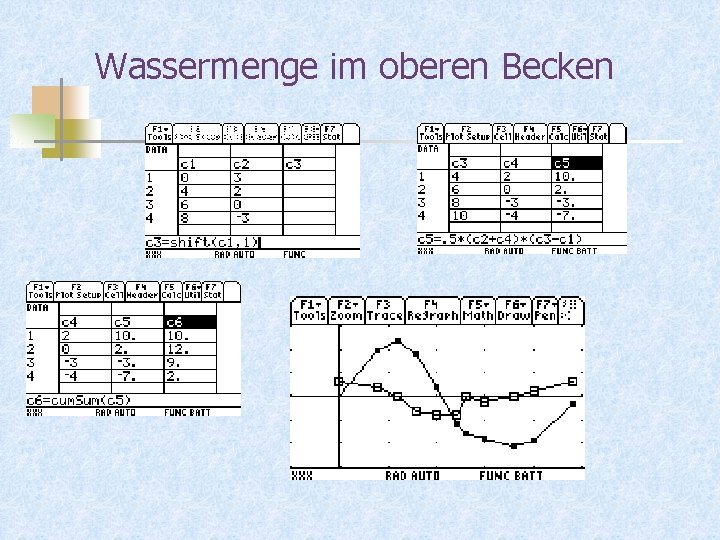
Wassermenge im oberen Becken

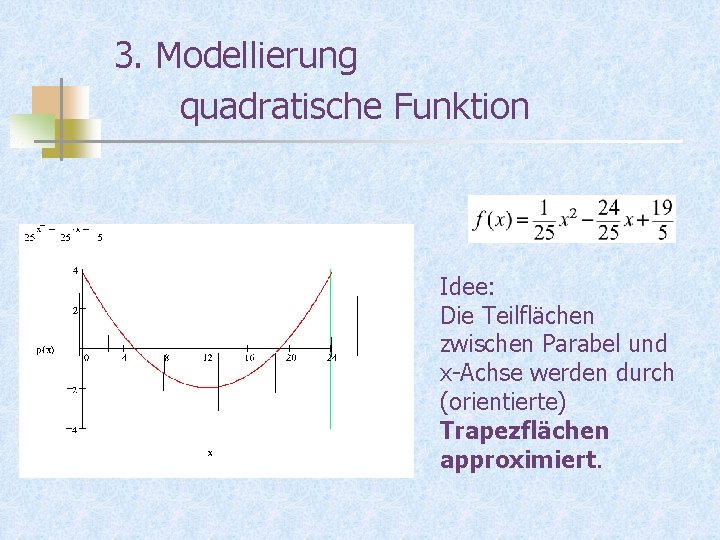
3. Modellierung quadratische Funktion Idee: Die Teilflächen zwischen Parabel und x-Achse werden durch (orientierte) Trapezflächen approximiert.

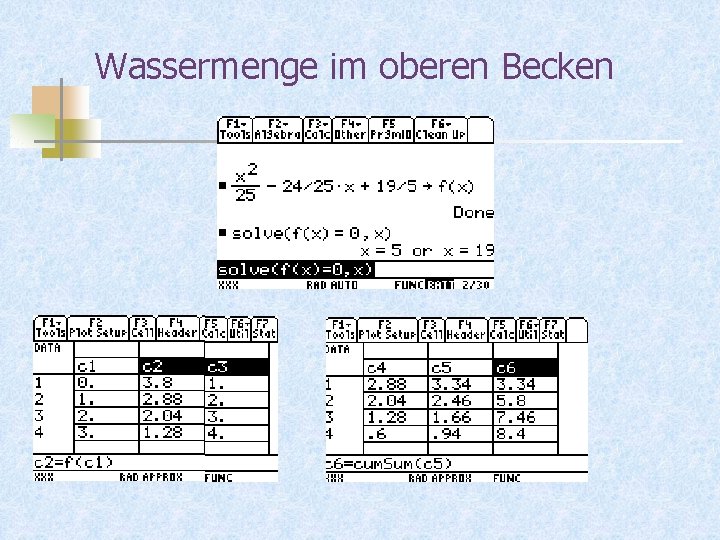
Wassermenge im oberen Becken

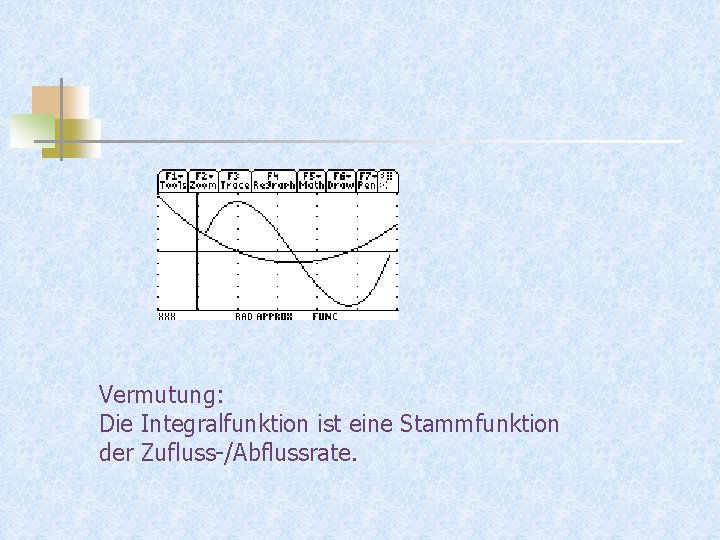
Vermutung: Die Integralfunktion ist eine Stammfunktion der Zufluss-/Abflussrate.

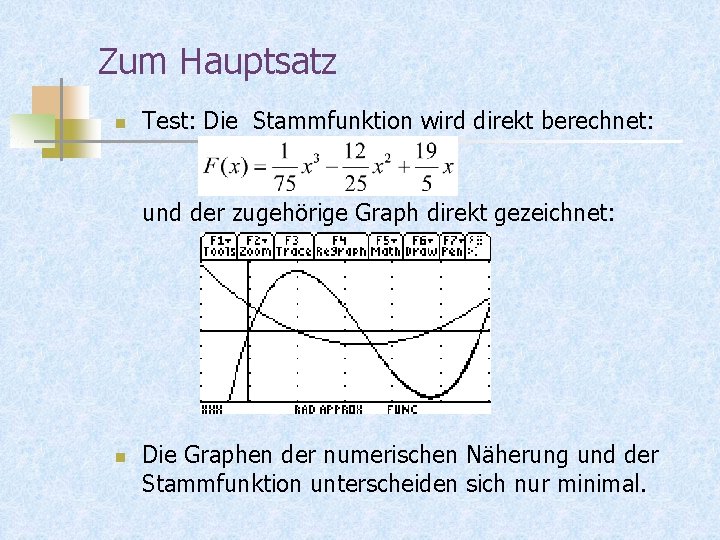
Zum Hauptsatz n Test: Die Stammfunktion wird direkt berechnet: und der zugehörige Graph direkt gezeichnet: n Die Graphen der numerischen Näherung und der Stammfunktion unterscheiden sich nur minimal.

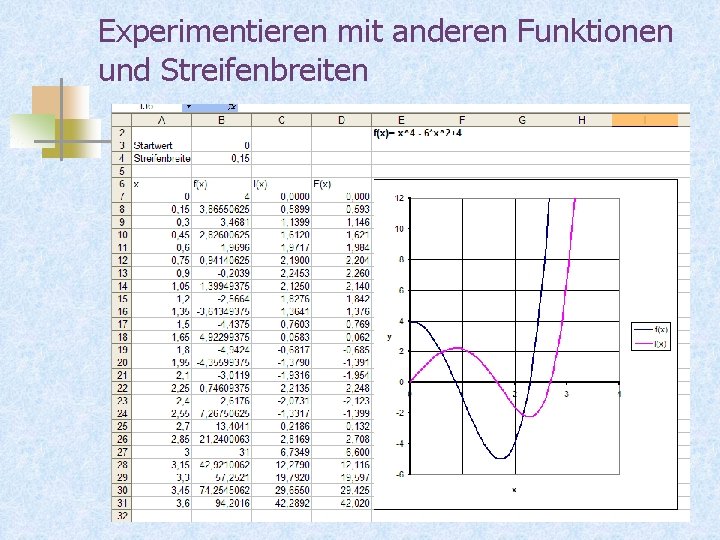
Experimentieren mit anderen Funktionen und Streifenbreiten