Pulsars and Gravitational Wave Detection George Hobbs ATNF

Pulsars and Gravitational Wave Detection George Hobbs (ATNF) 1 15 th April, 2004

Structure of talk n n n 2 Sources of detectable gravitational waves A review of the literature Work in progress 15 th April, 2004

What’s not in this talk … n n Description of pulsars (see e. g. books by Manchester or Lyne) Description of pulsar timing (see e. g. Backer & Hellings Ann. Rev. Astron. Astrophys. 1986. 24: 537) n Full details of models predicting gravitational waves (e. g. from cosmology) (see Maggiore ar. Xiv: grqc/9909001) n Detailed calculations (see e. g. Detweiler Ap. J 234: 1100 (1979), Foster & Backer Ap. J 361: 300 (1989), Jaffe & Backer Ap. J 583: 616 (2003) and Jenet et al. (in press)) 3 15 th April, 2004

Sources of ‘detectable’ GW n n n 4 Stochastic background left over as a cosmological remnant Highly relativistic neutron star or black hole binaries Impulse events of very short duration (e. g. supernova explosion) 15 th April, 2004

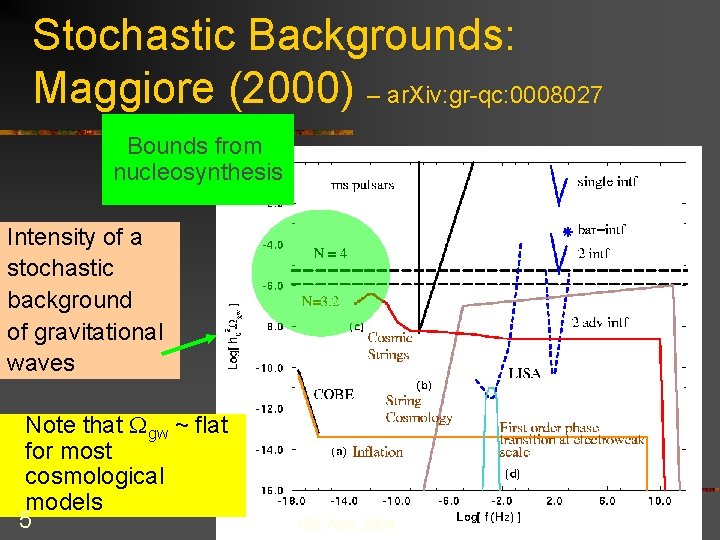
Stochastic Backgrounds: Maggiore (2000) – ar. Xiv: gr-qc: 0008027 Bounds from nucleosynthesis Intensity of a stochastic background of gravitational waves Note that Wgw ~ flat for most cosmological models 5 15 th April, 2004

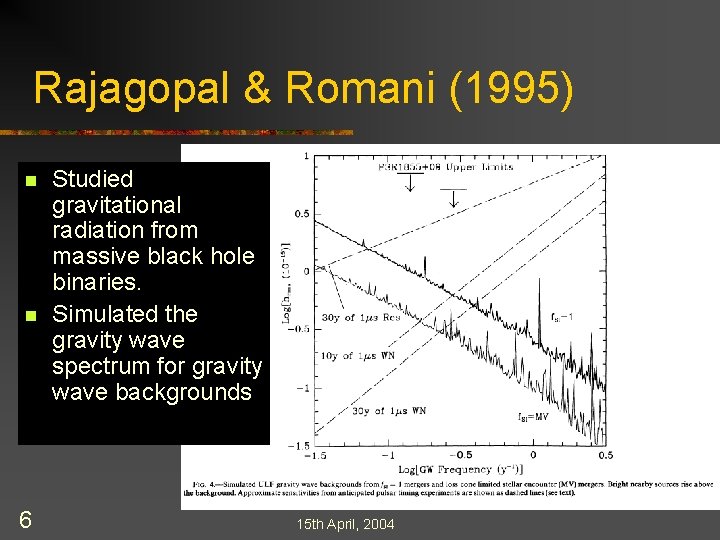
Rajagopal & Romani (1995) n n 6 Studied gravitational radiation from massive black hole binaries. Simulated the gravity wave spectrum for gravity wave backgrounds 15 th April, 2004

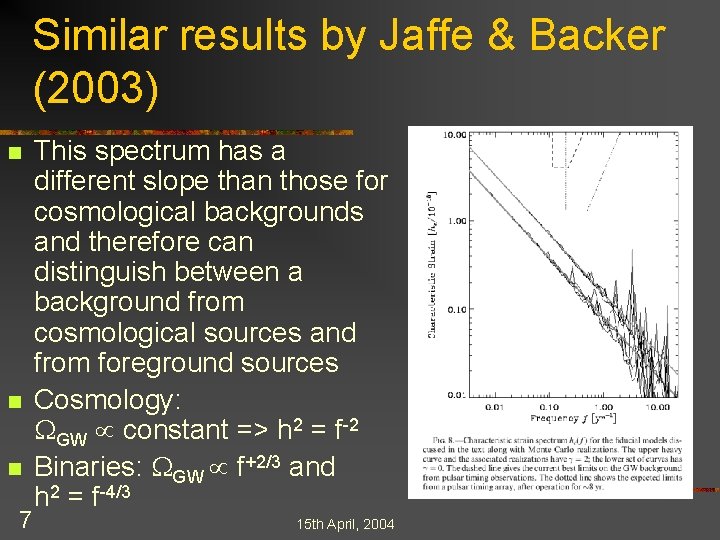
Similar results by Jaffe & Backer (2003) n n n 7 This spectrum has a different slope than those for cosmological backgrounds and therefore can distinguish between a background from cosmological sources and from foreground sources Cosmology: WGW constant => h 2 = f-2 Binaries: WGW f+2/3 and h 2 = f-4/3 15 th April, 2004

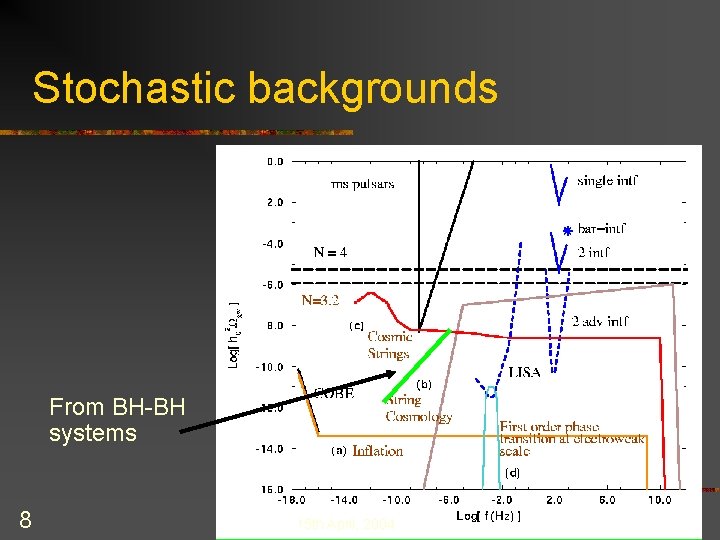
Stochastic backgrounds From BH-BH systems 8 15 th April, 2004

Pulsars n n n 9 Millisecond pulsars are a source of high precision measurements E. g. the period of B 1937+21 after 9 years of data: 1. 557 806 468 819 794 5 ± 0. 000 000 000 4 s This stability makes pulsars competitive with atomic clocks on long timescales 15 th April, 2004

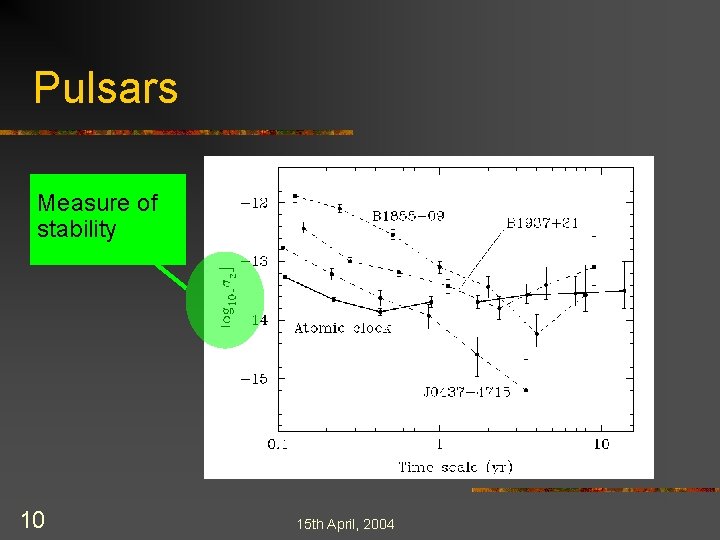
Pulsars Measure of stability 10 15 th April, 2004

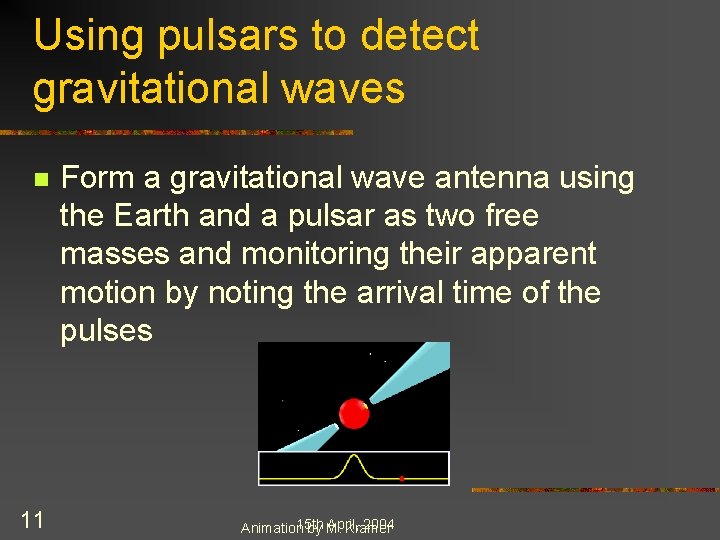
Using pulsars to detect gravitational waves n 11 Form a gravitational wave antenna using the Earth and a pulsar as two free masses and monitoring their apparent motion by noting the arrival time of the pulses 15 th April, 2004 Animation by M. Kramer

Detection methods … n n 12 Measur e of the amplitude of the GW Data from any pulsar contain information about h(t) at Earth and h(t) at the pulsar at the time of the emission of the pulse. The effect of a passing gravitational wave causes a change in the observed rotational frequency of a pulsar by an amount proportional to the amplitude of the wave 15 th April, 2004

Expected timing residuals R(t) = r/c + ½ cos(2 f)sin 2 q h(r’, t’)dr’/c 13 15 th April, 2004

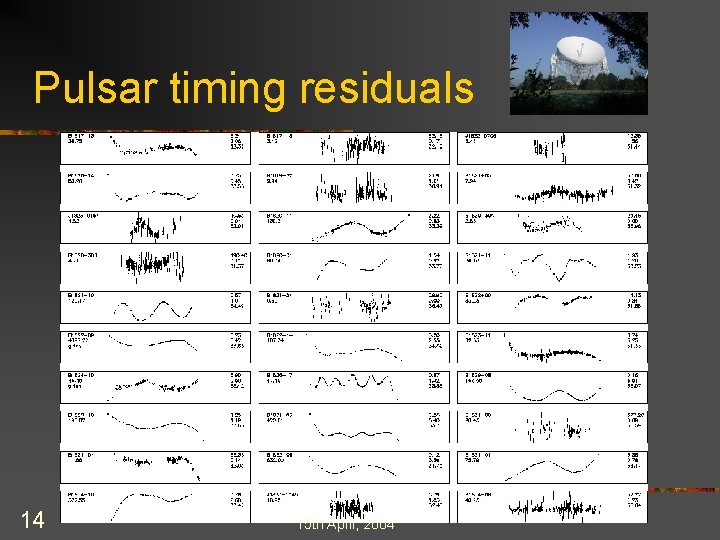
Pulsar timing residuals 14 15 th April, 2004

GW Frequencies ‘observable’ n. If the uncertainty in the time of arrival of a typical pulse is e and the total integration time is T then this ‘detector’ would be sensitive to gravitational wave amplitudes, h(f) ~ e/T for frequencies ~ 1/T. n. For a few years of integration have f ~ 10 -9 – 10 -8 Hz 15 15 th April, 2004

Detweiler (1979) n n 16 The characterisation of a gravitational wave coming from an unknown direction requires the monitoring of at least three pulsars that are not coplanar with the solar system (forward and backward directions of the wave cannot be distinguished). For a stochastic background, the mean square residual <R 2(t)> = 208/243 Gr/(p 3 f 4) where r is the effective energy density of a GW. 15 th April, 2004

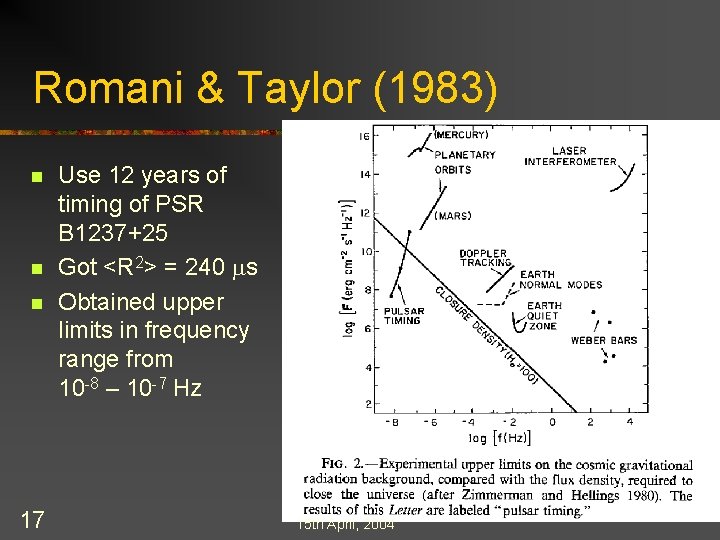
Romani & Taylor (1983) n n n 17 Use 12 years of timing of PSR B 1237+25 Got <R 2> = 240 ms Obtained upper limits in frequency range from 10 -8 – 10 -7 Hz 15 th April, 2004

Kaspi, Taylor & Ryba (1994) n n n 18 Studied PSRs B 1855+09 and B 1937+21 (~ 8 year time spans) Assumed that the power spectrum of pulsar timing residuals: Pgw(f) = H 2/(8 p 4)Wgwf-5 where Wgw = r/rc is the fractional energy density in GW per logarithmic frequency interval Get that Wgw h 2 < 6 x 10 -8 (95% confidence) 15 th April, 2004 P(f) f-a a = 0 (white noise) a = 2 -4 (clock instabilities, ephemeris errors, interstellar propagation effects, pulsar rotational instabilities a = 5 (gravitational wave background)

Lommen (2002) n n n 19 Have 17 years of data for PSRs B 1937+21 and B 1855+09. Obtain Wg h 2 < 2 x 10 -9 (an order of magnitude smaller than the Kaspi et al. result) Noted that J 0437 -4715 (5. 8 ms pulsar) which is very bright should be very good for timing 15 th April, 2004

Lommen & Backer (2001) n Attempted to detect Sag A* as a binary black hole system using residuals from PSRs J 1713+0747, B 1855+09 and B 1937+21. Calculated an expected periodicity in timing residuals with amplitude ~10 ns (not detectable yet!) If we can reach a timing precision of 100 ns then we can put meaningful constraints on ~10 nearby sources 20 15 th April, 2004

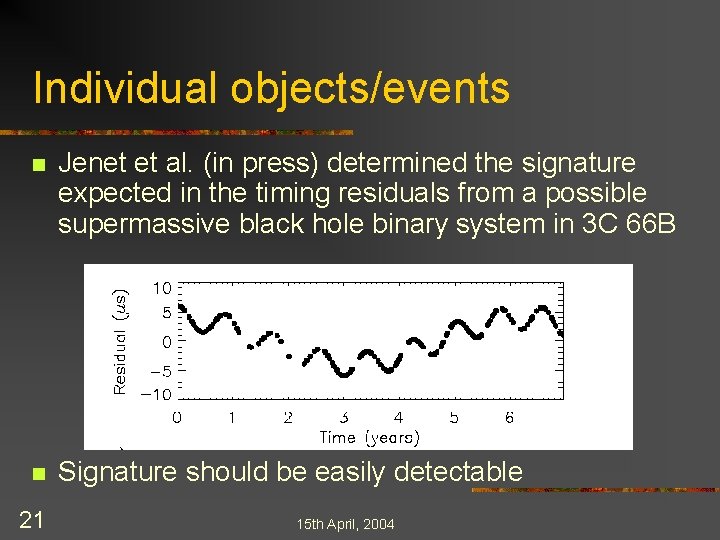
Individual objects/events n Jenet et al. (in press) determined the signature expected in the timing residuals from a possible supermassive black hole binary system in 3 C 66 B n Signature should be easily detectable 21 15 th April, 2004

Using multiple pulsars Problems when attempting to detect gravitational waves from pulsar timing data: n n n 22 Pulsars have intrinsic timing noise Primary terrestrial time standards fluctuate – effects all pulsars equally (monopole effect) Ephemeris errors in the transformation to the solar system barycentre (dipole effect) 15 th April, 2004

n. Image Monopole 23 15 th April, 2004 from Manchester talk

n. Image Dipole 24 15 th April, 2004 from Manchester talk

n. Image Quadrupole 25 15 th April, 2004 from Manchester talk

Multiple pulsars: Helling & Downs (1983) n n 26 Data from any pulsar will have a gravitational wave signal in common with all other pulsars (scaling propotional to the angle between the line-of-sight to the pulsar and the propagation direction of the GW) as well as a component which will be independent of the others. Cross-correlate data from several pulsars to obtain this common signal. 15 th April, 2004

Foster & Backer (1990) n n n 27 An effective pulsar timing array requires a minimum of 5 pulsars widely separated on the sky. Two observing frequencies required to remove dispersion measure variations. Three pulsars required for ephemeris terms, one pulsar to act as a clock and one to provide a limit on the amplitude of the GW background. 15 th April, 2004

Our Pulsar Timing Array n n 28 Use the Parkes radio telescope to observe millisecond pulsars for 5+ years with ~weekly observations. Intend to work hard with RFI mitigation etc. to obtain the highest precision TOAs possible. Collaborate with observers in the Northern hemisphere to obtain a large sample of pulsars across the sky 15 th April, 2004

Distribution of msps on the sky n. All except two millisecond pulsars are observable from Parkes! 29 15 th April, 2004

Observing n. We are currently observing 32 pulsars using the Parkes telescope using the dual-frequency 10 -50 cm receiver (with extra observations at 20 cm and 3 cm). n. We are obtaining pulse arrival times with uncertainties of 0. 2 ms for PSR J 0437 -4715 at 10 cm and 4 ms at 20 cm (using correlator) - van Straten et al. (2001) obtained ~80 ns timing residuals! n. For PSR J 1909 -3744 we are getting uncertainties of ~1. 5 ms (using correlator) n. This 30 is without much RFI mitigation etc. 15 th April, 2004

Super. Tempo n 31 Have computer code that can fit individual pulsar parameters and global parameters to multiple pulsar data sets simultaneously. 15 th April, 2004

Conclusions n n n 32 Pulsar timing provides the opportunity for detecting gravitational waves with periods ~year. So far, limits have been placed on the stochastic gravitational wave background and limits have been placed on black hole binary systems Our timing array project will contain more observations of more pulsars at more frequencies to obtain higher timing precision than has been obtained by any previous study … 15 th April, 2004