PTT 205 HEAT MASS TRANSFER SEM II 20162017

PTT 205 HEAT & MASS TRANSFER SEM II (2016/2017) EMPIRICAL RELATIONS OF CONVECTIVE HEAT TRANSFER & FREE CONVECTION CO 1: Ability to apply the basic principles and to calculate different modes of heat transfer

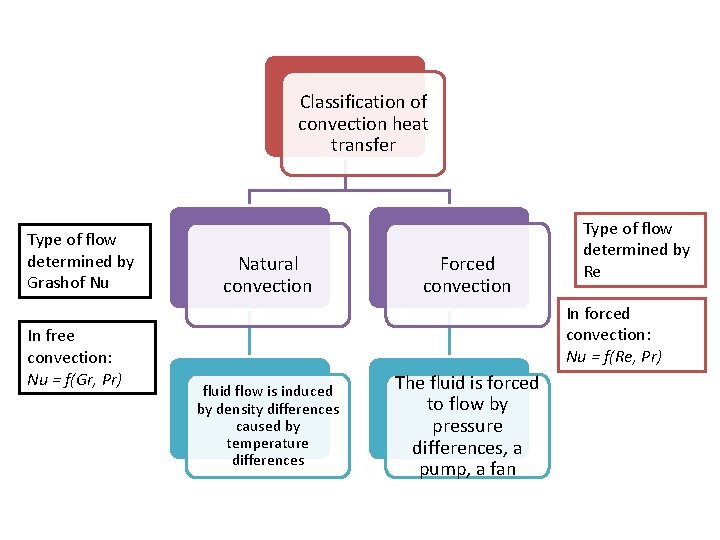
Classification of convection heat transfer Type of flow determined by Grashof Nu In free convection: Nu = f(Gr, Pr) Natural convection Forced convection Type of flow determined by Re In forced convection: Nu = f(Re, Pr) fluid flow is induced by density differences caused by temperature differences The fluid is forced to flow by pressure differences, a pump, a fan

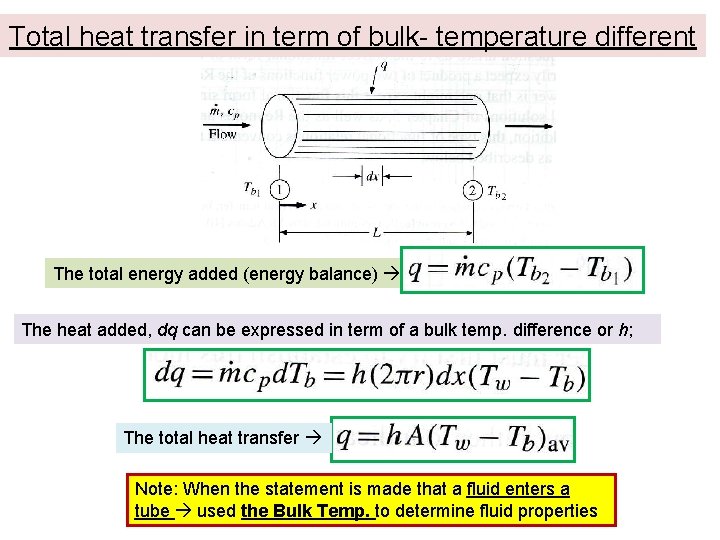
Total heat transfer in term of bulk- temperature different The total energy added (energy balance) The heat added, dq can be expressed in term of a bulk temp. difference or h; The total heat transfer Note: When the statement is made that a fluid enters a tube used the Bulk Temp. to determine fluid properties

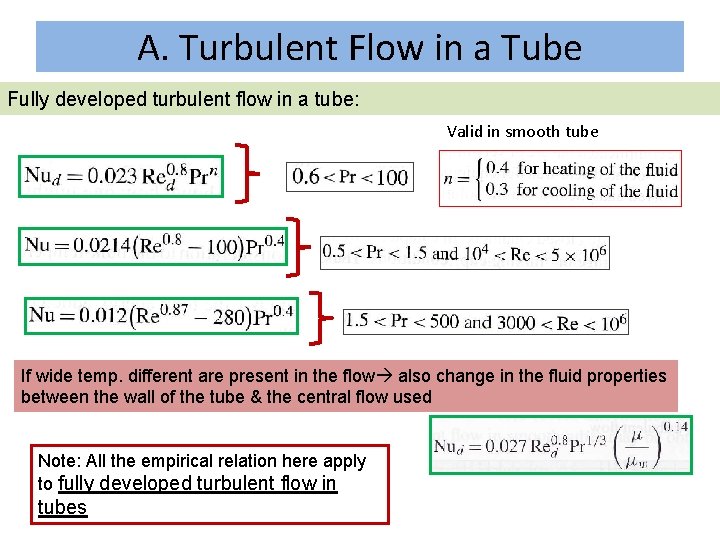
A. Turbulent Flow in a Tube Fully developed turbulent flow in a tube: Valid in smooth tube If wide temp. different are present in the flow also change in the fluid properties between the wall of the tube & the central flow used Note: All the empirical relation here apply to fully developed turbulent flow in tubes

A. Turbulent Flow in a Tube For the entrance region and for short tubes (The flow is not developed), used: Thermal properties at bulk temperature.

More accurate although more complicated, the expression for fully developed turbulent flow in smooth tube is; or All the properties using in this equation based on Tf

Example 1: Turbulent Heat Transfer in a Tube Air at 2 atm and 200 °C is heated as it flows through a tube with a diameter on 1 in (2. 54 cm) at a velocity of 10 m/s. a) Calculate the heat transfer per unit length of tube if a constant-heat-flux condition is maintained at the wall and the wall temp. is 20 °C above the air temp. , all along the length of the tube. b) How much would the bulk temp. increase over a 3 m length of the tube?

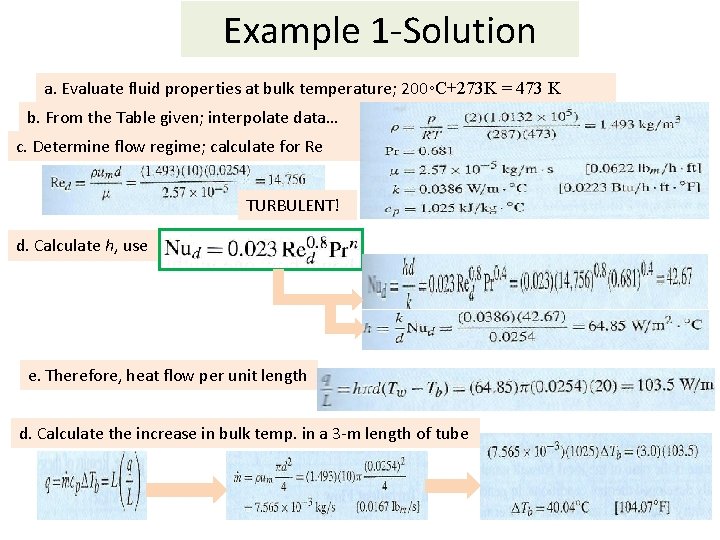
Example 1 -Solution a. Evaluate fluid properties at bulk temperature; 200◦C+273 K = 473 K b. From the Table given; interpolate data… c. Determine flow regime; calculate for Re TURBULENT! d. Calculate h, use e. Therefore, heat flow per unit length d. Calculate the increase in bulk temp. in a 3 -m length of tube

Example 2: Heat Transfer (Turbulent Flow) in a Rough Tube A 2. 0 cm diameter tube having a relative roughness of 0. 001 is maintained at a constant wall temp. of 90 °C. Water enters the tube at 40 °C and leaves at 60 °C. if the entering velocity is 3 m/s, calculate the length of tube necessary to accomplish the heating.

Example 2 -Solution a. Calculate heat transfer; b. Since the tube has relative roughness apply c. Evaluate water properties at film temperature d. From the Table e. Compute for Re. no. f. Find friction factor, f-value from Graph 6. 4: g. Since Tw > Tb, n = 0. 11 h. Calculate length of the tube from energy balance Turbulent!!

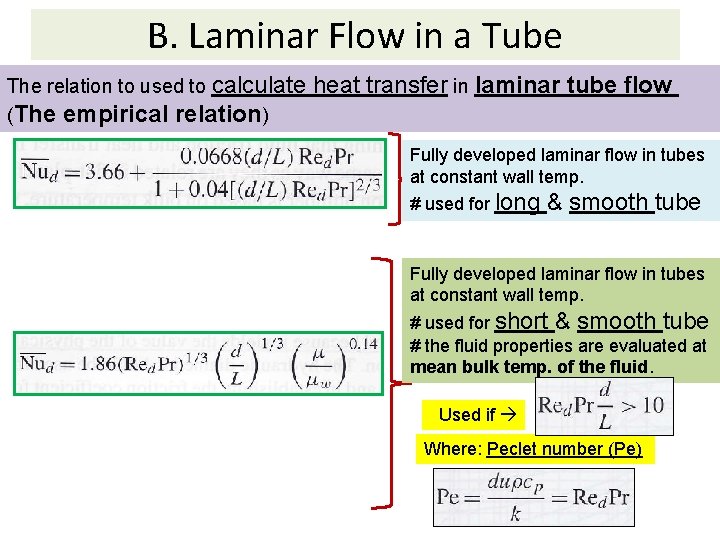
B. Laminar Flow in a Tube The relation to used to calculate (The empirical relation) heat transfer in laminar tube flow Fully developed laminar flow in tubes at constant wall temp. # used for long & smooth tube Fully developed laminar flow in tubes at constant wall temp. # used for short & smooth tube # the fluid properties are evaluated at mean bulk temp. of the fluid. Used if Where: Peclet number (Pe)

For rough tubes (relation fluid friction and heat transfer), expressed in term of the Stanton Number: Where;

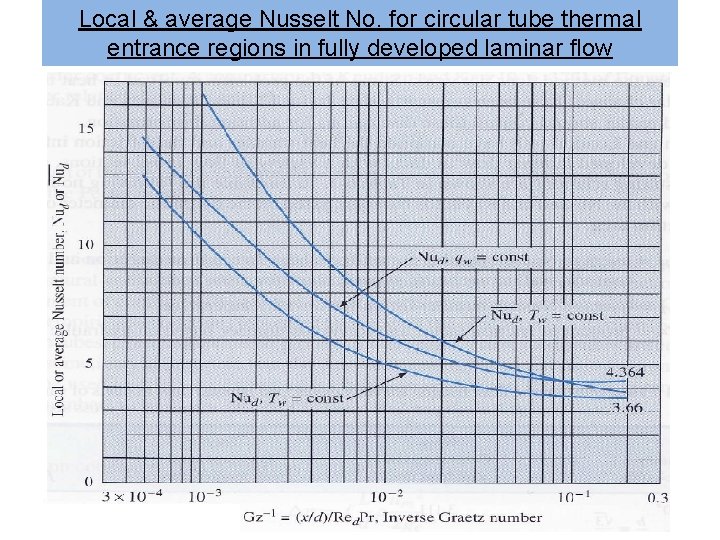
Entrance region in laminar flow : To calculate local and average Nusselt No for laminar entrance regions for the case of a fully developed velocity profile, use the Graph with “inverse Graetz number”

Local & average Nusselt No. for circular tube thermal entrance regions in fully developed laminar flow

Example 3: Heating of Water in Laminar Tube Flow Water at 60 °C enters a tube of 1 -in (2. 54 cm) diameter at a mean flow velocity of 2 cm/s. Calculate the exit water temp. if the tube is 3. 0 m long and the wall temp. is constant at 80 °C.

Example 3 -Solution a. Evaluate air properties at inlet bulk temperature; 60◦C+273 K = 333 K b. From the Table given; interpolate data… c. Determine flow regime; calculate for Re LAMINAR! d. Calculate Peclet n. (Pe) e. Therefore, use f. Evaluate µw at wall temp. 80◦C (176 F) from Table A-9, g. Calculate for h, h. Determine the outlet bulk temperature (Tb 2); from the energy balance equation:

Example 3 -Solution (continue) i. Calculate the mass flow rate j. Substitute all values into the energy balance equation for Tb 2 d. Calculate the mean bulk temp. e. Evaluate properties at mean bulk temp. (interpolate data from the Table) g. Determine Re. no. & Peclet no. h. Calculate for h, h. Insert h into the energy balance equation:

Example 4: Heating of Air in Laminar Tube Flow for Constant Heat Flux Air at 1 atm and 27 °C enters a 5. 0 mm diameter smooth tube with a velocity of 3. 0 m/s. The length of the tube is 10 cm. A constant heat flux is imposed on the tube wall. a) Calculate the heat transfer if the exit bulk temp. is 77 °C. b) Calculate the exit wall temp. and the value of h at exit.

Example 4 -Solution a. Evaluate air properties at average bulk temperature; b. From the Table given; interpolate data… c. Determine flow regime; calculate for Re LAMINAR! d. Since the tube is rather short (10 cm), expect a thermal entrance effect ; thus calculate inverse Gz no. : e. Since qw=constant; obtain Nusselt no. at exit from the graph g. Total heat transfer from the overall energy balance f. At entrance, h. Therefore, q if exit bulk temp is 77◦C ṁ = pumᴨd 2/4

Example 4 -Solution i. Calculate exit wall temp. , determine qw: From j. Calculate h at exit;

Example 5: Heating of Air with Isothermal Tube Wall Air at 1 atm and 27 °C enters a 5. 0 mm diameter smooth tube with a velocity of 3. 0 m/s. The length of the tube is 10 cm. A constant wall temp. is imposed on the tube wall. a) Calculate the heat transfer if the exit bulk temp. is 77 °C b) Calculate the exit wall temp. and the value of h at exit

Example 5 -Solution a. Evaluate air properties at average bulk temperature; b. From the Table given; interpolate data… c. Determine flow regime; calculate for Re LAMINAR! d. Since the tube is rather short (10 cm), expect a thermal entrance effect ; thus calculate inverse Gz no. : e. Since Tw=constant; obtain Nusselt no. at exit from the graph g. Calculate average heat-transfer coefficient: f. Calculate heat transfer based on a mean bulk temperature of 52◦C and h value Nud = 5. 15

FREE CONVECTION Fluid flow is induced by density differences caused by temperature differences The vertical plate is heated and the free convection boundary layer is formed. The velocity profile differs from that in a forced convection system in that the velocity at the wall is zero and also zero at the other edge of the boundary layer since the free stream velocity is zero for natural convection. The boundary layer initially is laminar as shown but at some distances from the leading edge it starts to become turbulent. The wall temperature is Tw and the bulk temperature is Tb.

1. General correlation for Free Convection In many different geometries, the average Nusselt number may be calculated by as: Ra=

A. FREE CONVECTION FOR VERTICAL PLATES AND CYLINDER • Isothermal vertical plates: L = height of plate. • Vertical cylinders: treat as vertical plates, if D/L ≥ 35/Gr 1/4 = For Ra. L < 109 = 0. 85 + For 10 -1 < Ra. L < 1012

A. FREE CONVECTION FOR VERTICAL PLATES AND CYLINDER Constant Heat Flux Surfaces For laminar For tubulent = = 0. 60 = 0. 17 105 < Grx*Pr < 1011 ; qw constant 2 x 1013 < Grx*Pr < 1016 ; qw constant

B. FREE CONVECTION FOR HORIZONTAL CYLINDER • Constants C and m from table • Tube diameter is characteristic length For 10 -5 < Gr Pr < 1012 For laminar 10 -6 < Gr Pr < 109 Heat transfer from horizontal cylinder to liquid metals

C. FREE CONVECTION FOR HORIZONTAL PLATES • Characteristic length: L = A/P • where A is the area and P the perimeter of the surface. For Gr. L Pr < 2 X 108 Heated surface facing upward For 2 X 108 <Gr. L Pr < 1011 For 106 <Gr. L Pr <1011 Heat flux Heated surface facing downward

THANK YOU