PTICA LA LUZ ES UNA ONDA ELECTROMAGNTICA LA

ÓPTICA LA LUZ ES UNA ONDA ELECTROMAGNÉTICA LA LUZ ES LA PARTE DEL ESPECTRO E. M. QUE PODEMOS VER CON NUESTROS OJOS

ESPECTRO VISIBLE 400 nm < < 650 nm

Maxwell propuso que un campo eléctrico variable en el tiempo produce un campo magnético al igual que las corrientes

Ec. de Maxwell en el vacío 0 Gauss para E Gauss para B Faraday Ampere. Maxwell

Predice ondas electromagnéticas que se propagan con una velocidad v = 1/ 0 0 Este valor coincide con la velocidad de la luz 8 c = 3 x 10 m/s

Ondas em Ex = E 0 sen[k(z - vt) ] By = B 0 sen[k(z - vt) ] E S B B 0 = E 0 /c

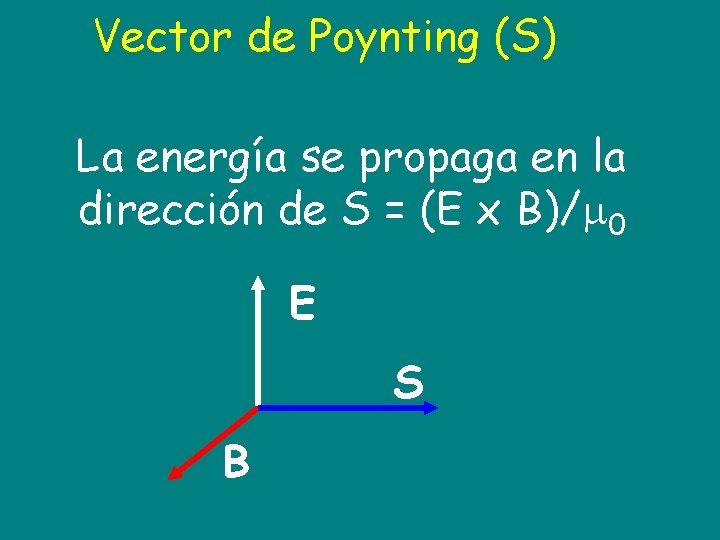
Vector de Poynting (S) La energía se propaga en la dirección de S = (E x B)/ 0 E S B

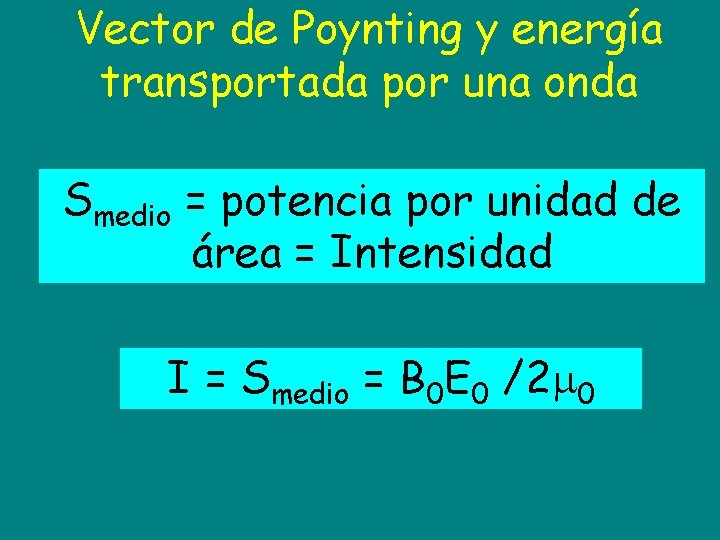
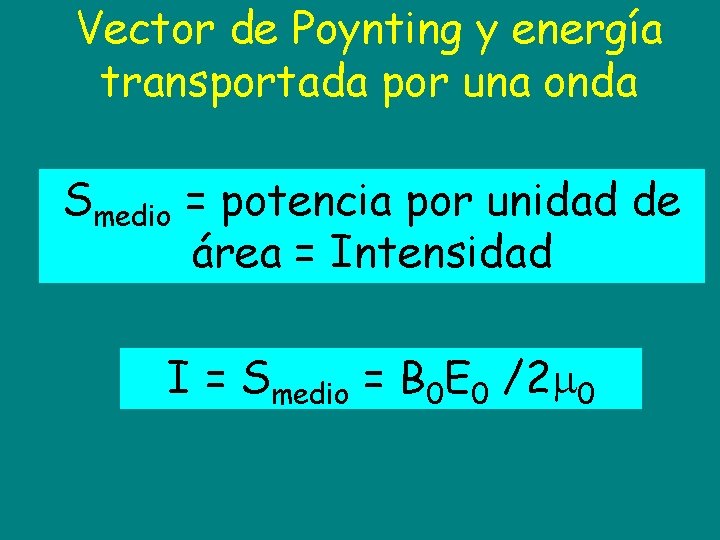
Vector de Poynting y energía transportada por una onda Smedio = potencia por unidad de área = Intensidad I = Smedio = B 0 E 0 /2 0

Vector de Poynting y energía transportada por una onda Smedio = potencia por unidad de área = Intensidad I = Smedio = B 0 E 0 /2 0

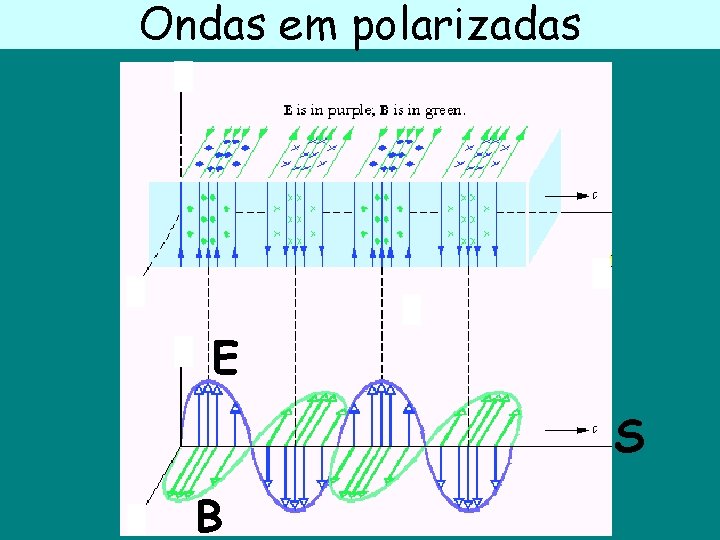
Ondas em polarizadas Ex = E 0 sen[k(z - vt) ] By = B 0 sen[k(z - vt) ] x E S z y B B 0 = E 0 /c

Ondas em polarizadas E S B

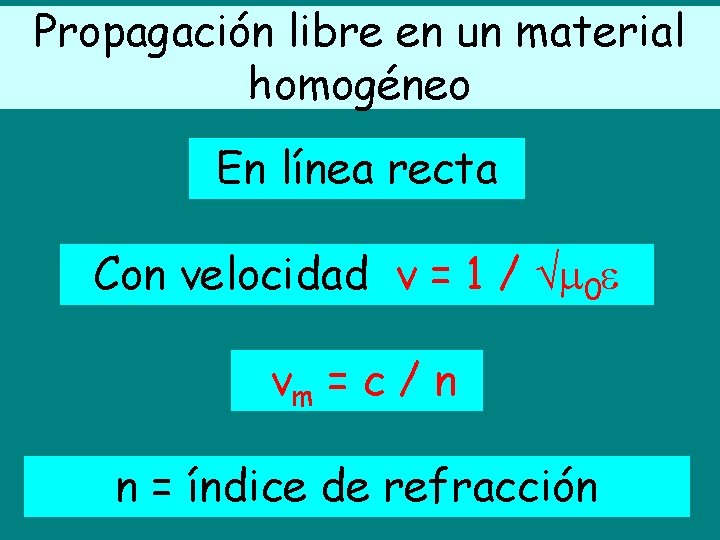
Propagación libre en un material homogéneo En línea recta Con velocidad v = 1 / 0 vm = c / n n = índice de refracción

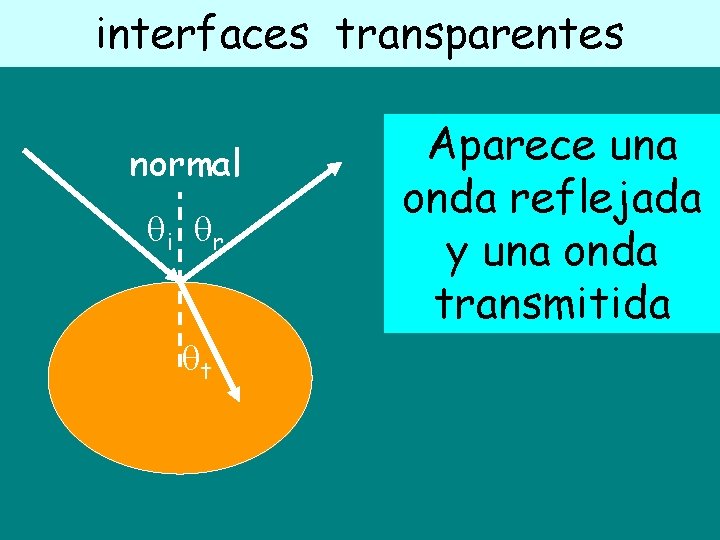
interfaces transparentes normal i r t Aparece una onda reflejada y una onda transmitida

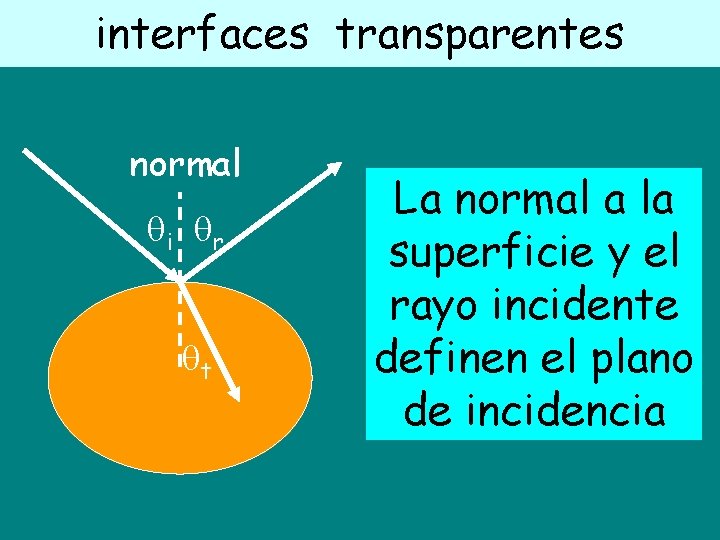
interfaces transparentes normal i r t La normal a la superficie y el rayo incidente definen el plano de incidencia

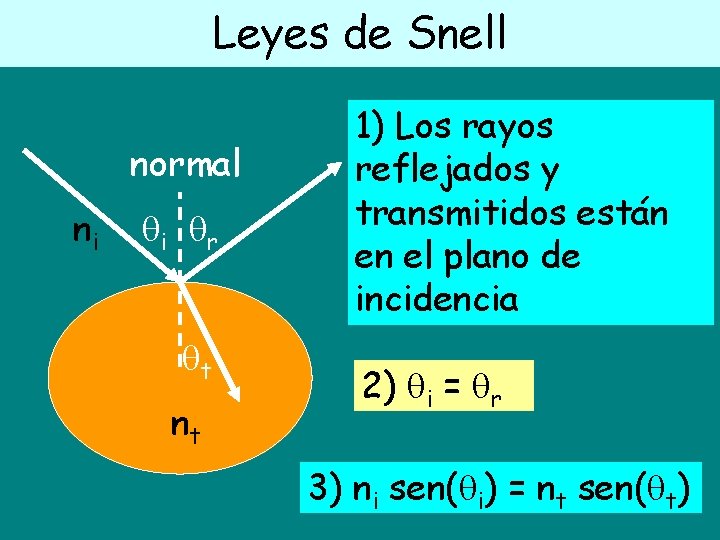
Leyes de Snell normal ni i r t nt 1) Los rayos reflejados y transmitidos están en el plano de incidencia 2) i = r 3) ni sen( i) = nt sen( t)

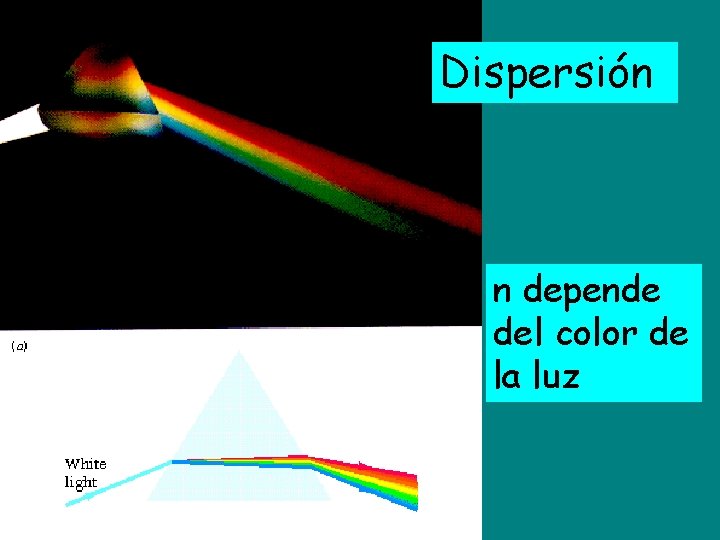
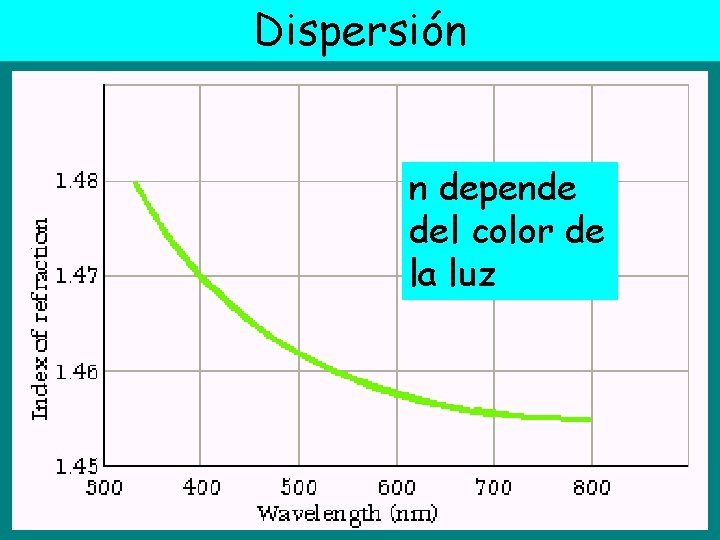
Dispersión n depende del color de la luz

Dispersión n depende del color de la luz

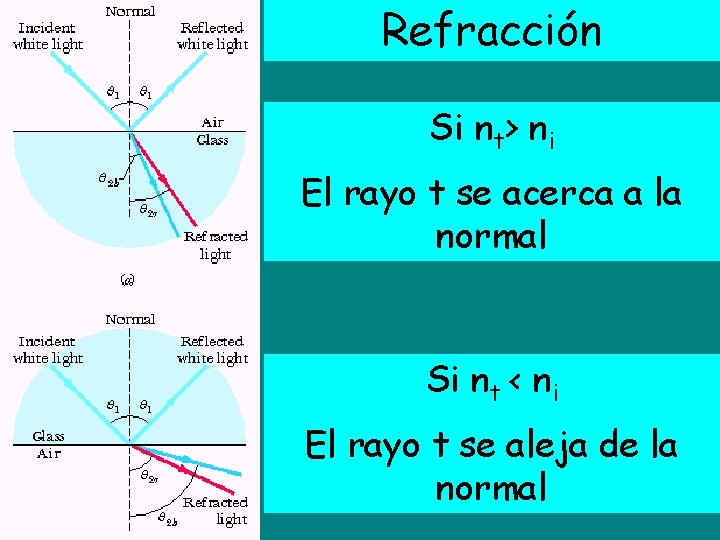
Refracción Si nt> ni El rayo t se acerca a la normal Si nt < ni El rayo t se aleja de la normal

Intensidad reflejada Ii Ir ni Para incidencia normal Ir = [(ni-nt)2/(ni+nt)2] Ii It nt It = Ii - Ir Ir/Ii = 5 % para vidrio

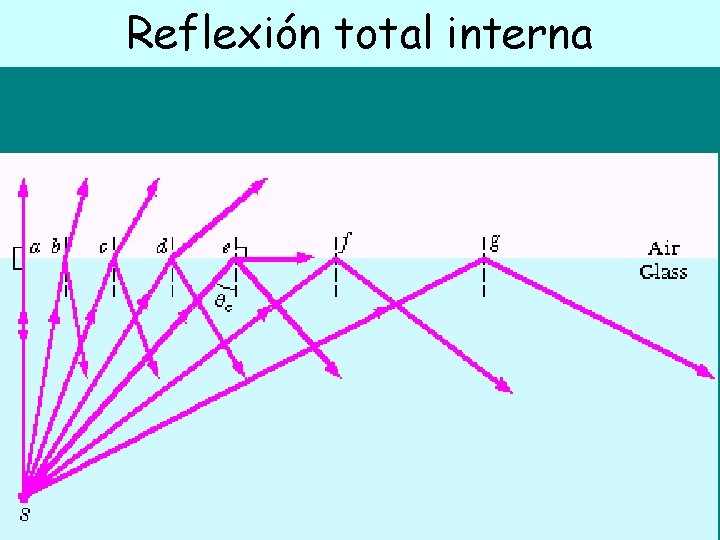
Reflexión total interna

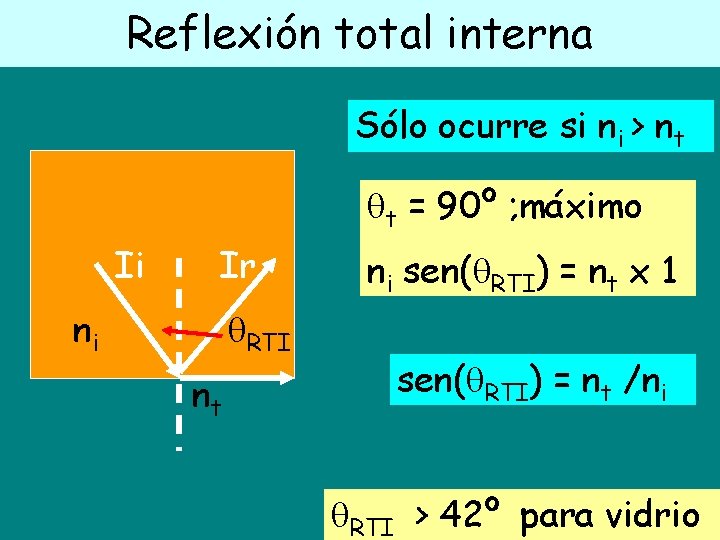
Reflexión total interna Sólo ocurre si ni > nt t = 90º ; máximo Ii Ir ni RTI nt ni sen( RTI) = nt x 1 sen( RTI) = nt /ni RTI > 42º para vidrio

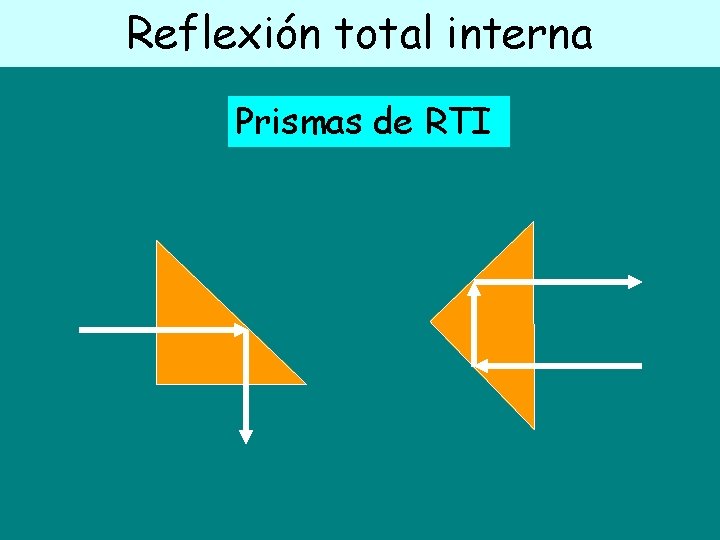
Reflexión total interna Prismas de RTI

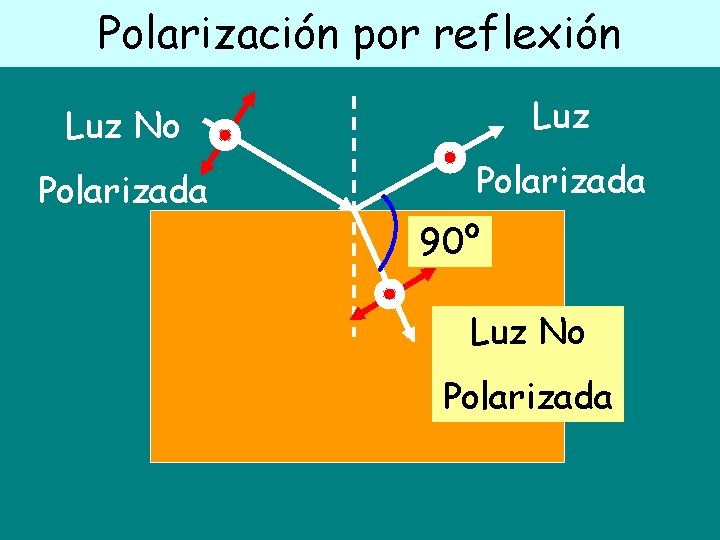
Polarización por reflexión Luz No Luz Polarizada 90º Luz No Polarizada

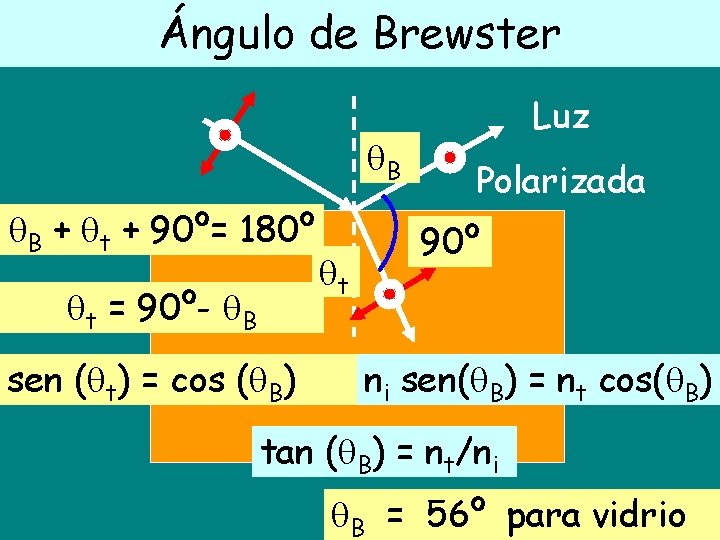
Ángulo de Brewster B B + t + 90º= 180º t = 90º- B sen ( t) = cos ( B) t Luz Polarizada 90º ni sen( B) = nt cos( B) tan ( B) = nt/ni B = 56º para vidrio

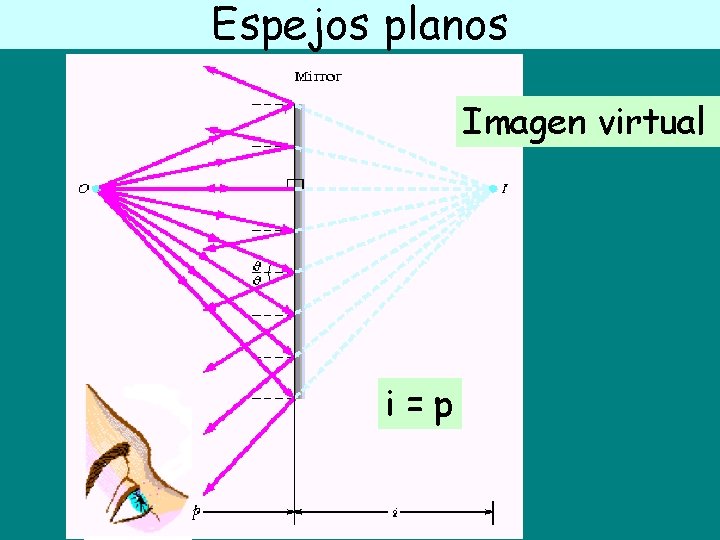
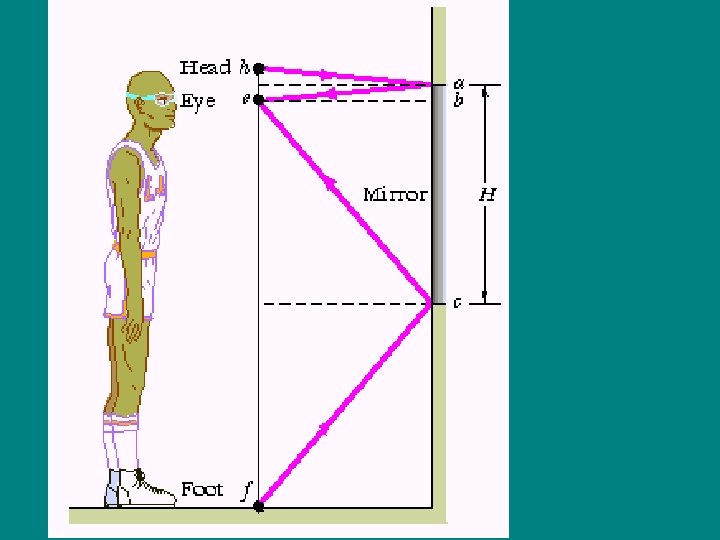
Espejos planos Imagen virtual i=p