PTICA GEOMTRICA Prof Luiz Odizo CONCEITOS GERAIS 01

ÓPTICA GEOMÉTRICA Prof. Luiz Odizo

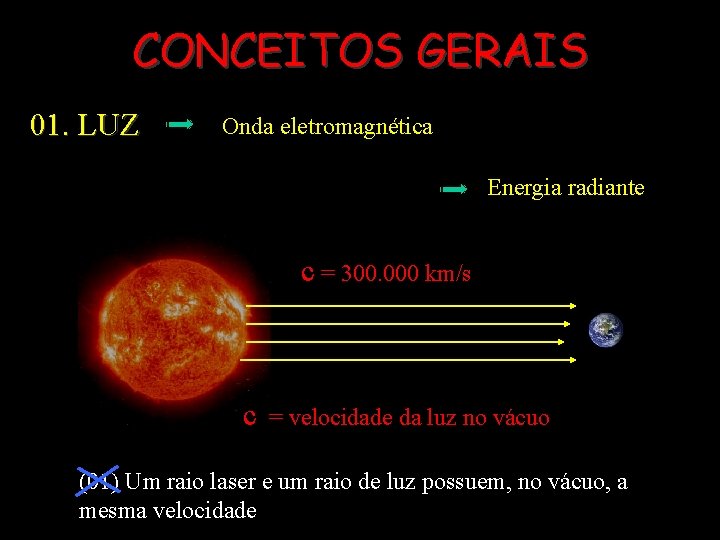
CONCEITOS GERAIS 01. LUZ Onda eletromagnética Energia radiante c = 300. 000 km/s c = velocidade da luz no vácuo (01) Um raio laser e um raio de luz possuem, no vácuo, a mesma velocidade

OBSERVAÇÕES Todas as ondas eletromagnéticas, possuem, no vácuo, a mesma velocidade (300. 000 km/s) ANO – LUZ “ É a distância percorrida pela Luz, no vácuo, em 1 ano ” 1 ano-luz 9, 5 x 1012 km S = v x t S = 3 x 105 x 1 ano( 3, 16 x 107 s) S 9, 5 x 1012 km

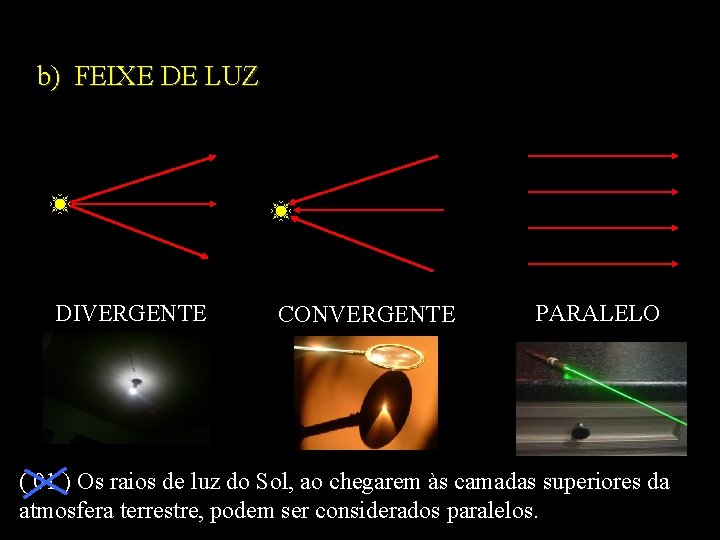
b) FEIXE DE LUZ DIVERGENTE CONVERGENTE PARALELO ( 01 ) Os raios de luz do Sol, ao chegarem às camadas superiores da atmosfera terrestre, podem ser considerados paralelos.

c) FONTES DE LUZ PRIMÁRIA (CORPOS LUMINOSOS): Aqueles que emitem luz própria Ex: Lâmpada, Estrelas etc SECUNDÁRIA (CORPOS ILUMINADOS): Aqueles que emitem apenas a luz recebida de outros corpos Ex: Lua, quadro etc NOTA: Fontes Pontuais são aquelas que possuem dimensões Pontuais desprezíveis em relação a um determinado referencial

d) MEIOS DE PROPAGAÇÃO DA LUZ TRANSPARENTES: são aqueles que permitem a propagação regular da luz, proporcionando uma visão nítida dos objetos. (Ex: ar, vidro, água em pequenas camadas) TRANSLÚCIDOS: são aqueles no qual a luz se propaga de maneira irregular, não permitindo uma visão nítida dos objetos. (Ex: papel vegetal, vidro fosco) OPACOS: são aqueles que não permitem a passagem da luz TRANSLÚCIDO TRANSPARENTE OPACO

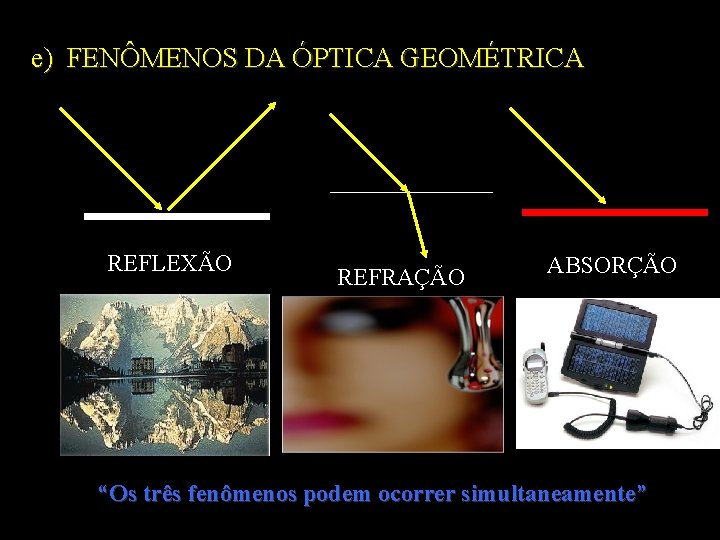
e) FENÔMENOS DA ÓPTICA GEOMÉTRICA REFLEXÃO REFRAÇÃO ABSORÇÃO “Os três fenômenos podem ocorrer simultaneamente”

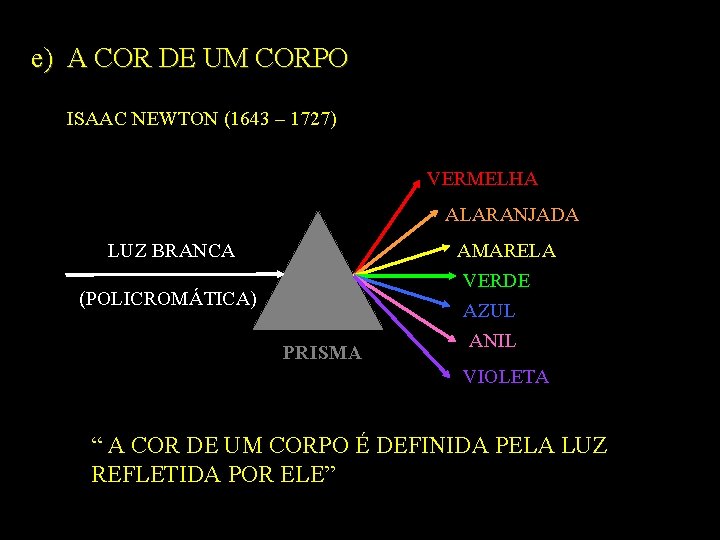
e) A COR DE UM CORPO ISAAC NEWTON (1643 – 1727) VERMELHA ALARANJADA LUZ BRANCA AMARELA (POLICROMÁTICA) PRISMA VERDE AZUL ANIL VIOLETA “ A COR DE UM CORPO É DEFINIDA PELA LUZ REFLETIDA POR ELE”

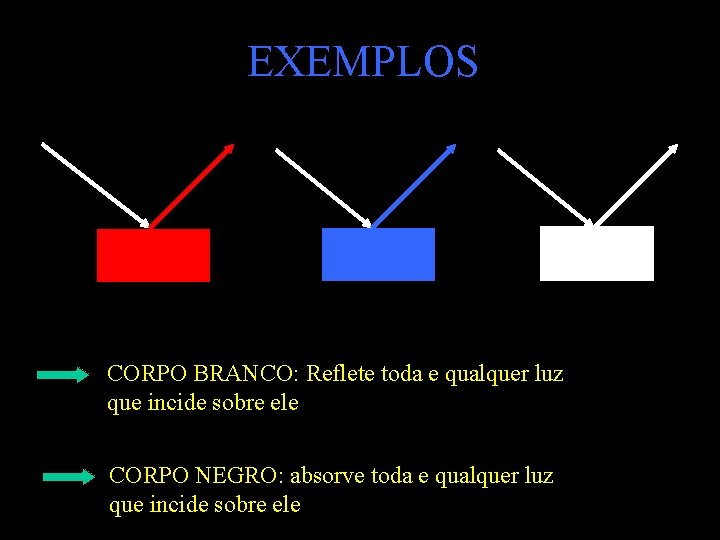
EXEMPLOS CORPO BRANCO: Reflete toda e qualquer luz que incide sobre ele CORPO NEGRO: absorve toda e qualquer luz que incide sobre ele

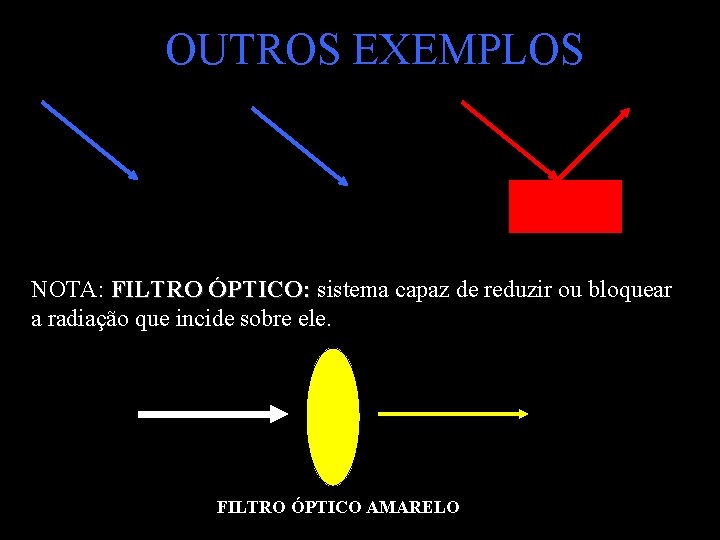
OUTROS EXEMPLOS NOTA: FILTRO ÓPTICO: sistema capaz de reduzir ou bloquear ÓPTICO: a radiação que incide sobre ele. FILTRO ÓPTICO AMARELO

f) PRINCÍPIOS DA ÓPTICA GEOMÉTRICA REVERSIBILIDADE DOS RAIOS LUMINOSOS “A trajetória da luz não depende do seu sentido de percurso”

INDEPENDÊNCIA DOS RAIOS LUMINOSOS “Cada raio de luz se propaga independentemente de qualquer outro raio”

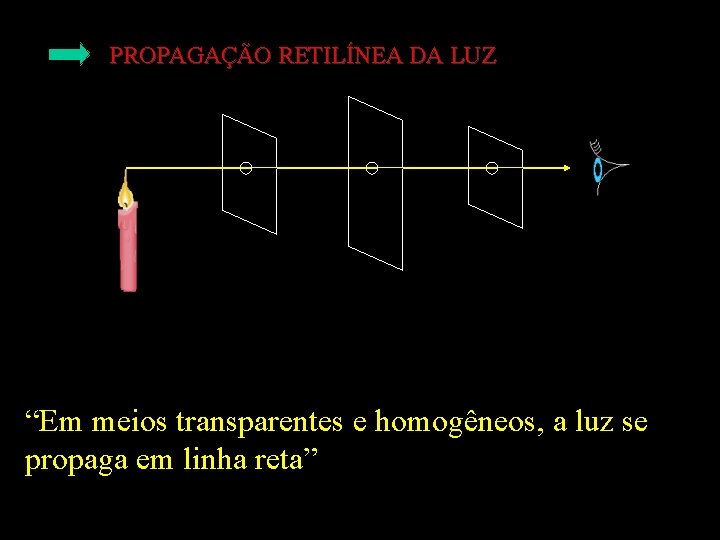
PROPAGAÇÃO RETILÍNEA DA LUZ “Em meios transparentes e homogêneos, a luz se propaga em linha reta”

EVIDÊNCIAS DA PROPAGAÇÃO RETILÍNEA DA LUZ a) SOMBRA região não iluminada, delimitada pelos raios que tangenciam o objeto não u SOMBRA FONTE DE LUZ PONTUAL OBJETO ANTEPARO

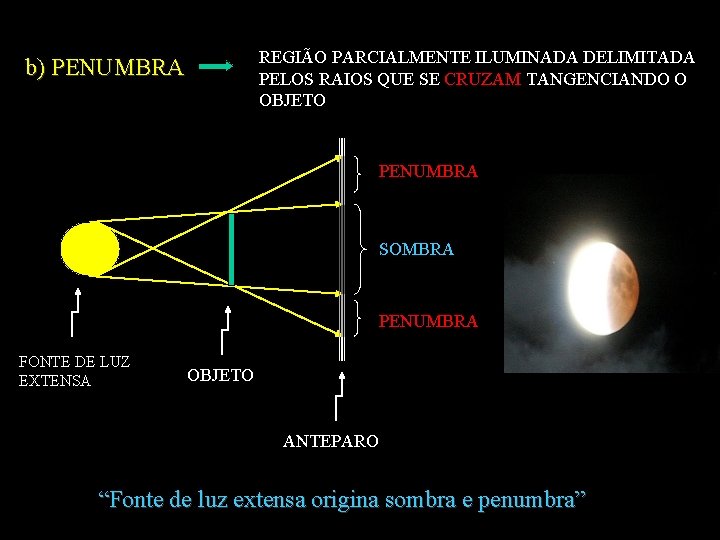
REGIÃO PARCIALMENTE ILUMINADA DELIMITADA PELOS RAIOS QUE SE CRUZAM TANGENCIANDO O OBJETO b) PENUMBRA SOMBRA PENUMBRA FONTE DE LUZ EXTENSA OBJETO ANTEPARO “Fonte de luz extensa origina sombra e penumbra”

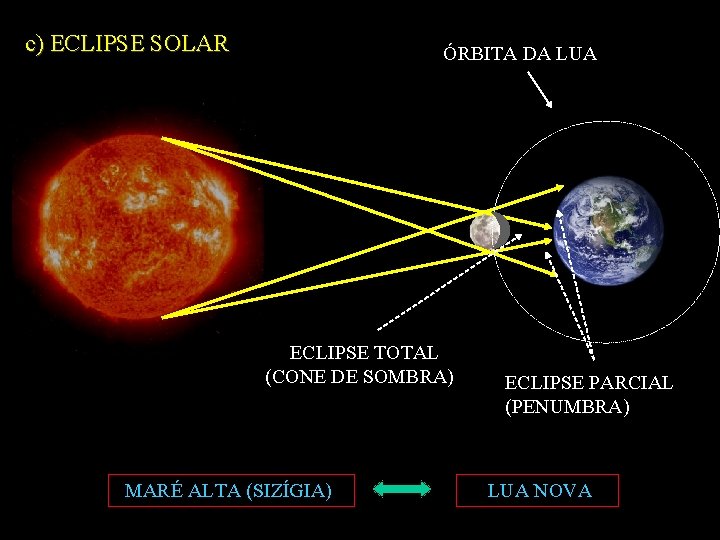
c) ECLIPSE SOLAR ÓRBITA DA LUA ECLIPSE TOTAL (CONE DE SOMBRA) MARÉ ALTA (SIZÍGIA) ECLIPSE PARCIAL (PENUMBRA) LUA NOVA

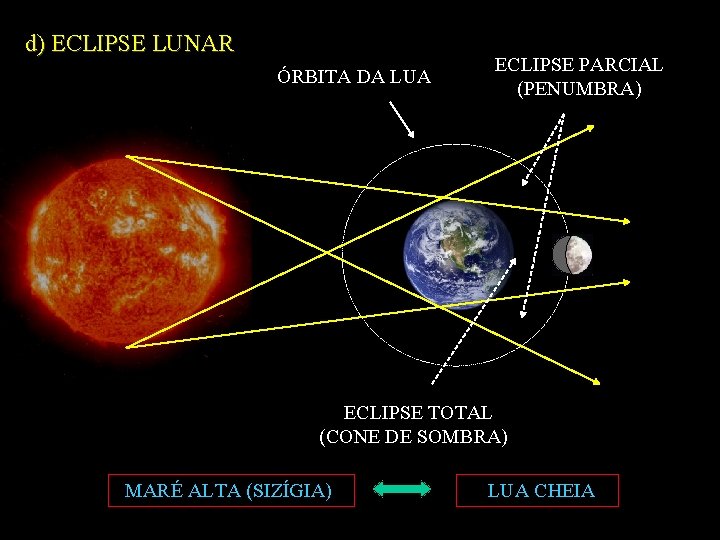
d) ECLIPSE LUNAR ÓRBITA DA LUA ECLIPSE PARCIAL (PENUMBRA) ECLIPSE TOTAL (CONE DE SOMBRA) MARÉ ALTA (SIZÍGIA) LUA CHEIA

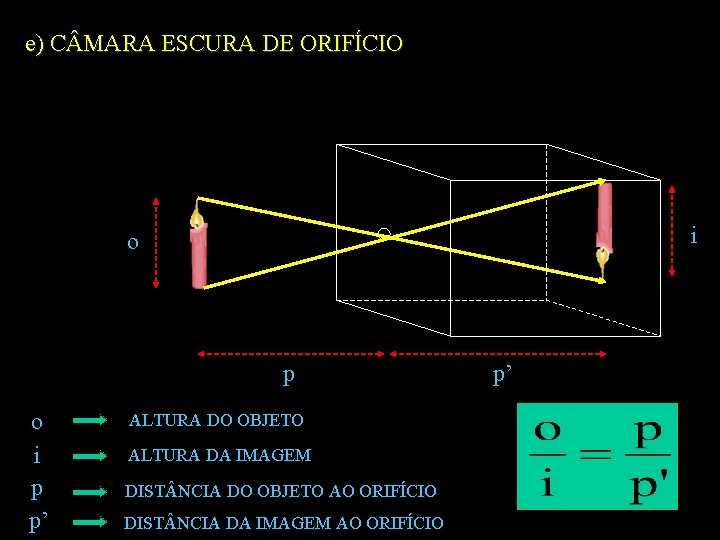
e) C MARA ESCURA DE ORIFÍCIO i o p o i p p’ ALTURA DO OBJETO ALTURA DA IMAGEM DIST NCIA DO OBJETO AO ORIFÍCIO DIST NCIA DA IMAGEM AO ORIFÍCIO p’

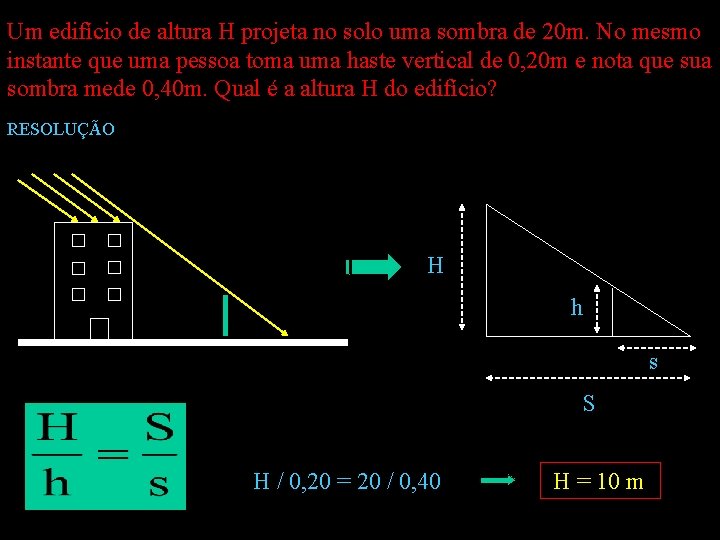
Um edifício de altura H projeta no solo uma sombra de 20 m. No mesmo instante que uma pessoa toma uma haste vertical de 0, 20 m e nota que sua sombra mede 0, 40 m. Qual é a altura H do edifício? RESOLUÇÃO H h s S H / 0, 20 = 20 / 0, 40 H = 10 m

EXERCÍCIOS 01. A velocidade de propagação das ondas luminosas: a) é infinitamente grande b) é máxima no ar c) é maior na água do que no vácuo d) vale 300. 000 km/s no vidro e) vale 3, 00 x 1010 cm/s no vácuo 02. (Fuvest-SP) Uma estrela emite radiação que percorre a distância de 1 bilhão de anos-luz até chegar à Terra e ser captada por um telescópio. Isso quer dizer que: a) A estrela está a 1 bilhão de quilômetros da Terra b) Daqui a 1 bilhão de anos, a radiação da estrela não será mais observada na Terra c) A radiação recebida hoje na Terra foi emitida pela estrela há 1 bilhão de anos d) Quando a radiação foi emitida pela estrela, ela tinha idade de 1 bilhão de anos

03. (UEFS/03 -2) Um objeto vermelho, tingido com pigmentos puros, quando colocado em uma sala iluminada com luz monocromática amarela, será visto na cor a) amarela b) azul c) vermelha d) preta e) violeta 04. (FDC/03) Ao incidir luz em um objeto opaco, de superfície branca e não polida, observa-se predominantemente, a ocorrência de a) reflexão especular b) reflexão difusa c) refração d) difração e) absorção

05. (UCSAL/03) Você vê uma árvore através do vidro de uma janela. A luz refletida por essa árvore propaga-se pelo ar, atravessa o vidro e volta a se propagar no ar até atingir seus olhos. Supondo-se todos os meios homogêneos, desde que a luz é refletida pela árvore até atingir seus olhos a) ocorre uma refração b) ocorrem duas refrações c) ocorrem três refrações d) ocorrem quatro refrações e) ocorrem cinco refrações 06. Um estudante que contemple um arco-íris através de um filtro óptico amarelo: a) verá o arco-íris, com todas as suas cores b) não verá nada do arco-íris c) verá apenas a faixa amarela do arco-íris d) verá todas as faixas do arco-íris, exceto a amarela e) verá apenas as faixas alaranjada, amarela e verde do arco-íris

07. Um grupo de escoteiros deseja construir um acampamento em torno de uma árvore. Por segurança, eles devem colocar as barracas a uma distância tal da base da árvore que, se ela cair, não venha a atingi-los. Aproveitando o dia ensolarado, eles mediram, ao mesmo tempo, os comprimentos das sombras da árvore e de um deles, que tem 1, 5 m de altura; os valores encontrados foram 6, 0 m e 1, 8 m, respectivamente. Qual deve ser a menor distância das barracas à base da árvore? R = 5 m 08. Um disco opaco de 20 cm de raio dista 0, 50 m de uma fonte puntiforme luminosa. Uma tela é colocada a 1, 50 m atrás do disco, de forma que a reta que passa pela fonte e pelo centro do disco é perpendicular à tela e esta é paralela ao disco. O diâmetro da sombra do disco projetada na tela, em centímetros, vale: R = 160 cm

09. (UESB/05) Em uma câmara escura de orifício, construída artesanalmente para tirar fotografias, a distância entre o orifício e a parede interna na qual se prende o filme fotográfico é igual a 5 cm. Sabendo-se que o filme tem altura de 20 cm, pode-se afirmar que a distância mínima, em centímetros, em relação à câmara, em que uma pessoa de 1, 8 m de altura deve se posicionar, para que se obtenha uma fotografia de corpo inteiro, é igual a a) 360 b) 180 c) 90 d) 45 e) 30 10. Num eclipse total da Lua, a posição relativa dos três astros, Sol, Lua e Terra, é a seguinte: a) O Sol entre a Lua e a Terra b) A Lua entre o Sol e a Terra c) A Terra entre o Sol e a Lua d) A Terra e a Lua à esquerda do Sol e) É impossível a ocorrência de um eclipse total da Lua

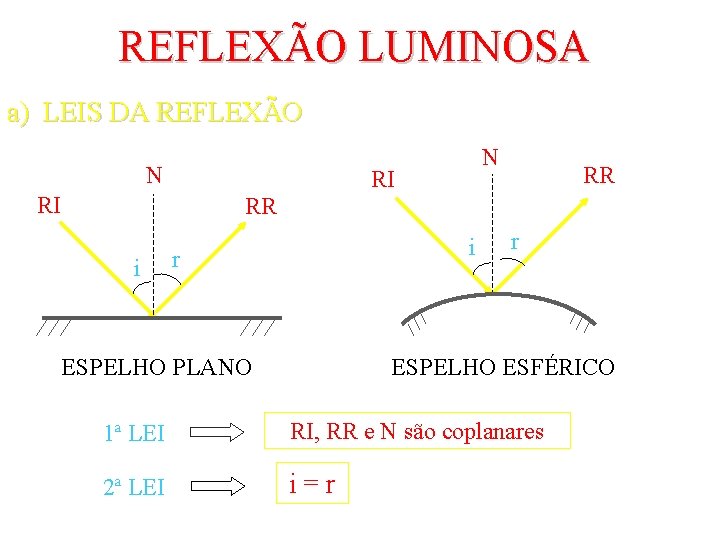
REFLEXÃO LUMINOSA a) LEIS DA REFLEXÃO N N RI RI RR RR i i r ESPELHO PLANO r ESPELHO ESFÉRICO 1ª LEI RI, RR e N são coplanares 2ª LEI i = r

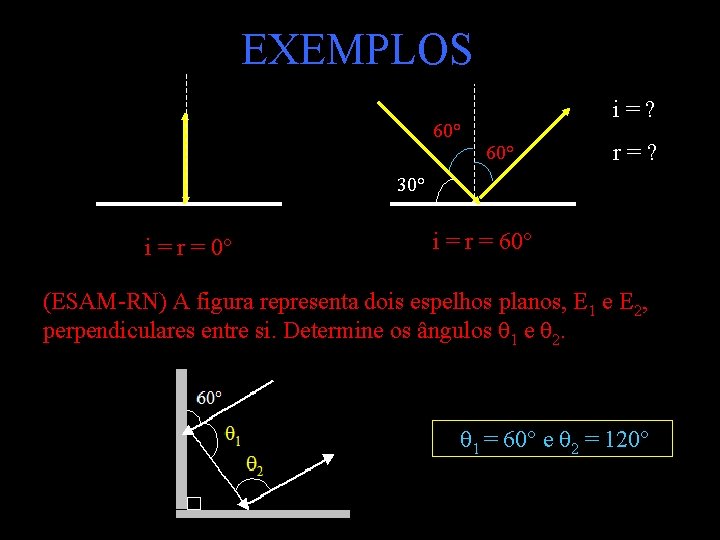
EXEMPLOS 60° i = ? 60° r = ? 30° i = r = 60° (ESAM-RN) A figura representa dois espelhos planos, E 1 e E 2, perpendiculares entre si. Determine os ângulos θ 1 e θ 2. θ 1 = 60° e θ 2 = 120°

b) ESPELHOS PLANOS (SISTEMAS ESTIGMÁTICOS) PROPRIEDADES “A distância do objeto ao espelho é igual à distância da imagem ao espelho” (EQUIDIST NCIA) “ A imagem conjugada num espelho plano é revertida em relação ao objeto” (SIMETRIA) F I N Ó R I O OBJETO OI Ò IMAGEM I

ANÁLISE GRÁFICA PONTO OBJETO Determinado pelo cruzamento dos raios incidentes PONTO IMAGEM Determinado pelo cruzamento dos raios refletidos NATUREZA REAL Determinada pelo cruzamento dos raios efetivos NATUREZA VIRTUAL Determinada pelo cruzamento dos prolongamentos dos raios

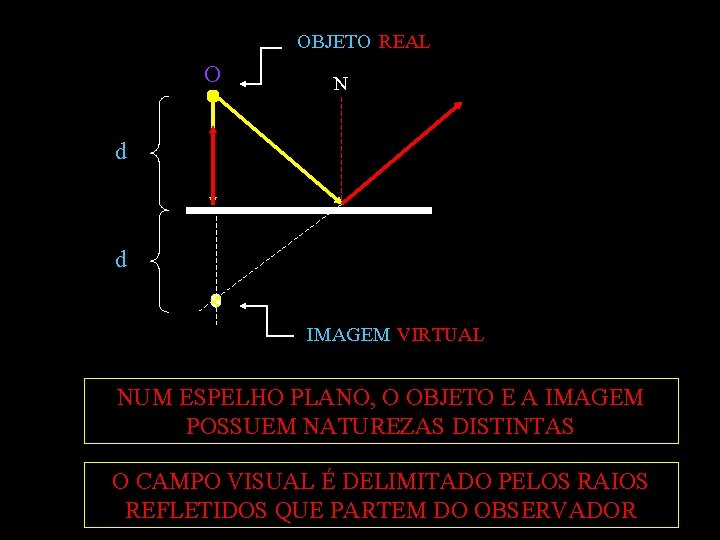
OBJETO REAL O N d d IMAGEM VIRTUAL NUM ESPELHO PLANO, O OBJETO E A IMAGEM POSSUEM NATUREZAS DISTINTAS O CAMPO VISUAL É DELIMITADO PELOS RAIOS REFLETIDOS QUE PARTEM DO OBSERVADOR

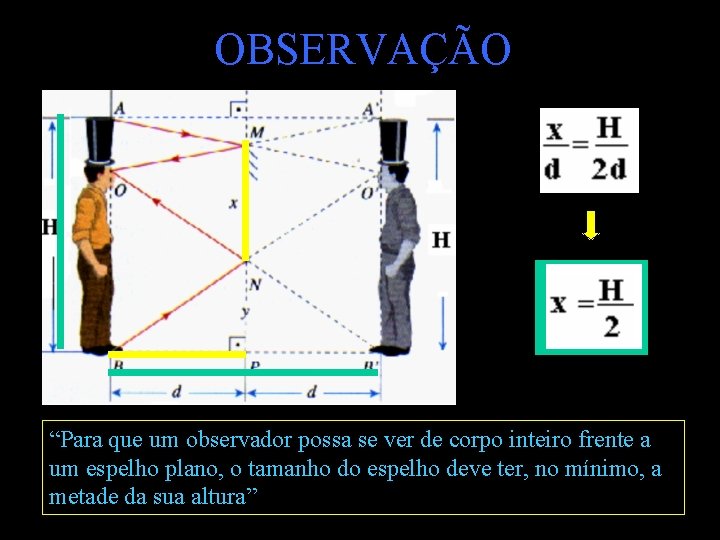
OBSERVAÇÃO “Para que um observador possa se ver de corpo inteiro frente a um espelho plano, o tamanho do espelho deve ter, no mínimo, a metade da sua altura”

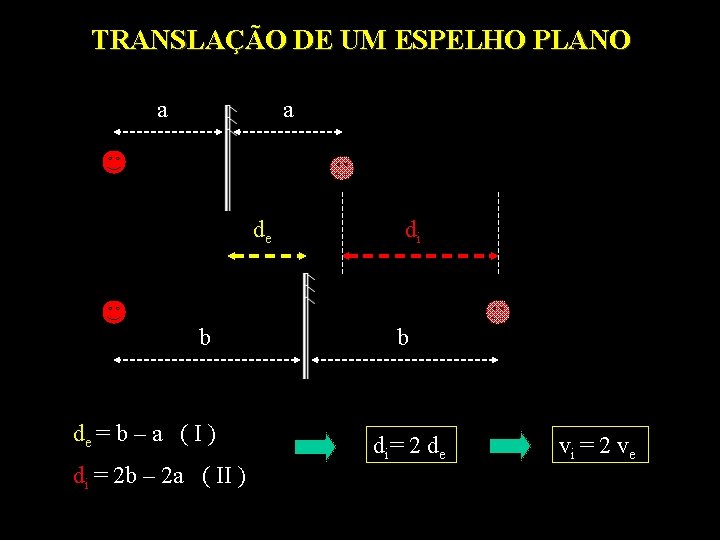
TRANSLAÇÃO DE UM ESPELHO PLANO a a de b de = b – a ( I ) di = 2 b – 2 a ( II ) di b di= 2 de vi = 2 ve

EXEMPLO (UCSAL/06) Um objeto é colocado a 20 cm de um espelho plano vertical. O espelho passa a se mover, afastando-se dele com velocidade constante de 4, 0 cm/s. Após 10 s de movimento do espelho, a distância do objeto à sua imagem fornecida pelo espelho, em cm, vale a) 40 b) 60 c) 80 d) 120 e) 200

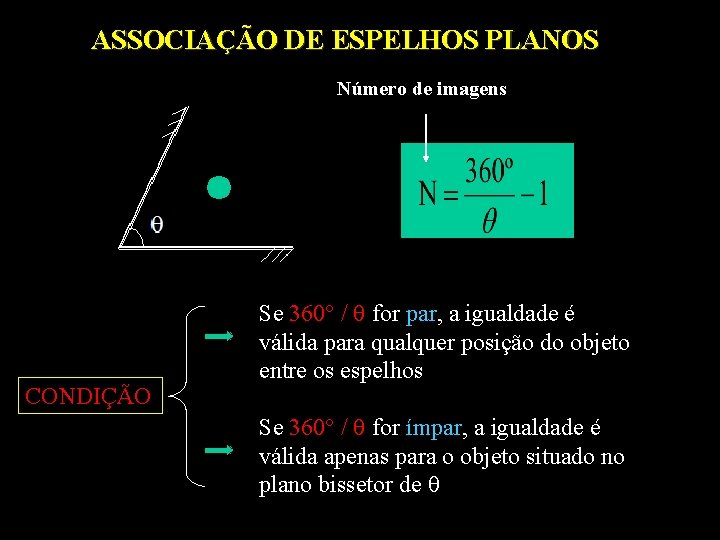
ASSOCIAÇÃO DE ESPELHOS PLANOS Número de imagens CONDIÇÃO Se 360° / for par, a igualdade é válida para qualquer posição do objeto entre os espelhos Se 360° / for ímpar, a igualdade é válida apenas para o objeto situado no plano bissetor de

EXEMPLO Com três patinadores colocados entre dois espelhos planos fixos, um diretor de cinema consegue uma cena onde são vistos, no máximo, 24 patinadores. Qual o ângulo α entre os espelhos? RESOLUÇÃO 3 patinadores 1 patinadores 21 imagens N imagens 3 x N = 24 x 1 7 = (360 / ) - 1 N = 7 = 45°

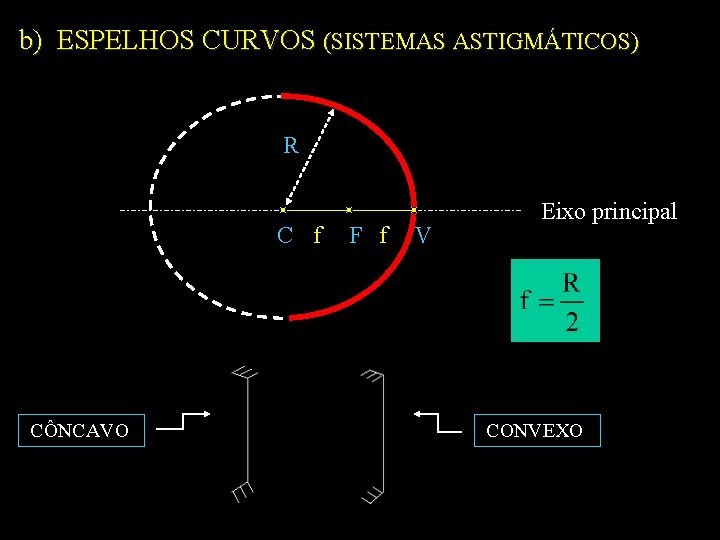
b) ESPELHOS CURVOS (SISTEMAS ASTIGMÁTICOS) R C f CÔNCAVO F f V Eixo principal CONVEXO

OBSERVAÇÕES CONDIÇÃO DE NITIDEZ DE GAUSS “Para que um espelho curvo conjugue uma imagem nítida do objeto é necessário que o seu ângulo de curvatura seja menor que 10°” FOCOS SECUNDÁRIOS São aqueles que não se situam no eixo principal, porém no mesmo plano do foco principal

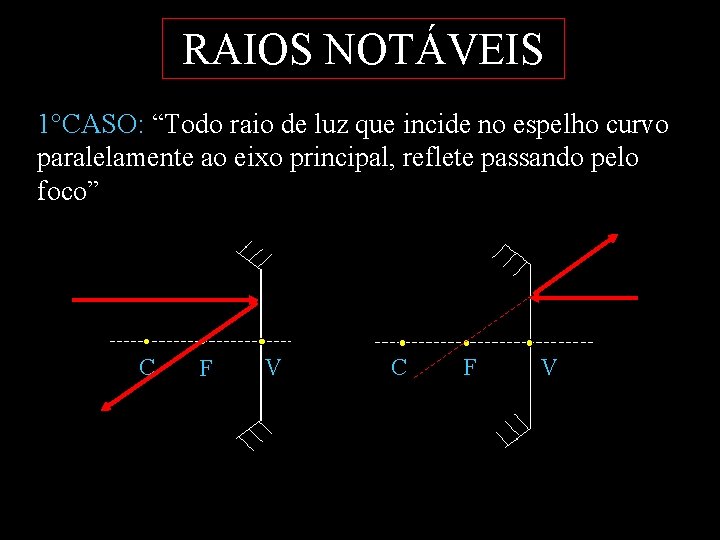
RAIOS NOTÁVEIS 1°CASO: “Todo raio de luz que incide no espelho curvo paralelamente ao eixo principal, reflete passando pelo foco” C F V

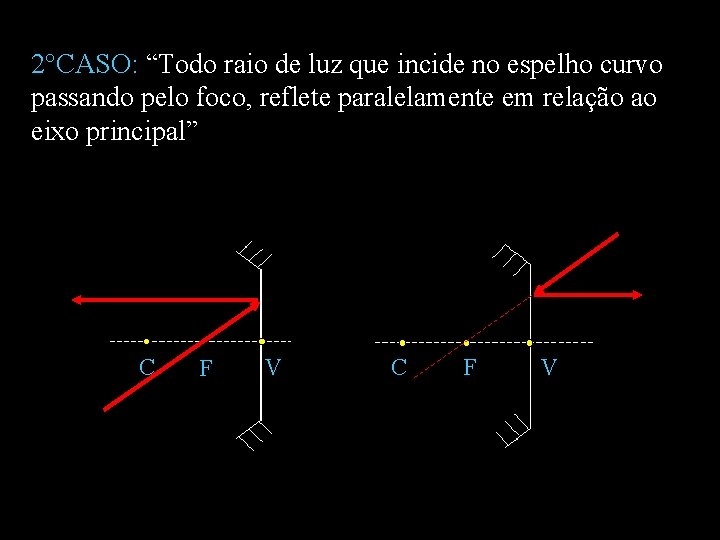
2°CASO: “Todo raio de luz que incide no espelho curvo passando pelo foco, reflete paralelamente em relação ao eixo principal” C F V

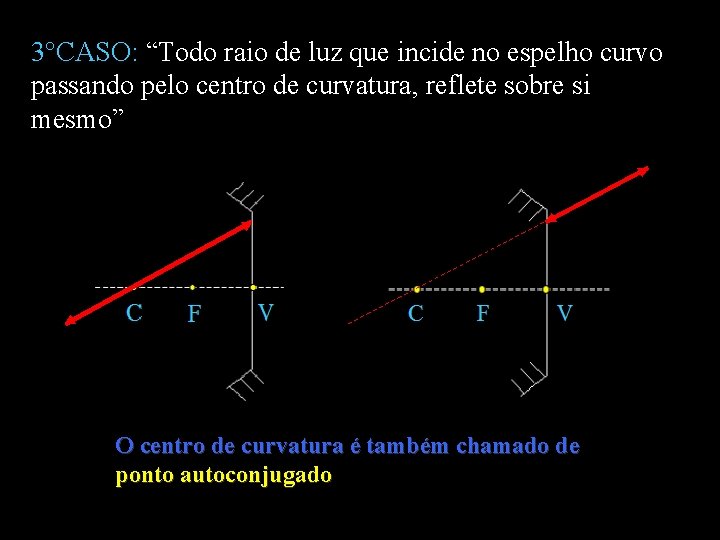
3°CASO: “Todo raio de luz que incide no espelho curvo passando pelo centro de curvatura, reflete sobre si mesmo” O centro de curvatura é também chamado de ponto autoconjugado

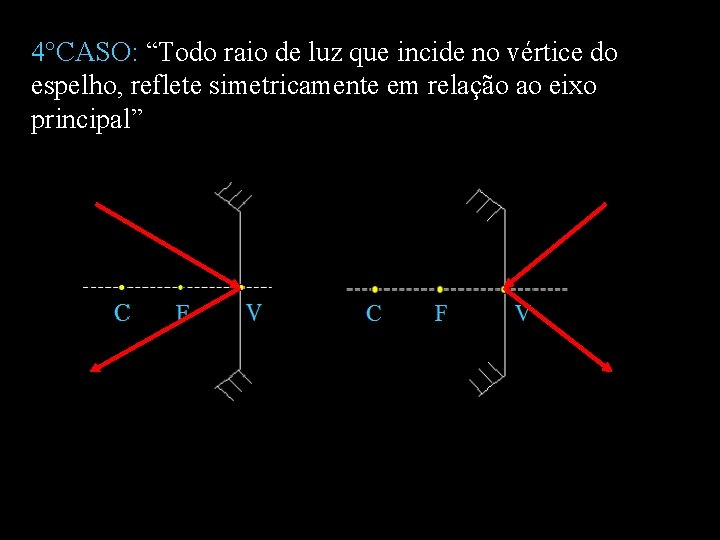
4°CASO: “Todo raio de luz que incide no vértice do espelho, reflete simetricamente em relação ao eixo principal”

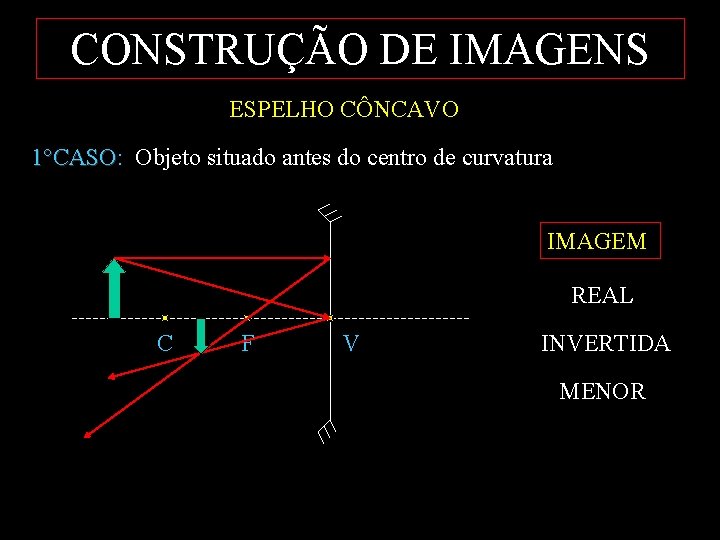
CONSTRUÇÃO DE IMAGENS ESPELHO CÔNCAVO 1°CASO: Objeto situado antes do centro de curvatura 1°CASO IMAGEM REAL C F V INVERTIDA MENOR

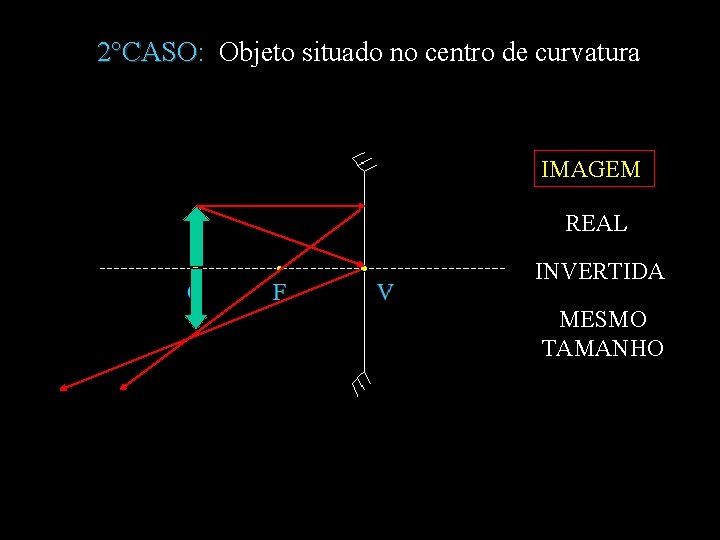
2°CASO: Objeto situado no centro de curvatura 2°CASO IMAGEM REAL INVERTIDA MESMO TAMANHO

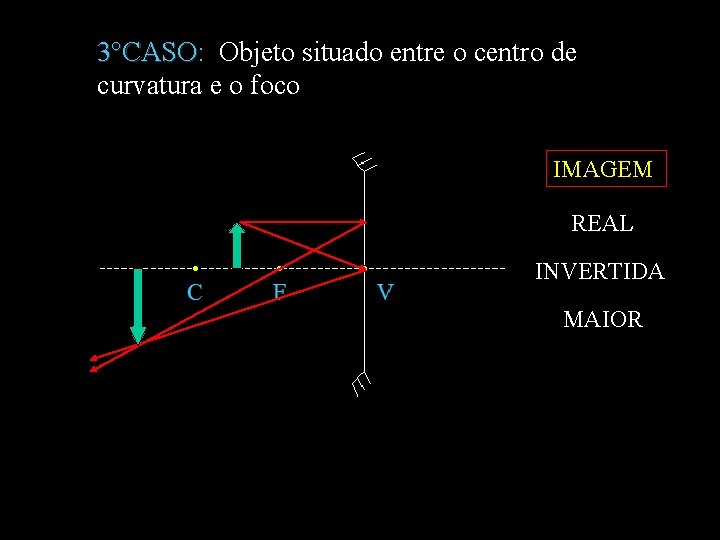
3°CASO: Objeto situado entre o centro de 3°CASO curvatura e o foco IMAGEM REAL INVERTIDA MAIOR

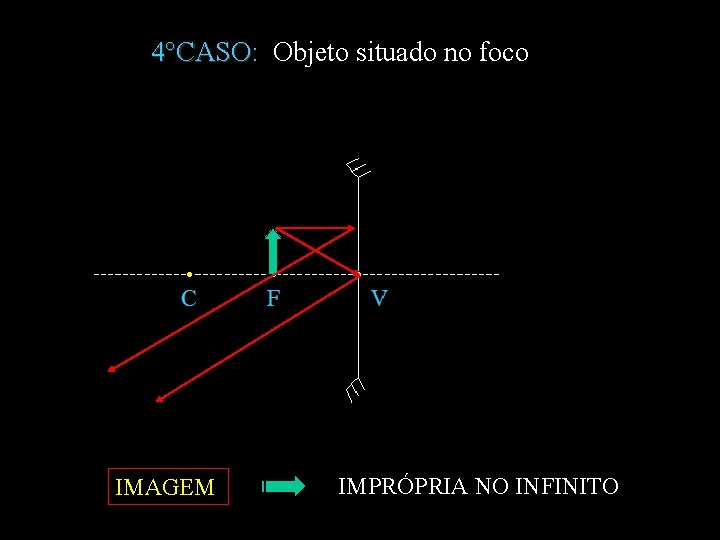
4°CASO: Objeto situado no foco 4°CASO IMAGEM IMPRÓPRIA NO INFINITO

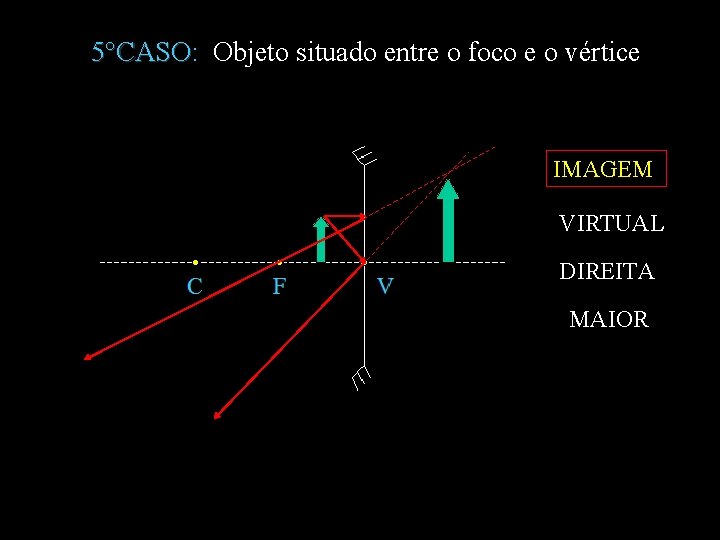
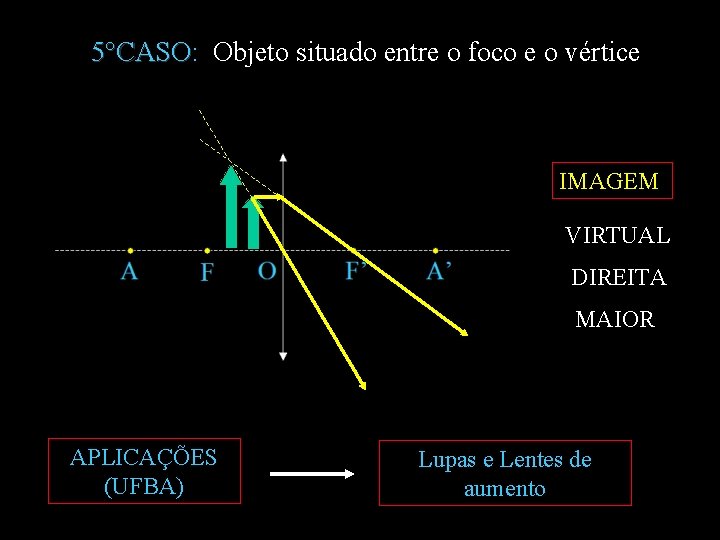
5°CASO: Objeto situado entre o foco e o vértice 5°CASO IMAGEM VIRTUAL DIREITA MAIOR

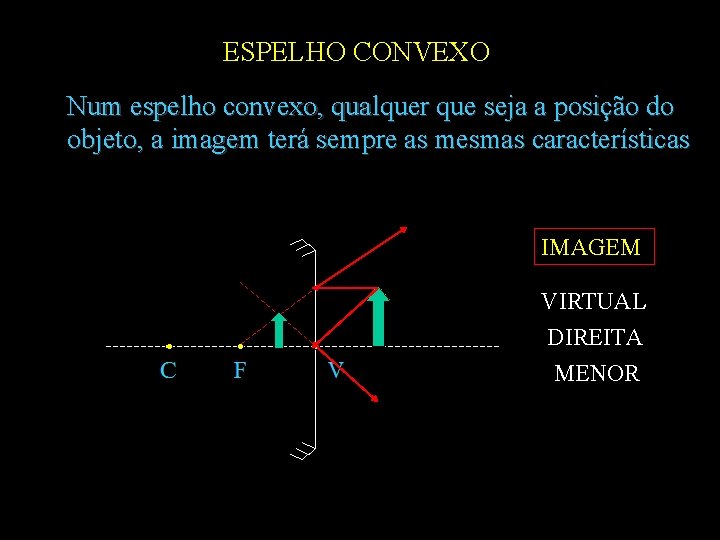
ESPELHO CONVEXO Num espelho convexo, qualquer que seja a posição do objeto, a imagem terá sempre as mesmas características IMAGEM VIRTUAL DIREITA MENOR

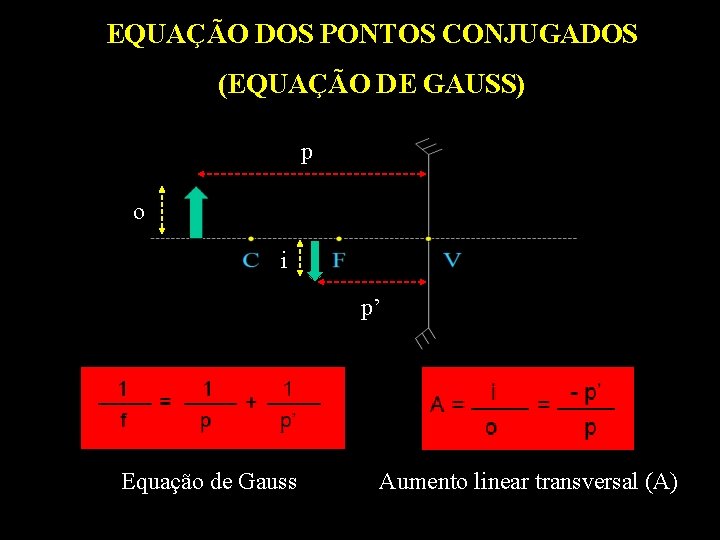
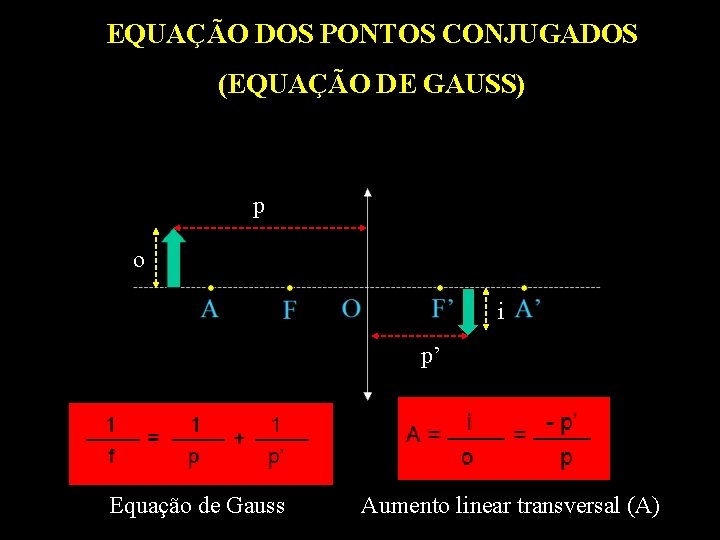
EQUAÇÃO DOS PONTOS CONJUGADOS (EQUAÇÃO DE GAUSS) p o i p’ Equação de Gauss Aumento linear transversal (A)

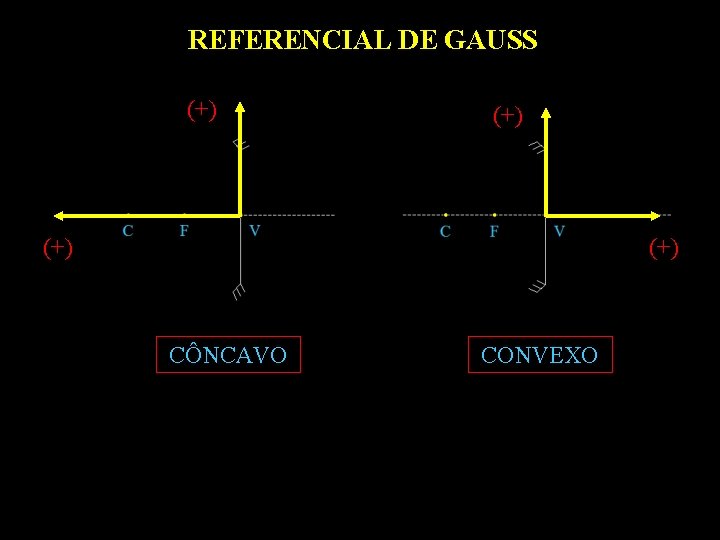
REFERENCIAL DE GAUSS (+) (+) CÔNCAVO CONVEXO

APLICAÇÕES - UFBA a) HOLOFOTE / FORNO SOLAR F

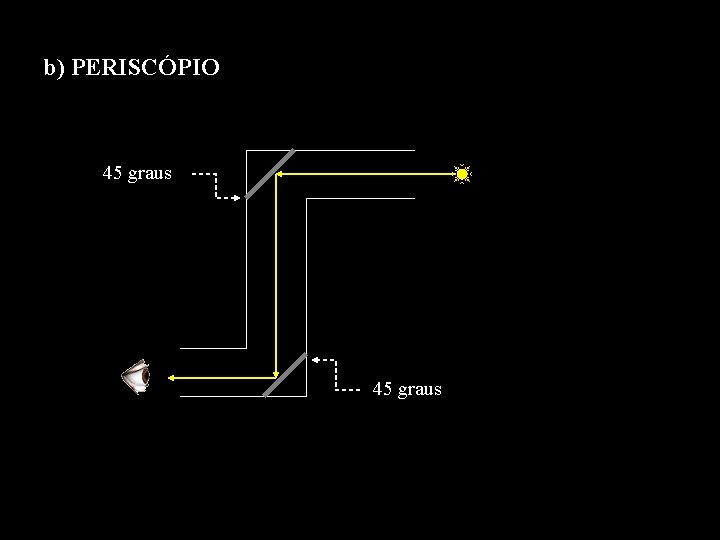
b) PERISCÓPIO 45 graus

EXERCÍCIOS 01. (Uneb) Um objeto é colocado a 15 cm de um espelho esférico côncavo, de raio de curvatura igual a 10 cm. A imagem conjugada do objeto pelo espelho se formará a uma distância deste igual a: a) 2, 5 cm b) 5, 0 cm c) 7, 5 cm d) 8, 6 cm e) 9, 4 cm

02. Um espelho esférico conjuga, de um objeto situado a 30 cm dele, uma imagem direita e três vezes menor que o objeto. Determine: a) o tipo de espelho; b) sua distância focal 03. (UNIVASF) Um espelho côncavo de raio de curvatura de 10 cm conjuga uma imagem real a 4 cm de seu vértice. Quanto ao objeto, pode-se afirmar que é a) real e está a 20 cm do vértice do espelho b) virtual e está a 20 cm do vértice do espelho c) real e está a 20/3 cm do vértice do espelho d) real e está a 20/9 cm do vértice do espelho e) real e está a 10/3 cm do vértice do espelho

UFBA 2007 – QUESTÃO 14 (04) A câmara fotográfica usada como visão do robô, constituída essencialmente de uma câmara escura provida de uma lente — a objetiva — e do filme, forma uma imagem real de um objeto sobre o filme. UFBA 2007 – QUESTÃO 16 (16) A ampliação da imagem conjugada de um dente por um espelho odontológico, de raio de curvatura igual a 4, 0 cm, colocado a 1, 0 cm de distância desse dente, é igual ao dobro do tamanho do dente observado.

REFRAÇÃO LUMINOSA 01. DEFINIÇÃO “Mudança de meio associado a uma mudança de velocidade” Refração com desvio Refração sem desvio (incidência oblíqua) (incidência normal)

02. ÍNDICE DE REFRAÇÃO DE UM MEIO (n) “Grandeza física que relaciona a velocidade da luz no vácuo e a velocidade da luz no meio em questão” velocidade da luz no vácuo velocidade da luz no meio em questão n é adimensional CONSIDERAÇÕES n > 1 nvácuo = 1 c > v

OBSERVAÇÕES a) O índice de refração é inversamente proporcional à velocidade de propagação da luz no meio Exemplo n. A > n. B v. A < v. B meio A mais refringente em relação ao meio B b) O índice de refração de um meio depende da natureza da luz que incide sobre ele c) O índice de refração depende da densidade do meio. maior densidade Menor velocidade maior índice(n)

EXEMPLOS 01. (UFBA) Um feixe de luz monocromática, cuja velocidade no vácuo é de 3 x 108 m/s, incide perpendicularmente em uma lâmina transparente e espessa de índice de refração igual a 1, 50. Determine a espessura da lâmina, sabendo-se que a luz gasta 1 x 10 -10 s para atravessa-la. Expresse o resultado em 10 -3 m. 02. O índice de refração absoluto da água é 4/3 e o do vidro é 3/2. Determine: a) o índice de refração da água em relação ao vidro b) a relação entre a velocidade da luz no vidro e a velocidade da luz na água

03. LEIS DA REFRAÇÃO LUMINOSA N RI i A B r RR 1ª LEI RI, RR e N são coplanares 2ª LEI n. A. sen i = n. B. sen r (Lei de Snell – Descartes)

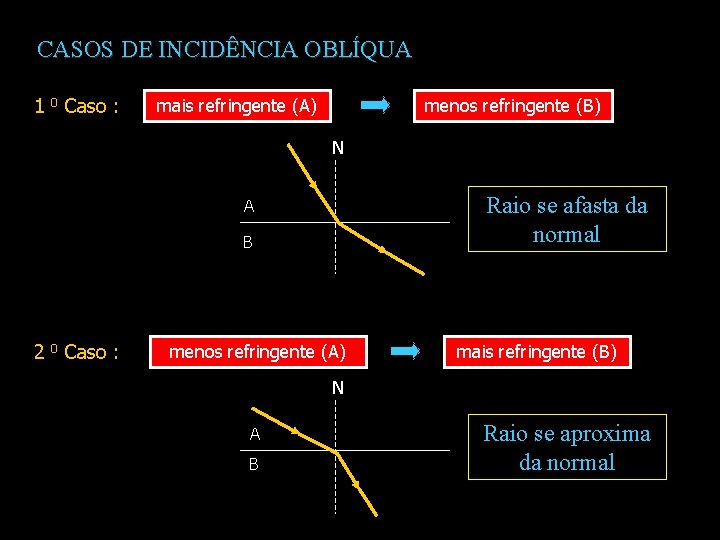
CASOS DE INCIDÊNCIA OBLÍQUA 1 0 Caso : mais refringente (A) menos refringente (B) N Raio se afasta da normal A B 2 0 Caso : menos refringente (A) mais refringente (B) N A B Raio se aproxima da normal

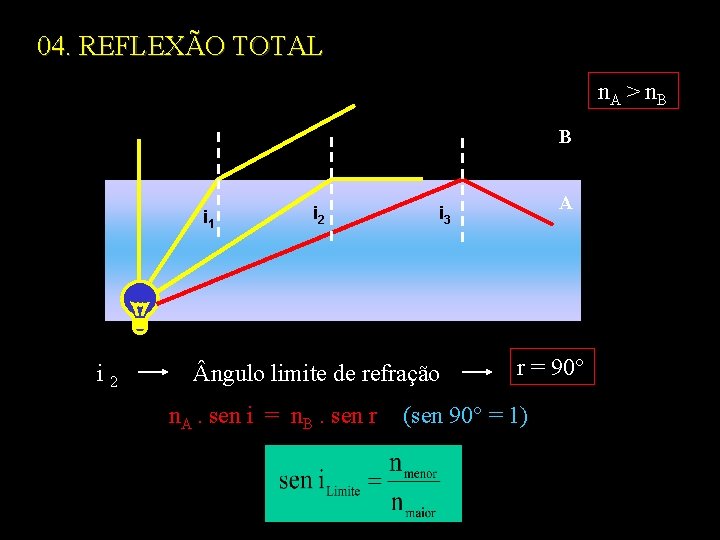
04. REFLEXÃO TOTAL n. A > n. B B i 1 i 2 ngulo limite de refração n. A. sen i = n. B. sen r A i 3 r = 90° (sen 90° = 1)

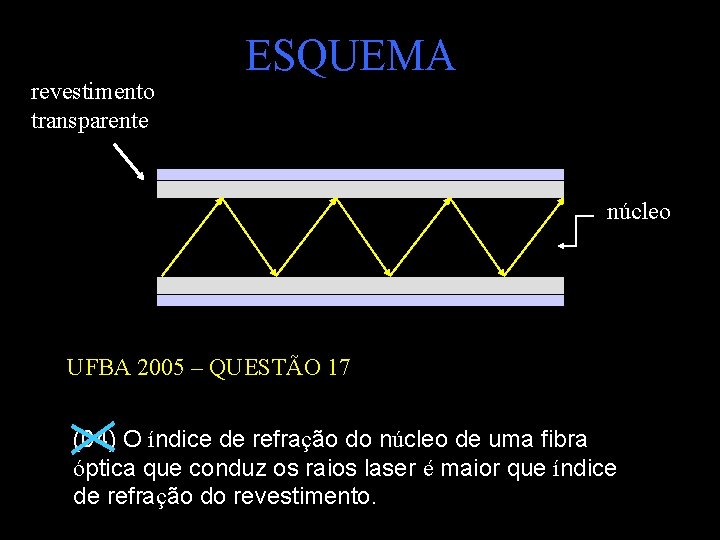
CONDIÇÕES - REFLEXÃO TOTAL 1ª CONDIÇÃO 2ª CONDIÇÃO mais refringente menos refringente ângulo de incidência > ângulo limite FIBRA ÓPTICA Filamento de vidro ou plástico, capaz de transmitir ondas eletromagnéticas através de reflexões totais, reduzindo ao máximo as perdas de energia por absorção

revestimento transparente ESQUEMA núcleo UFBA 2005 – QUESTÃO 17 (04) O índice de refração do núcleo de uma fibra óptica que conduz os raios laser é maior que índice de refração do revestimento.

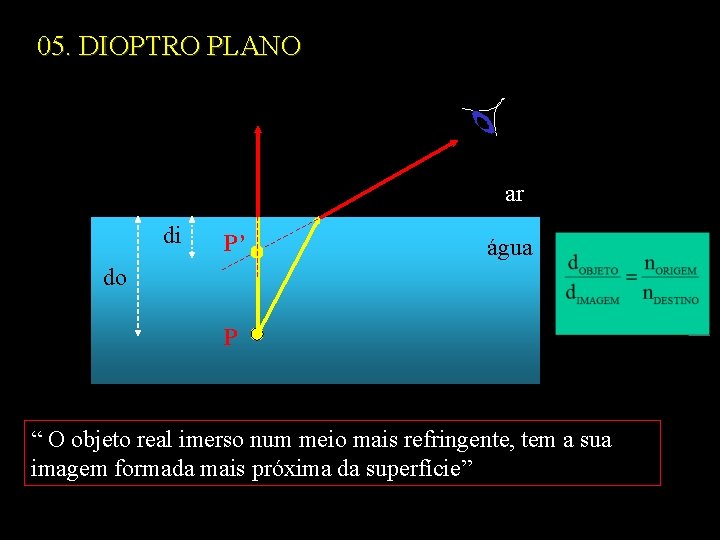
05. DIOPTRO PLANO ar di P’ água do P “ O objeto real imerso num meio mais refringente, tem a sua imagem formada mais próxima da superfície”

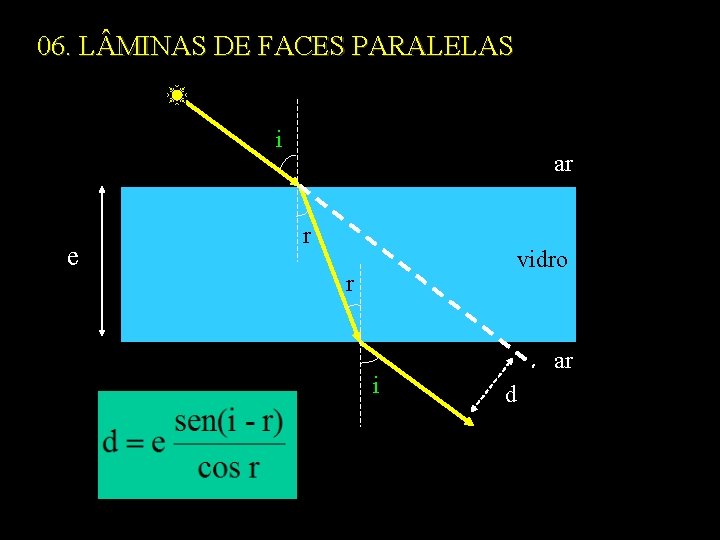
06. L MINAS DE FACES PARALELAS i e ar r vidro r i ar d

07. LENTES ESFÉRICAS DELGADAS BORDOS FINOS BICONVEXA PLANO-CONVEXA CÔNCAVO-CONVEXA BORDOS ESPESSOS BICÔNCAVA PLANO-CÔNCAVA CONVEXO-CÔNCAVA

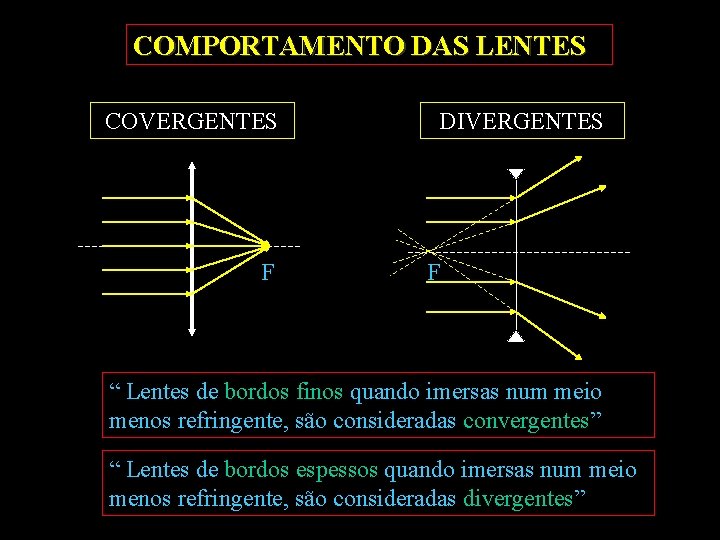
COMPORTAMENTO DAS LENTES COVERGENTES F DIVERGENTES F “ Lentes de bordos finos quando imersas num meio menos refringente, são consideradas convergentes” “ Lentes de bordos espessos quando imersas num meio menos refringente, são consideradas divergentes”

ELEMENTOS DE UMA LENTE f A f F f O f F’ A’ Eixo principal Centro Óptico(O): Ponto de coincidência dos vértices de uma lente delgada. Pontos Antiprincipais(A e A’): Ponto sobre o eixo principal onde AF = FO / A’F’ = F’O Distância Focal(f): Distância AF ou FO.

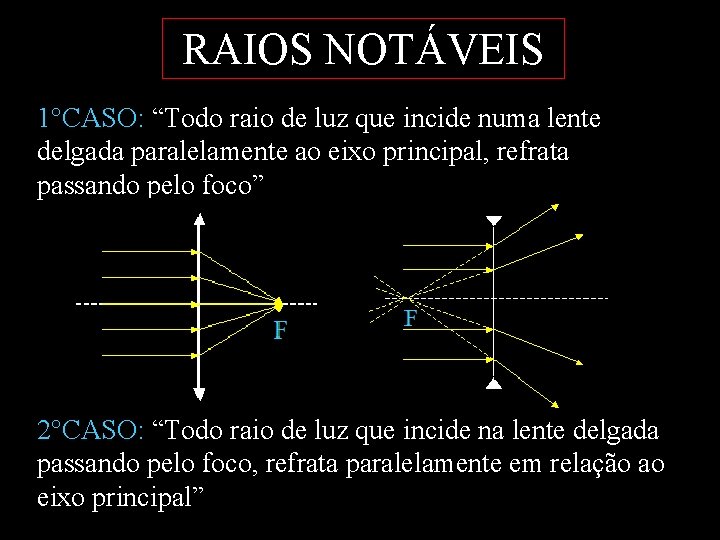
RAIOS NOTÁVEIS 1°CASO: “Todo raio de luz que incide numa lente delgada paralelamente ao eixo principal, refrata passando pelo foco” 2°CASO: “Todo raio de luz que incide na lente delgada passando pelo foco, refrata paralelamente em relação ao eixo principal”

3°CASO: “Todo raio de luz que incide na lente delgada passando pelo ponto antiprincipal, refrata passando pelo outro ponto principal”

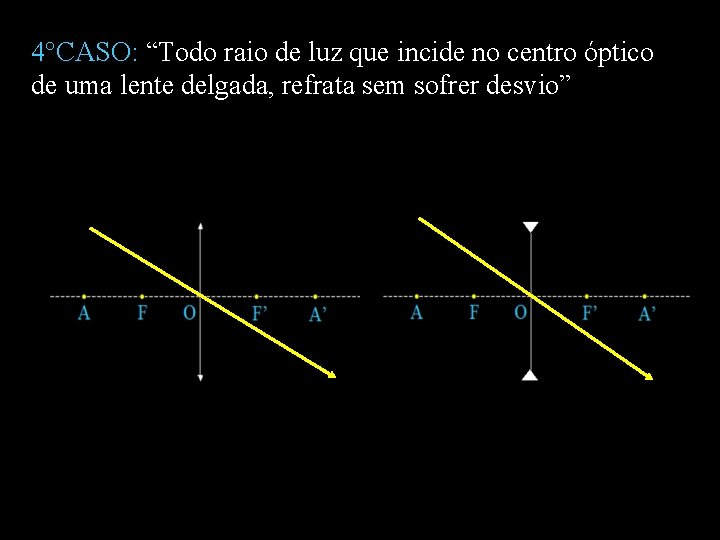
4°CASO: “Todo raio de luz que incide no centro óptico de uma lente delgada, refrata sem sofrer desvio”

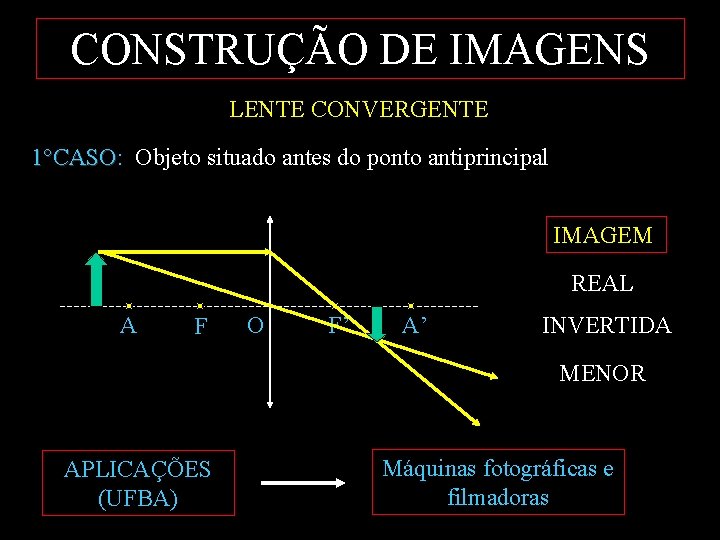
CONSTRUÇÃO DE IMAGENS LENTE CONVERGENTE 1°CASO: Objeto situado antes do ponto antiprincipal 1°CASO IMAGEM REAL A F O F’ A’ INVERTIDA MENOR APLICAÇÕES (UFBA) Máquinas fotográficas e filmadoras

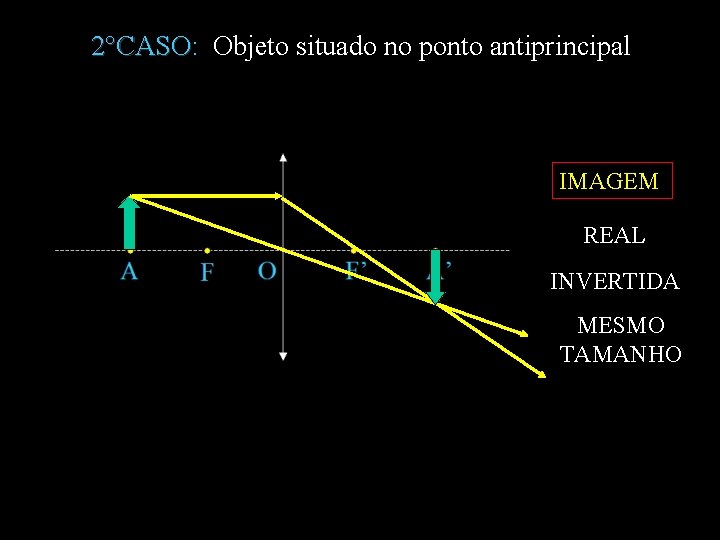
2°CASO: Objeto situado no ponto antiprincipal 2°CASO IMAGEM REAL INVERTIDA MESMO TAMANHO

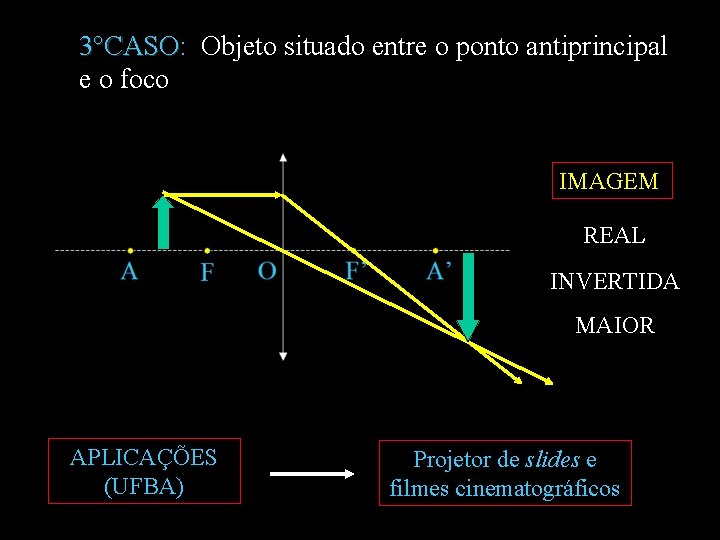
3°CASO: Objeto situado entre o ponto antiprincipal 3°CASO e o foco IMAGEM REAL INVERTIDA MAIOR APLICAÇÕES (UFBA) Projetor de slides e filmes cinematográficos

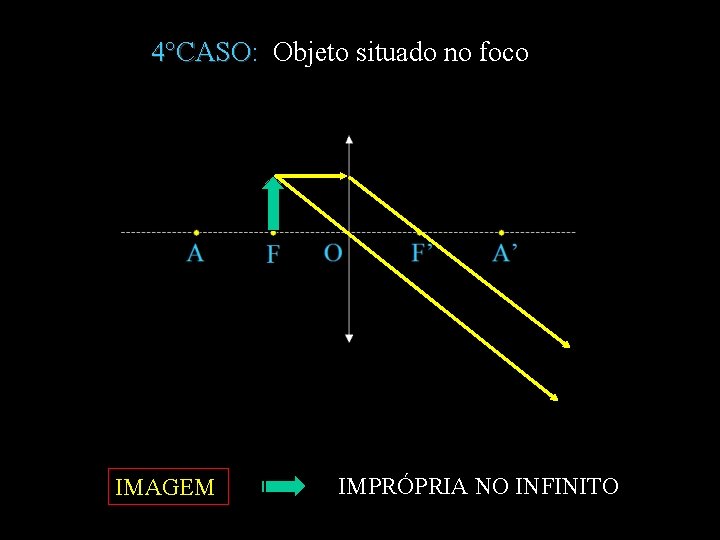
4°CASO: Objeto situado no foco 4°CASO IMAGEM IMPRÓPRIA NO INFINITO

5°CASO: Objeto situado entre o foco e o vértice 5°CASO IMAGEM VIRTUAL DIREITA MAIOR APLICAÇÕES (UFBA) Lupas e Lentes de aumento

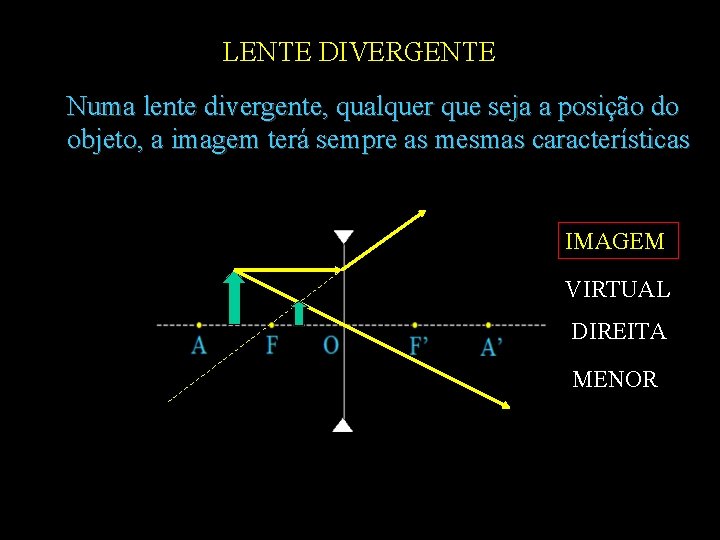
LENTE DIVERGENTE Numa lente divergente, qualquer que seja a posição do objeto, a imagem terá sempre as mesmas características IMAGEM VIRTUAL DIREITA MENOR

EQUAÇÃO DOS PONTOS CONJUGADOS (EQUAÇÃO DE GAUSS) p o i p’ Equação de Gauss Aumento linear transversal (A)

REFERENCIAL DE GAUSS (+) p’ (+) COVERGENTES DIST NCIA FOCAL (f) p (+) p’ (+) DIVERGENTE CONVERGENTE f > 0 DIVERGENTE f < 0

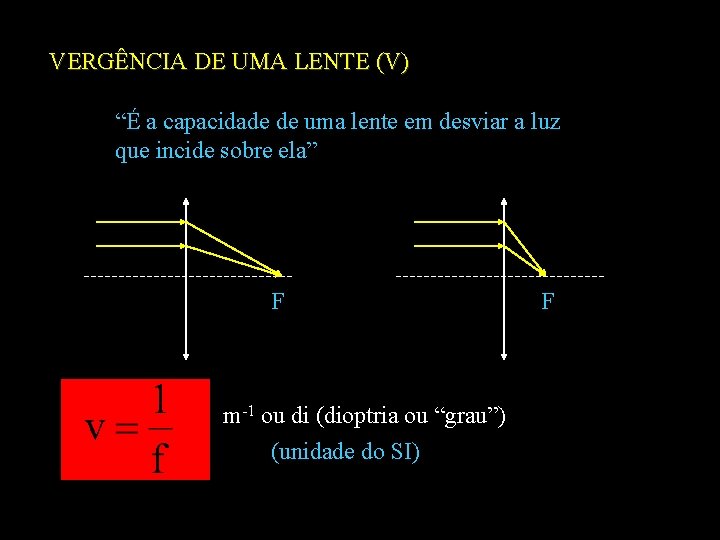
VERGÊNCIA DE UMA LENTE (V) “É a capacidade de uma lente em desviar a luz que incide sobre ela” F m-1 ou di (dioptria ou “grau”) (unidade do SI) F

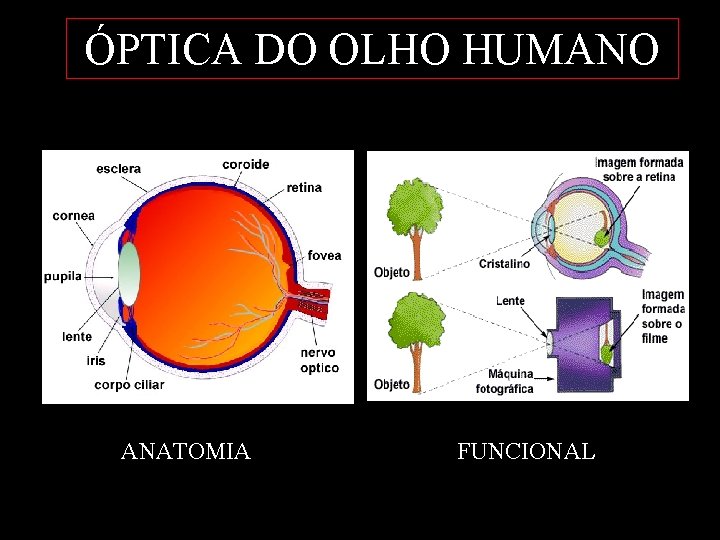
ÓPTICA DO OLHO HUMANO ANATOMIA FUNCIONAL

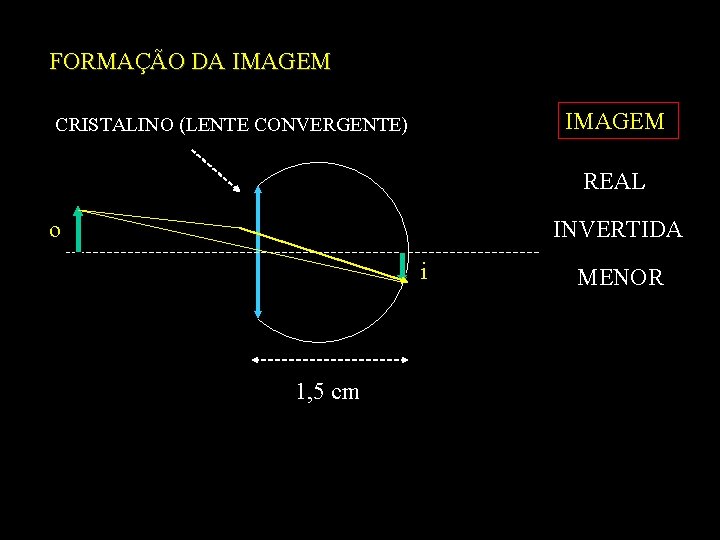
FORMAÇÃO DA IMAGEM CRISTALINO (LENTE CONVERGENTE) REAL o INVERTIDA i 1, 5 cm MENOR

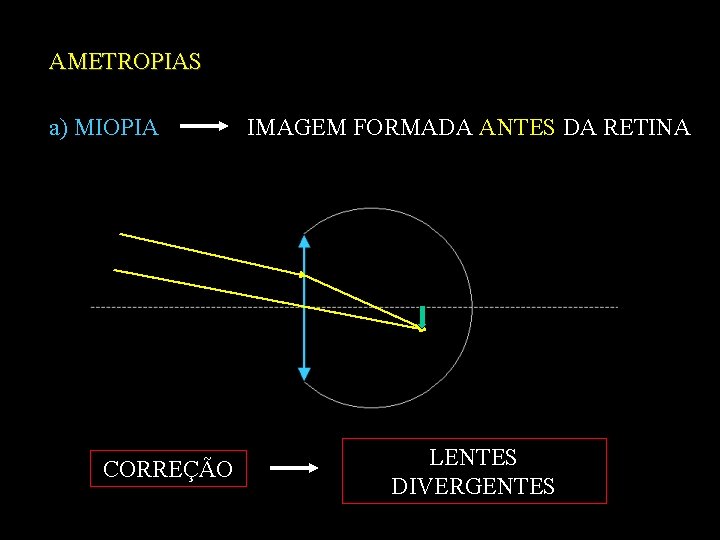
AMETROPIAS a) MIOPIA CORREÇÃO IMAGEM FORMADA ANTES DA RETINA LENTES DIVERGENTES

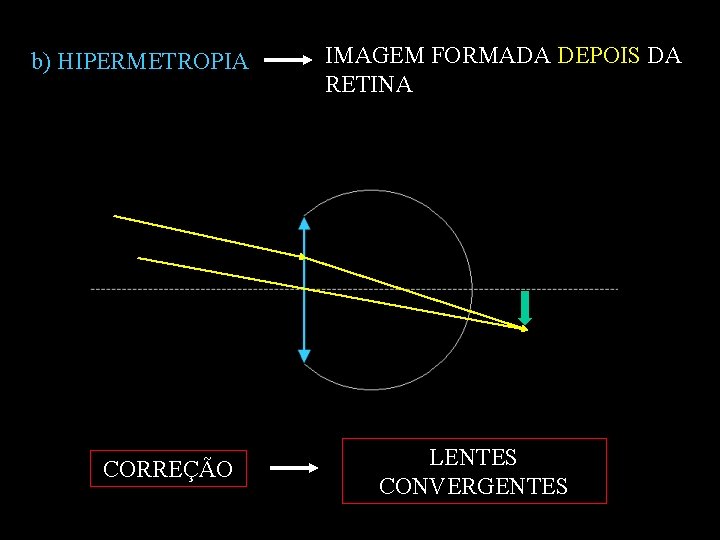
b) HIPERMETROPIA CORREÇÃO IMAGEM FORMADA DEPOIS DA RETINA LENTES CONVERGENTES

c) Astigmatismo Anomalia em que a córnea ou cristalino, não se apresenta como uma calota esférica d) Estrabismo Disfunção dos músculos que prendem o globo ocular. e) Daltonismo