PSY 307 Statistics for the Behavioral Sciences Chapter

PSY 307 – Statistics for the Behavioral Sciences Chapter 6 – Correlation

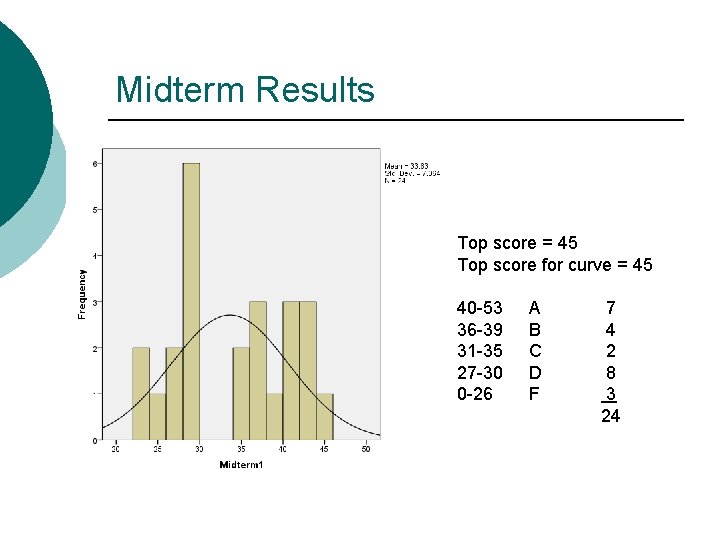
Midterm Results Top score = 45 Top score for curve = 45 40 -53 36 -39 31 -35 27 -30 0 -26 A B C D F 7 4 2 8 3 24

Aleks/Holcomb Hint ¡

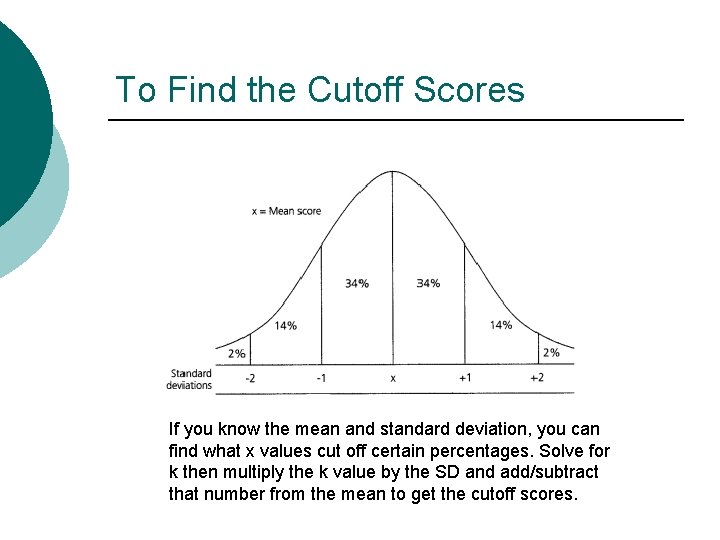
To Find the Cutoff Scores If you know the mean and standard deviation, you can find what x values cut off certain percentages. Solve for k then multiply the k value by the SD and add/subtract that number from the mean to get the cutoff scores.

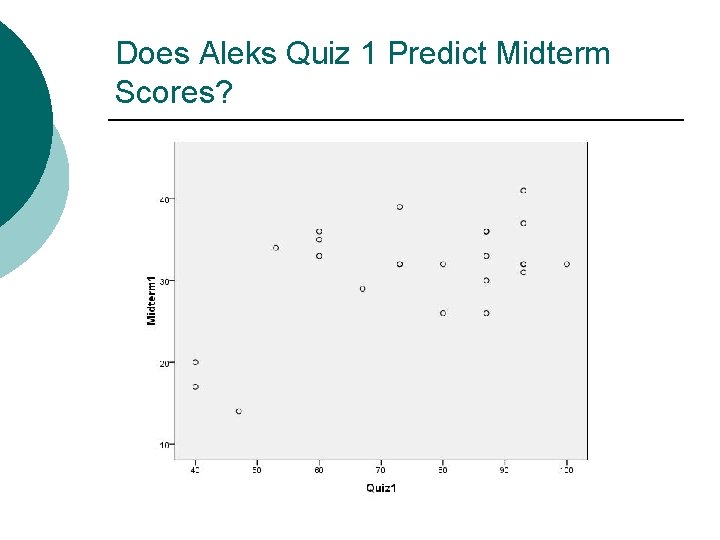
Does Aleks Quiz 1 Predict Midterm Scores?

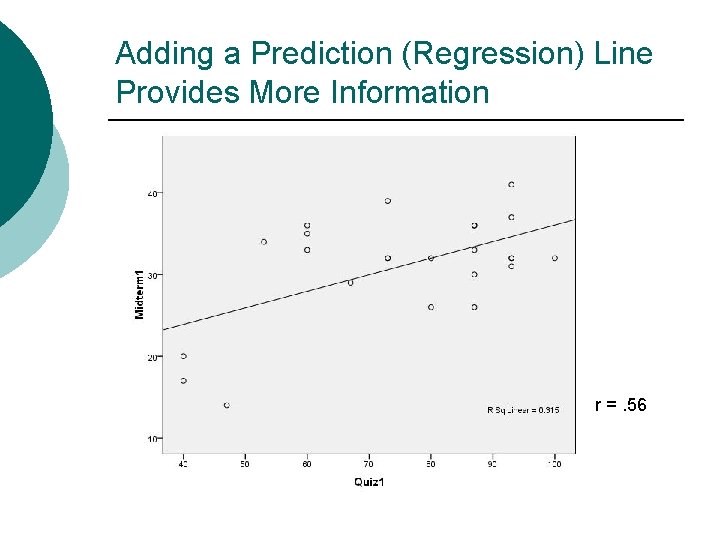
Adding a Prediction (Regression) Line Provides More Information r =. 56

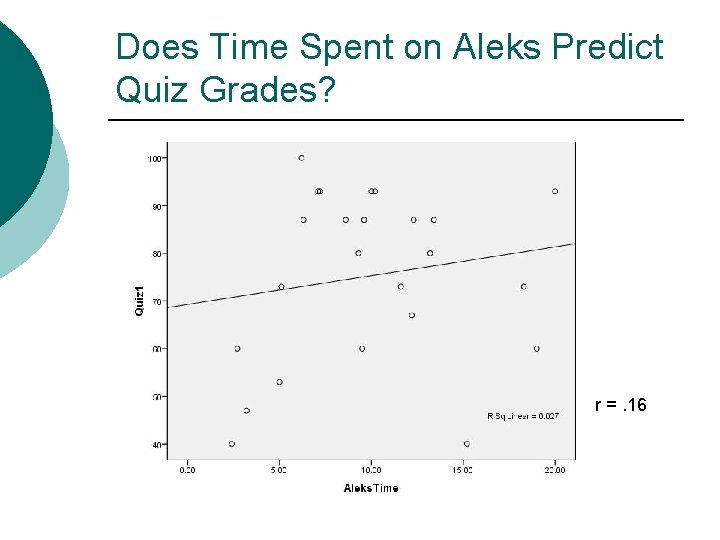
Does Time Spent on Aleks Predict Quiz Grades? r =. 16

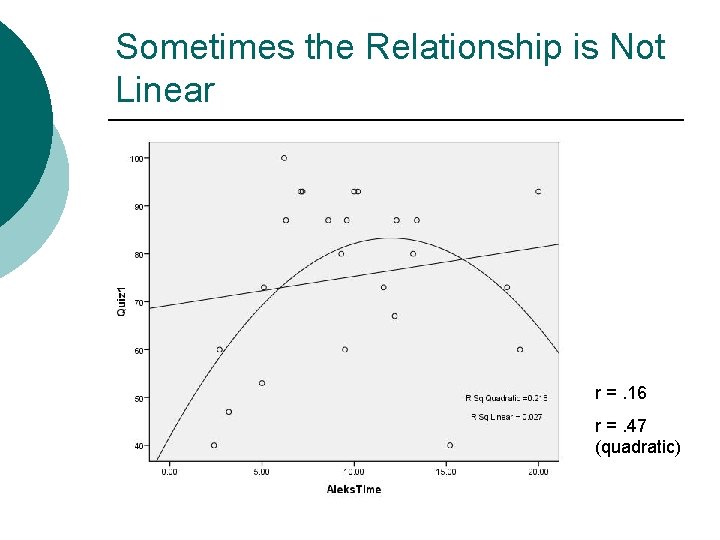
Sometimes the Relationship is Not Linear r =. 16 r =. 47 (quadratic)

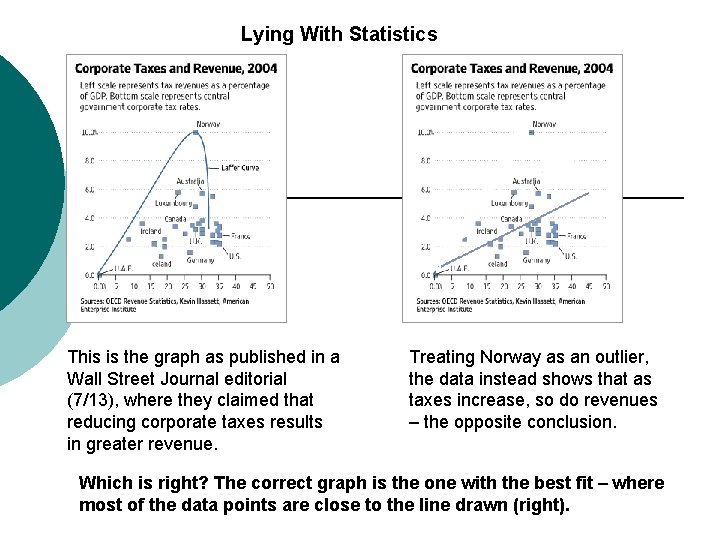
Lying With Statistics This is the graph as published in a Wall Street Journal editorial (7/13), where they claimed that reducing corporate taxes results in greater revenue. Treating Norway as an outlier, the data instead shows that as taxes increase, so do revenues – the opposite conclusion. Which is right? The correct graph is the one with the best fit – where most of the data points are close to the line drawn (right).

Describing Relationships Positive relationship – high values tend to go with high values, low with low. ¡ Negative relationship – high values tend to go with low values, low with high. ¡ No relationship – no regularity appears between pairs of scores in two distributions. ¡

Relationship Does Not Imply Causality ¡ A relationship can exist without being a CAUSAL relationship. l Correlation does not imply causation. Third variable problem -- a third variable is causing both of the variables you are measuring to change – e. g. , popsicles & drowning. ¡ The direction of causality cannot be determined from the r statistic. ¡

Chocolate and Nobel Prizes ¡ http: //www. nejm. org/doi/full/10. 10 56/NEJMon 1211064

Scatterplots One variable is measured on the x-axis, the other on the y-axis. ¡ Positive relationship – a cluster of dots sloping upward from the lower left to the upper right. ¡ Negative relationship – a cluster of dots sloping down from upper left to lower right. ¡ No relationship – no apparent slope. ¡

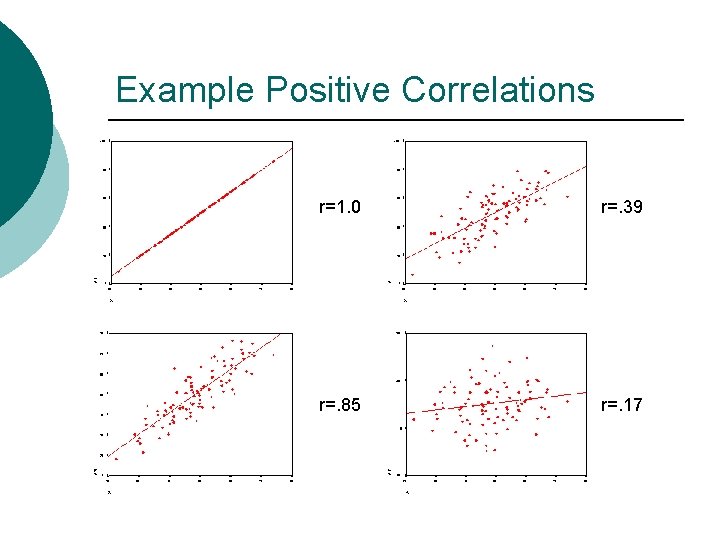
Example Positive Correlations r=1. 0 r=. 39 r=. 85 r=. 17

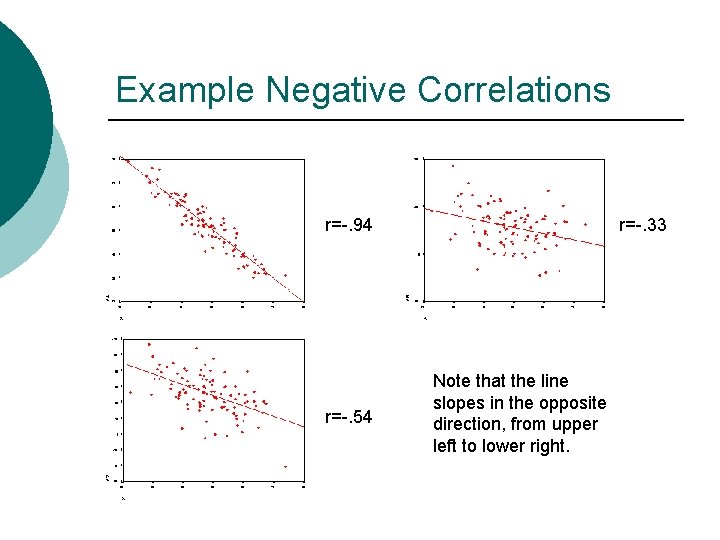
Example Negative Correlations r=-. 94 r=-. 54 r=-. 33 Note that the line slopes in the opposite direction, from upper left to lower right.

Strength of Relationship The more closely the dots approximate a straight line, the stronger the relationship. ¡ A perfect relationship forms a straight line. ¡ Dots forming a line reflect a linear relationship. ¡ Dots forming a curved or bent line reflect a curvilinear relationship. ¡

More Examples ¡ http: //www. stat. uiuc. edu/courses/stat 100/java/GCApplet. Frame. html

Correlation Coefficient ¡ Pearson’s r –a measure of how well a straight line describes the cluster of dots in a plot. l l l ¡ Ranges from -1 to 1. The sign indicates a positive or negative relationship. The value of r indicates strength of relationship. Pearson’s r is independent of units of measure.

Interpreting Pearson’s r ¡ The value of r needed to assert a strong relationship depends on: l l The size of n What is being measured. Pearson’s r is NOT the percent or proportion of a perfect relationship. ¡ Correlation is not causation. ¡ l Experimentation is used to confirm a suspected causal relationship.

Calculating Pearson’s r r = S zxzy _______ n – 1 This formula is most useful when the scores are already z-scores. ¡ Computational formulas – use whichever is most convenient for the data at hand. ¡

Sum of the Products (SP)

Computational Formulas

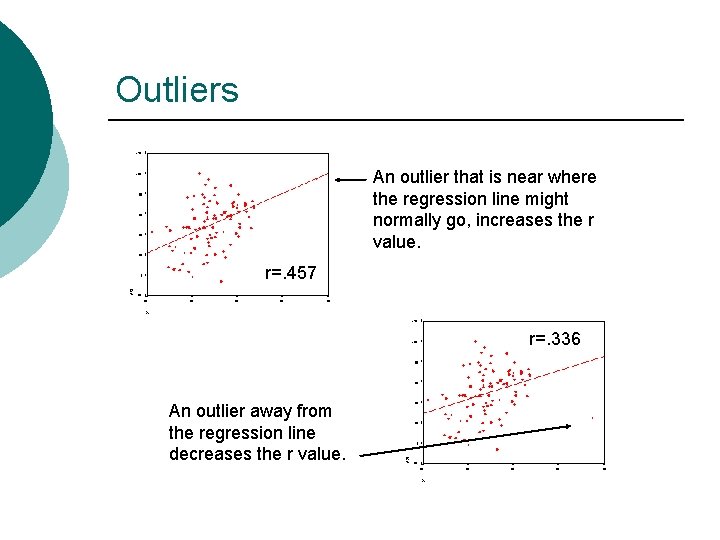
Outliers An outlier that is near where the regression line might normally go, increases the r value. r=. 457 r=. 336 An outlier away from the regression line decreases the r value.

Dealing with Outliers can dramatically change the value of the r correlation coefficient. ¡ Always produce a scatterplot and inspect for outliers before calculating r. ¡ Sometimes outliers can be omitted. ¡ Sometimes r cannot be used. ¡ ¡ http: //www. stat. sc. edu/~west/javahtml/Regression. html

Other Correlation Coefficients ¡ Spearman’s rho (r) – based on ranks rather than values. l Used with ordinal data (qualitative data that can be ordered least to most). Point biserial correlation -- correlations between quantitative data and two coded categories. ¡ Cramer’s phi – correlation between two ordered qualitative categories. ¡