PSC 2019 Computing Maximal Palindromes and Distinct Palindromes

PSC 2019 Computing Maximal Palindromes and Distinct Palindromes in a Trie Mitsuru Funakoshi, Yuto Nakashima, Shunsuke Inenaga, Hideo Bannai, Masayuki Takeda Kyushu University

Palindromes

Palindromes

Maximal palindromes in a string 7 9. 5

Distinct palindromes in a string

Distinct palindromes in a string

Distinct palindromes in a string

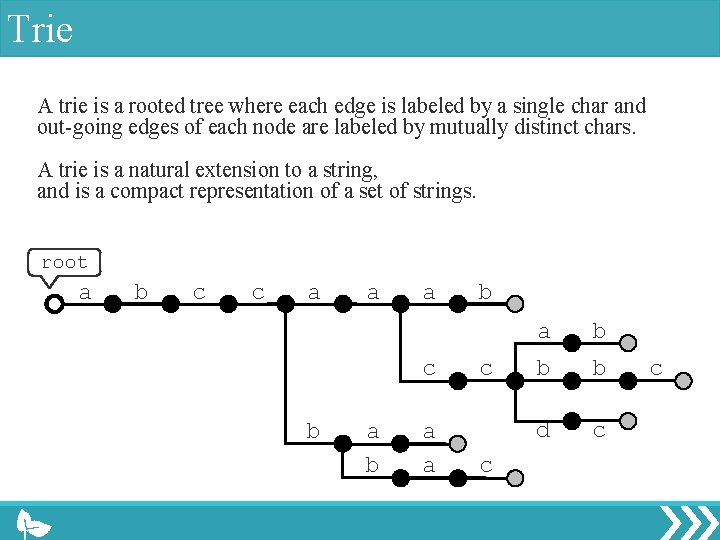
Trie A trie is a rooted tree where each edge is labeled by a single char and out-going edges of each node are labeled by mutually distinct chars. A trie is a natural extension to a string, and is a compact representation of a set of strings. root a b c c a a a c b a a b c c a b b b d c c

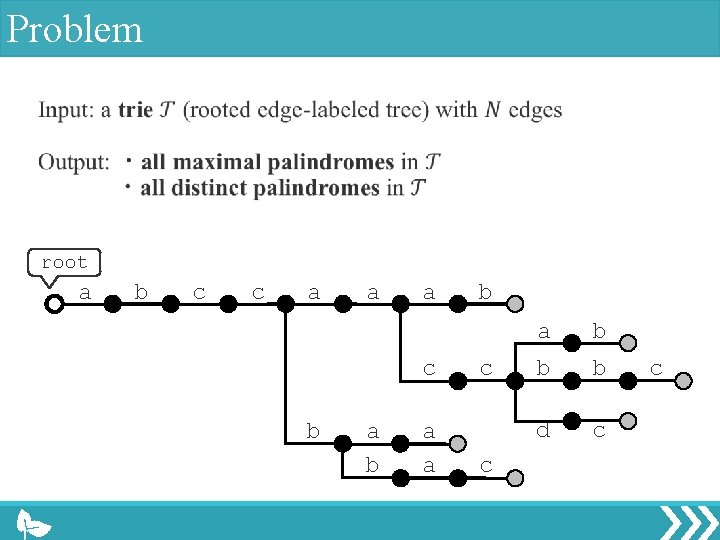
Problem root a b c c a a a c b a a b c c a b b b d c c

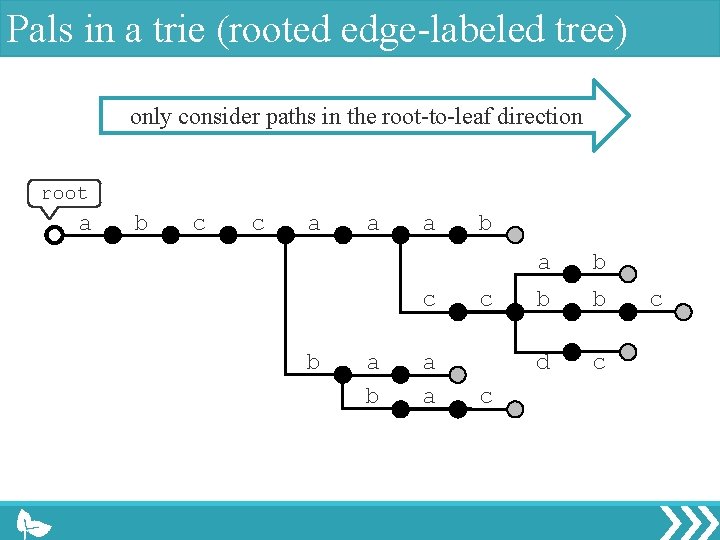
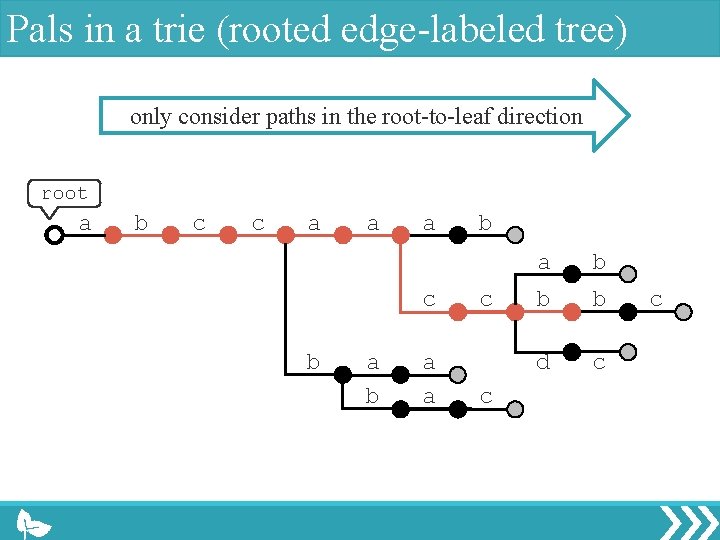
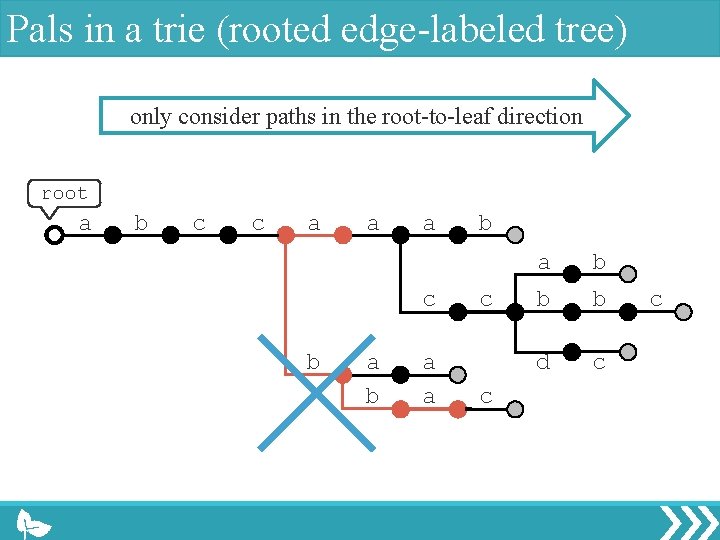
Pals in a trie (rooted edge-labeled tree) only consider paths in the root-to-leaf direction root a b c c a a a c b a a b c c a b b b d c c

Pals in a trie (rooted edge-labeled tree) only consider paths in the root-to-leaf direction root a b c c a a a c b a a b c c a b b b d c c

Pals in a trie (rooted edge-labeled tree) only consider paths in the root-to-leaf direction root a b c c a a a c b a a b c c a b b b d c c

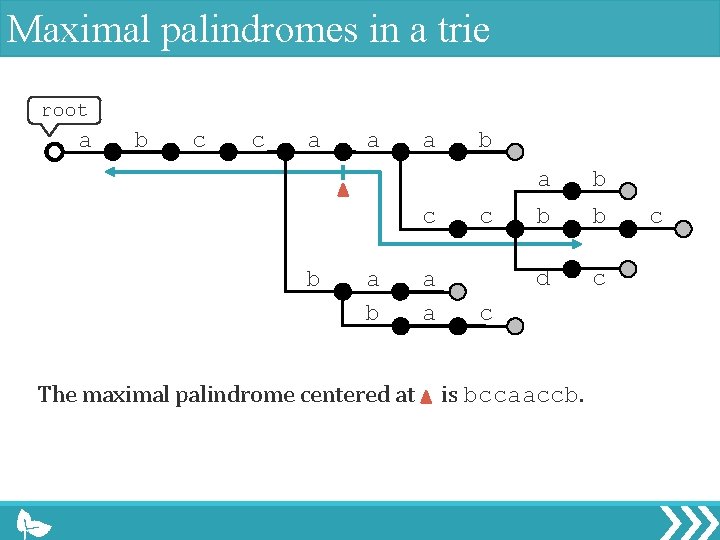
Maximal palindromes in a trie root a b c c a a a c b a b The maximal palindrome centered at a a b c a b b b d c c is bccaaccb. c

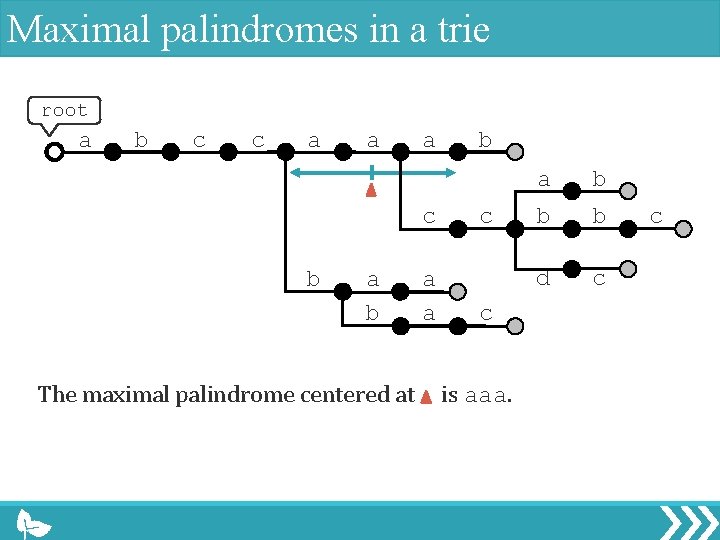
Maximal palindromes in a trie root a b c c a a a c b a b The maximal palindrome centered at a a b c c is aaa. a b b b d c c

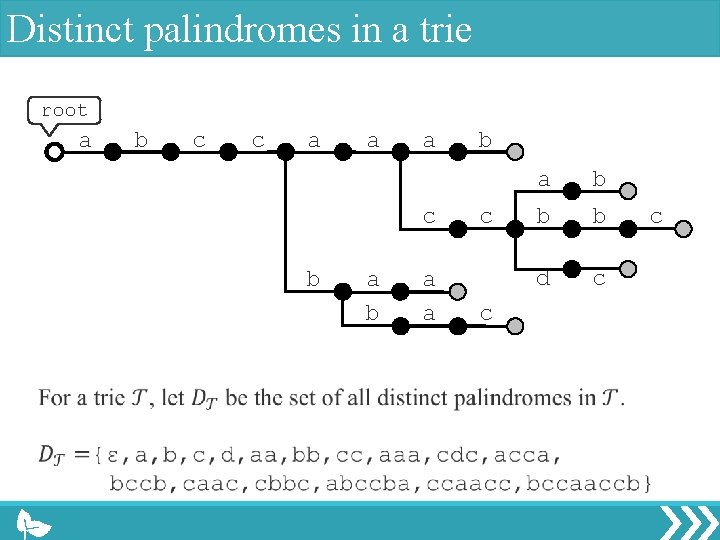
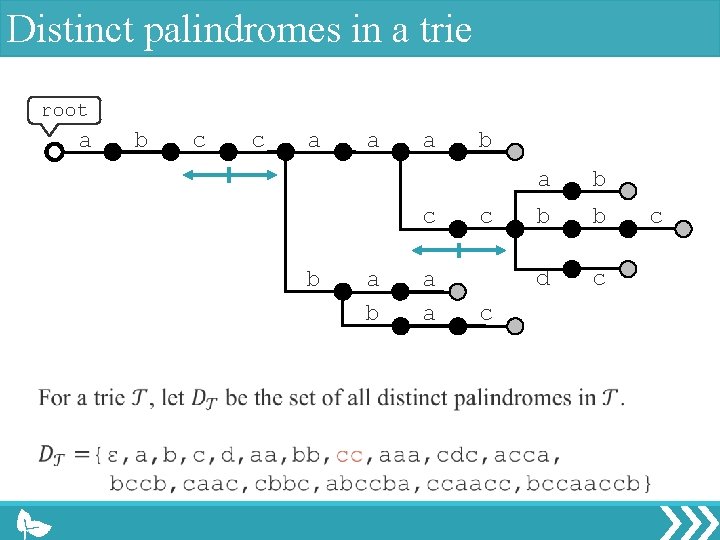
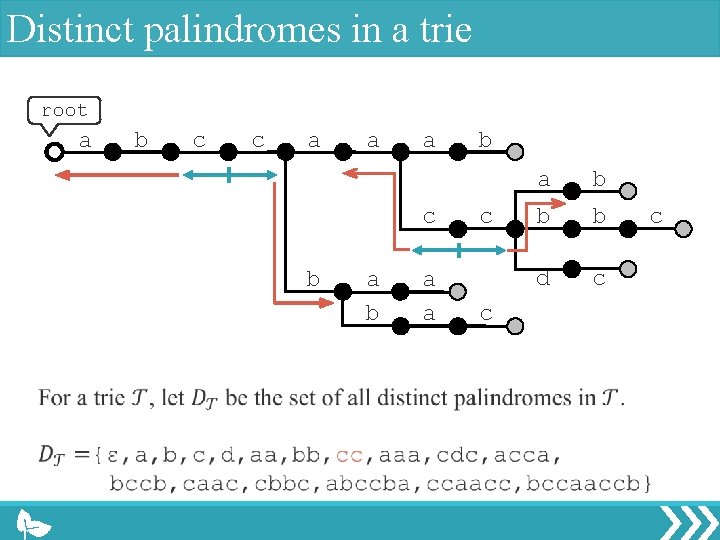
Distinct palindromes in a trie root a b c c a a a c b a a b c c a b b b d c c

Distinct palindromes in a trie root a b c c a a a c b a a b c c a b b b d c c

Distinct palindromes in a trie root a b c c a a a c b a a b c c a b b b d c c

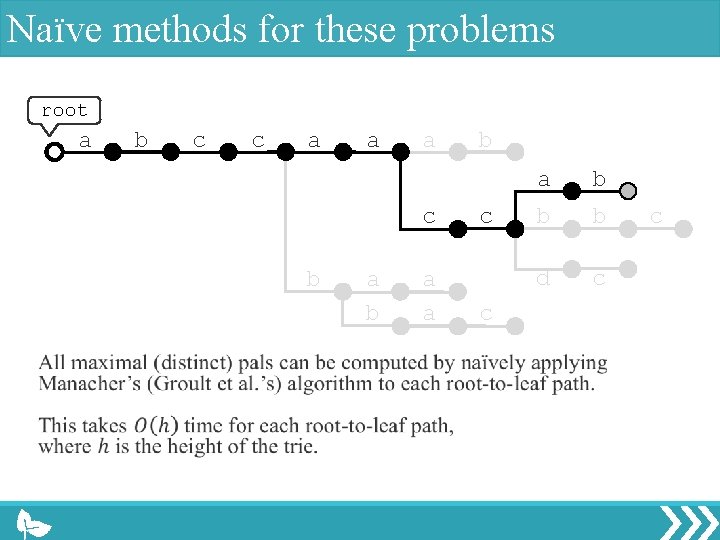
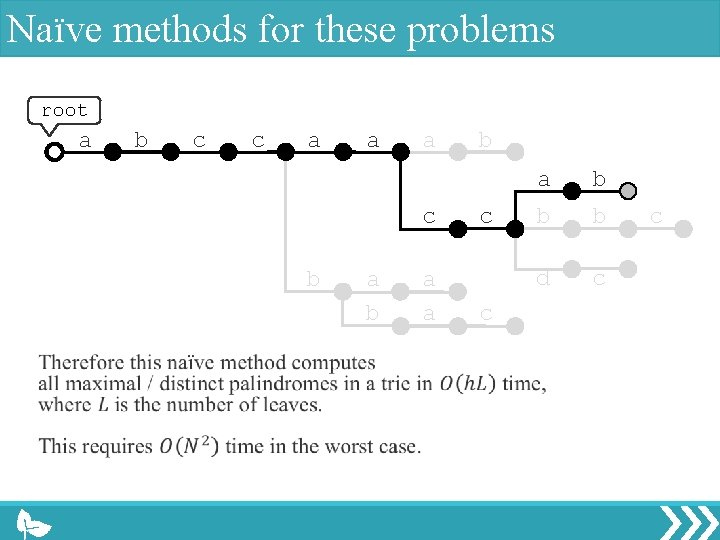
Naïve methods for these problems root a b c c a a a c b a a b c c a b b b d c c

Naïve methods for these problems root a b c c a a a c b a a b c c a b b b d c c

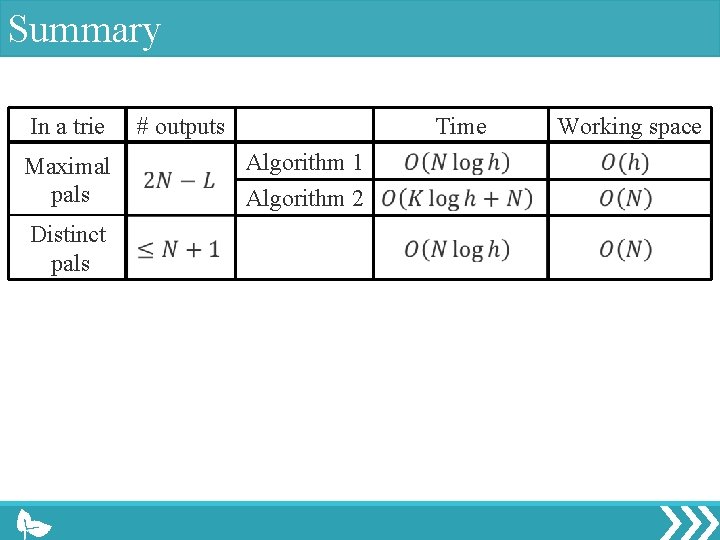
Main results for maximal palindromes # outputs In a trie In a string Time Algorithm 1 Algorithm 2 Manacher Working space

Main results for maximal palindromes # outputs In a trie In a string Time Algorithm 1 Algorithm 2 Manacher Working space

Main results for distinct palindromes # outputs In a trie In a string Time Groult et al. Working space

Main results In a trie Maximal pals Distinct pals # outputs Time Algorithm 1 Algorithm 2 Working space

Main results In a trie Maximal pals Distinct pals # outputs Time Algorithm 1 Algorithm 2 Working space

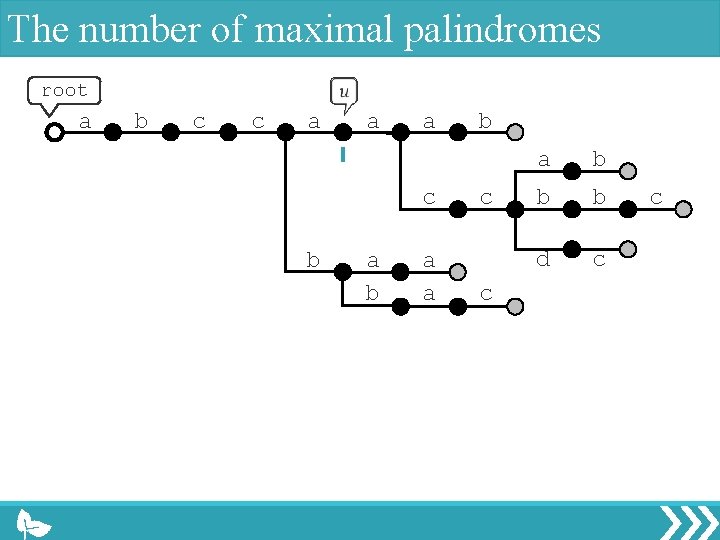
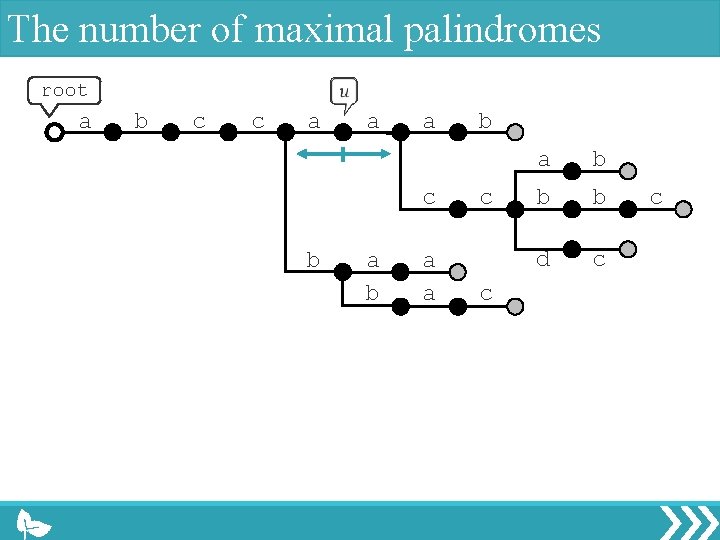
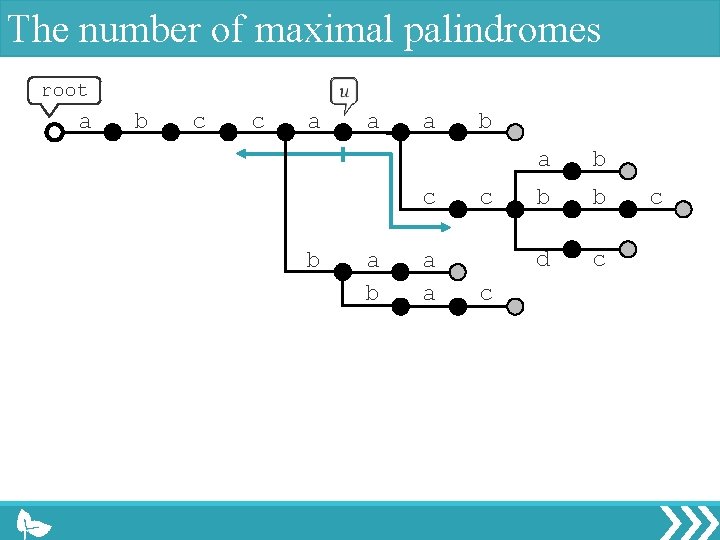
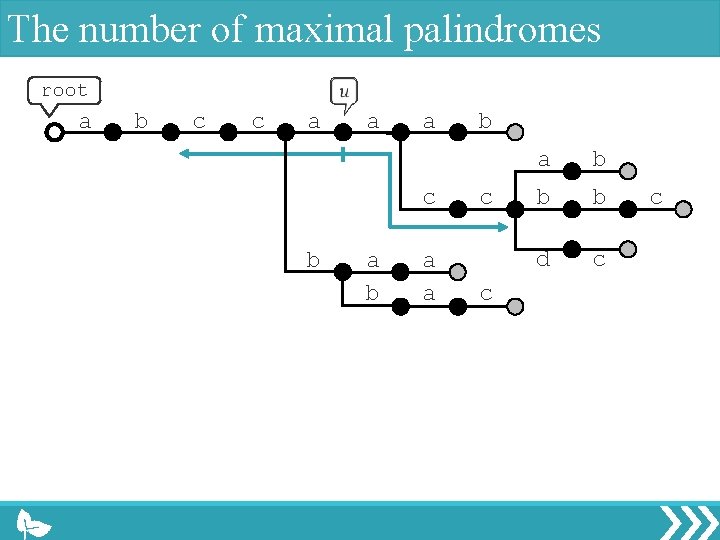
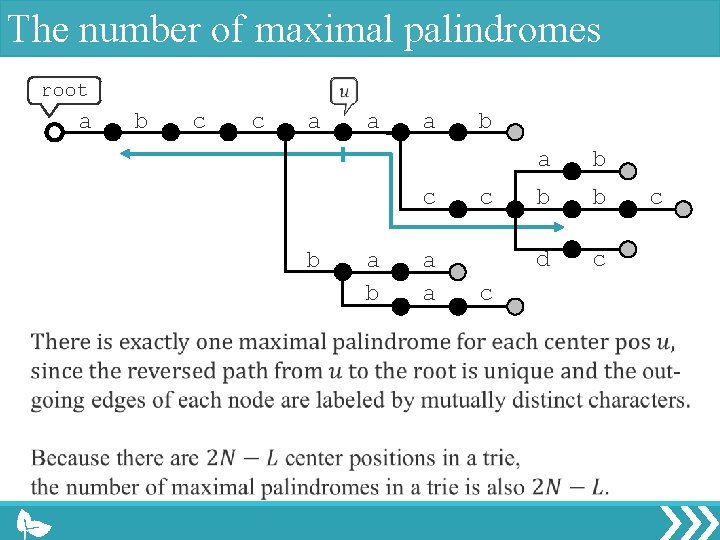
The number of maximal palindromes root a b c c a a a c b a a b c c a b b b d c c

The number of maximal palindromes root a b c c a a a c b a a b c c a b b b d c c

The number of maximal palindromes root a b c c a a a c b a a b c c a b b b d c c

The number of maximal palindromes root a b c c a a a c b a a b c c a b b b d c c

The number of maximal palindromes root a b c c a a a c b a b a a b c c a b b b d c c

Computing maximal palindromes In a trie Maximal pals Distinct pals # outputs Time Algorithm 1 Algorithm 2 Working space

Overview

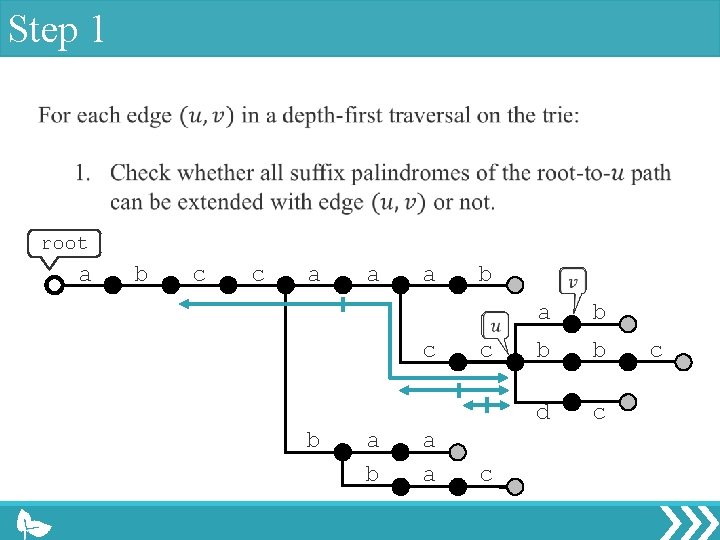
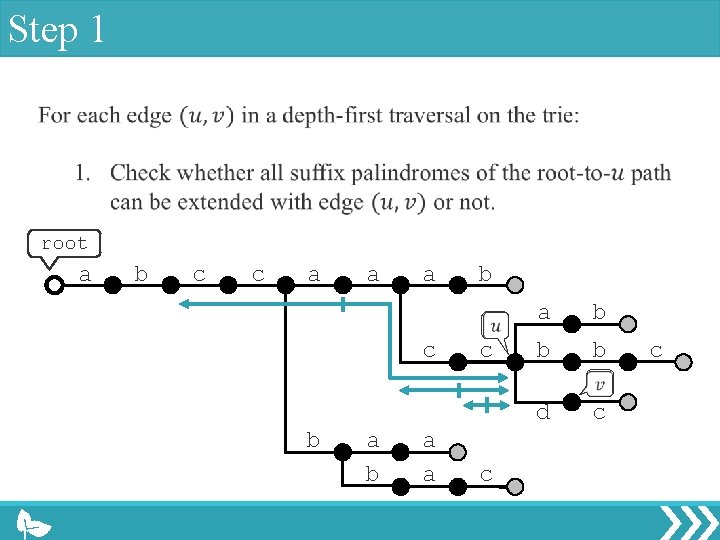
Step 1 root a b c c a a a c b a a b c c a b b b d c c

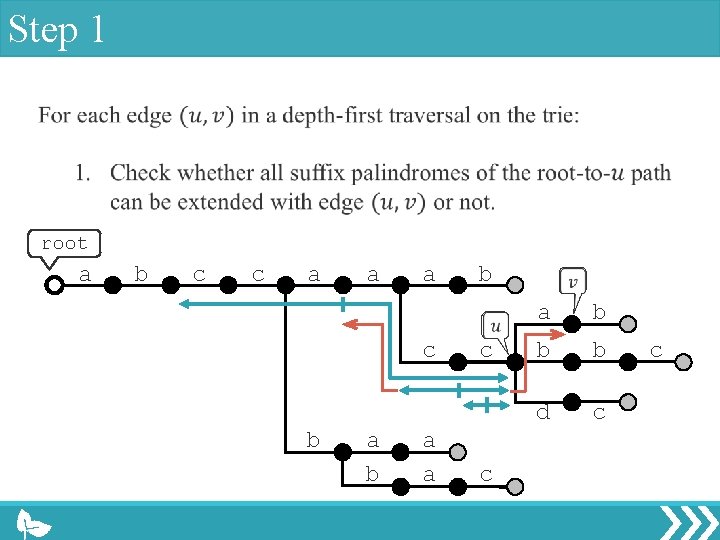
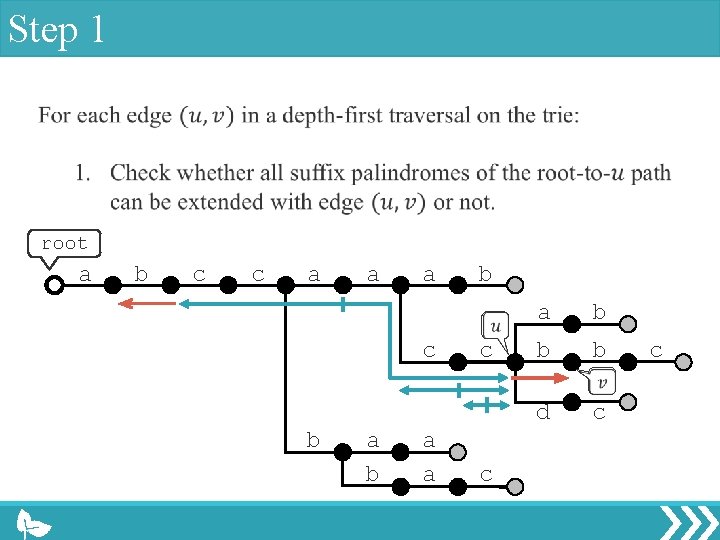
Step 1 root a b c c a a a c b a a b c c a b b b d c c

Step 1 root a b c c a a a c b c a b b b d b a a c c c

Step 1 root a b c c a a a c b c a b b b d b a a c c c

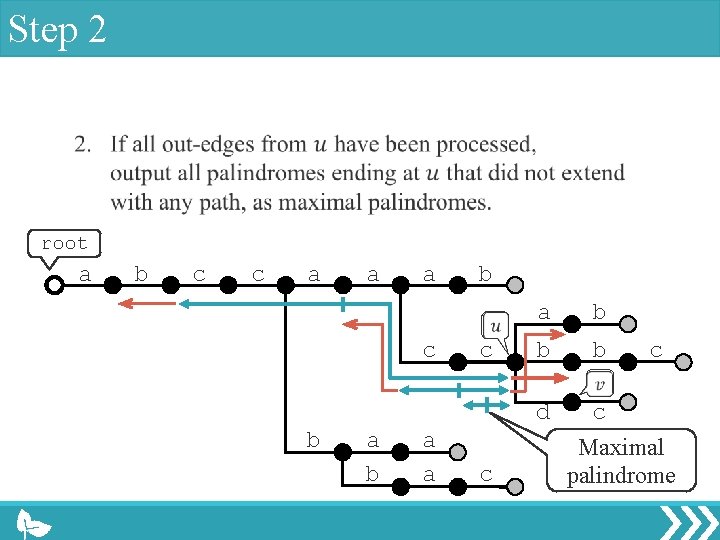
Step 2 root a b c c a a a c b c a b b b c d b a a c c Maximal palindrome

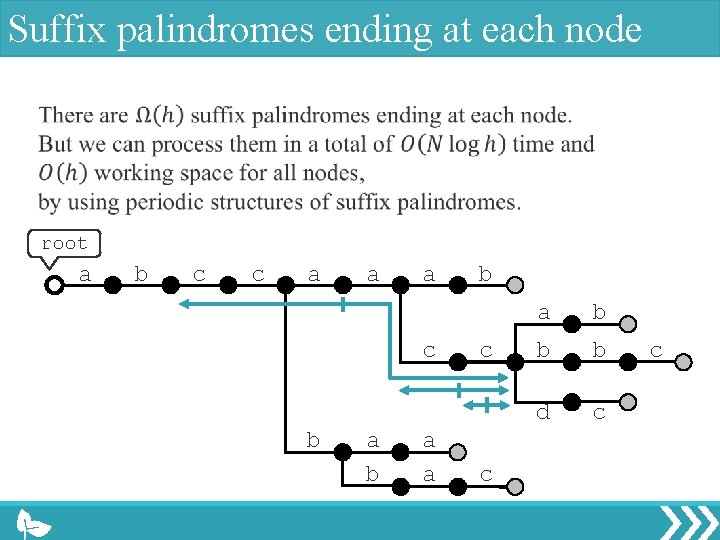
Suffix palindromes ending at each node root a b c c a a a c b a a b c c a b b b d c c

Periodic property of suffix pals in a str.

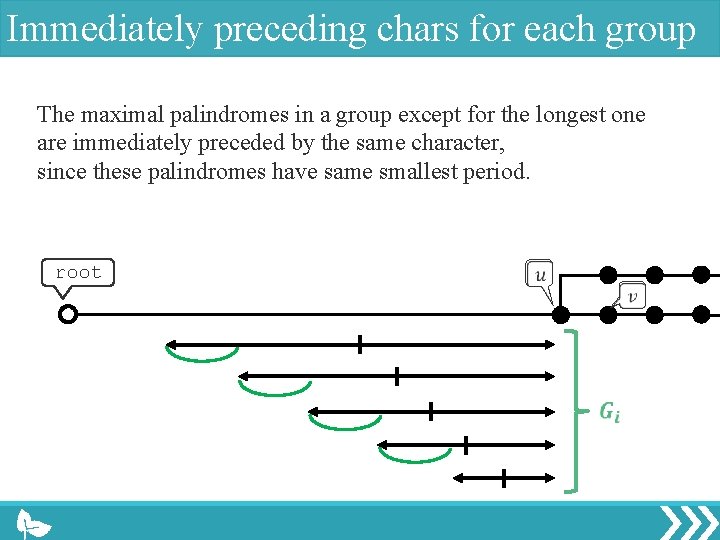
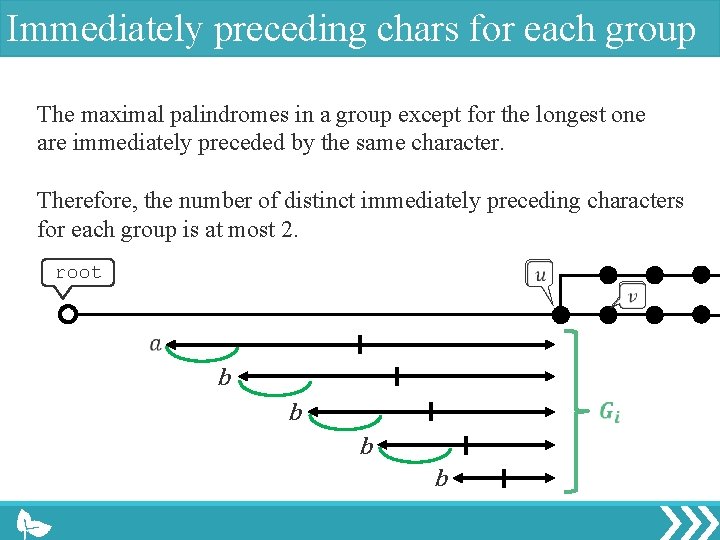
Immediately preceding chars for each group The maximal palindromes in a group except for the longest one are immediately preceded by the same character, since these palindromes have same smallest period. root

Immediately preceding chars for each group The maximal palindromes in a group except for the longest one are immediately preceded by the same character. Therefore, the number of distinct immediately preceding characters for each group is at most 2. root b b b b

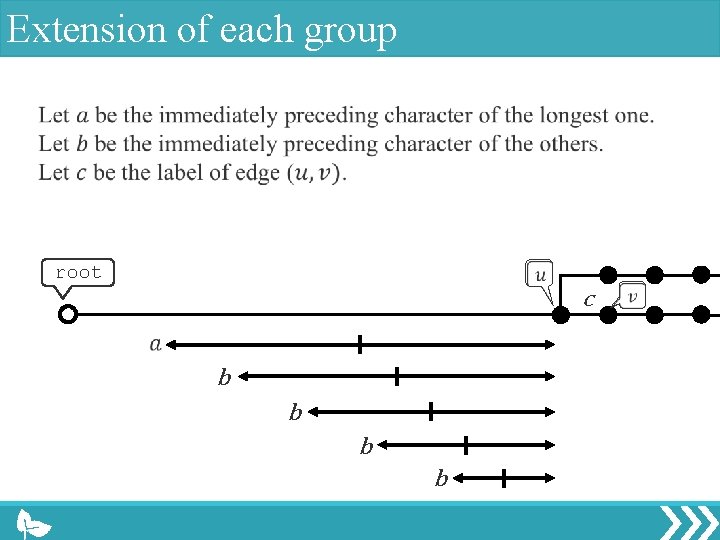
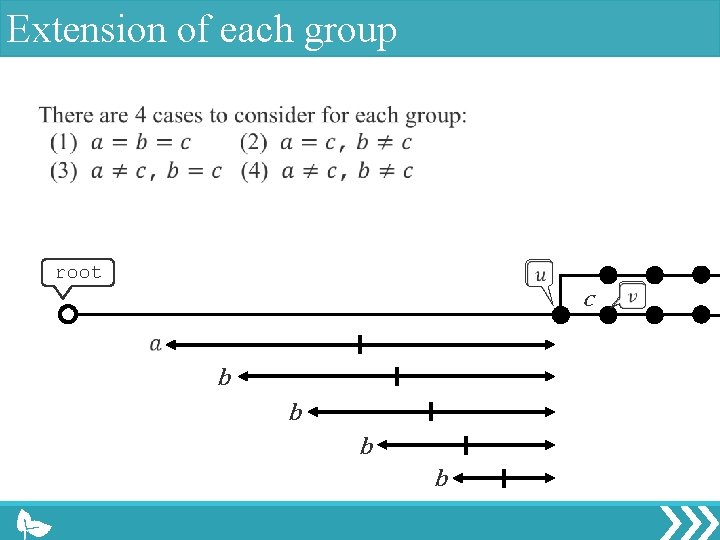
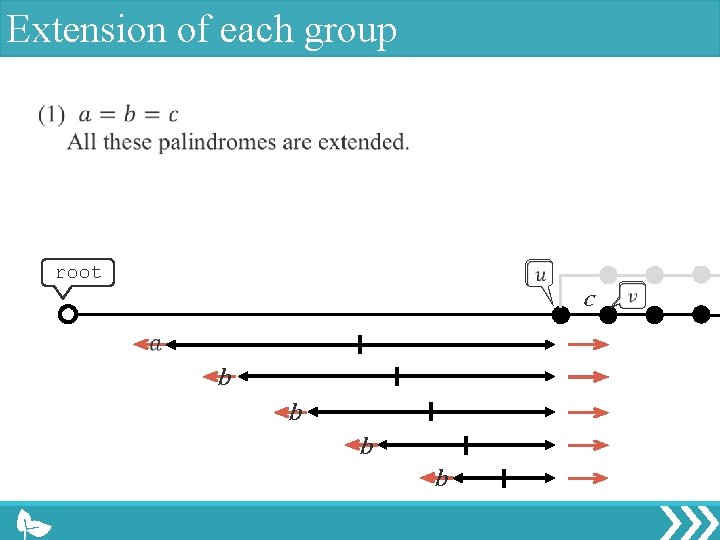
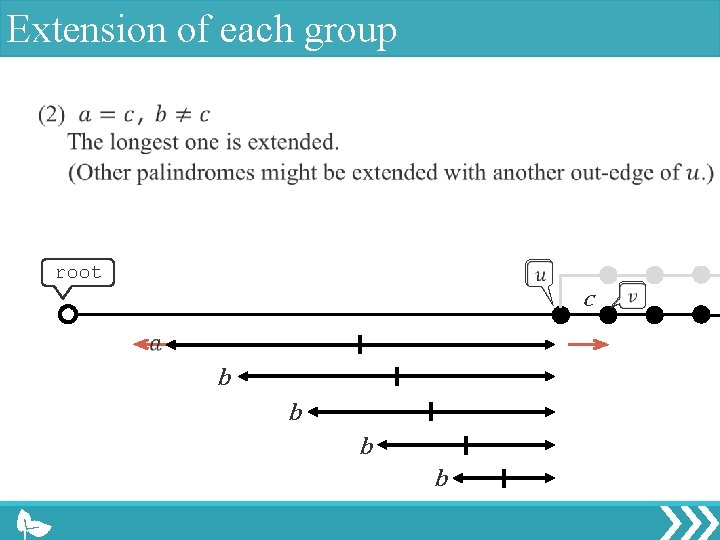
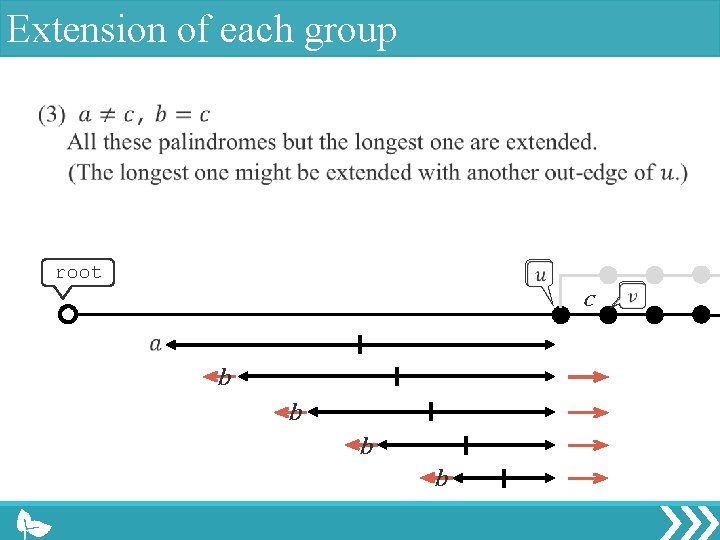
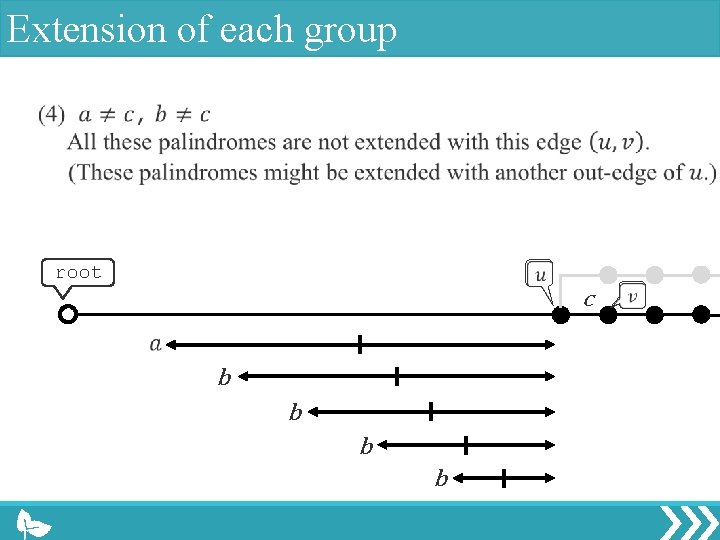
Extension of each group root c b b

Extension of each group root c b b

Extension of each group root c b b

Extension of each group root c b b

Extension of each group root c b b

Extension of each group root c b b

Running time

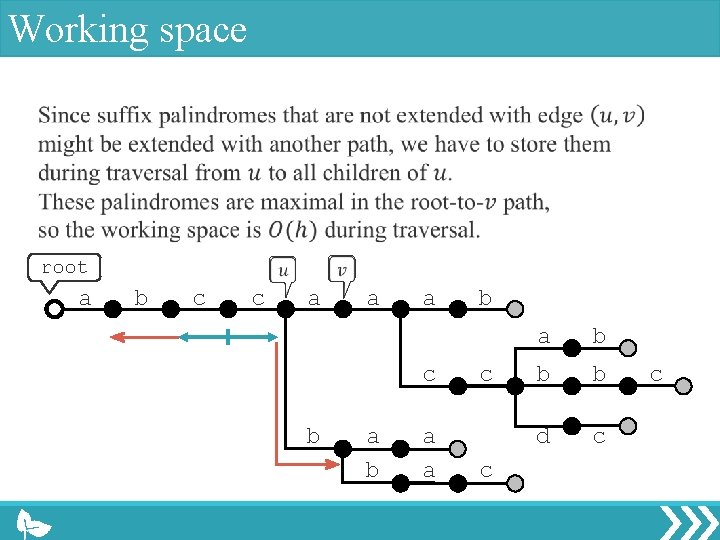
Working space root a b c c a a a c b a a b c c a b b b d c c

Summary In a trie Maximal pals Distinct pals # outputs Time Algorithm 1 Algorithm 2 Working space

Open problems

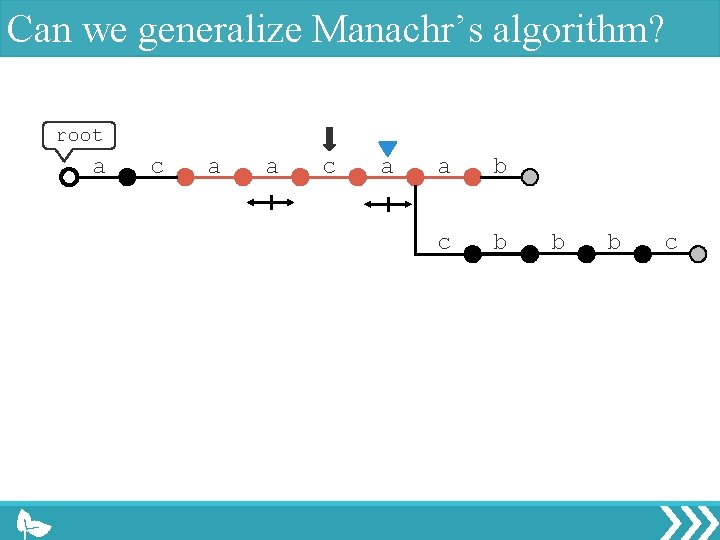
Can we generalize Manachr’s algorithm? root a c a a b c b b b c

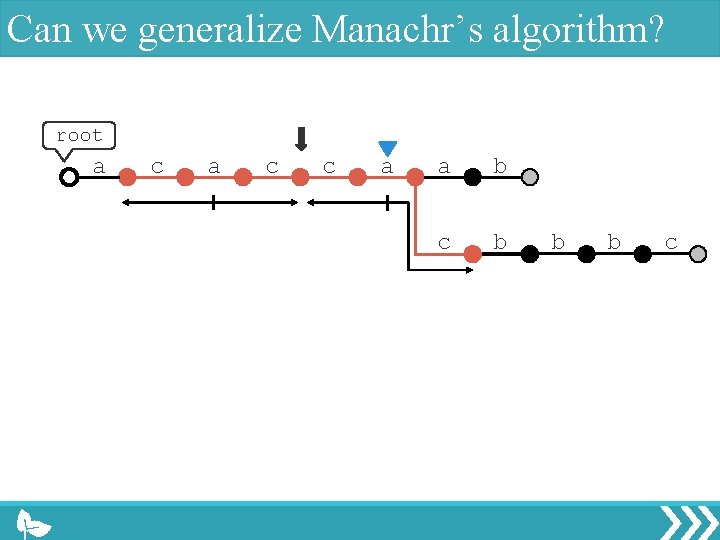
Can we generalize Manachr’s algorithm? root a c c a a b c b b b c

Previous work of palindromes in a tree To our knowledge, palindromes in a trie (rooted edge-labeled tree) have not been studied previously.

Periodic property of maximal palindromes

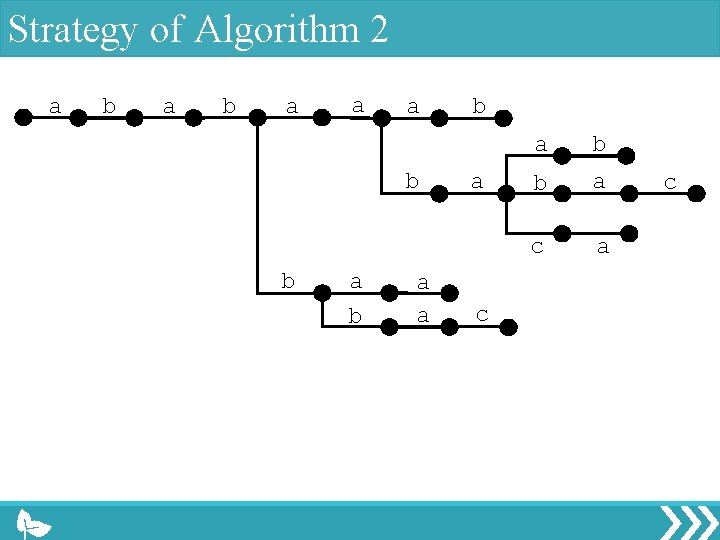
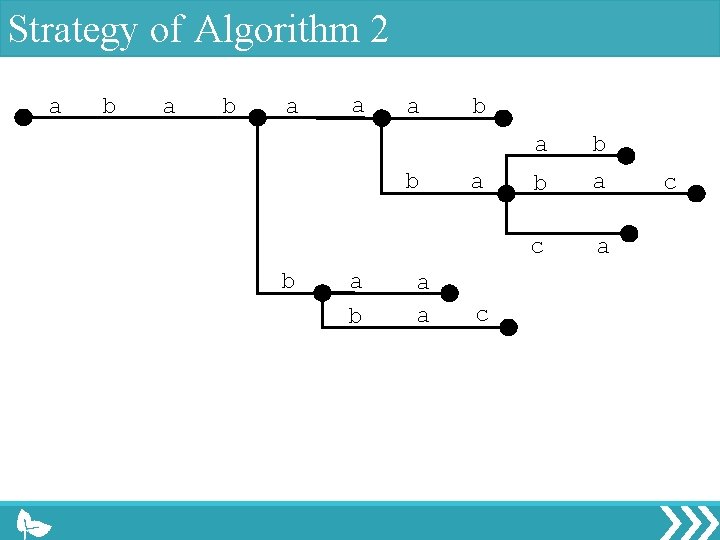
Strategy of Algorithm 2 a b a a a b b a a b a c a b b a c

Strategy of Algorithm 2 a b a a a b b a a b a c a b b a c

Strategy of Algorithm 2 a b a a a b b a a b a c a b b a c

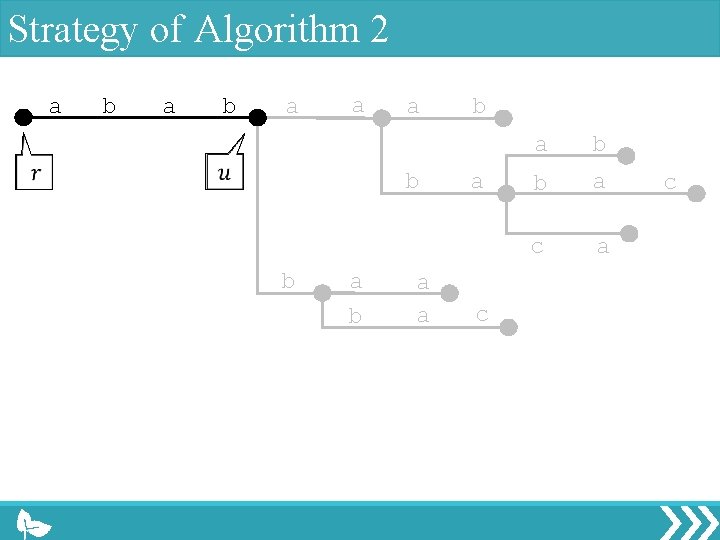
Strategy of Algorithm 2 a b a a a b b a b a a c a b b a c

Strategy of Algorithm 2 a b a a a b b b a a b a a c a b b a c

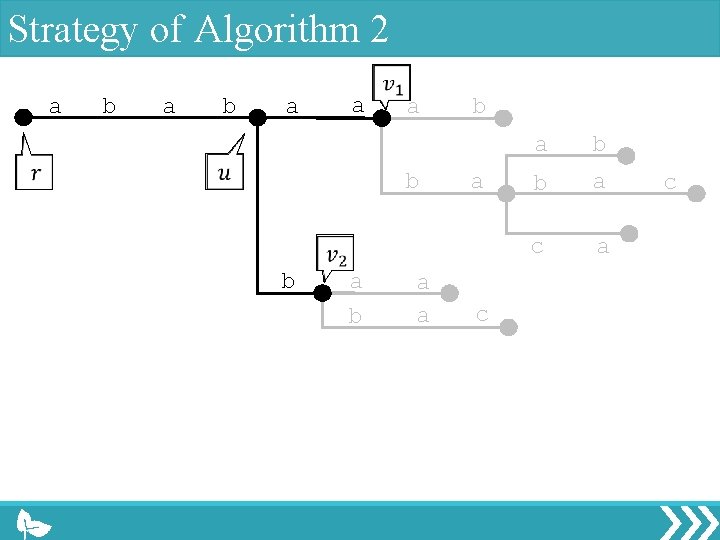
Strategy of Algorithm 2 a b a a a b b a b a a c a b b a c

Strategy of Algorithm 2 a b a a a b b a c c

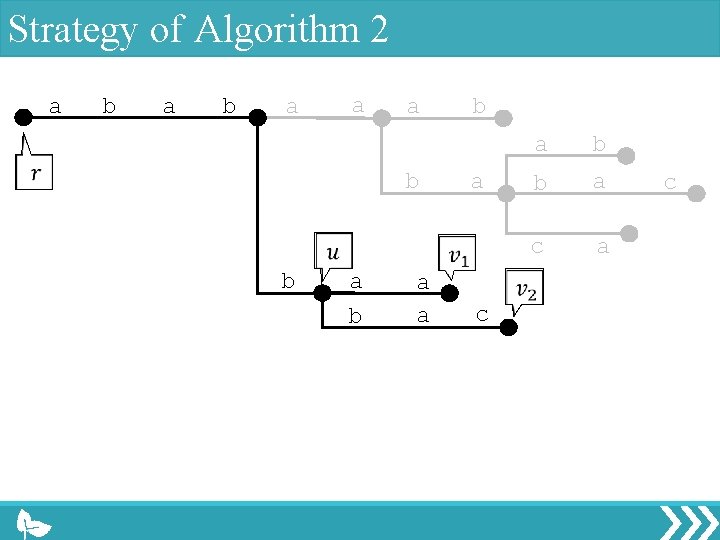
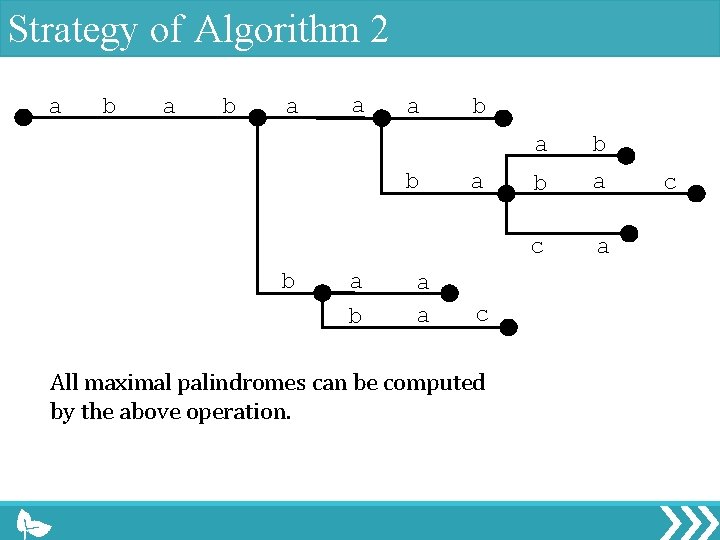
Strategy of Algorithm 2 a b a a a b b a a b a c a b b a c

Strategy of Algorithm 2 a b a a a b b a a b a c All maximal palindromes can be computed by the above operation. a b b a c