Prsentation du cours Thorie Bases de la thorie

Présentation du cours Théorie Bases de la théorie des sous-ensembles flous Pratique Utiliser la théorie (exercices) Applications Fis. Pro Maria Rifqi-Berger 1

Bibliographie « La logique floue » , B. Bouchon-Meunier, Quesais-je? PUF, N° 2702. « Logique floue – exercices corrigés et exemples d'applications » , B. Bouchon-Meunier, L. Foulloy et M. Ramdani, Cépaduès éd. , 1998. « La logique floue et ses applications » , B. Bouchon-Meunier, Addison Wesley éd. , 1995 « Fuzzy sets, uncertainty and information » , G. Klir and T. Folger, Prentice Hall ed. , 1988. Maria Rifqi-Berger 2

Plan du cours Introduction Présentation du cours Définitions de base Sous-ensemble flou (sef) Caractéristiques de sef Opérations sur les sefs Quelques applications commerciales de la logique floue Maria Rifqi-Berger 3

Introduction L'imprécision du monde réel Théorie des sous-ensembles flous Le flou est partout Le flou est humain Le flou est plus souple « mesurer une gradation dans l'appartenance à un ensemble » Une théorie mathématique formelle pour la prise en compte de l'imprécision et des incertitudes Article fondateur: « Fuzzy Sets » , L. A. Zadeh, in Information and Control, 1965. Maria Rifqi-Berger 4

Historique 1965 : Théorie des ensembles flou introduite par L. A. Zadeh (UC Berkeley) En 1973, le Pr. Zadeh publie un article (dans l'IEEE Transactions on Systems, Man and Cybernetics) qui mentionne pour la première fois le terme de variables linguistiques (dont la valeur est un mot et non un nombre). En 1974, Mamdani (Université de Londres) réalise un contrôleur flou expérimental sur un moteur à vapeur. En 1980, F. L. Smidth & Co. A/S (au Danemark) met en application la théorie de la logique floue dans le contrôle de fours à ciment. C'est la première mise en oeuvre pratique de cette nouvelle théorie. Dans les années 80, plusieurs applications commencent à immerger (notamment au Japon). En 1987, « explosion du flou » au Japon (avec le contrôle du métro de Sendaï) et qui atteint son apogée en 1990 (fuzzymania). Aujourd'hui, une vaste gamme de nouveaux produits ont une étiquette « produit flou » (Fuzzy). Maria Rifqi-Berger 5

Gestion des imprécisions Approche conventionnelle Dissoudre le flou puis traiter des données précises informations floues informations précises part importante d'arbitraire analyse de la sensibilité indispensable plusieurs jeux de données traités un par un comparaison des résultats Maria Rifqi-Berger 6

Gestion des imprécisions Approche floue Traiter des données floues puis dissoudre le flou Garder le flou comme une information Reporter la dissolution du flou le plus tard possible et sur la décision uniquement Accroissement de la fiabilité et de la stabilité du système Maria Rifqi-Berger 7

Gestion des imprécisions Théorie des ensembles flous introduite par Lotfi Zadeh en 1965. Modèle mathématique pour représenter l'imprécision et l'incertitude. Idée des ensembles flous facile à comprendre : Freine dans 32 m 50 ou Freine bientôt La précision n'est pas toujours utile. Capable d'interpréter des informations imprécises et d'agir. Maria Rifqi-Berger 8

Ensembles classiques / Ensembles flous ensemble classique = ensemble des objets satisfaisant des propriétés précises ensemble flou = ensemble des objets satisfaisant des propriétés imprécises Exemple : ensemble des nombres compris entre 6 et 8 fonction caractéristique : m : R {0, 1} m(x) = 1 si 6 x 8 0 sinon. Exemple : ensemble des nombres proches de 7 fonction d'appartenance : : X [0, 1] (x) pas unique. différence majeure : unicité fonction caractéristique / infinité fonction d'appartenance Maria Rifqi-Berger 9

Théorie des sous-ensembles flous X ensemble de référence A sous-ensemble flou de X défini par une fonction d'appartenance X [0, 1] Caractéristiques Noyau : éléments appartenant de façon absolue Noy(A) = {x X / (x) = 1} Support : éléments appartenant au moins un peu Supp(A) = {x X / (x) 0} Maria Rifqi-Berger 10

Théorie des sous-ensembles flous Infinité de fonctions d'appartenance possibles flexibilité, ajustement maximal pour une situation donnée Ensemble flou = toujours et seulement des fonctions Toute fonction X [0, 1] est un ensemble flou dans le sens mathématique. D'un point de vue sémantique, il faut qu'une telle fonction soit interprétable à l'aide de propriétés imprécises décrivant les éléments de X. Maria Rifqi-Berger 11

Probabilité / Flou ensembles flous = déguisement pour les statistiques ? NON A B p(B) = 0. 9 Quelle bouteille boirez-vous ? Maria Rifqi-Berger 12

Probabilité / Flou A contient par exemple de l'eau vaseuse, pas de l'acide chlorydrique. A est proche d'un liquide tout à fait potable. Sur 100 bouteilles B, 90 sont potables, 10 sont dégoûtantes voire fatales. Il vaut mieux boire de l'eau vaseuse que de prendre le risque de mourir. 2 Maria Rifqi-Berger philosophies différentes 13

La théorie des sous-ensembles flous Une extension de la théorie des ensembles classiques Une théorie plus générale qui englobe la théorie des ensembles classiques La logique floue : application de la théorie des sousensembles flous pour la modélisation du raisonnement La théorie des ensembles classiques est un cas particulier Des choix sont à faire pour conserver certaines des propriétés existantes dans la théorie des ensembles classiques Toutes les propriétés ne peuvent pas être conservées en même temps Extension de la logique classique La commande floue : utilisation de la logique floue pour le contrôle de systèmes automatiques Cas particulier de la logique floue Maria Rifqi-Berger 14

Exemples de sous-ensembles flous X={moto, auto, train} (moyens de transport) A: sous-ensemble de X des moyens de transport rapides A= 0. 7 / moto + 0, 5 / auto + 1. 0 / train X=[0, 130] (ensemble des âges) A: sous-ensemble de X des âges jeunes Jeune 1 0 Maria Rifqi-Berger 15 20 30 35 X 15
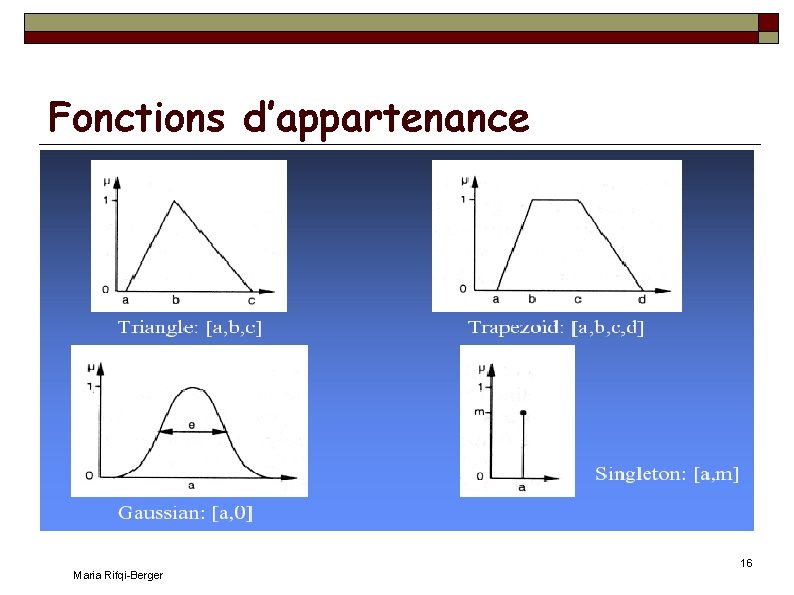
Fonctions d’appartenance Maria Rifqi-Berger 16

Caractéristiques d'un sef Soit X un univers, et A un sous-ensemble flou de fonction d'appartenance f. A. Noyau de A : Support de A : Supp(A) = {x X | f. A(x)>0} Hauteur de A : Noy(A) = {x X | f. A(x)=1} h(A) = supx X f. A(x) Cardinalité de A: |A| = x X f. A(x) Maria Rifqi-Berger 17
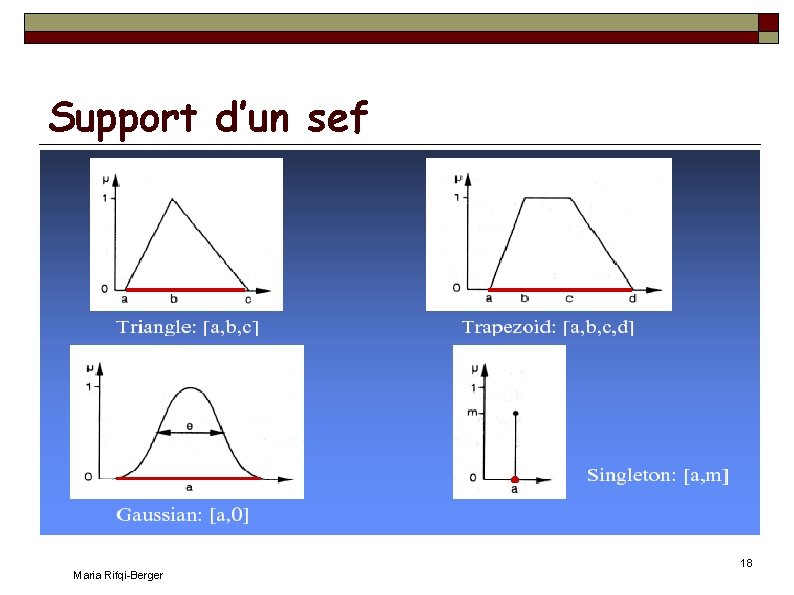
Support d’un sef Maria Rifqi-Berger 18
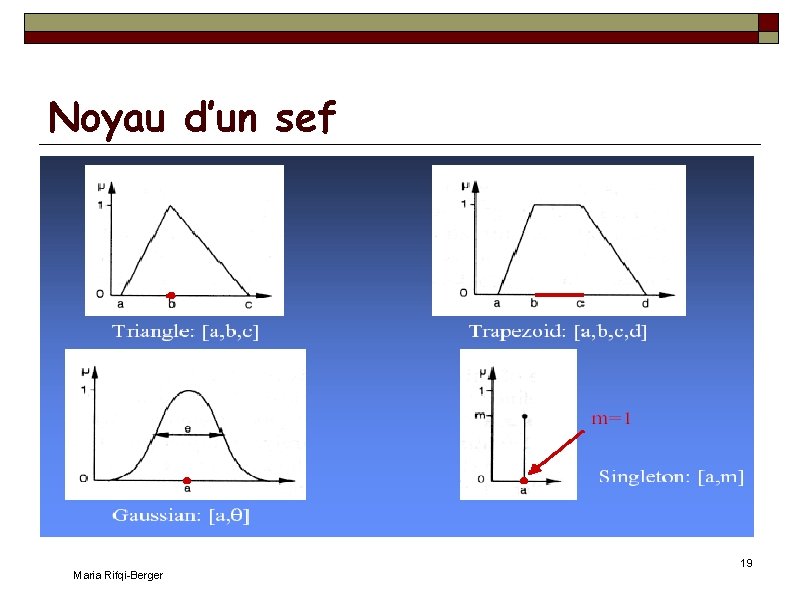
Noyau d’un sef Maria Rifqi-Berger 19

Opérations sur les sefs (1) Extension des opérations de la théorie des ensembles classiques: =, , complément Soient A et B deux sefs de X, de f. d'a. f. A et f. B. Égalité de sefs: Inclusion de sefs: A B ssi x X, f. A (x) < f. B(x) Intersection de sefs: A B: A = B ssi x X, f. A (x) = f. B(x) x X, f. A∩ B (x) = min(f. A (x), f. B(x)) Union de sefs: A B: x X, f. A B (x) = max(f. A (x), f. B(x)) Maria Rifqi-Berger 20

Opérations sur les sefs (2) Certaines propriétés de la théorie des ensembles classiques sont vérifiées (à faire en exercice): A U∅ = A, A ∩ ∅ = ∅, A U X = X, A ∩ X = A Associativité de ∩ et de U : Commutativité de ∩ et de U : (A U B) U C = A U(B U C) A∩B = B∩A Distributivité de ∩ par rapport à U : A∩(B U C) = (A∩B) U(A∩C) A U(B∩C) = (A U B)∩(A U C) Maria Rifqi-Berger 21

Opérations sur les sefs (3) Complément Ac d'un sous-ensemble flou Certaines propriétés de la théorie des ensembles classiques sont vérifiées (à faire en exercice): x X, f. Ac (x) = 1 – f. A(x) (Ac)c = A (A∩B)c = Ac U Bc (A U B)c = Ac ∩ Bc D'autres propriétés ne le sont pas (généralement): Ac ∩A ≠∅ (contradiction) Ac U A ≠ X (tiers exclu). Maria Rifqi-Berger 22

Opérations sur les sefs (4) Autres extensions des opérations de la théorie des ensembles classiques: ∩ et U Ces opérations sont en fait des fonctions mathématiques F: [0, 1]×[0, 1] telle que x, y, F(x, y) [0, 1]. L'intersection peut être réalisée en prenant comme opérateur une t-norme (opérateur ET) L'union peut être réalisée en prenant comme opérateur une t-conorme (opérateur OU) Maria Rifqi-Berger 23

Opérations sur les sefs (5) Justification des choix des opérateurs Les opérateurs min et max sont les seuls opérateurs qui soient commutatifs, associatifs, mutuellement distributifs, continus et doublement non décroissants D'autres opérateurs sont possibles : conjonction normes triangulaires (t-normes) disjonction conormes triangulaires (t-conormes) Propriétés communes : associativité, commutativité, monotonie, élément neutre. Maria Rifqi-Berger 24
![Normes triangulaires (t-normes) Soit une fonction ⊤: [0, 1]×[0, 1] telle que x, y, Normes triangulaires (t-normes) Soit une fonction ⊤: [0, 1]×[0, 1] telle que x, y,](http://slidetodoc.com/presentation_image/5b9376b00a88c30f90c76d572ac29650/image-25.jpg)
Normes triangulaires (t-normes) Soit une fonction ⊤: [0, 1]×[0, 1] telle que x, y, z [0, 1]: Exemples de telles fonctions : ⊤(x, y) = ⊤(y, x) (commutativité) ⊤(x, ⊤(y, z)) = ⊤( ⊤(x, y), z) (associativité) ⊤(x, y) ⊤(z, t) si x z et y t (monotonie) ⊤(x, 1) = x (1 est élément neutre) min(x, y), x⋅y, max(x+y-1, 0) ⊤ est une t-norme Utilisée pour l'intersection ou la conjonction Maria Rifqi-Berger 25
![Normes triangulaires (t-conormes) Soit une fonction : [0, 1]×[0, 1] telle que x, y, Normes triangulaires (t-conormes) Soit une fonction : [0, 1]×[0, 1] telle que x, y,](http://slidetodoc.com/presentation_image/5b9376b00a88c30f90c76d572ac29650/image-26.jpg)
Normes triangulaires (t-conormes) Soit une fonction : [0, 1]×[0, 1] telle que x, y, z [0, 1]: Exemples de telle fonction: (x, y) = (y, x) (commutativité) (x, (y, z)) = ( (x, y), z) (associativité) (x, y) (z, t) si x z et y t (monotonie) (x, 0) = x (0 est élément neutre) max(x, y), x+y-x⋅y, min(x+y, 1) est une t-conorme Utilisée pour l'union Maria Rifqi-Berger 26

Dualité t-norme / t-conorme Le choix d'une t-norme et celui d'une t-conorme est lié Etant donné un opérateur de complémentation Déf. : Une t-norme et une t-conorme sont duales si et seulement si : 1 – ⊤(x, y) = (1 -x, 1 -y) 1 – (x, y) = ⊤(1 -x, 1 -y) En termes de sous-ensembles, la dualité permet de conserver les lois de De Morgan Ainsi, par exemple, le min et le max sont duaux : par exemple: fc = 1 -f on a : 1 – min(x, y) = max(1 -x, 1 -y) ainsi que 1 – max(x, y) = min(1 -x, 1 -y) On montre que (à faire en exercice) les opérateurs probabilistes sont duaux les opérateurs de Lukasiewicz sont duaux Maria Rifqi-Berger 27
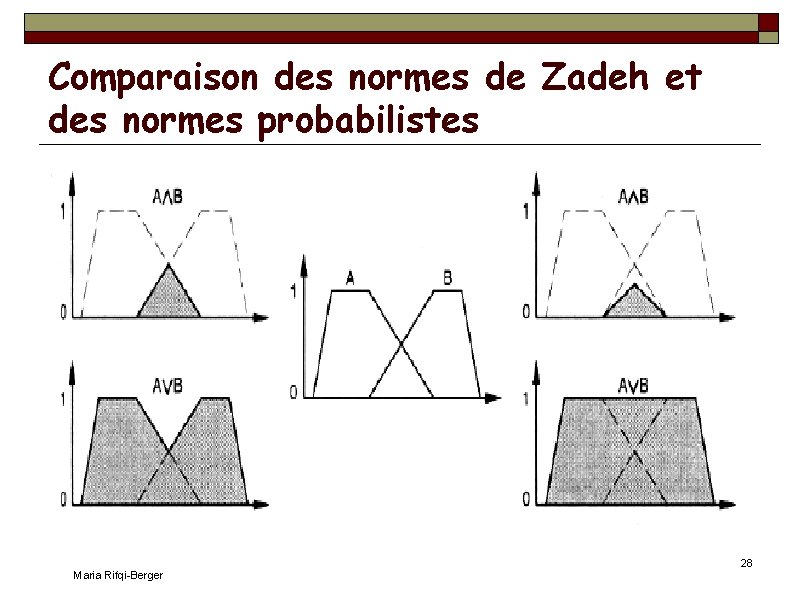
Comparaison des normes de Zadeh et des normes probabilistes Maria Rifqi-Berger 28

Exemples X={moto, auto, train} (moyens de transport) Transport rapide: A= 0. 7 / moto + 0, 5 / auto + 1. 0 / train Transport familial: B= 0. 1 / moto + 1. 0 / auto + 0. 6 / train X=[0, 130] (ensemble des âges) Jeune 1 0 Maria Rifqi-Berger 15 20 Salarié 30 35 55 70 X 29

Caractéristiques d'un sef (2): -coupes Une -coupe (alpha-coupe) d'un sef A est un sous-ensemble classique A extrait du sef A, défini en fonction d'un seuil [0, 1] fixé : soit [0, 1], x X, x A si et seulement si f. A(x) A est un sous-ensemble classique de X. (f. A prend ses valeurs dans {0, 1}). On vérifie que (à faire en exercice): Si > ' alors A A ' et si B A alors B A (A ∩ B) = A ∩ B , et (A B) = A B x X, f. A(x) = sup ]0, 1] f (x) (i. e. on peut reconstruire A à partir de ses -coupes). Maria Rifqi-Berger 30
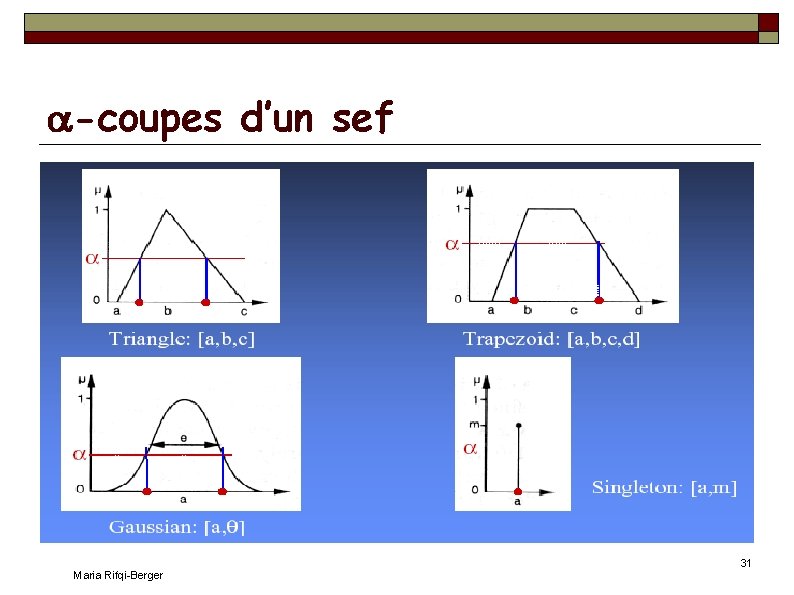
-coupes d’un sef Maria Rifqi-Berger 31

Relations entre sous-ensembles flous Relation: notion fondamentale des mathématiques classiques Les relations établissent des liens entre éléments Basée sur le produit cartésien d'ensembles soit d'un même ensemble soit d'ensembles différents Elles permettent de construire des applications une application est une relation particulière Maria Rifqi-Berger 32

Produit cartésien de sefs Cas où l'on désire combiner l'information venant de plusieurs ensembles de référence Soit X 1 et X 2, deux univers de référence et X leur produit cartésien (classique), X=X 1×X 2, dont les éléments sont les couples (x 1, x 2), x 1 X 1 et x 2 X 2 Déf. : Soient A 1 et A 2 respectivement définis sur X 1 et X 2, on définit le produit cartésien A=A 1×A 2 comme un sef de X, de fonction d'appartenance: x X, x=(x 1, x 2), f. A(x)=min( f. A 1(x 1), f. A 2(x 2) ) Maria Rifqi-Berger 33
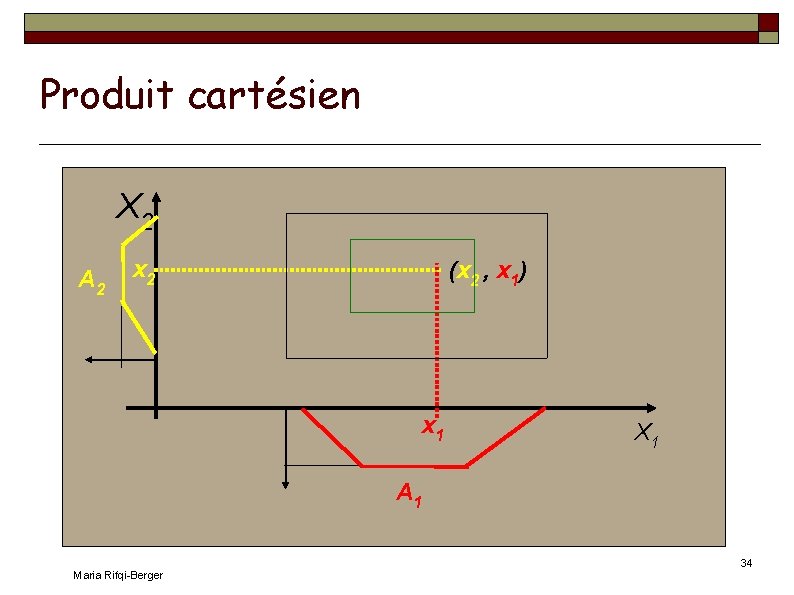
Produit cartésien X 2 A 2 x 2 (x 2 , x 1) x 1 X 1 A 1 Maria Rifqi-Berger 34

Exemple d'application du produit cartésien X 1={moto, auto, train} (moyens de transport) Transport rapide: A 1= 0. 7 / moto + 0, 5 / auto + 1. 0 / train X 2={pas. Cher, cher} (prix) Prix souhaité : A 2= 0. 7 / pas. Cher + 0. 4 / cher Donnez la fonction d'appartenance du produit cartésien (transport rapide, prix souhaité) Maria Rifqi-Berger 35

Relations floues Une relation floue R entre 2 ensembles de références X et Y, est un sous-ensemble flou de Xx. Y de fonction d'appartenance f. R Si X et Y sont finis, R peut être représentée par la matrice M(R) des valeurs de sa fonction d'appartenance Exemple: la relation « est préféré à » sur Xx. X avec X={Train, Voiture, Moto, Avion} La composition de 2 relations floues R 1 sur Xx. Y et R 2 sur Yx. Z définit une relation floue R=R 1˚ R 2 sur Xx. Z de f. a. définie par : (x, z) Xx. Z, f. R(x, z)= sup y Y min(f. R 1(x, y), f. R 2(y, z)) Maria Rifqi-Berger 36

Relation floue transitive Transitivité : propriété très utilisée pour des relations si A ressemble à B, et que B ressemble à C, alors est-ce que A ressemble à C ? si x < y et que y < z alors x < z Une relation floue R sur X est dite transitive si elle vérifie R R R. En particulier, si on utilise la composition maxmin, on dira que la relation floue R est max-min transitive si : (x, z) Xx. Z, f. R(x, z) sup y Y min(f. R(x, y), f. R(y, z)) Maria Rifqi-Berger 37
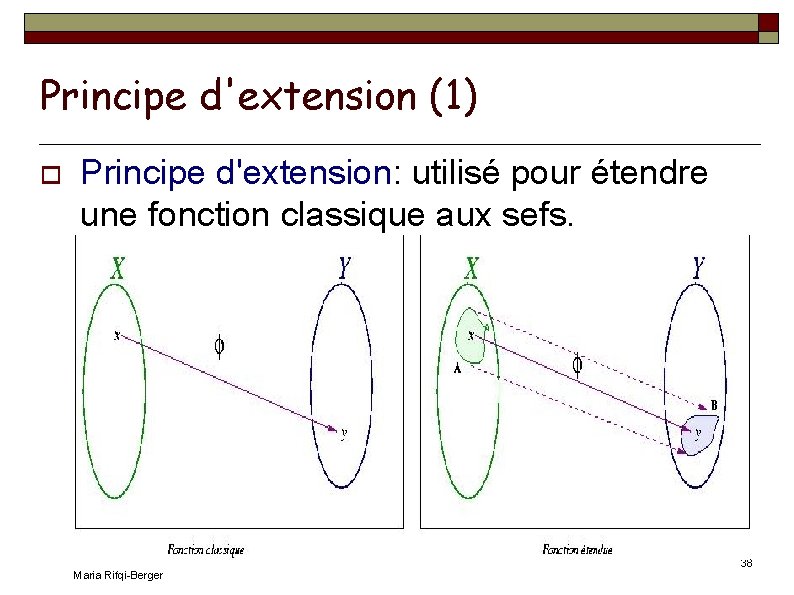
Principe d'extension (1) Principe d'extension: utilisé pour étendre une fonction classique aux sefs. Maria Rifqi-Berger 38
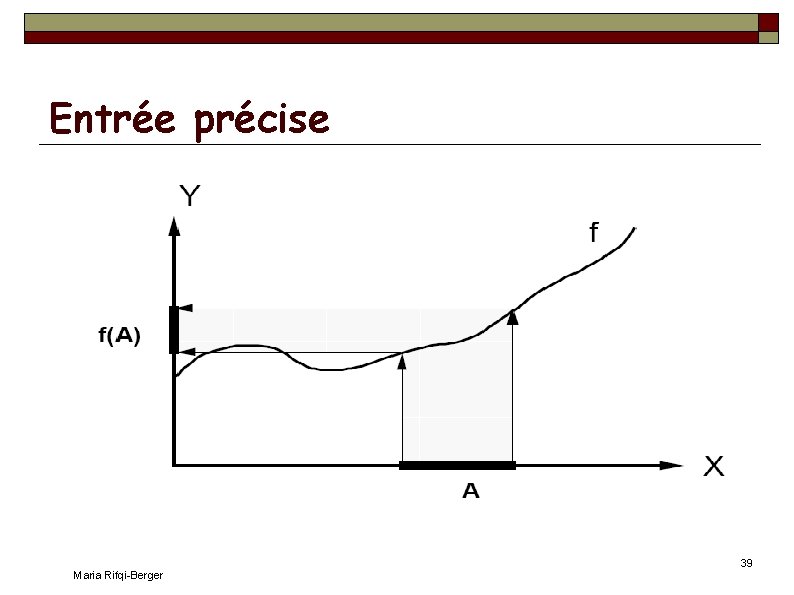
Entrée précise Maria Rifqi-Berger 39
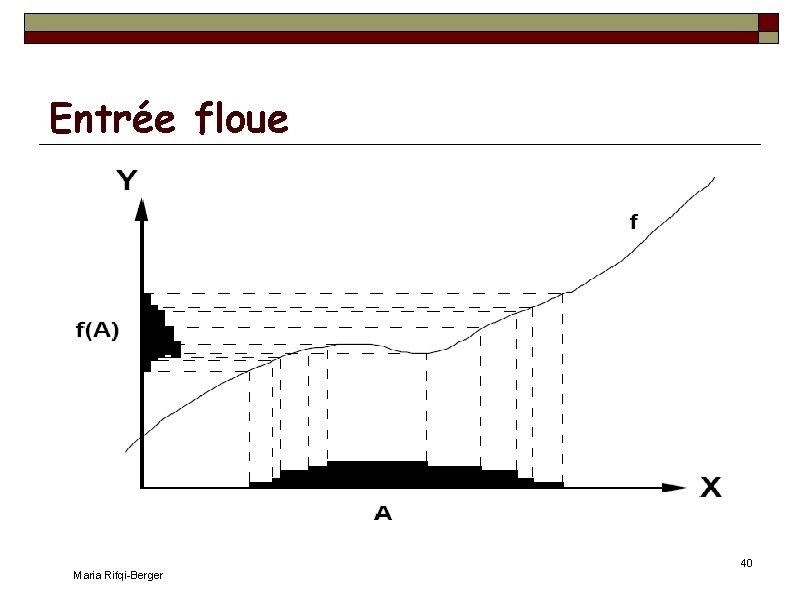
Entrée floue Maria Rifqi-Berger 40

Principe d'extension (2) Idée: possédant une fonction sur un univers classique X, permettre son utilisation avec des sefs de X. Définition: Étant donné un sef A de X, et une application de X vers Y, le principe d'extension permet de définir un sef B de Y associé à A par : y Y, f. B(y)= sup{x X | y= (x)}f. A(x) si -1(y)≠∅ 0 sinon Le sef B est l'image du sef A par la fonction . Maria Rifqi-Berger 41

Exemple d'application du principe d'extension (1) X={camion, caravane, voiture, moto} (moyens de transport) Y={Rapide, Lente, Normale} (mesures des vitesses) On définit la fonction qui associe une vitesse à un moyen de transport : (camion)=L, (caravane)=L, (voiture)=N, (moto)=R Nouveau véhicule: side-car= 0. 5|moto + 0. 4|voiture + 0. 1|caravane Mesure de la vitesse d'un side-car? f. B(L)= max(fsc(camion), fsc(caravane))=max(0, 0. 1)= 0. 1 f. B(N)= fsc(voiture)= 0. 4 f. B(R)= fsc(moto)= 0. 5 Maria Rifqi-Berger 42

Exemples d'application du principe d'extension (2) Fonction mathématique classique : (x)= x 2 A un sef de [0, 1] de f. a. f. A, le sef B de [0, 1[ de f. a. f. B qui correspond à la A 2. y Y, f. B(y)= sup{x X | y=x 2} f. A(x) si -1(y)≠∅ 0 sinon Mesure de surprise : (p)= -log(p) A un sef de [0, 1] de f. a. f. A, le sef B de [0, 1[ de f. a. f. B qui correspond à la valeur floue de surprise causée par A. Maria Rifqi-Berger 43
- Slides: 43