Proxy signature schemes based on factoring Source Information

Proxy signature schemes based on factoring Source: Information Processing Letters, Vol. 85, 2003, pp. 137– 143 Author: Zuhua Shao Advisor: Dr. Chang, Chin-Chen Reporter: Wang, Shing-Shoung Date : 2004/12/21 1

Outline Introduction n The proxy-unprotected signature scheme n The proxy-protected signature scheme n Security Analysis n Conclusions n 2

Introduction Proxy signature scheme: 1. Full delegation. 2. Partial delegation. 3. Delegation by warrant. n Proxy signature schemes based on factoring: 1. Proxy-unprotected scheme. 2. Proxy-protected scheme. n 3

The proxy-unprotected signature scheme(1/5) n Notations: p&q are large primes n=pq. e&d satisfying the properties e*d = 1 (mod φ(n)) where d is large and φ(n) is the Euler–Totient function. h(. ): One-way hash function 4

The proxy-unprotected signature scheme(2/5) n Proxy generation: p 0 mw||SNi Proxy users pi hashing EK 0 ( )=vi. (vi, mw, SNi) vi=h(mw, SNi)-d 0(mod n 0) original signer p 0 Public key, PK 0(n 0, e 0) Private key, K 0(p 0, q 0, d 0) Secure manner verify equation: vie 0 h(mw, SNi)=1(mod n 0) 5

The proxy-unprotected signature scheme(3/5) n Proxy-unprotected mono-signature : pi r=te 0(mod n 0) t [1, n 0] || Message: m hashing k y=tvik(mod n 0) The proxy signature of the message m is(m, mw, SNi, y, k) The verifier computes r’=ye 0 h(mw, SNi)k(mod n 0) ? h(m, r’)=h(m, r)=k Because vie 0=h(mw, SNi)-1(mod n 0) r’=te 0 vike 0 h(mw, SNi)k=te 0=r (mod n 0) 6

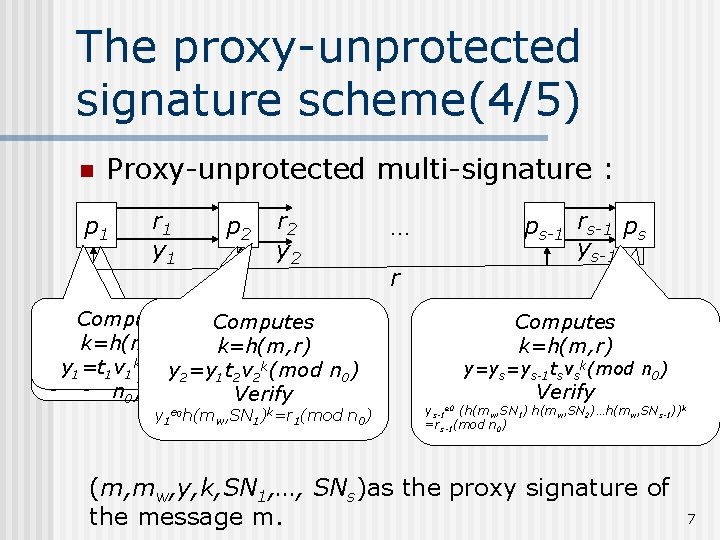
The proxy-unprotected signature scheme(4/5) n Proxy-unprotected multi-signature : p 1 r 1 y 1 p 2 r 2 y 2 Computes randomly chooses k=h(m, r) t 1 [1, n 0], computes t [1, n 2 0], computes k(mod n ) y 1=t v y =y t v 1 1 e e 0 0 2 1 2 2 0 r 1=t 1 (modr 2 n=r 0) 1 t 2 (mod n 0) Verify y 1 e 0 h(mw, SN 1)k=r 1(mod n 0) … r ps-1 rs-1 ps ys-1 Computes randomly chooses k=h(m, r) ts [1, n 0], computes k y=ys=ys-1 ts v s (mod n 0) e 0 r=rs=rs-1 ts (mod n 0) Verify ys-1 e 0 (h(mw, SN 1) h(mw, SN 2)…h(mw, SNs-1))k =rs-1(mod n 0) (m, mw, y, k, SN 1, …, SNs)as the proxy signature of the message m. 7

The proxy-unprotected signature scheme(5/5) n n n Proxy-unprotected multi-signature : Each verifier can verify the proxy signature by checking the following equations: r’=ye 0(h(mw, SN 1)h(mw, SN 2)…h(mw, SNs))k(mod n 0) and checks h(m, r’)=k If pi found that the data is invalid, p 1 p 2 the error comes from … pi-1 pi pi+1 … ps otherwise the error comes from. 8

The proxy-protected signature scheme(1/4) n Proxy generation: p 0 mw||IDi ui=[vi/ni] and ωi=viei(mod n i) hashing EK 0 ( Proxy users pi )=vi. (ωi, mw, ui) vi=h(mw, IDi)-d 0(mod n 0) original signer p 0 Public key, PK 0(n 0, e 0) Private key, K 0(p 0, q 0, d 0) Secure manner each proxy user pi Public key, PKi(ni, ei) Private key, Ki(pi, qi, di) recovers the key vi=ui×ni+(ωidi mod ni) verify equation: vie 0 h(mw, IDi)=1(mod n 0) 9

The proxy-protected signature scheme(2/4) n Proxy-protected mono-signature : pi r=te 0(mod n 0) t [1, n 0] u= kdi(mod ni) y=tvik(mod ni) || Message: m hashing k The proxy signature of the message m is(m, mw, y, u, IDi) The verifier computes k’=uei(mod ni) r’=ye 0 h(mw, IDi)k’(mod n 0) ? h(m, r’)=h(m, r)=k=k’ Because vie 0=h(mw, IDi)-1(mod n 0) k’=uei=kd 1 ei(mod ni)=k r’=te 0 vike 0 h(mw, IDi)k=te 0=r (mod n 0) 10

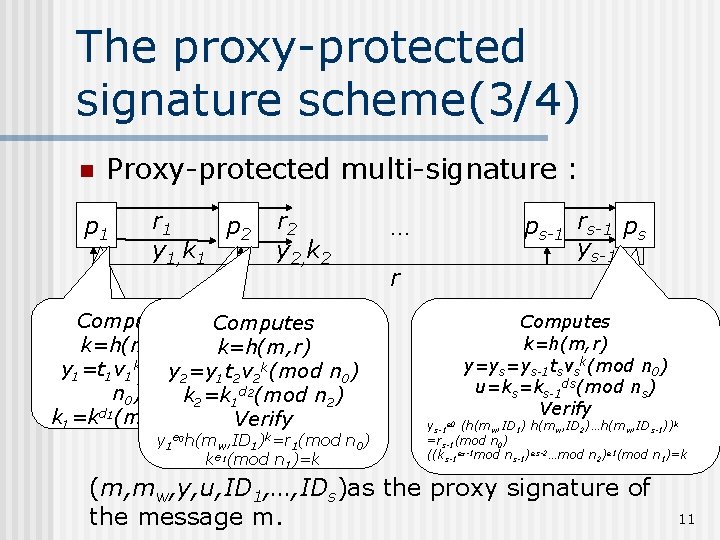
The proxy-protected signature scheme(3/4) n Proxy-protected multi-signature : p 1 r 1 p 2 y 1, k 1 r 2 y 2, k 2 Computes randomly chooses k=h(m, r) t 1 [1, n t [1, n 0], computes 2 0], computes k y 1=t v 1 (mod y=r =y v 2 k(mod e 01(mod 2) 1 et 02(mod r 1=t r n t n 0) 1 2 0 1 2 d n 0) k 2=k 1 2(mod n 2) k 1=kd 1(mod n 1) Verify y 1 e 0 h(mw, ID 1)k=r 1(mod n 0) ke 1(mod n 1)=k ps-1 rs-1 ps ys-1 … r Computes randomly chooses k=h(m, r) ty=y k(mod n ) s [1, n 0], computes =y s s-1 tsv s e 0(mod n 0) r=r =r t ds s s-1 s u=k =k (mod n )0 s s-1 Verify s ys-1 (h(mw, ID 1) h(mw, ID 2)…h(mw, IDs-1))k =rs-1(mod n 0) ((ks-1 es-1 mod ns-1)es-2…mod n 2)e 1(mod n 1)=k e 0 (m, mw, y, u, ID 1, …, IDs)as the proxy signature of the message m. 11

The proxy-protected signature scheme(4/4) n n n Proxy-protected multi-signature : Each verifier can verify the proxy signature by checking the following equations: r’=ye (h(mw, ID 1)h(mw, ID 2)…h(mw, IDs))k 0 (mod n 0) and checks h(m, r’)=k If pi found that the data is invalid, p 1 p 2 the error comes from … pi-1 pi pi+1 … ps otherwise the error comes form. 12

Security Analysis n In the proposed proxy-unprotected signature scheme, the original signer plays the role of the Trusted Authority, TA. n In the proposed proxy-protected signature scheme, any attacker, including the original signer, is not able to compute the partial signature u from k. 13

Conclusions n n The proposed proxy-protected signature scheme needs some more computation, communication and storage, any outsider can identify the actual signers who indeed proxy sign the message. This property avoids possible disputes who should be responsible for the proxy signature besides the original signer. The proposed proxy-protected signature scheme protects the privacy of proxy signers which is anonymous by use of anonymous public key certificates. 14