Proximity Planar triangulations Problem definitions 1 TRIANGULATION INSTANCE

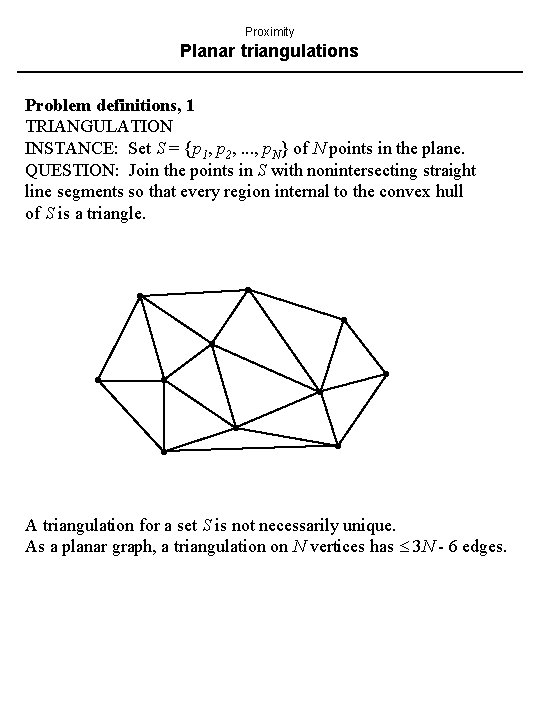
Proximity Planar triangulations Problem definitions, 1 TRIANGULATION INSTANCE: Set S = {p 1, p 2, . . . , p. N} of N points in the plane. QUESTION: Join the points in S with nonintersecting straight line segments so that every region internal to the convex hull of S is a triangle. A triangulation for a set S is not necessarily unique. As a planar graph, a triangulation on N vertices has 3 N - 6 edges.

Proximity Planar triangulations Problem definitions, 2 CONSTRAINED TRIANGULATION INSTANCE: Set S = {p 1, p 2, . . . , p. N} of N points in the plane, and set E = { {pi, pj}, … } of nonintersecting edges on S. QUESTION: Join the points in S with nonintersecting straight line segments so that every region internal to the convex hull of S is a triangle and every edge of E is in the triangulation.

Proximity Planar triangulations Problem definitions, 3 POLYGON TRIANGULATION INSTANCE: Polygon P = {p 1, p 2, . . . , p. N} of N points in the plane. QUESTION: Triangulate the interior of P. As a polygon, P has a set of edges by definition, hence POLYGON TRIANGULATION is a special case of CONSTRAINED TRIANGULATION. We encountered this problem in: 1. Kirkpatrick’s triangle refinement method for point location 2. Hertel’s convex polyhedra intersection algorithm

Proximity Planar triangulations Optimizations Beyond simply triangulating a set S, some problems involve optimizations of the triangulation. For example: 1. Minimize total length of triangulation edges 2. Minimize difference among internal angles (i. e. , “triangles that are more or less equilateral”) A For example, A and B are both valid triangulations, but B is preferred to A under both optimization criteria. Complexity Time complexity depends on the problem and optimization. A

Proximity Planar triangulations Greedy triangulation A “greedy” algorithm chooses the optimum choice available at each step of an algorithm and never undoes anything done earlier. Suppose the problem is TRIANGULATION, with the desired optimization of minimizing the total edge length. We will examine some greedy algorithms for this problem. If the objective is to minimize total edge length, the greedy approach is to add at each stage the shortest possible edge that does not intersect any existing edge.

Proximity Planar triangulations Simple greedy algorithm 1 Generate all ( N 2) O(N 2) possible edges. store in P. /* O(N 2) */ 2 Sort P on increasing edge length. /* O(N 2 log N 2) */ 3 Initialize triangulation T to . 4 while P /* O(N 2) */ 5 e = shortest (first) edge in P 6 P = P - {e} 7 keep = TRUE 8 for every edge t T /* O(N), by Euler’s formula */ 9 if e t 10 keep = FALSE 11 endif 12 endfor 13 if keep = TRUE 14 T = T {e} 15 endif 16 endwhile Analysis O(N 2) O(N 3) (An aside: Preparata says sorting requires O(N 2 log N) time, rather than O(N 2 log N 2). )