Prove Triangles Congruent by SSS Prove Triangles Congruent

Prove Triangles Congruent by SSS

Prove Triangles Congruent by SSS • Side-Side (SSS) Congruence Postulate:

Prove Triangles Congruent by SSS • Side-Side (SSS) Congruence Postulate: – If three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent.

Prove Triangles Congruent by SSS • Side-Side (SSS) Congruence Postulate: – If three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent. – In other words:

Prove Triangles Congruent by SSS • Side-Side (SSS) Congruence Postulate: – If three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent. – In other words: • If all the sides are the same, the triangles are the same.

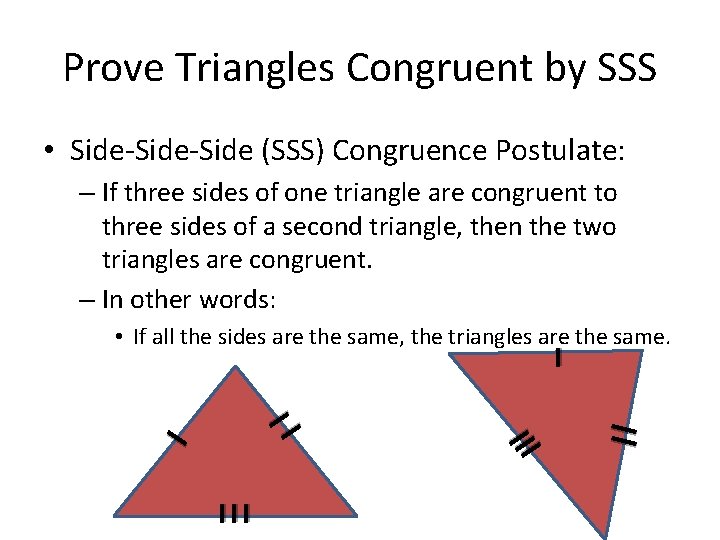
Prove Triangles Congruent by SSS • Side-Side (SSS) Congruence Postulate: – If three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent. – In other words: • If all the sides are the same, the triangles are the same.

Prove Triangles Congruent by SSS • Given: • KL = NL, KM = NM L K N M • Prove KLM = NLM

Prove Triangles Congruent by SSS 8 4 6 8 8 6

Prove Triangles Congruent by SSS • Show you know LMA = LOA M L A O

Prove Triangles Congruent by SSS • Using the distance formula:

Prove Triangles Congruent by SSS • Using the distance formula: – With a set of points use the distance formula to find the length between two points.

Prove Triangles Congruent by SSS • Using the distance formula: – With a set of points use the distance formula to find the length between two points. – JKL has vertices J (-3, -2) K (0, -2) L (-3, -8) – RST has vertices R (10, 0) S (10, -3) T (4, 0)

Prove Triangles Congruent by SSS • Using the distance formula: – With a set of points use the distance formula to find the length between two points. – JKL has vertices J (-3, -2) K (0, -2) L (-3, -8) – RST has vertices R (10, 0) S (10, -3) T (4, 0) – Find out if the triangles are congruent.

Prove Triangles Congruent by SSS • Using the distance formula: – With a set of points use the distance formula to find the length between two points. – JKL has vertices J (-3, -2) K (0, -2) L (-3, -8) – RST has vertices R (10, 0) S (10, -3) T (4, 0) – Find out if the triangles are congruent.

Prove Triangles Congruent by SSS • How to construct a congruent triangle.