Prove Similar Triangles Skill 38 Objective HSGSRT 5GPE

Prove Similar Triangles Skill 38

Objective HSG-SRT. 5/GPE. 5: Students are responsible for using AA Postulate and SAS and SSS Theorems, also similarity to find indirect measurements.

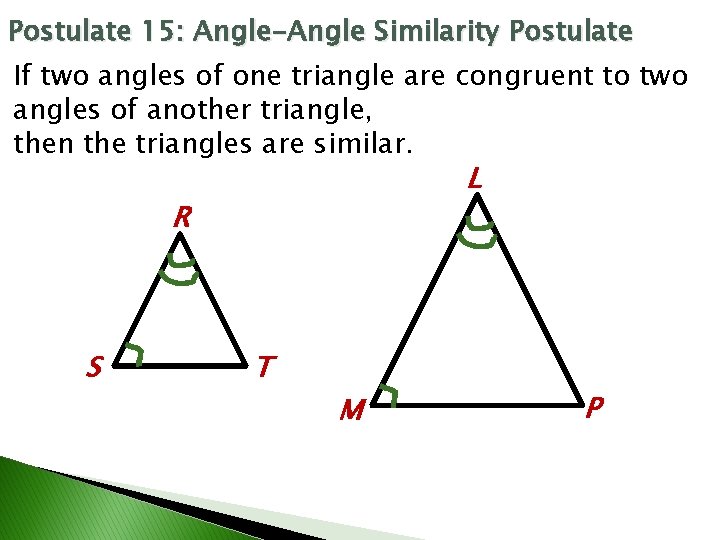
Postulate 15: Angle-Angle Similarity Postulate If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. L R S T M P

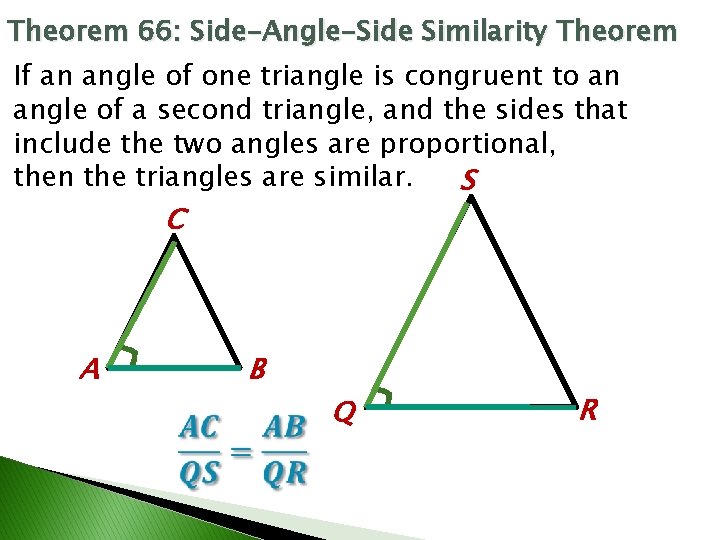
Theorem 66: Side-Angle-Side Similarity Theorem If an angle of one triangle is congruent to an angle of a second triangle, and the sides that include the two angles are proportional, then the triangles are similar. S C A B Q R

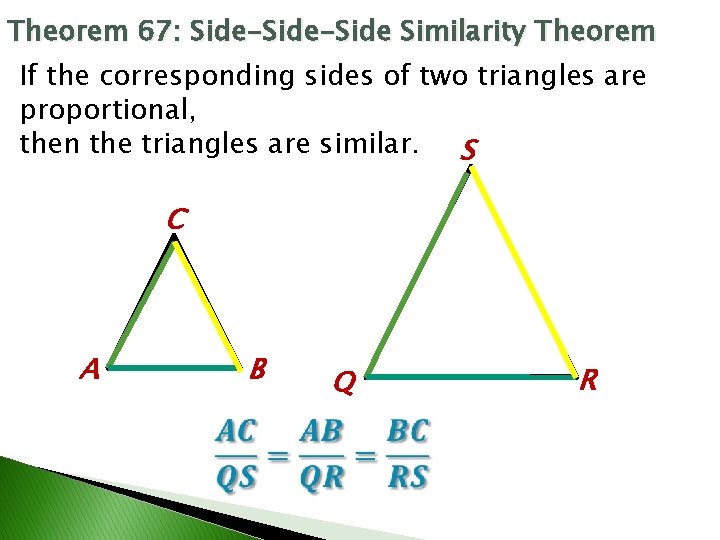
Theorem 67: Side-Side Similarity Theorem If the corresponding sides of two triangles are proportional, then the triangles are similar. S C A B Q R

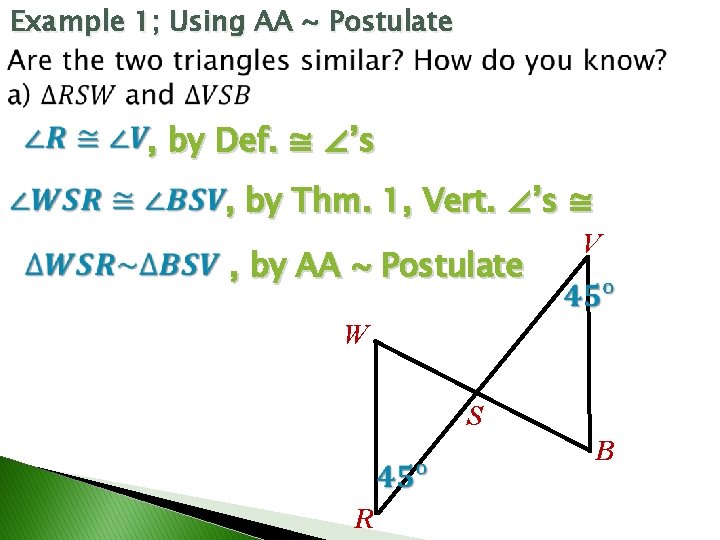
Example 1; Using AA ~ Postulate , by Def. ≅ ∠’s , by Thm. 1, Vert. ∠’s ≅ , by AA ~ Postulate V W S B R

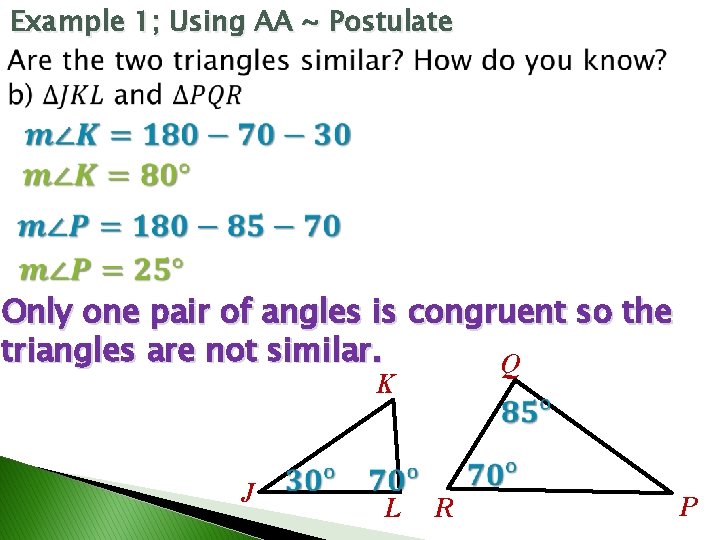
Example 1; Using AA ~ Postulate Only one pair of angles is congruent so the triangles are not similar. Q K J L R P

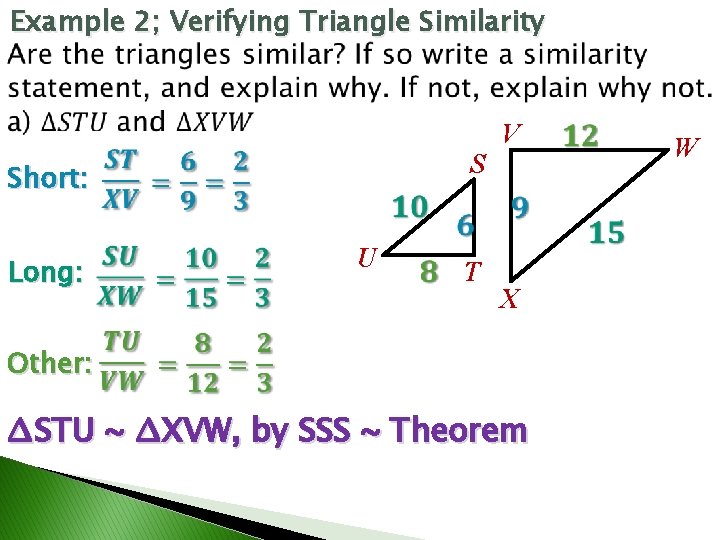
Example 2; Verifying Triangle Similarity S Short: Long: U T V X Other: ∆STU ~ ∆XVW, by SSS ~ Theorem W

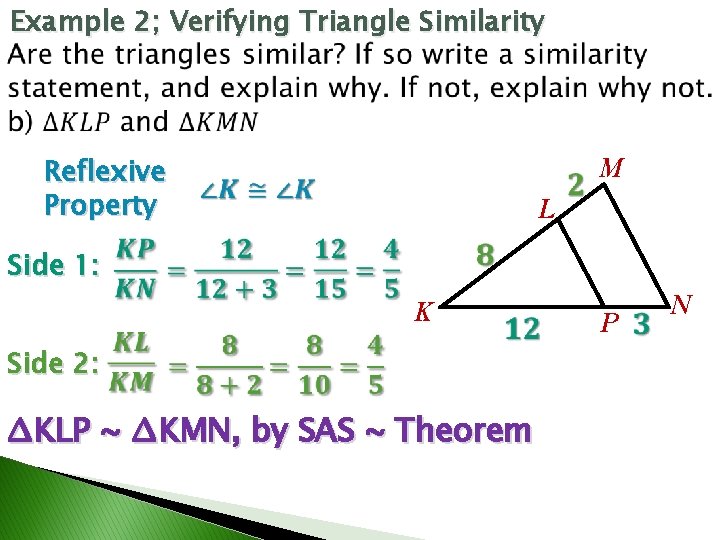
Example 2; Verifying Triangle Similarity Reflexive Property M L Side 1: K Side 2: ∆KLP ~ ∆KMN, by SAS ~ Theorem P N

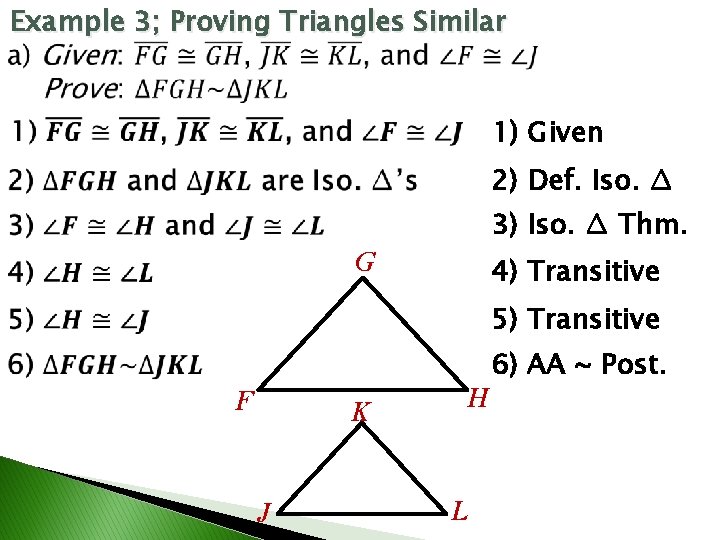
Example 3; Proving Triangles Similar 1) Given 2) Def. Iso. ∆ 3) Iso. ∆ Thm. G 4) Transitive 5) Transitive F K J H L 6) AA ~ Post.

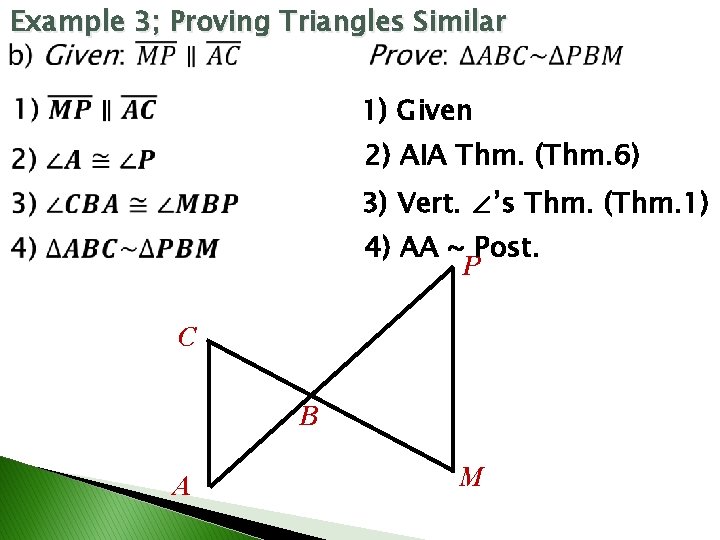
Example 3; Proving Triangles Similar 1) Given 2) AIA Thm. (Thm. 6) 3) Vert. ∠’s Thm. (Thm. 1) 4) AA ~ Post. P C B A M

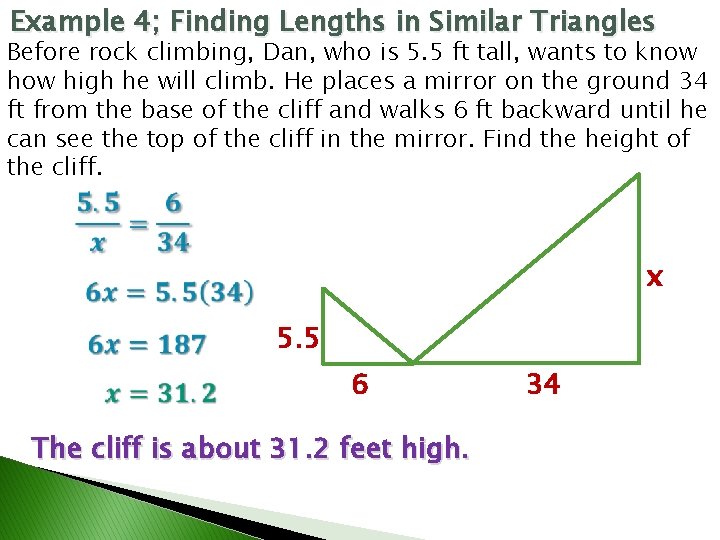
Example 4; Finding Lengths in Similar Triangles Before rock climbing, Dan, who is 5. 5 ft tall, wants to know high he will climb. He places a mirror on the ground 34 ft from the base of the cliff and walks 6 ft backward until he can see the top of the cliff in the mirror. Find the height of the cliff. x 5. 5 6 The cliff is about 31. 2 feet high. 34

#38: Prove Similar Triangles Ø Questions? Ø Summarize Notes Ø Homework Ø Quiz