Prototyping of Efficient Hardware Algorithms for Data Compression

Prototyping of Efficient Hardware Algorithms for Data Compression in Future Communication System Amar Mukherjee, N. Motgi C. Habermann A. Friebe. J. Becker M. Glesner Dept. of Computer Science Schoolf of EECS, University of Central Florida, Orlando, Fl. , U. S. A. Institute of Microelectronic Systems, Darmstadt University of Technology, Darmstadt, Germany Email: amar@cs. ucf. edu becker@mes. tu-darmstadt. de 1

Organization l l l Introduction and Motivation Suffix Tree and Suffix Array BWT compression algorithm and lexicographic sorting A High level description of the algorithm The overall architecture Weavesort Algorithm The basic cell and its operation The opeartion of the machine FPGA platform, Virtex chip Prototyping BWT hardware Algorithm. Simulation results and estimated speed. Future work 2

Communications Systems Requirements Rapid data Transmission with Efficient Utilization of Available Bandwidth => 1. Hardware implementation of communication functions 2. Send as little data as possible => Data Compression 3. FPGA allows experimenting with new ideas and 4. architectures: high speed, high density, low cost, low power, reconfigurable architectures to replace traditional DSP hardware => So. C. 3

Suffix Sorting Suffix sorting finds an array of pointers of suffixes of a string of characters which have been sorted lexicographically. Example: 0 1 2 3 4 5 Memory addresses a b a a b c Character String (a<b<c) Answer: (2, 0, 3, 1, 4, 5) corresponding to suffixes aabc abc baabc bc c 4

Application of Suffix Trees • Exact substring(s) matching problem • Approximate pattern matching • Text search and retrieval • DNA common ancestor problem • Text compression LZ family PPM family BWT ( Burrows-Wheeler Transform) 5

Burrows-Wheeler-Transform l Create all cyclic permutations of the input string. l Sort them lexicographically. l Output the last character of each permutation, and the position of the original text in the sorted table. 6

Burrows-Wheeler-Transform Source text: cacbcaabca l aabcacacbc 0 abcacacbca 1 acacbcaabc 2 acbcaabcac 3 bcaabcacac 4 bcacacbcaa 5 caabcacacb 6 cacacbcaab 7 cacbcaabca 8 <- original cbcaabcaca 9 l l Output: cacccabbaa, 8 7

Reversing the Burrows-Wheeler Transformed input: cacccabbaa, 8 l Table: left side: sorted, right side: original a(1) -> c(1) 0 a(2) -> a(1) 1 a(3) -> c(2) 2 a(4) -> c(3) 3 b(1) -> c(4) 4 Output: b(2) -> a(2) 5 cacbcaabca c(1) -> b(1) 6 c(2) -> b(2) 7 c(3) -> a(3) 8 <c(4) -> a(4) 9 l 8

BWT back-end Move-to-front encoding(MTF): l Input: cacccabbaa, 8, Alphabet: abc l 2, cab 1, acb 1, cab 0, cab 1, acb 2, bac 0, bac 1, abc 0, abc l Output: 2110012010, 8 l 9

BWT back-end l MTF l Input: 2110012010, 8 l Encode MTF output string using Huffman code, add position (‘ 8’) to output in binary. 10

Bzip 2 l Run-length encoding l Burrows-Wheeler-Transform l Modified Move-To-Front-Encoding l Huffman encoding 11

A High Level Description of the Algorithm with an Example 0 1 2 3 4 5 Memory addresses a b a a b c Character String (a<b<c) 023 14 5 (a a a ) (b b) (c) bab ac 2 03 (a) ( b b) a c Next characters 1 4 5 (a) (c) - - - Next Characters 2 0 3 1 4 5 -> Suffix Array (a) (c) 12

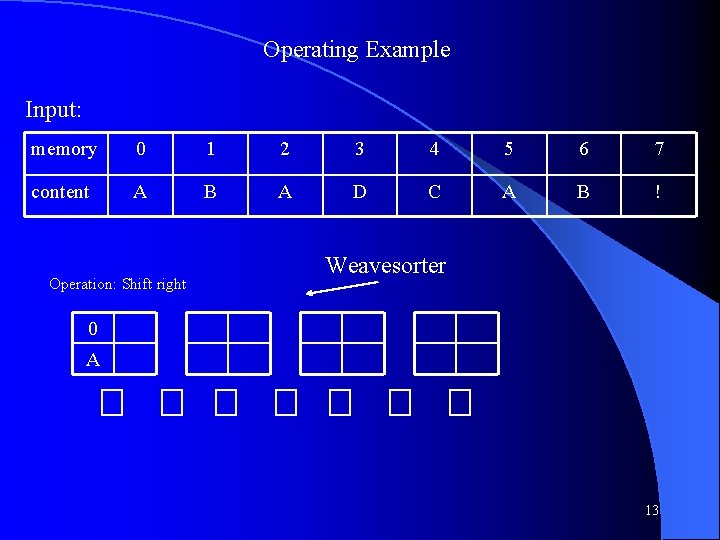
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift right Weavesorter 0 A 13

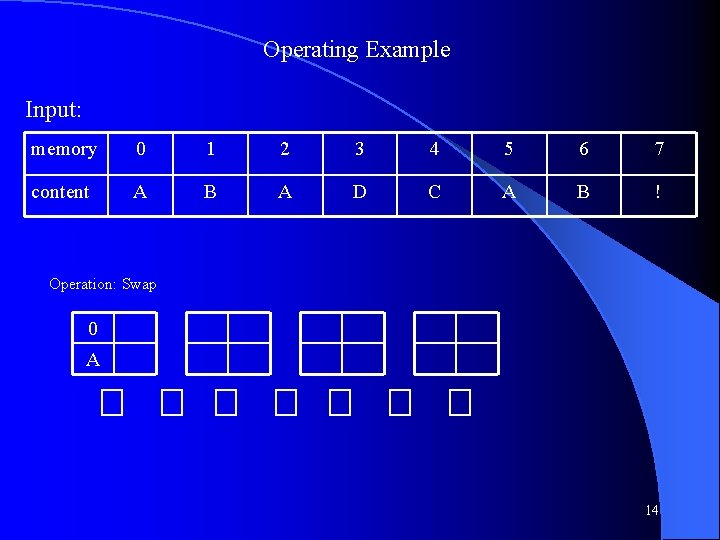
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 0 A 14

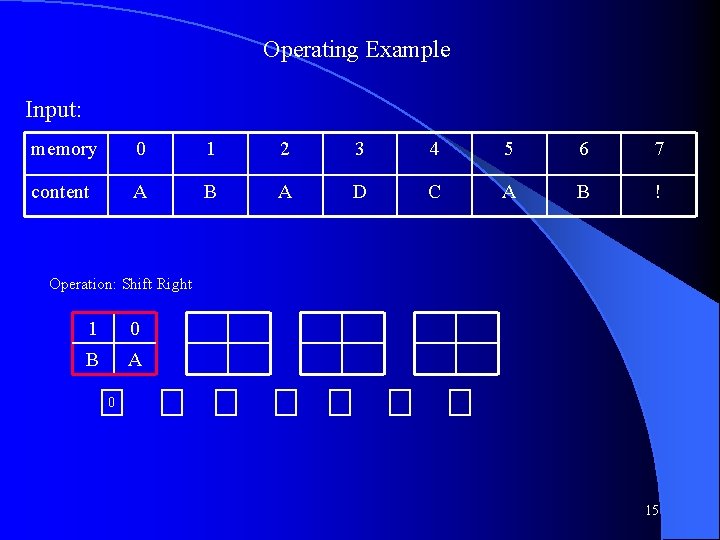
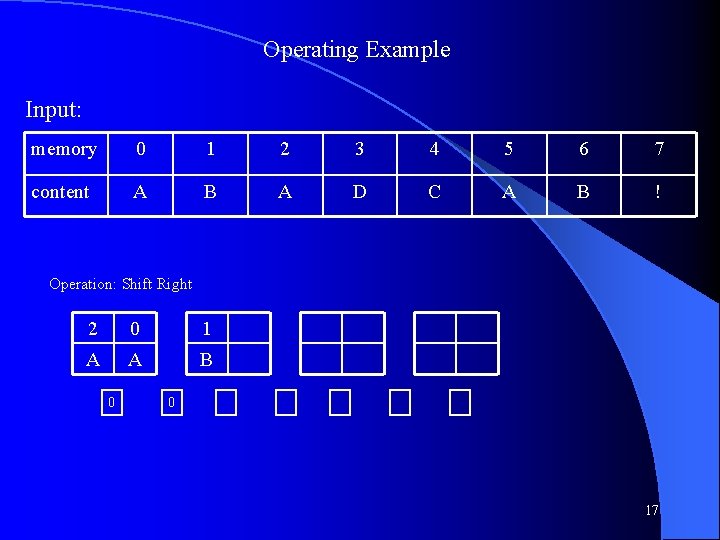
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Right 1 0 B A 0 15

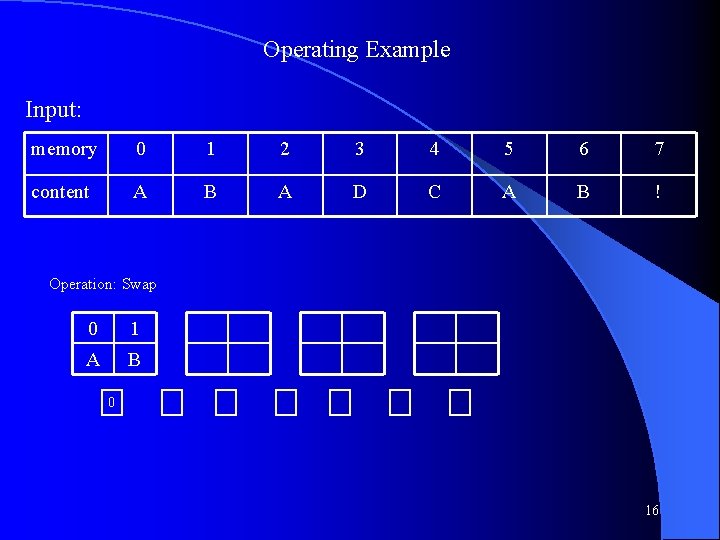
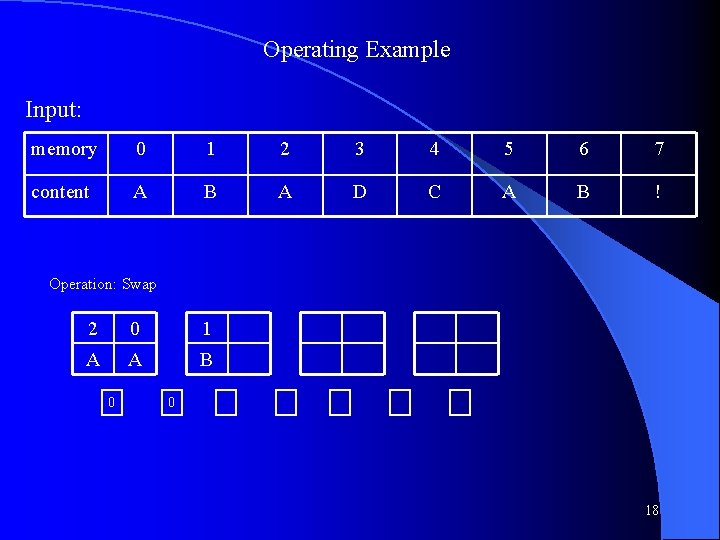
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 0 1 A B 0 16

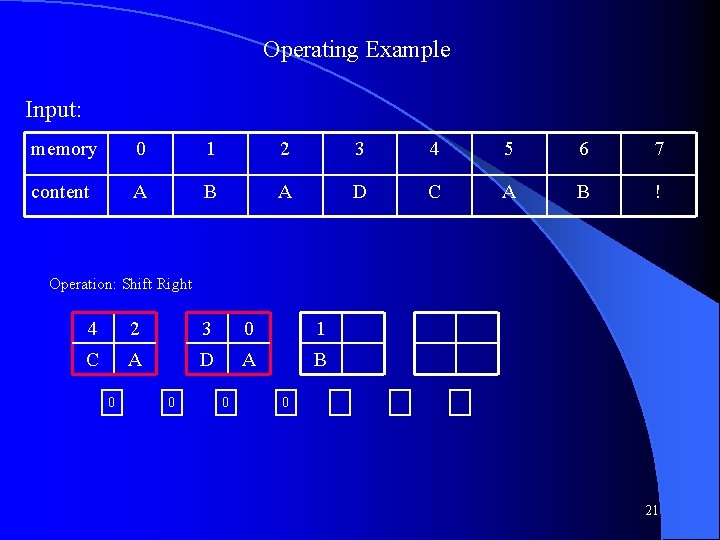
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Right 2 0 1 A A B 0 0 17

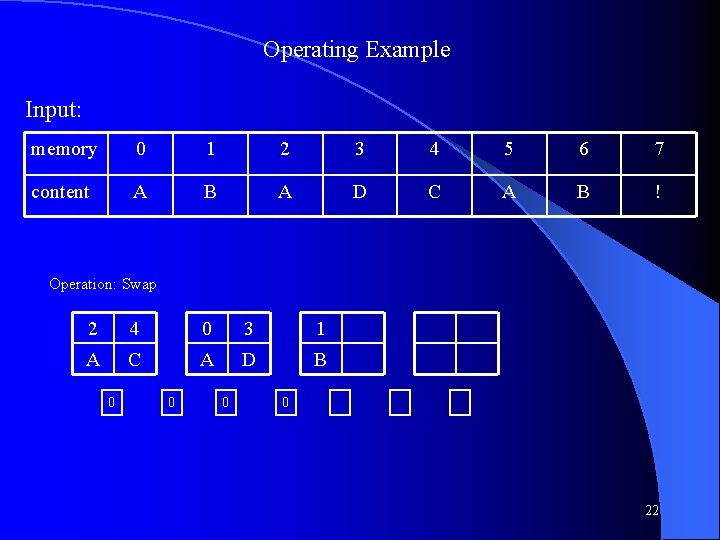
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 2 0 1 A A B 0 0 18

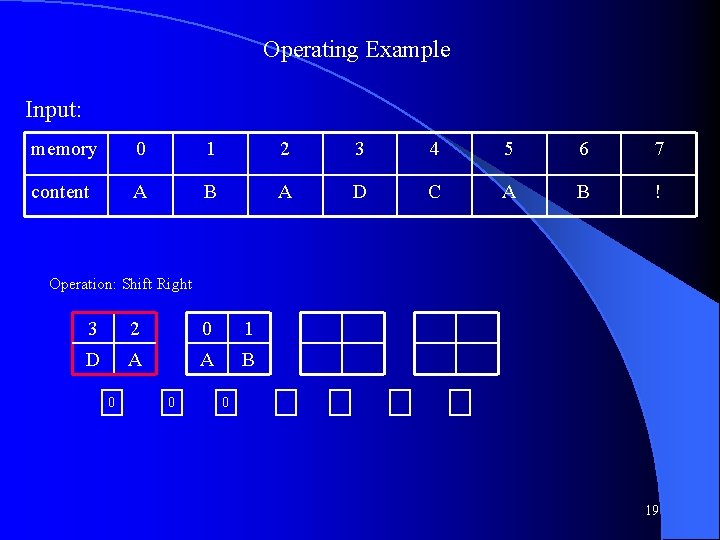
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Right 3 2 0 1 D A A B 0 0 0 19

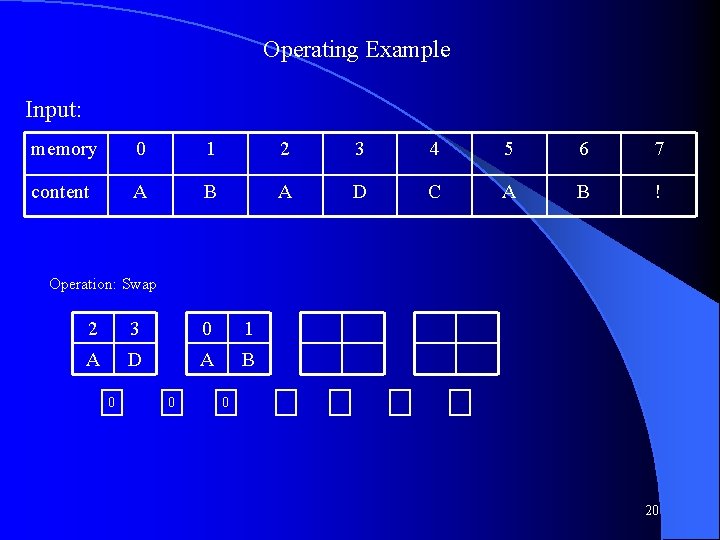
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 2 3 0 1 A D A B 0 0 0 20

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Right 4 2 3 0 1 C A D A B 0 0 21

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 2 4 0 3 1 A C A D B 0 0 22

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Right 5 4 2 0 3 1 A C A A D B 0 0 0 23

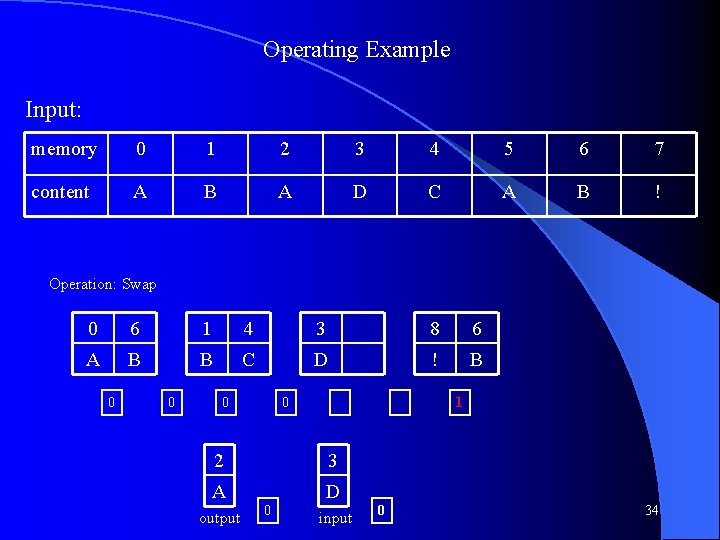
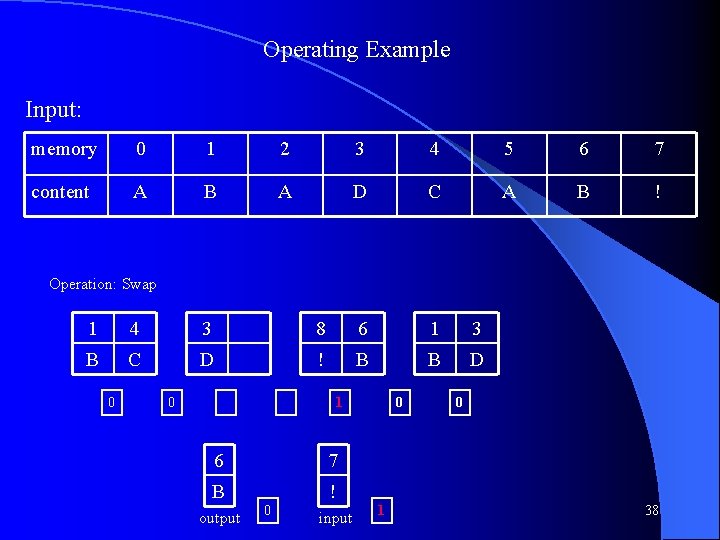
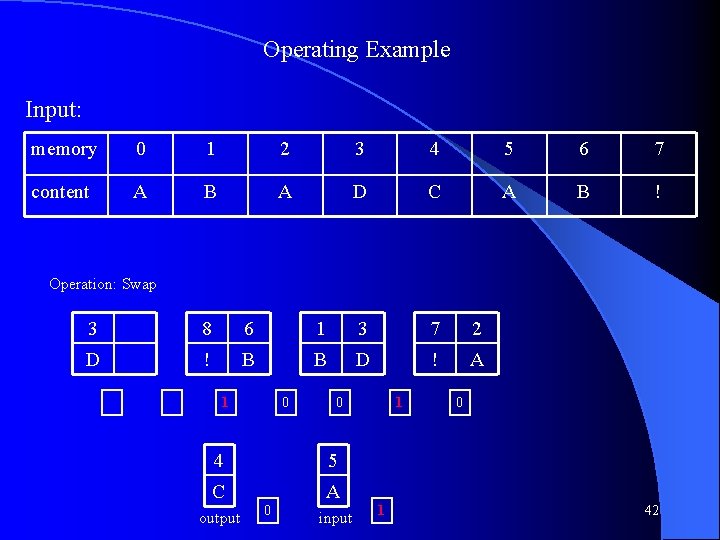
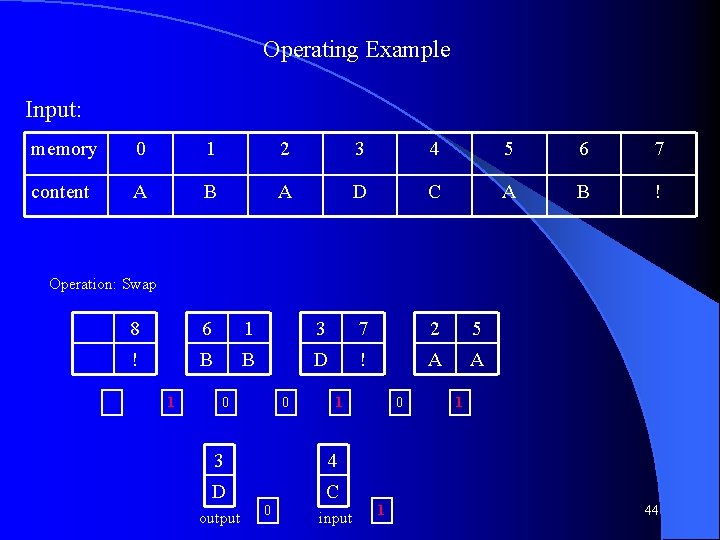
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 5 4 2 0 1 3 A C A A B D 0 0 0 24

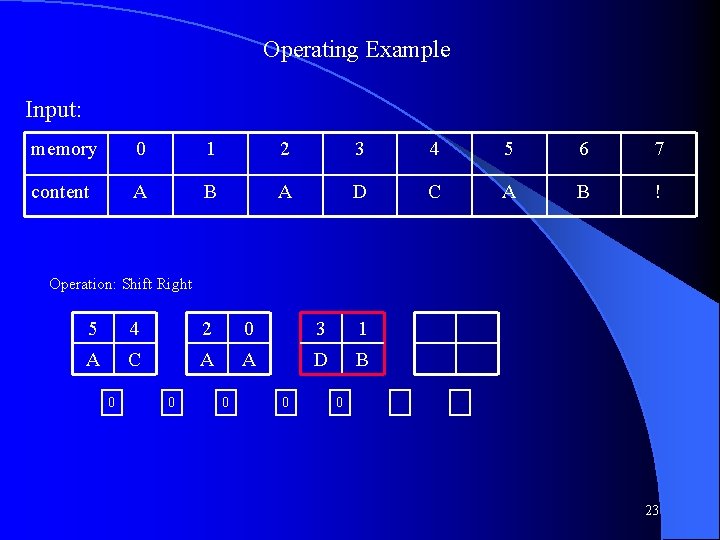
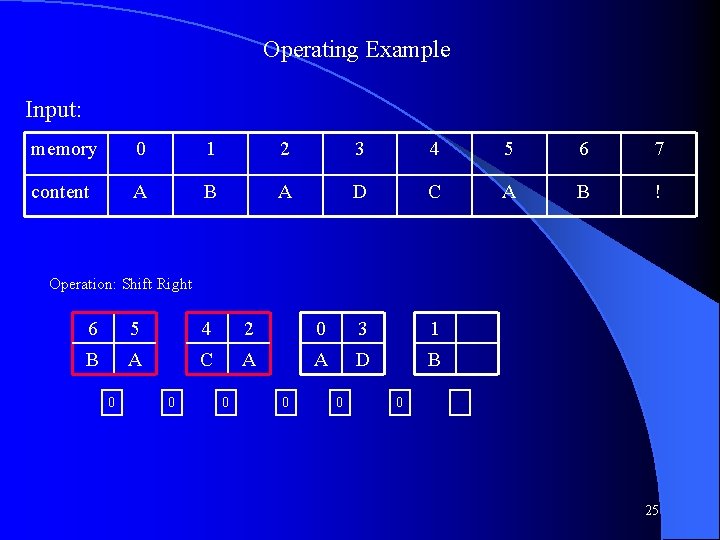
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Right 6 5 4 2 0 3 1 B A C A A D B 0 0 0 25

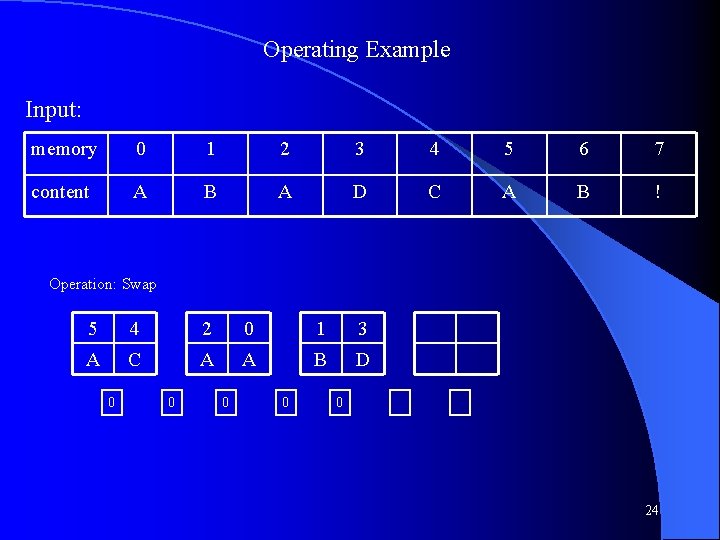
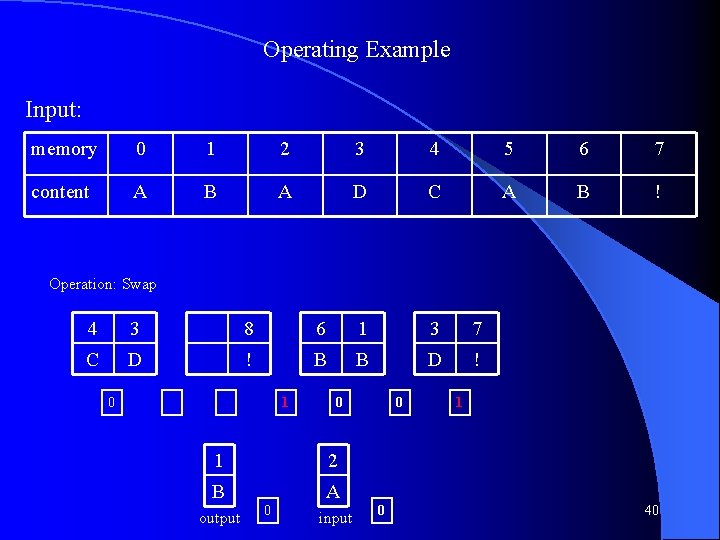
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 5 6 2 4 0 3 1 A B A C A D B 0 0 0 26

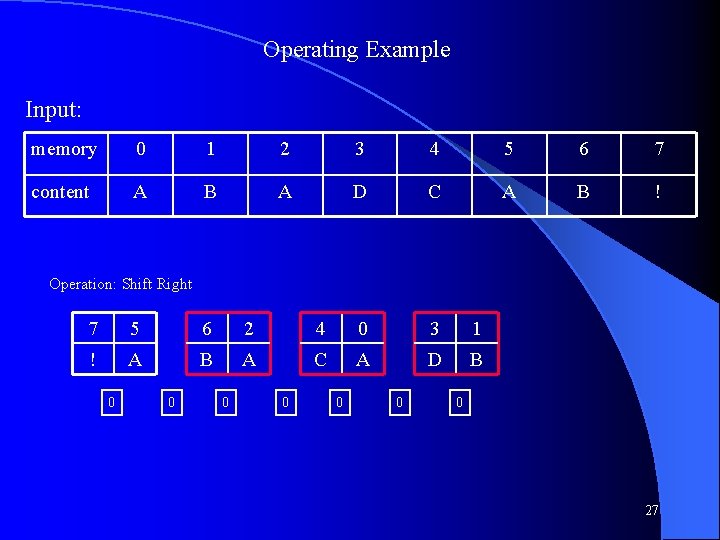
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Right 7 5 6 2 4 0 3 1 ! A B A C A D B 0 0 0 0 27

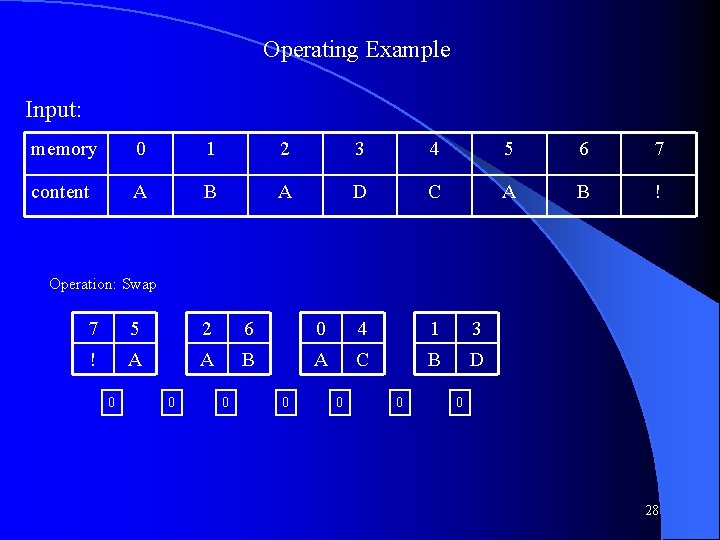
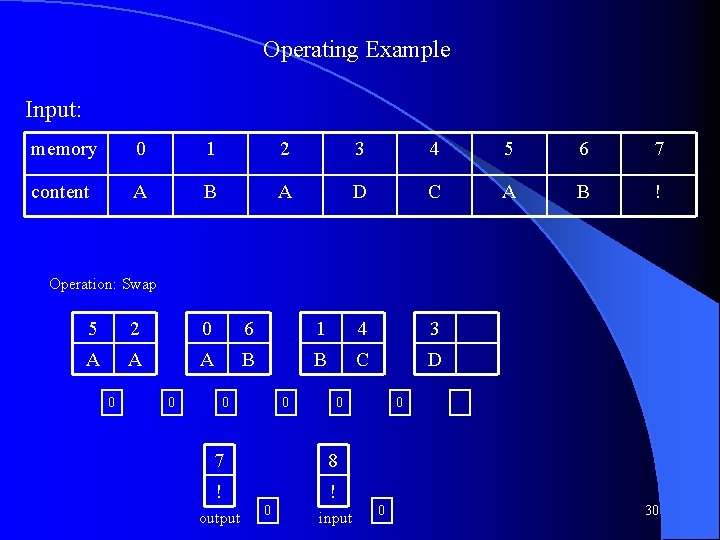
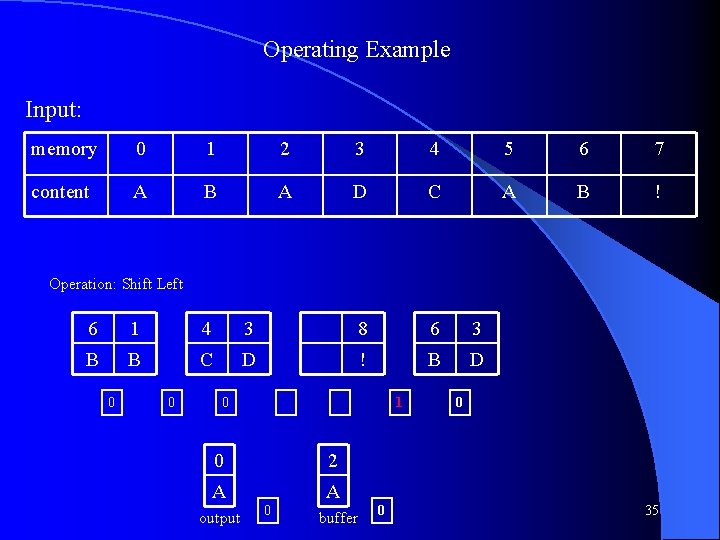
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 7 5 2 6 0 4 1 3 ! A A B A C B D 0 0 0 0 28

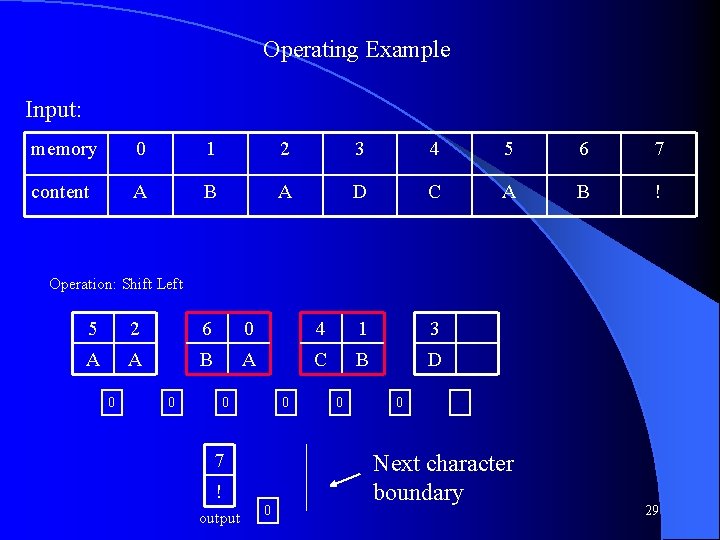
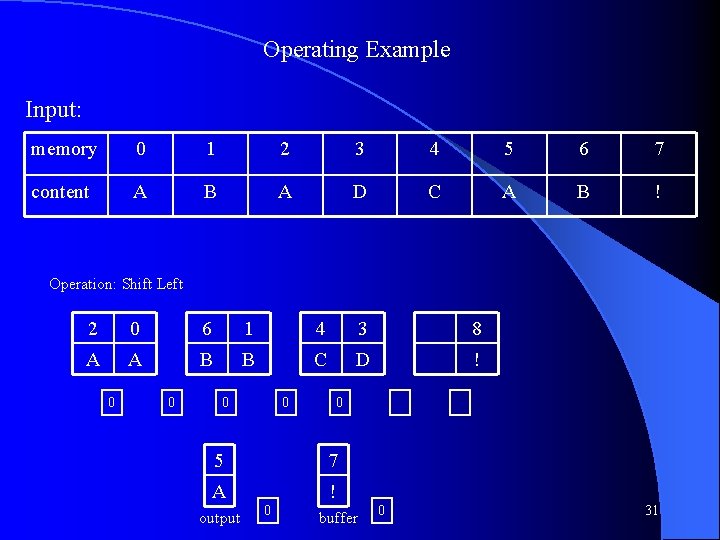
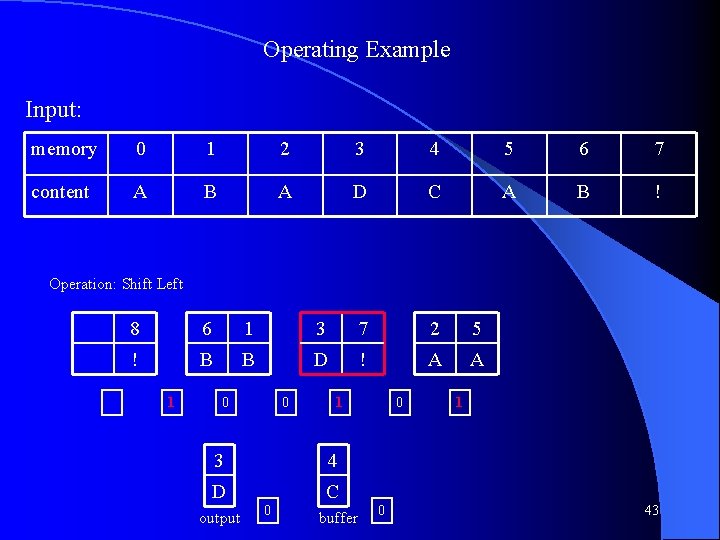
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 5 2 6 0 4 1 3 A A B A C B D 0 0 7 ! output 0 0 0 Next character boundary 29

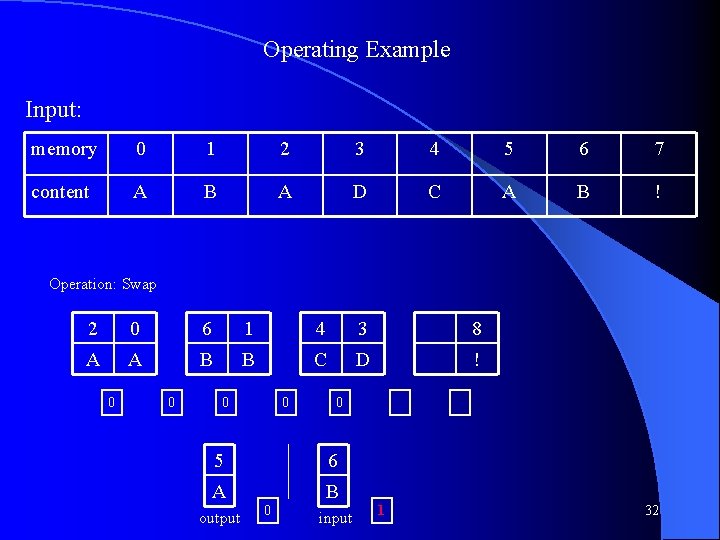
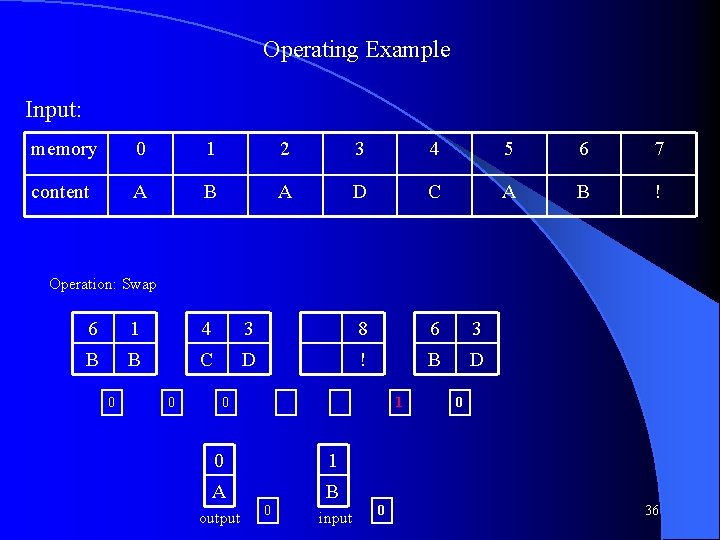
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 5 2 0 6 1 4 3 A A A B B C D 0 0 0 7 8 ! ! output 0 input 0 0 30

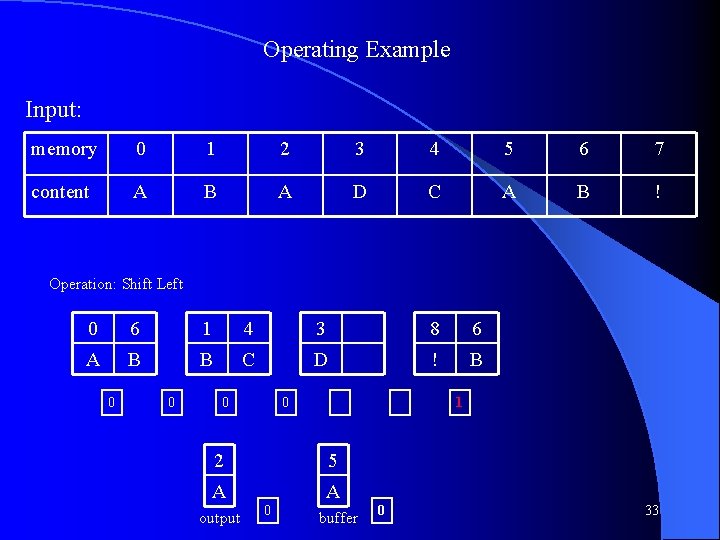
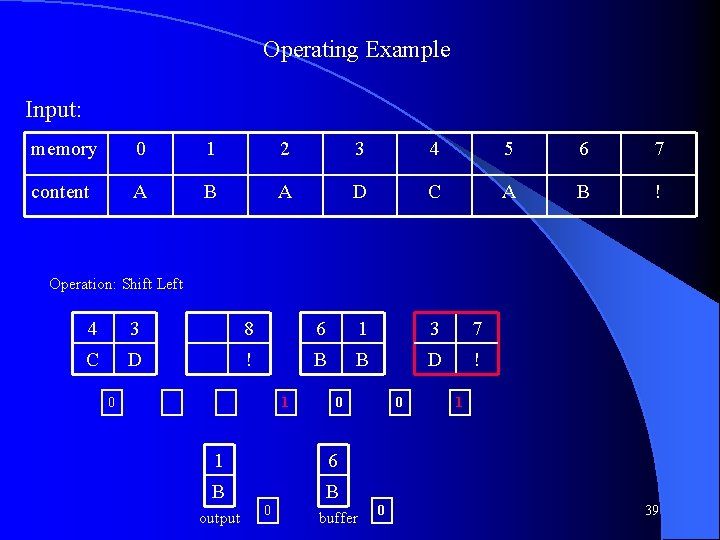
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 2 0 6 1 4 3 8 A A B B C D ! 0 0 0 5 7 A ! output 0 buffer 0 31

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 2 0 6 1 4 3 8 A A B B C D ! 0 0 0 5 6 A B output 0 input 1 32

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 0 6 1 4 3 8 6 A B B C D ! B 0 0 1 2 5 A A output 0 buffer 0 33

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 0 6 1 4 3 8 6 A B B C D ! B 0 0 1 2 3 A D output 0 input 0 34

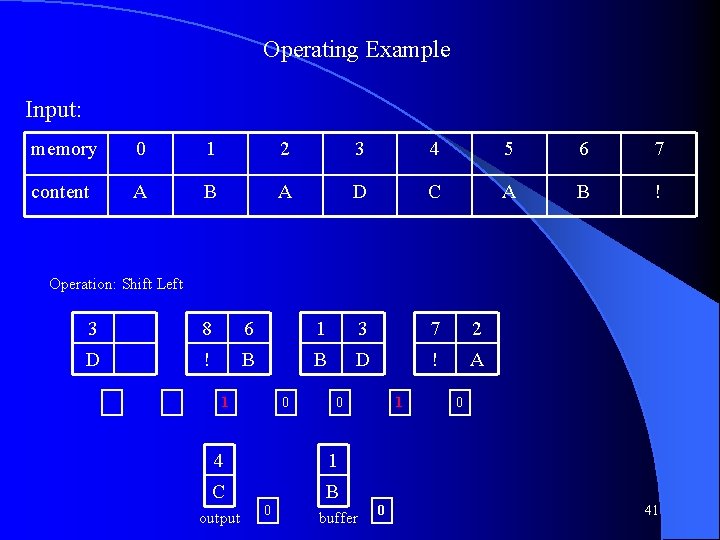
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 6 1 4 3 8 6 3 B B C D ! B D 0 0 0 1 0 2 A A output 0 buffer 0 0 35

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 6 1 4 3 8 6 3 B B C D ! B D 0 0 0 1 A B output 0 input 0 0 36

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 1 4 3 8 6 3 1 B C D ! B D B 0 0 1 6 0 B A output 0 buffer 0 0 0 37

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 1 4 3 8 6 1 3 B C D ! B B D 0 0 1 6 7 B ! output 0 input 0 1 0 38

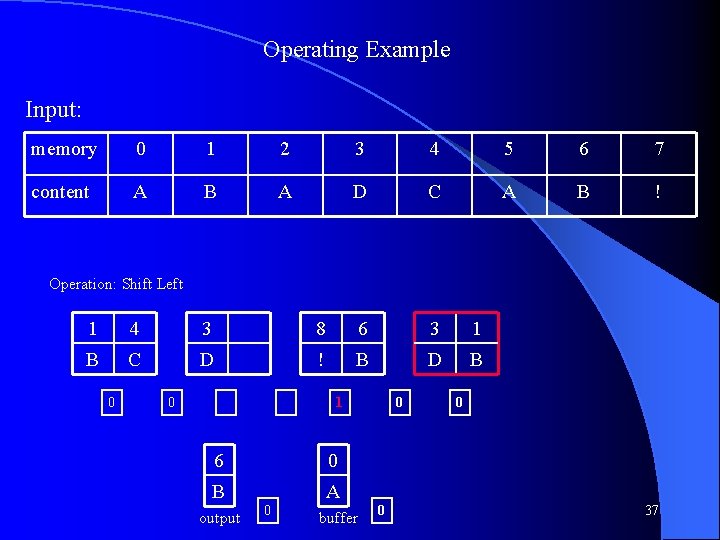
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 4 3 8 6 1 3 7 C D ! B B D ! 0 1 6 B B output 0 buffer 0 0 1 39

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 4 3 8 6 1 3 7 C D ! B B D ! 0 1 2 B A output 0 input 0 0 1 40

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 3 8 6 1 3 7 2 D ! B B D ! A 1 0 0 4 1 C B output 0 buffer 1 0 0 41

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 3 8 6 1 3 7 2 D ! B B D ! A 1 0 0 4 5 C A output 0 input 1 1 0 42

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 8 6 1 3 7 2 5 ! B B D ! A A 1 0 0 1 3 4 D C output 0 buffer 0 0 1 43

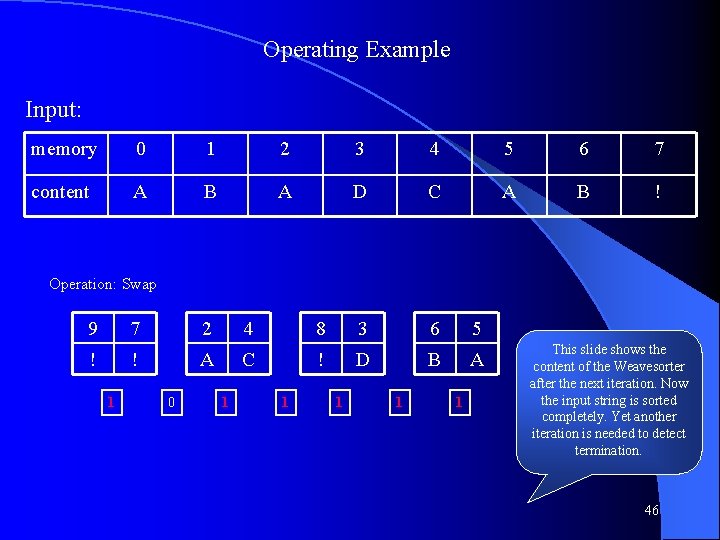
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 8 6 1 3 7 2 5 ! B B D ! A A 1 0 0 1 3 4 D C output 0 input 0 1 1 44

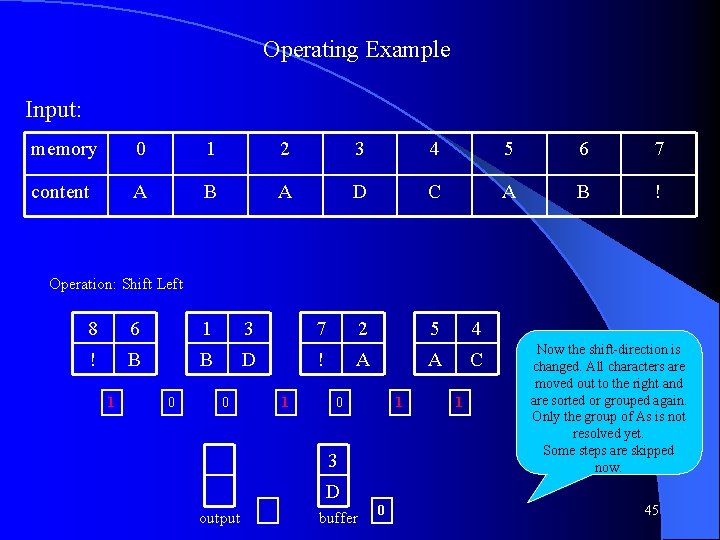
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Shift Left 8 6 1 3 7 2 5 4 ! B B D ! A A C 1 0 0 1 3 1 Now the shift-direction is changed. All characters are moved out to the right and are sorted or grouped again. Only the group of As is not resolved yet. Some steps are skipped now. D output buffer 0 45

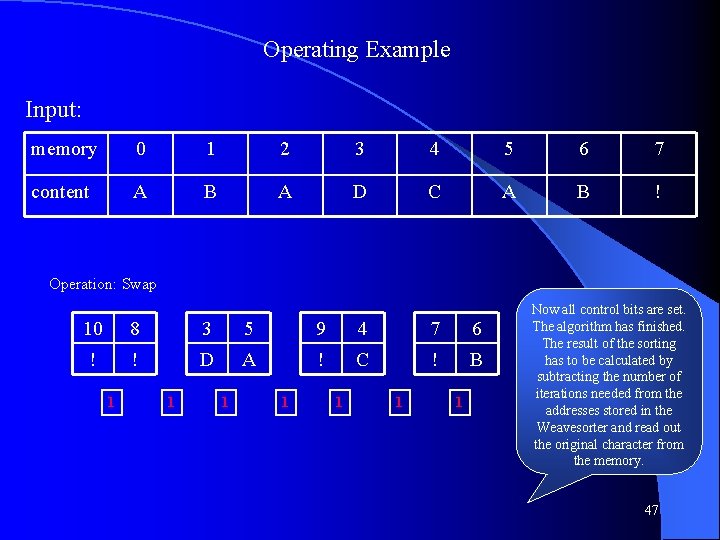
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 9 7 2 4 8 3 6 5 ! ! A C ! D B A 1 0 1 1 1 This slide shows the content of the Weavesorter after the next iteration. Now the input string is sorted completely. Yet another iteration is needed to detect termination. 46

Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 10 8 3 5 9 4 7 6 ! ! D A ! C ! B 1 1 1 1 Now all control bits are set. The algorithm has finished. The result of the sorting has to be calculated by subtracting the number of iterations needed from the addresses stored in the Weavesorter and read out the original character from the memory. 47

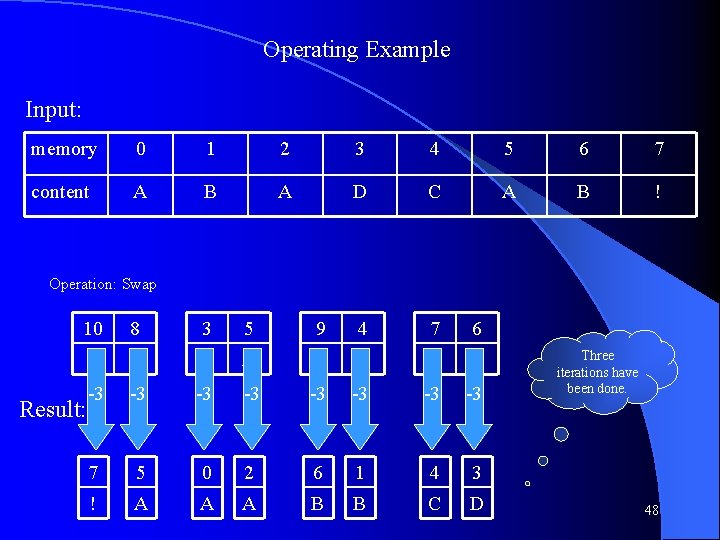
Operating Example Input: memory 0 1 2 3 4 5 6 7 content A B A D C A B ! Operation: Swap 10 8 3 5 9 4 7 6 ! ! D A ! C ! B -3 -3 7 5 0 2 6 1 4 3 ! A A A B B C D Result: Three iterations have been done. 48

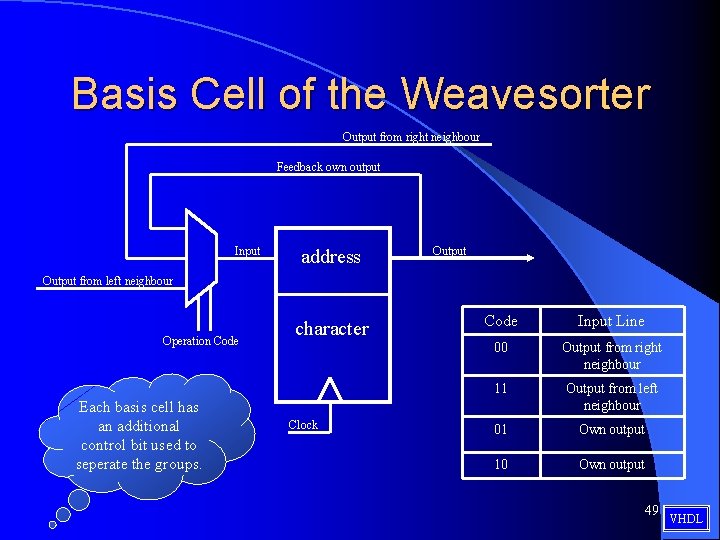
Basis Cell of the Weavesorter Output from right neighbour Feedback own output Input address Output from left neighbour Operation Code Each basis cell has an additional control bit used to seperate the groups. character Clock Code Input Line 00 Output from right neighbour 11 Output from left neighbour 01 Own output 10 Own output 49 VHDL

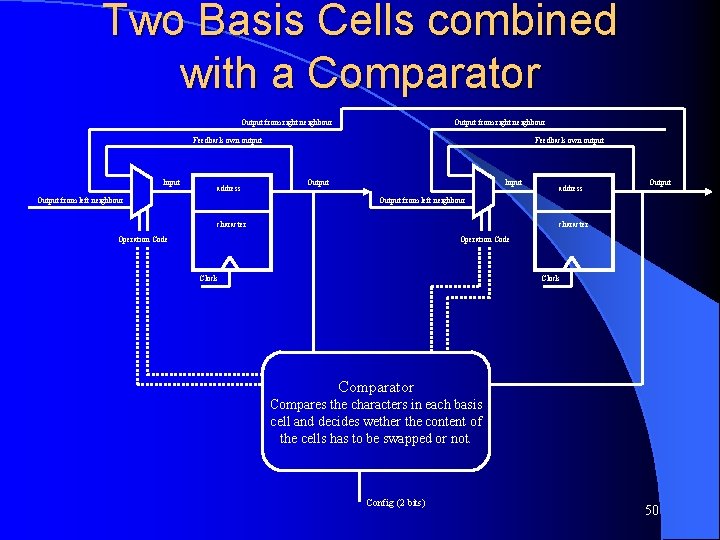
Two Basis Cells combined with a Comparator Output from right neighbour Feedback own output Input address Output from left neighbour Feedback own output Output Input address Output from left neighbour character Operation Code Clock Comparator Compares the characters in each basis cell and decides wether the content of the cells has to be swapped or not. Config (2 bits) 50

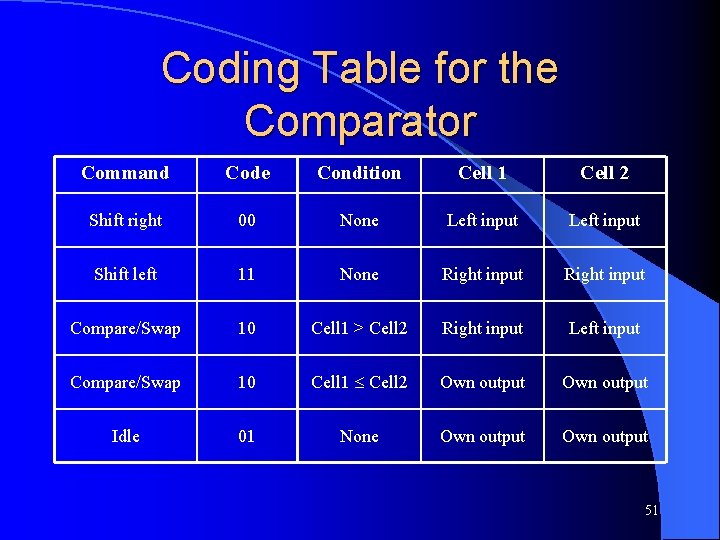
Coding Table for the Comparator Command Code Condition Cell 1 Cell 2 Shift right 00 None Left input Shift left 11 None Right input Compare/Swap 10 Cell 1 > Cell 2 Right input Left input Compare/Swap 10 Cell 1 Cell 2 Own output Idle 01 None Own output 51

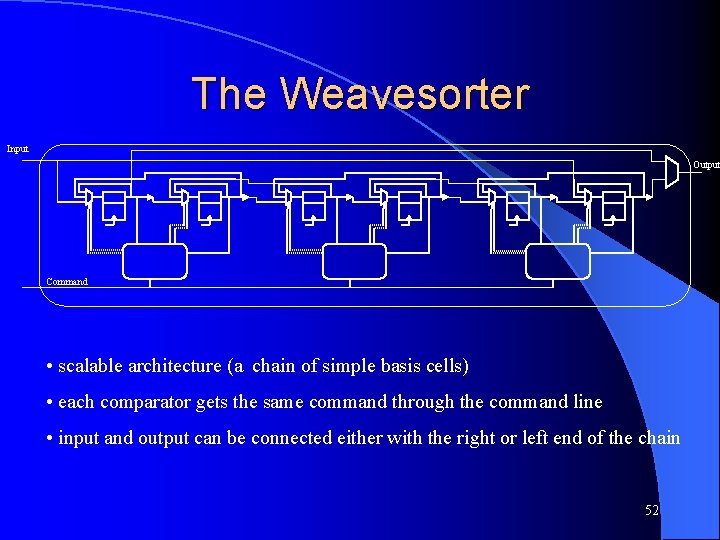
The Weavesorter Input Output Command • scalable architecture (a chain of simple basis cells) • each comparator gets the same command through the command line • input and output can be connected either with the right or left end of the chain 52

VHDL Description of the Basis Cell The basis cell contains a register and a 3: 1 input multiplexer with two configuration bits. Mux_Reg <= Shift. R_In_Reg when Config = "00" else -- shift-right Shift. L_In_Reg when Config = "11" else -- shift-left Out_Reg; -- stay in cell 53

VHDL description of the Comparator Control. Logic: process(Char_Cell 1, Char_Cell 2, Config_In) begin case Config_In is when "00" => Config_Out_Cell 1 <= "00"; Config_Out_Cell 2 <= "00"; when "11" => Config_Out_Cell 1 <= "11"; Config_Out_Cell 2 <= "11"; -- shift_right -- shift_left when "10" => -- compare if ctrl_Cell 1 = '0' and (Char_Cell 1 > Char_Cell 2) then Config_Out_Cell 1 <= "11"; Config_Out_Cell 2 <= "00"; else Config_Out_Cell 1 <= "01"; Config_Out_Cell 2 <= "01"; end if; when others => Config_Out_Cell 1 <= "01"; Config_Out_Cell 2 <= "01"; -- if anything else the value of the -- registers is stored end case; end process Control. Logic; 54

VHDL description of the Weavesorter (I) The Weavesorter is generated in a generate loop. The first and the last cell must be treated differently. begin -- a. Sorter cells : for i in length*2+1 downto 0 generate -- the first cell is connected with the input and the output ------------ first : if i = 0 generate cell_first : e. Cell generic map (adr_width, char_width) port map (Clk => Clk, Shift. R_In_Reg => Input(adr_width+char_width-1 downto 0), Shift. L_In_Reg => Out_Reg(i+1), Config => config_cell(i), Out_Reg => Out_Reg(i)); end generate first; 55

VHDL description of the Weavesorter (II) The cells in between are connected with their neighbours. -- each middle cell is connected to its neighbours ---------------- middle : if i > 0 and i < length*2+1 generate cell_middle : e. Cell generic map (adr_width, char_width) port map (Clk => Clk, Shift. R_In_Reg => Out_Reg(i-1), Shift. L_In_Reg => Out_Reg(i+1), Config => config_cell(i), Out_Reg => Out_Reg(i)); end generate middle; 56

VHDL description of the Weavesorter (III) The last cell is connected to the input and the output of the Weavesorter -- last cell is connected to the Input and the Output ------------last : if i = length*2+1 generate cell_last : e. Cell generic map (adr_width, char_width) port map (Clk => Clk, Shift. R_In_Reg => Out_Reg(i-1), Shift. L_In_Reg => Input(adr_width+char_width-1 downto 0), Config => config_cell(i), Out_Reg => Out_Reg(i)); end generate last; end generate cells; 57

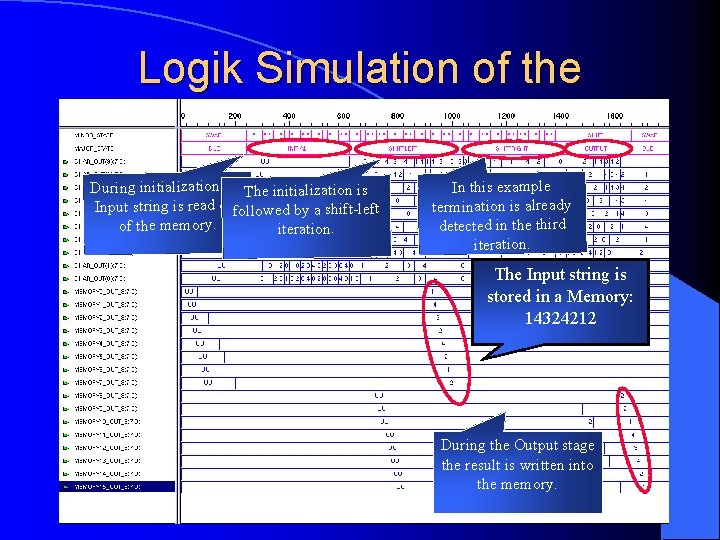
Logik Simulation of the Weavesorter During initialization the. The initialization is Input string is read outfollowed by a shift-left of the memory. iteration. In this example termination is already detected in the third iteration. The Input string is stored in a Memory: 14324212 During the Output stage the result is written into the memory. 58

Trends l XILINX l l l Virtex FPGA Up to 3. 2 million system gates Up to 804 single-ended I/Os or 244 differential I/O pair 622 Mbps differential I/O performance Over 311 Mbps single-ended I/O performance Support for 20 I/O standards Power supply: 1. 8 V 0. 18 m process six-layer metal silicon process System Performance up to 200 MHz Built-in clock-managementcircuitry Hierarchical memory system 59

Trends 60

Trends l PCI Prototyping Board Source: Nallatech Limited 61

ownload directly to the Xilinx hardware device(s) with unlimited reconfigurations* !! 3 XC 4000 62 Reconfigurable Hardware: Design Flow

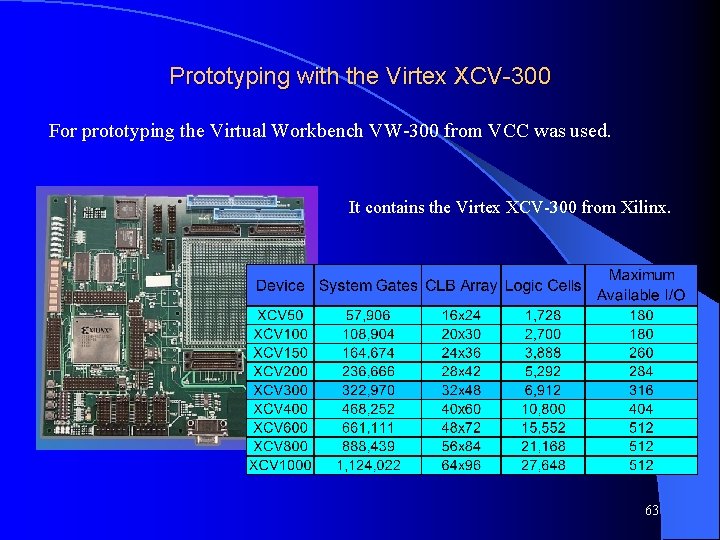
Prototyping with the Virtex XCV-300 For prototyping the Virtual Workbench VW-300 from VCC was used. It contains the Virtex XCV-300 from Xilinx. 63

Prototyping Results Rapid Prototyping on Virtex XCV 300 Weavesorter Architecture with 100 cells Resource Allocation Performance Percentage of used FPGA slices Post Place & Route Simulation 88% used Min. Critical Path Delay = 22 ns => Max. Clock Rate 45 MHz In addition to mapping this 100 cells weavesortert on the FPGA we also developed a test environment on the virtual workbench. The environment uses the 8 character display on the workbench to write back result of the BWT transformation. The input is provided with the eight dip-switches on the board. 64