Protonneutron and pairing interactions A titanic struggle of

Proton-neutron and pairing interactions A titanic struggle of good vs. good to determine what nuclei do R. F. Casten WNSL, Yale Lecture 2 July, 2009

Next 2 -ish lectures • Preliminaries – The independent particle model – nucleons in a box, confinement and quantization, Pauli Principle, and magic numbers. • Residual interactions – the key to answering the riddle of the universe. –Pairing vs the p-n interaction: what, how, why? Relation to nuclear shapes. –How to measure p-n interaction strengths –What to do with those numbers once you have them. Answer: LOTS !!! (See, for example, Dennis’ Martin’s theses. )

TINSTAASQ While I don’t mind hearing myself talk, these lectures are actually for YOU So, please ask questions if stuff isn’t clear.

Simple Observables - Even-Even (cift-cift). . Nuclei 1000 4+ 400 2+ 0 0+ Masses E (ke. V) Jπ For Odd-A nuclei, also the angular momentum of the ground state.

First, some background – The independent particle model and the magic numbers Without them, we would be very sad Basic idea is that nucleons move around the nucleus in orbits determined by a common force or potential acting on all of them

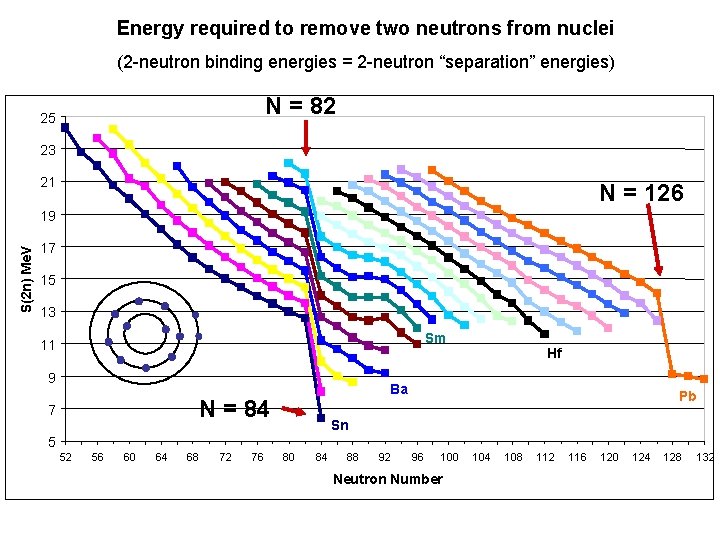
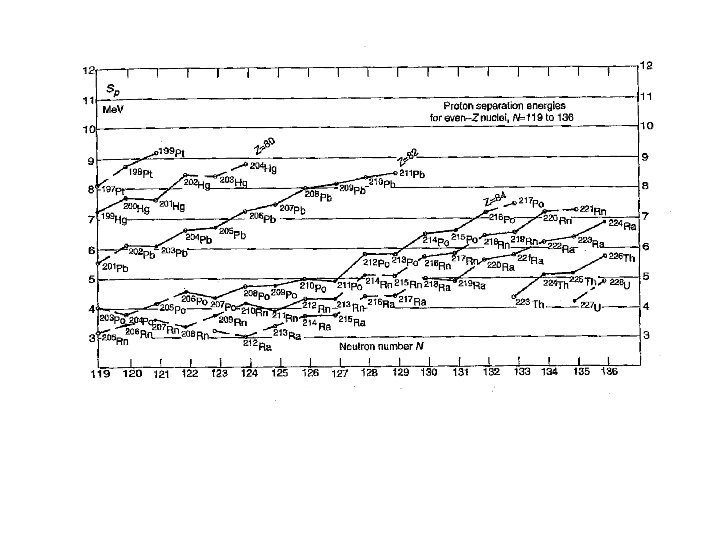
Energy required to remove two neutrons from nuclei (2 -neutron binding energies = 2 -neutron “separation” energies) N = 82 25 23 21 N = 126 S(2 n) Me. V 19 17 15 13 Sm 11 9 Ba N = 84 7 Hf Pb Sn 5 52 56 60 64 68 72 76 80 84 88 92 96 100 Neutron Number 104 108 112 116 120 124 128 132

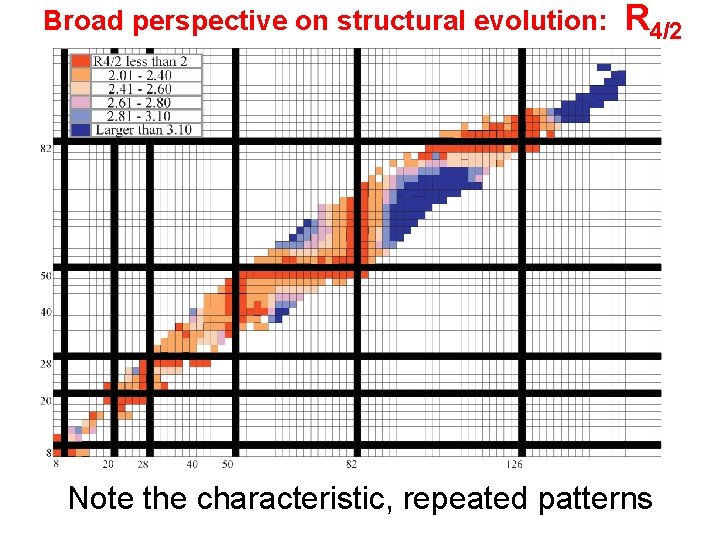
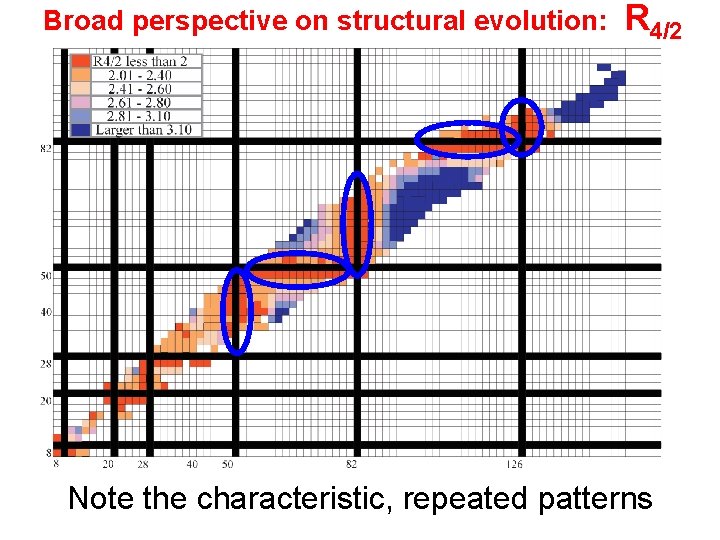
Broad perspective on structural evolution: R 4/2 Note the characteristic, repeated patterns

Independent particle model: magic numbers, shell structure, valence nucleons. Three key ingredients First: Vij Ui r = |ri - rj| Nucleon-nucleon force – very complex ~ r One-body potential – very simple: Particle in a box This extreme approximation cannot be the full story. Will need “residual” interactions. But it works surprisingly well in special cases.

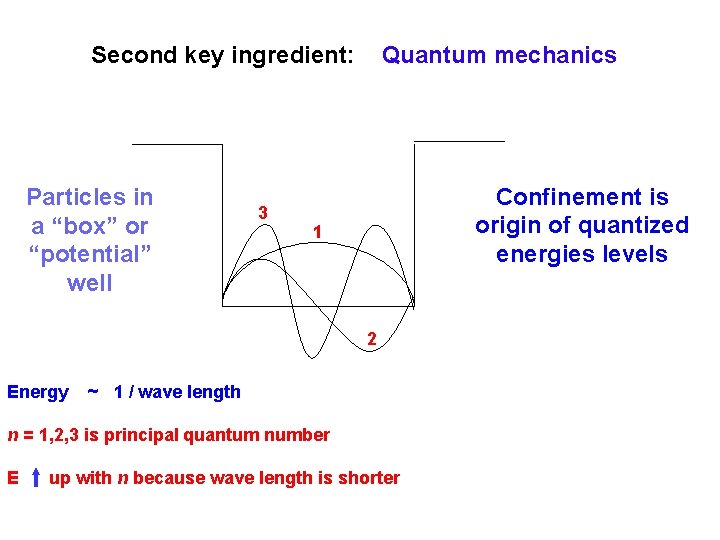
Second key ingredient: Particles in a “box” or “potential” well 3 Quantum mechanics Confinement is origin of quantized energies levels 1 2 Energy ~ 1 / wave length n = 1, 2, 3 is principal quantum number E up with n because wave length is shorter

Tw o qu an t n um an n d um l b er s, Total angular momentum of a nucleon is j=l+-½ Such a state has 2 j + 1 magnetic substates, m.

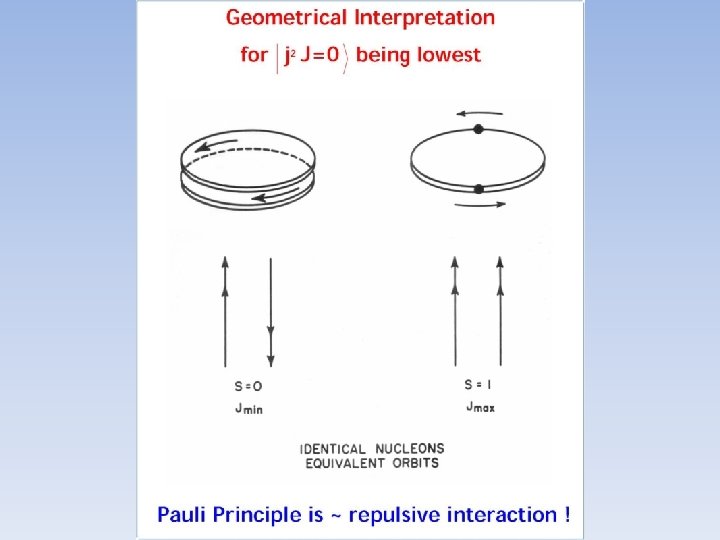
Third key ingredient Pauli Principle • Two fermions, like two protons or two neutrons, can NOT be in the same place at the same time: can NOT occupy the same orbit. • Orbit with total Ang Mom, j, has 2 j + 1 substates, hence can only contain 2 j + 1 neutrons or protons. This, plus the clustering of levels in simple potentials, gives nuclear SHELL STRUCTURE

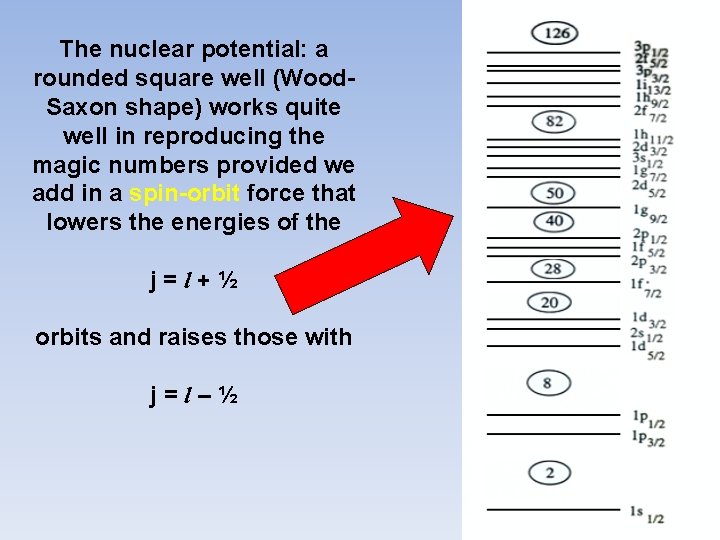
The nuclear potential: a rounded square well (Wood. Saxon shape) works quite well in reproducing the magic numbers provided we add in a spin-orbit force that lowers the energies of the j=l+½ orbits and raises those with j=l–½

The empirical magic numbers near stability • 2, 8, 20, 28, (40), 50, (64), 82, 126 • These numbers, and a couple of “R 4/2” values, are the only things I will ask you to memorize.

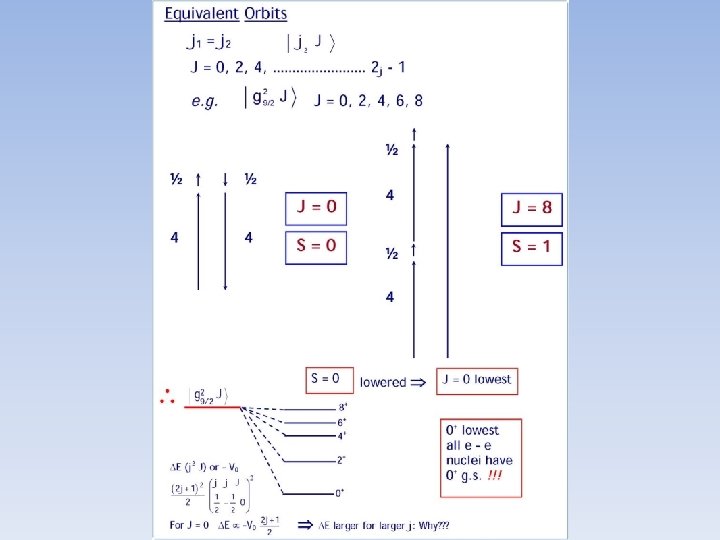
How to use the Independent Particle Model • Put nucleons (protons and neutrons separately) into orbits. • Special case: Put 2 j + 1 identical nucleons (fermions) in an orbit with angular momentum j. Each one MUST go into a different magnetic substate. Remember, angular momenta add vectorially but projections (m values) add algebraically. • So, total M is sum of m’s M = j + (j – 1) + (j – 2) +. . . + 1/2 + (-1/2) +. . . + [ - (j – 2)] + [ - (j – 1)] + (-j) M = 0. If the only possible M is 0, then J= 0 Thus, a full j- shell, and hence a full major shell of nucleons, always has total angular momentum 0. This simplifies things enormously !!! It allows us to often consider only the valence nucleons!

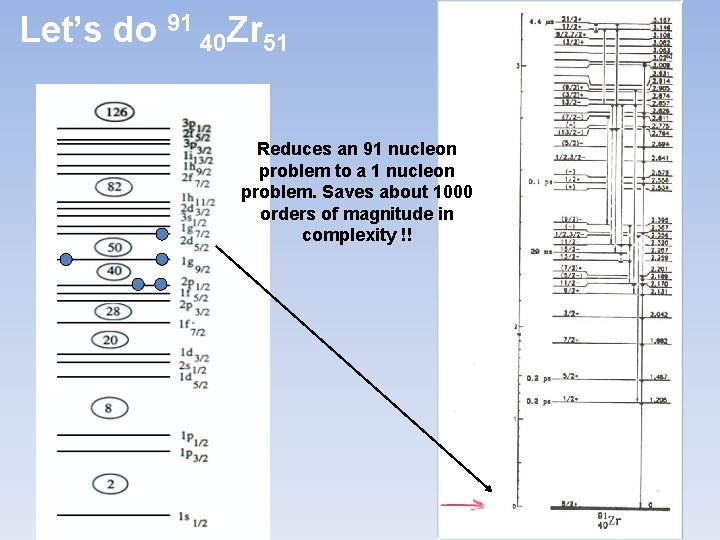
Let’s do 91 40 Zr 51 Reduces an 91 nucleon problem to a 1 nucleon problem. Saves about 1000 orders of magnitude in complexity !!

What happens when we have more than one “valence“ nucleon? Ind. Part. model too crude. Need to add extra interactions among valence nucleons. H = H 0 + Hresid. These dominate the evolution of structure

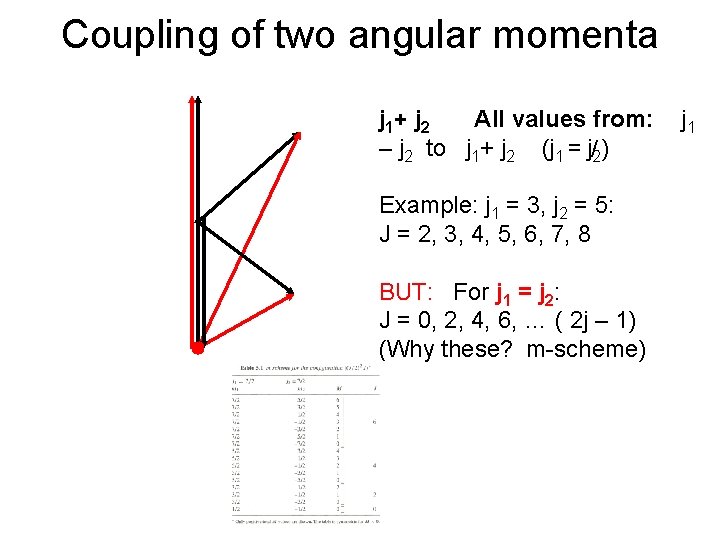
Coupling of two angular momenta j 1+ j 2 All values from: – j 2 to j 1+ j 2 (j 1 = j/2) Example: j 1 = 3, j 2 = 5: J = 2, 3, 4, 5, 6, 7, 8 BUT: For j 1 = j 2: J = 0, 2, 4, 6, … ( 2 j – 1) (Why these? m-scheme) j 1

How can we predict these energies? • Need only two ingredients: – Nuclear force is short range and attractive – Pauli Principle • Lets assume a d force that acts ONLY when the two particles are in contact. • Later, we will talk about the pairing interaction, which is very similar.

x

This is the most important slide: understand this and all the key ideas about residual interactions will be clear !!!!!

R 4/2< 2. 0 Another way to look at the results. Remember, everything depended on the angle between the angular momentum vectors (orbital planes) of the two particles. So, it turns out that the results we have can be expressed in terms of a nice simple formula in terms of those angles.

“Magic plus 2”: Characteristic spectra This, ultimately, is why all e-e nuclei have Yaaaaaaaaaay !!!! 0+ ground states !!!!!!! ~ 1. 3 -ish

Broad perspective on structural evolution: R 4/2 Note the characteristic, repeated patterns

Pairing interaction An alternate short range force Pairing vs. d spectra

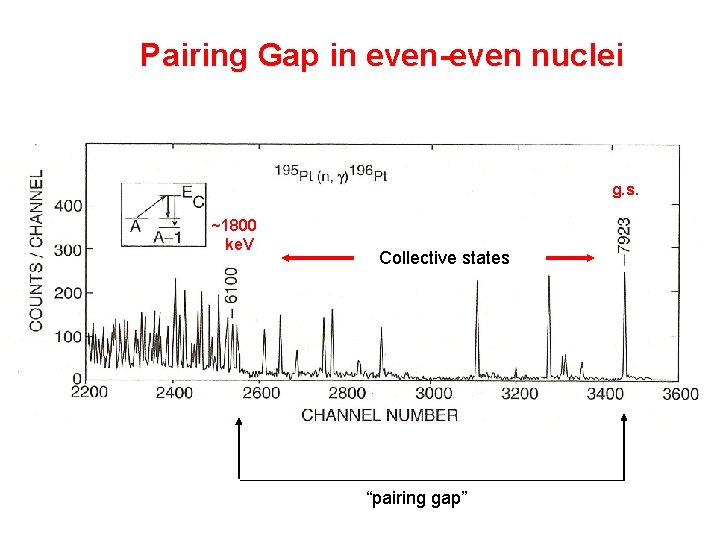
Evidence for “Pairing” • Ground states of even-even nuclei with 2 particles outside a doubly magic nucleus have J=0+ with energy much lower than other states. Related: Ground states of ALL even-even nuclei have J = 0+ • Even-even nuclei are more bound than odd-A nuclei. (Note: the above are related to the energies of 0+ states relative to states of OTHER spins in the same configuration, and are similar to the effects of any short range interaction. The next relates to the energy of the lowest 0+ state relative to all other states) • Nuclei far from closed shells show a large spacing (~ 2 Me. V) between the gs and other non-collective states: the “pairing gap”. • Note: These two sets of experimental features of nuclei are very different. How can we understand them by the concept of pairing?

Pairing Gap in even-even nuclei g. s. ~1800 ke. V Collective states “pairing gap”

Pairing gap in Sn

Pairing: what it is and what it does • Short range force between identical nucleons. • As with any short range force, it favors coupling two nucleons in identical orbits to J =/ 0. • Pairing force drives nuclei towards spherical shapes – J = 0 has no preferred direction in space. • That is a “diagonal” effect on the energies. There also strong mixing effects that are extraordinarily important. -- Pairing produces the well-known “pairing gap” in e-e nuclei.

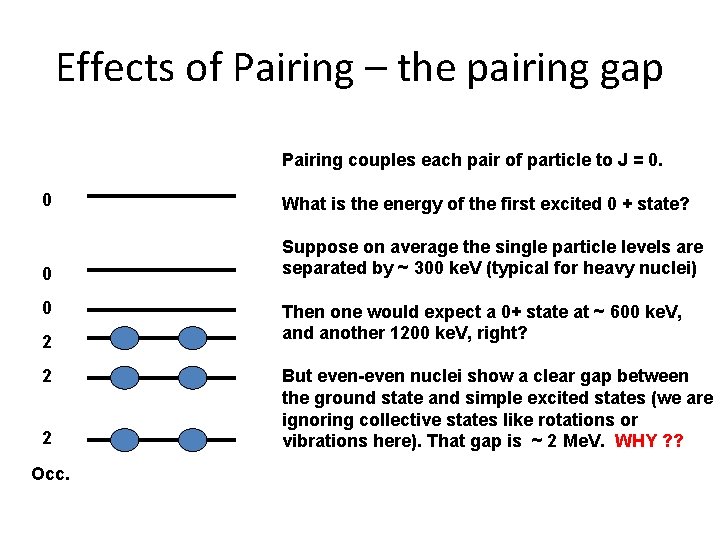
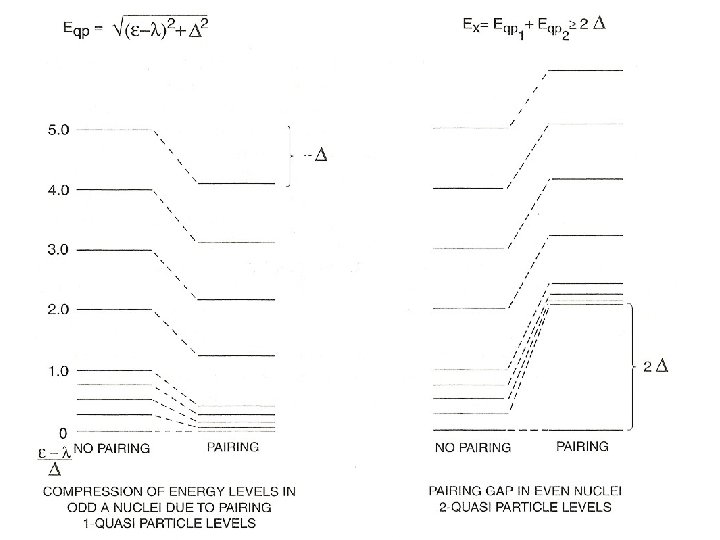
Effects of Pairing – the pairing gap Pairing couples each pair of particle to J = 0. 0 What is the energy of the first excited 0 + state? 0 Suppose on average the single particle levels are separated by ~ 300 ke. V (typical for heavy nuclei) 0 2 2 2 Occ. Then one would expect a 0+ state at ~ 600 ke. V, and another 1200 ke. V, right? But even-even nuclei show a clear gap between the ground state and simple excited states (we are ignoring collective states like rotations or vibrations here). That gap is ~ 2 Me. V. WHY ? ?

Mixing induced by the pairing force • Look at the expression for the pairing force: • What does it do? Suppose all the particles on both sides of the interaction are in the same orbit, that is, j 1 =j 2=j 3=j 4 and these particles couple in pairs to J = 0. • Then < |V| > = -G( j + ½) for J = 0. That is, the energy of the 0+ state is lowered. We have seen that. Many people think that is what pairing is all about. However, that is only part of the story. What else does the matrix element do? • It allows a pair of particles coupled to J = 0 in an orbit j 1 (= j 2) to scatter into a different orbit j 3 ( = j 4), still with angular momentum zero. But what is that effect? It is mixing !!!! The final wave function of the ground state will have a mixture of two particles in j 1 and two in j 2.

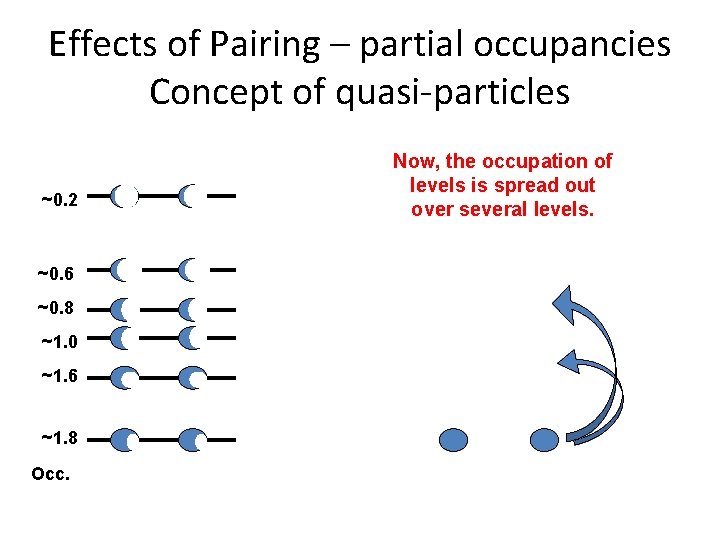
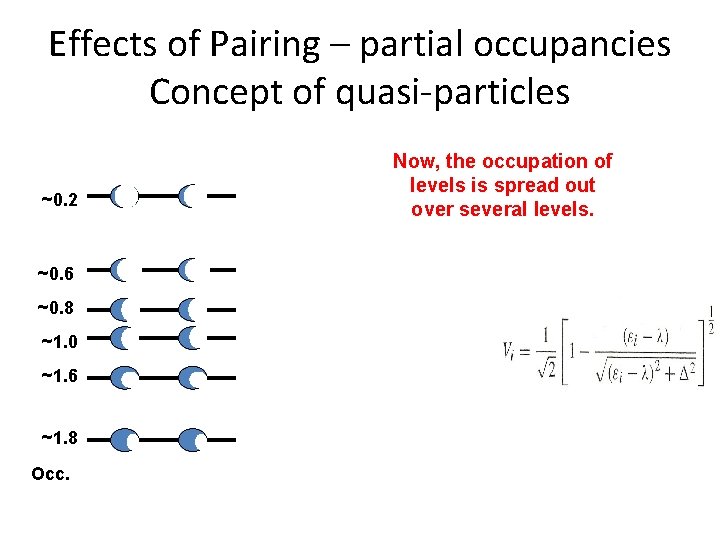
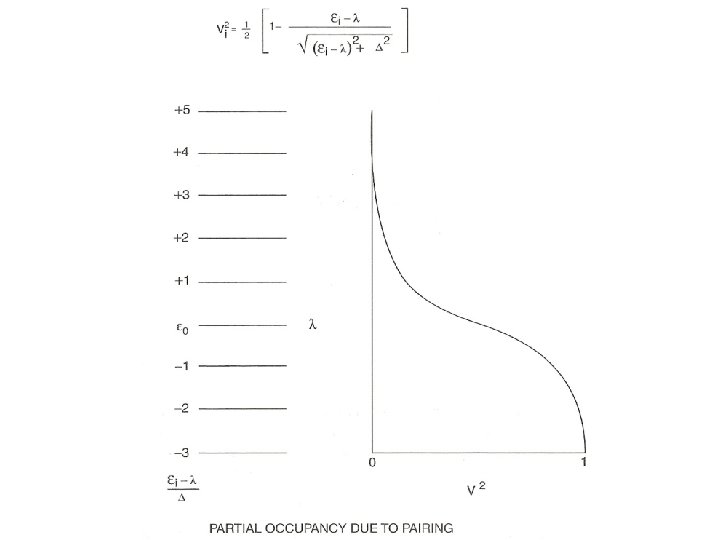
Effects of Pairing – partial occupancies Concept of quasi-particles ~0. 2 ~0. 6 ~0. 8 ~1. 0 ~1. 6 ~1. 8 Occ. Now, the occupation of levels is spread out over several levels.

Single particle energies are replaced with quasi-particle energies involving a “gap” parameter related to the strength of the pairing matrix element. In even-even nuclei the ground state is lowered producing a “pairing gap. Making an excited 0+ state means creating two quasi-particles and so is > 2 D >2 D In odd-even nuclei the excited states are produced by substituting one quasiparticle for another, so they can have very low energies ! So: e-e nuclei – pairing gap: o-e nuclei – energy compression !

Effects of Pairing – partial occupancies Concept of quasi-particles ~0. 2 ~0. 6 ~0. 8 ~1. 0 ~1. 6 ~1. 8 Occ. Now, the occupation of levels is spread out over several levels.

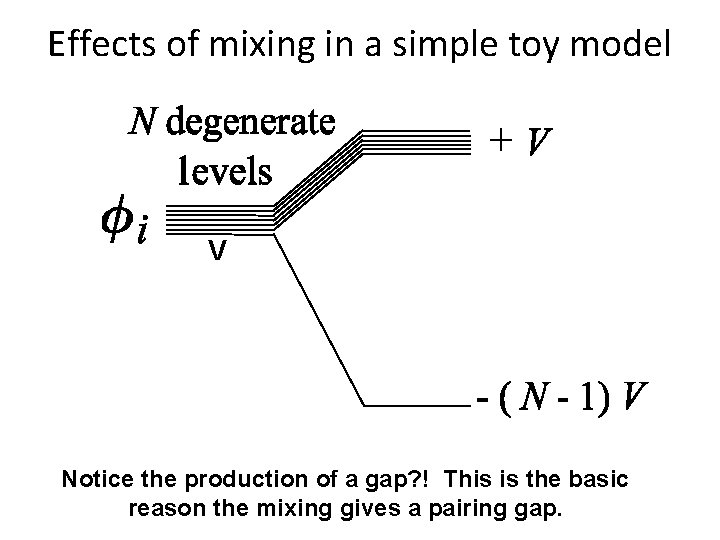
Effects of mixing in a simple toy model V Notice the production of a gap? ! This is the basic reason the mixing gives a pairing gap.

I’ll stop here and discuss the p-n interaction next time along with ways of actually measuring it, and lots of examples, some taken from ISOLTRAP data (!!!!), of what you can learn from it.

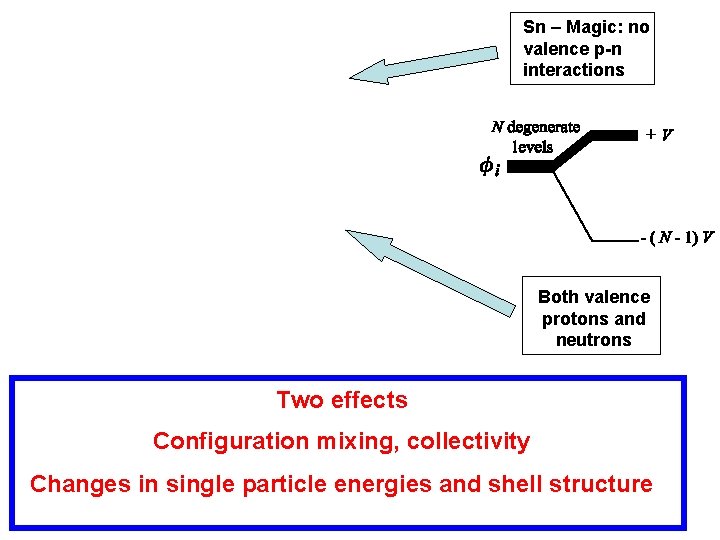
Proton-neutron interaction • Also short range. How do its effects differ? • Favors couplings to both J = 0 and to high J states. Hence drives nuclei toward non-spherical shapes. • Induces configuration mixing in the shell model. • It is, by far, the most important residual interaction in determining collectivity and deformation in nuclei

Sn – Magic: no valence p-n interactions Both valence protons and neutrons Two effects Configuration mixing, collectivity Changes in single particle energies and shell structure

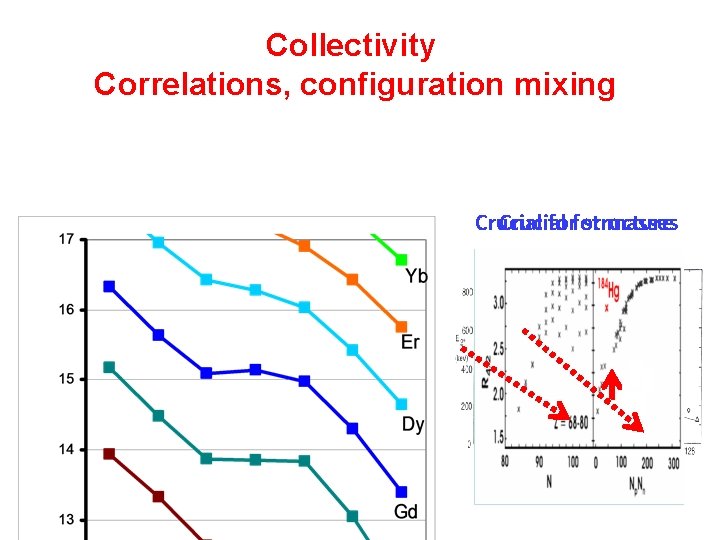
Collectivity Correlations, configuration mixing Crucial forfor structure masses

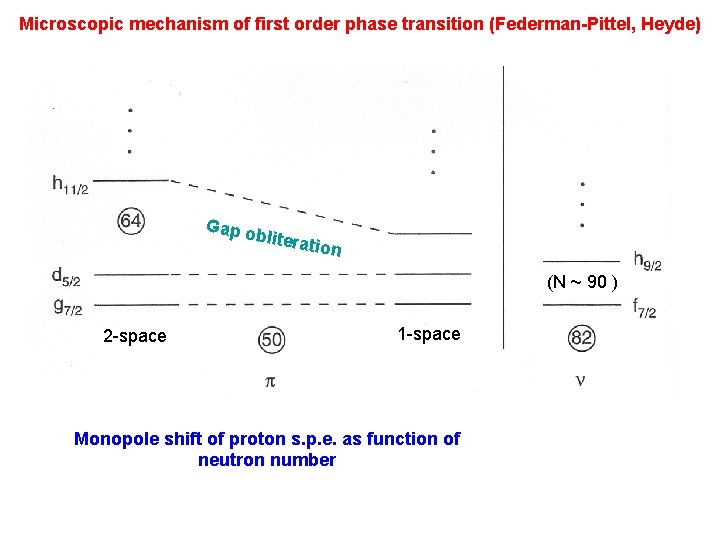
Microscopic mechanism of first order phase transition (Federman-Pittel, Heyde) Gap o blitera tion (N ~ 90 ) 2 -space 1 -space Monopole shift of proton s. p. e. as function of neutron number

Effects of short range p-n interactions in 2 valence particle nuclei – contrast with likenucleon force that we considered above For like nucleons, here we invoked the Pauli Principal to show that the lowest spin state, 0+, came lowest. For unlike particles, protons and neutrons, there is no such restriction and the maximum angular momentum can also be low.

Like nucleons Some states of unlike nucleons Like, unlike nucleon d force

A practical example

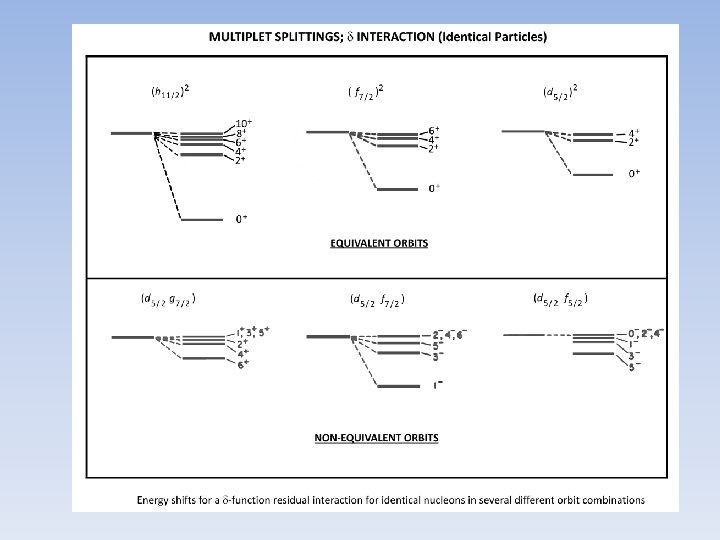
Data for identical orbits

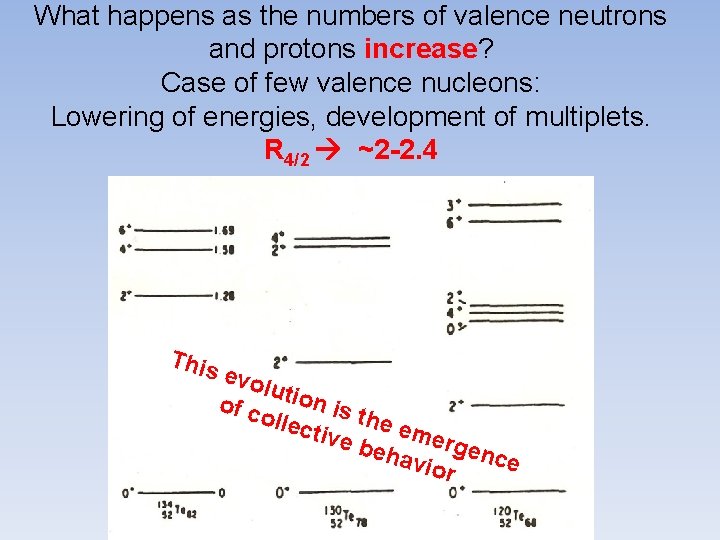
What happens as the numbers of valence neutrons and protons increase? Case of few valence nucleons: Lowering of energies, development of multiplets. R 4/2 ~2 -2. 4 This evo lutio n of c olle is the ctiv e e be merge nce hav ior

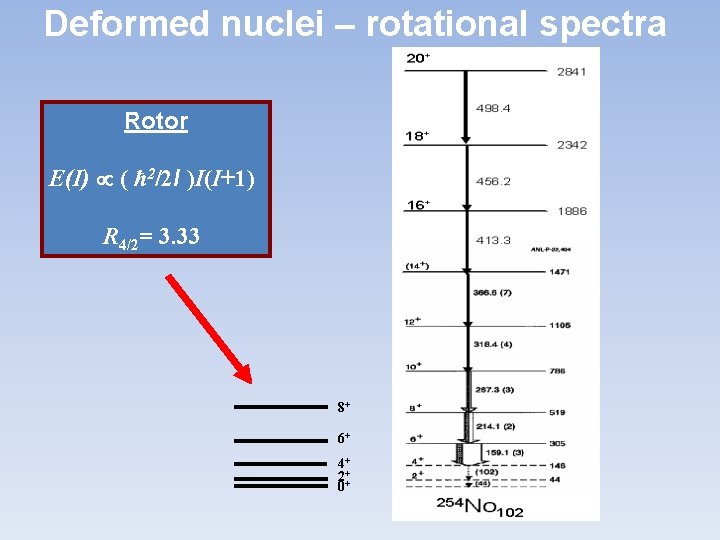
Lots of valence nucleons of both types: emergence of deformation and therefore rotation (nuclei live in the world, not in their own solipsistic enclaves) R 4/2 ~3. 33

Deformed nuclei – rotational spectra Rotor E(I) ( ħ 2/2 I )I(I+1) R 4/2= 3. 33 8+ 6+ 4+ 2++ 0

Think about the striking regularities in these data. Take a nucleus with A ~100 -200. The summed volume of all the nucleons is ~ 60 % the volume of the nucleus, and they orbit the nucleus ~ 1021 times per second! Instead of utter chaos, the result is very regular behavior, reflecting ordered, coherent, motions of these nucleons. This should astonish you. How can this happen? ? !!!! Much of understanding nuclei is understanding the relation between nucleonic motions and collective behavior

Competition between pairing and the p-n interactions A simple microscopic guide to the evolution of structure (The next slides allow you to estimate the structure of any nucleus by multiplying and dividing two numbers each less than 30) (or, if you prefer, you can get the same result from 10 hours of supercomputer time)

Valence Proton-Neutron Interactions Correlations, collectivity, deformation. Sensitive to magic numbers. Np Nn Scheme Highlight deviant nuclei

p-n / pairing P= Np Nn Np + N n Pairing int. ~ 1 Me. V, p–n pairing p-n interactions per pairing interaction p-n ~ 200 ke. V (later) Hence takes ~ 5 p-n int. to compete with one pairing int. P~5

Comparing with the data

Comparison with the data

Backups

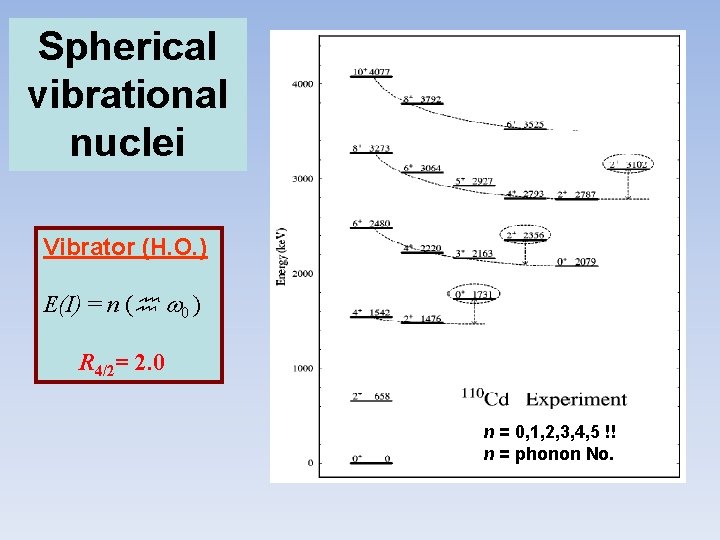
Spherical vibrational nuclei Vibrator (H. O. ) E(I) = n ( 0 ) R 4/2= 2. 0 n = 0, 1, 2, 3, 4, 5 !! n = phonon No.

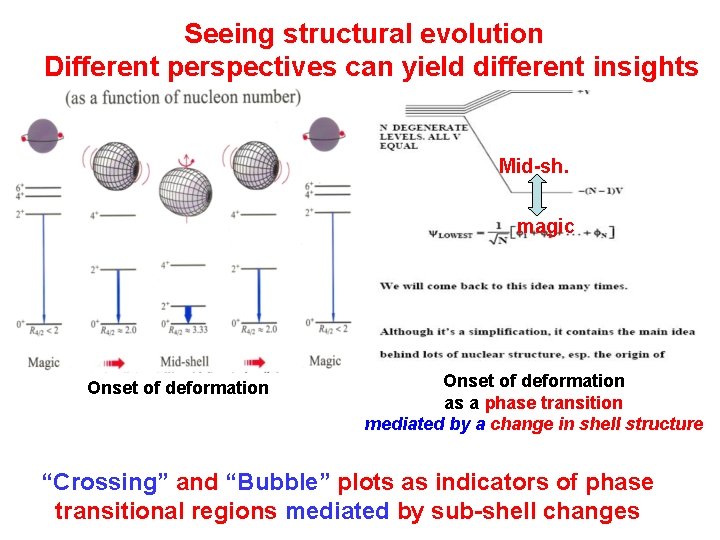
Seeing structural evolution Different perspectives can yield different insights Mid-sh. magic Onset of deformation as a phase transition mediated by a change in shell structure “Crossing” and “Bubble” plots as indicators of phase transitional regions mediated by sub-shell changes

Separation energies across the nuclear chart

Separate radial and angular coordinates