Proton Spin Puzzle 20 years later HaiYang Cheng

Proton Spin Puzzle: 20 years later Hai-Yang Cheng Academia Sinica, Taipei l Deep inelastic scattering l Proton spin puzzle l Theoretical progress CYCU, June 26, 2007

Non-relativistic SU(6) QM ⇒ proton spin comes from constitutent quark’s spin. U=4/3, D=-1/3, so that U+ D=1. However, this model predicts g. A=5/3, while g. A=1. 258 experimentally Relativistic QM ⇒ quark spin + orbital angular momentum = Q+ Lq ½(0. 65+0. 35) How to explore the proton’s spin content ? It can be studied in deep inelastic scattering (DIS) 2

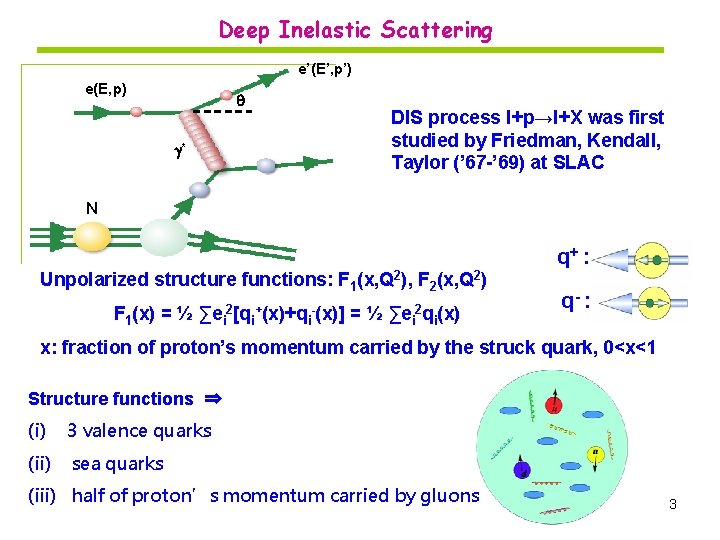
Deep Inelastic Scattering e(E, p) e’(E’, p’) k’ DIS process l+p→l+X was first studied by Friedman, Kendall, Taylor (’ 67 -’ 69) at SLAC * N Unpolarized structure functions: F 1(x, Q 2), F 2(x, Q 2) F 1(x) = ½ ∑ei 2[qi+(x)+qi-(x)] =½ ∑ei 2 qi(x) q+ : q- : x: fraction of proton’s momentum carried by the struck quark, 0<x<1 Structure functions ⇒ (i) 3 valence quarks (ii) sea quarks (iii) half of proton’s momentum carried by gluons 3

Polarized DIS Consider polarized DIS process: l +p →l+X and measure asymmetry g 1 p(x)= ½∑ei 2[qi+(x)-qi-(x)]= ½∑ei 2 qi(x) q(x, Q 2)= In general, q= qv+ qs. In absence of sea polarization 10 g 1 p(x)dx=½∑eq 2 q=½(4/9 uv+1/9 dv) neutron decay ⇒ uv- dv=1. 2695± 0. 0029 hyperon decay ⇒ uv + dv=0. 585± 0. 025 uv = 0. 93± 0. 02, dv = -0. 34± 0. 02, 10 g 1 p(x)dx 0. 18 first derived by Ellis & Jaffe in 1974 4

SLAC (’ 76, ’ 83) covers the range 0. 1<x<0. 7 10 g 1 p(x)dx = 0. 094± 0. 016 Extrapolation to the unmeasured x region⇒ 10 g 1 p(x)dx=0. 17± 0. 05, consistent with Ellis-Jaffe sum rule EMC (European Muon Collaboration, 87 -89), 0. 01<x<0. 7 at <Q 2>=10. 7 Ge. V 2 0. 70. 1 g 1 p(x)dx = 0. 090 ± 0. 015 0. 10. 01 g 1 p(x)dx = 0. 030 ± 0. 016 Hence, 10 g 1 p(x)dx = 0. 126 ± 0. 018 Lower than EJ sum rule expectation ⇒ importance of sea polarization 5

Solving the three equations for q u- d = 1. 2695± 0. 0029, u+ d-2 s = 0. 585± 0. 025 yields u = 0. 77± 0. 06, d = -0. 49± 0. 06, s = -0. 15± 0. 06 ∑≡ u+ d+ s = 0. 14± 0. 18 Two surprises: n strange sea polarization is sizable & negative n very little of the proton spin is carried by quarks ⇒ Proton Spin Crisis 6

The so-called “proton spin crisis” is not pertinent since the proton helicity content explored in the DIS experiment is, strictly speaking, defined in the infinite momentum frame in terms of QCD current quarks and gluons, whereas the spin structure of the proton in the proton rest frame is referred to the constituent quarks. …. . It is not sensible to compare apple with orange. What trigged by the EMC experiment is the “proton helicity decomposition puzzle” rather than the “proton spin crisis” HYC, hep-ph/0002157 q( momentum frame) q. QM(rest frame) 7

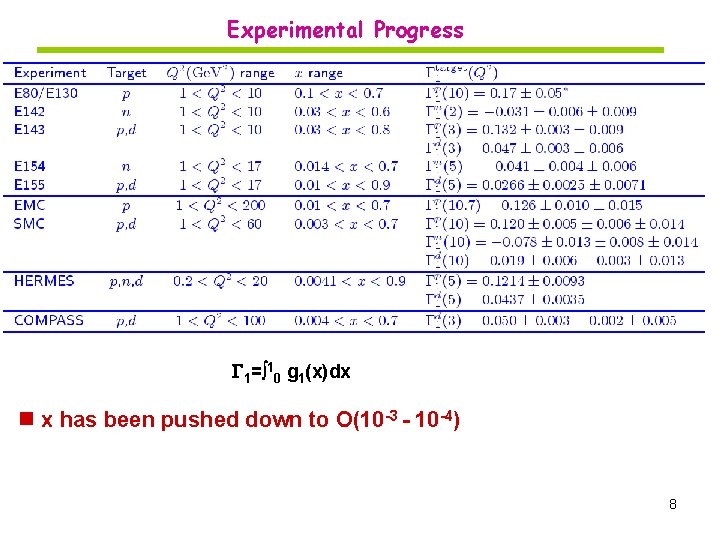
Experimental Progress 1= 10 g 1(x)dx n x has been pushed down to O(10 -3 - 10 -4) 8

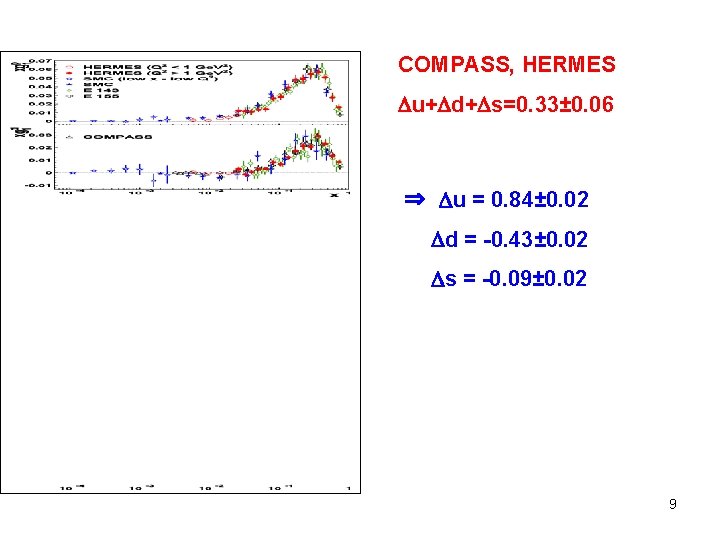
COMPASS, HERMES u+ d+ s=0. 33± 0. 06 ⇒ u = 0. 84± 0. 02 d = -0. 43± 0. 02 s = -0. 09± 0. 02 9

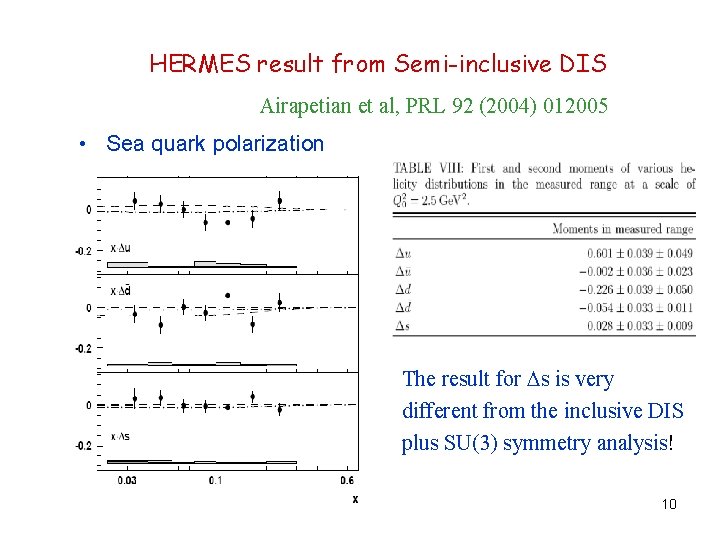
HERMES result from Semi-inclusive DIS Airapetian et al, PRL 92 (2004) 012005 • Sea quark polarization The result for s is very different from the inclusive DIS plus SU(3) symmetry analysis! 10

Anomalous gluon interpretation Consider QCD corrections to order s: Efremov, Teryaev; Altarelli, Ross; Carlitz, Collins, Muller (’ 88) from (a) from (b) Anomalous gluon contribution ( s/2 ) G arises from photon-gluon scattering. Since G(Q 2) ln. Q 2 and s(Q 2) (ln. Q 2)-1 ⇒ s(Q 2) G(Q 2) is conserved and doesn’t vanish in Q 2→ limit G(Q 2) is accumulated with increasing Q 2 Why is this QCD correction so special ? 11

QCD corrections imply that If G is positive and large enough, one can have s 0 and u+ d 0. 60 ⇒ proton spin problem is resolved provided that G (2 / s)(0. 09) 1. 7 ⇒ Lq+G also increases with ln. Q 2 with fine tuning This anomalous gluon interpretation became very popular after 1988 Historical remarks: 1. Photon-gluon box diagram was first computed by Kodaira (’ 80) 2. In 1982 Chi-Sing Lam & Bing-An Li obtained anomalous gluon contribution to 1 p and identify G with <N|K |N> 3. The same box diagram was also computed by Ratcliffe (’ 83) using dimensional regularization 12

Operator Product Expansion moments of structure function= 10 xn-1 F(x)dx = ∑ Cn(q)<p, s|On|p, s> =short-distance long-distance No twist-2, spin-1 gauge-invariant local gluonic operator first moment OPE ⇒ Gluons do not contribute to 1 p ! One needs sea quark polarization to account for experiment (Jaffe, Manohar ’ 89) n How to achieve s -0. 09 ? Sea polarization (for massless quarks) cannot be induced perturbatively from hard gluons (helicity conservation ⇒ s=0 for massless quarks) n J 5 has anomalous dimension at 2 -loop (Kodaira ’ 79) ⇒ q is Q 2 dependent, against intuition 13

A hot debate between anomalous gluon & sea quark interpretations before 1995 ! anomalous gluon sea quark Efremov, Teryaev Jaffe, Manohar Altarelli, Ross Bodwin, Qiu Carlitz, Collins, Muller Ellis, Karlinear Soffer, Perparata Bass, Thomas Strirling … Roberts Ball, Forte Gluck, Reya, Vogelsang Lampe Mankiewicz Gehrmann …. Anselmino, Efremov, Leader [Phys. Rep, 261, 1 (1995)] 14

Factorization scheme dependence n It was realized by Bodwin, Qiu (’ 90) and by Manohar (’ 90) that hard gluonic contribution to 1 p is a matter of convention used for defining q fact. scheme dependent Consider polarized photon-gluon cross section 1. Its hard part contributes to CG and soft part to qs. This decomposition depends on the choice of factorization scheme 2. It has an axial QCD anomaly that breaks down chiral symmetry Int. J. Mod. Phys. A 11, 5109 (1996) 15

n Photon-gluon box diagram is u. v. finite. CG is indep of choice of IR & collinear regulators, but depends on u. v. regulator of q/G(x)= q. G(x) n Polarized triangle diagram has axial anomaly ⇒ If u. v. cutoff respects gauge symmetry but breaks chiral symmetry ⇒ q. G 0 GI CI anomaly Axial anomaly resides at k 2→ q. G convolutes with G to become qs HYC(’ 95) Muller, Teryaev (’ 97) 16

Two extreme schemes of interest (HYC, ’ 95) n gauge-invariant (GI) scheme (or MS scheme) -- Axial anomaly is at soft part, i. e. q. G, which is non-vanishing due to chiral symmetry breaking and 10 CG(x)=0 (but G 0) -- Sea polarization is mainly induced by gluons via axial anomaly n chiral-invariant (CI) scheme (or “jet”, “parton-model”, “k. T cut-off’, “Adler-Bardeen” scheme) Axial anomaly is at hard part, i. e. CG, while qs induced by hard gluon vanishes u Hard gluonic contribution to g 1 p is matter of factorization convention used for defining q u It is necessary to specify the factorization scheme for data analysis 17

My conclusion: In retrospect, the dispute among the anomalous gluon and sea -quark explanations…before 1996 is considerably unfortunate and annoying since the fact that g 1 p(x) is independent of the definition of the quark spin density and hence the choice of the factorization scheme due to the axial-anomaly ambiguity is presumably well known to all the practitioners in the field, especially to those QCD experts working in the area. hep-ph/0002157 18

How to probe gluon polarization ? n DIS via scaling violation in g 1(x, Q 2) n photon or jet or heavy quark production in polarized pp collider, leptonproton collider or lepton-proton fixed target RHIC (at BNL): via direct high-p. T prompt , production 2 jet production HERMES (at DESY): via open charm production COMPASS (at CERN): via open charm production 19

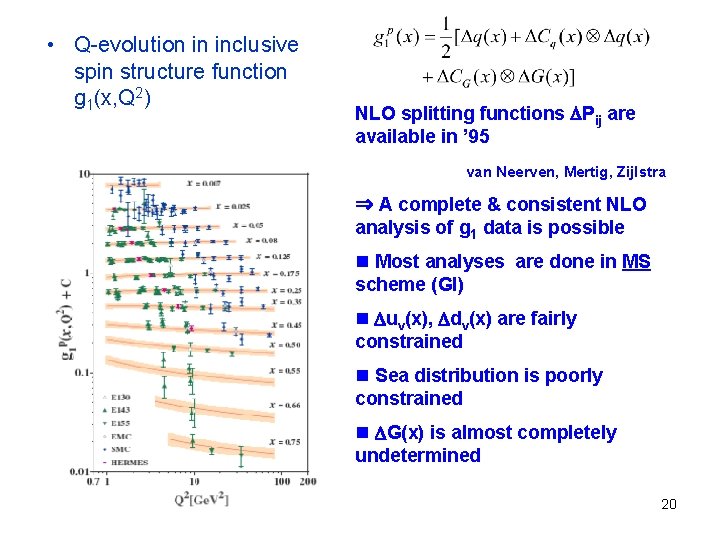
• Q-evolution in inclusive spin structure function g 1(x, Q 2) NLO splitting functions Pij are available in ’ 95 van Neerven, Mertig, Zijlstra ⇒ A complete & consistent NLO analysis of g 1 data is possible n Most analyses are done in MS scheme (GI) n uv(x), dv(x) are fairly constrained n Sea distribution is poorly constrained n G(x) is almost completely undetermined 20

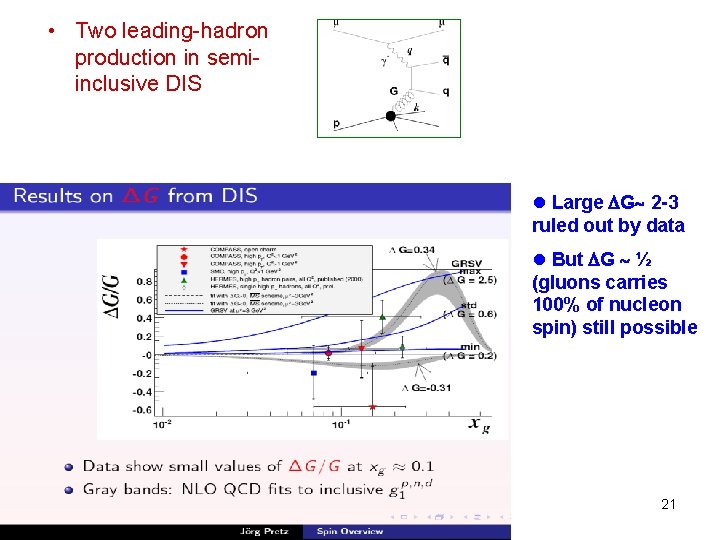
• Two leading-hadron production in semiinclusive DIS l Large G 2 -3 ruled out by data l But G ½ (gluons carries 100% of nucleon spin) still possible 21

RHIC: The First Polarised pp Collider 22

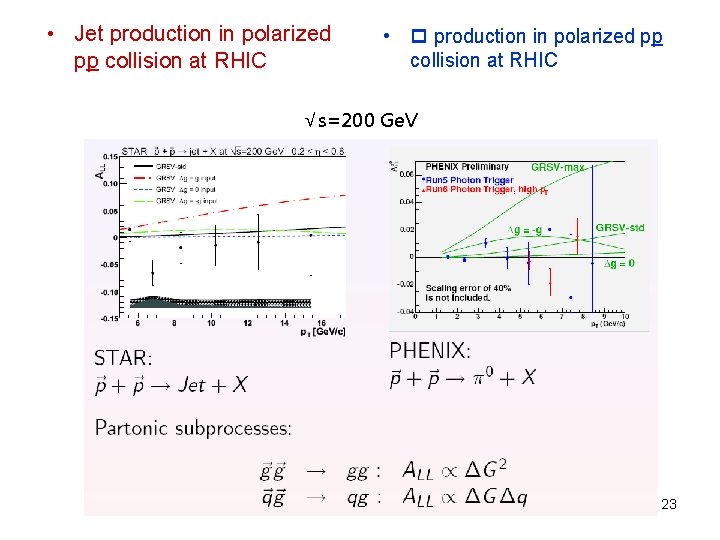
• Jet production in polarized pp collision at RHIC • production in polarized pp collision at RHIC √s=200 Ge. V 23

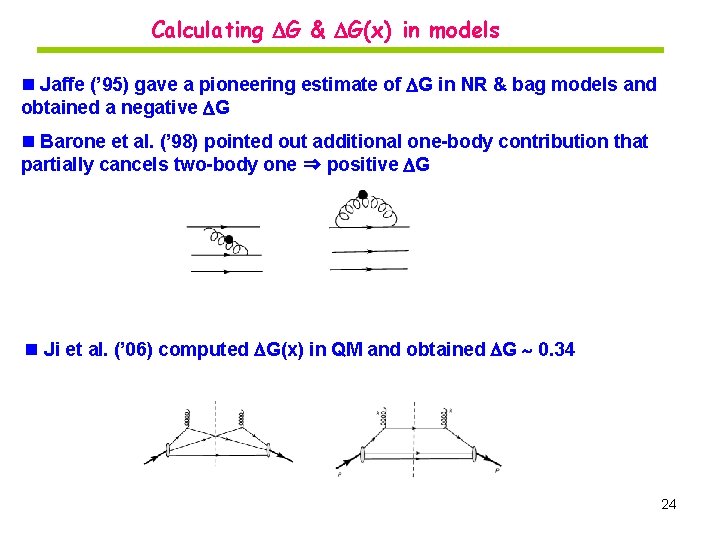
Calculating G & G(x) in models n Jaffe (’ 95) gave a pioneering estimate of G in NR & bag models and obtained a negative G n Barone et al. (’ 98) pointed out additional one-body contribution that partially cancels two-body one ⇒ positive G n Ji et al. (’ 06) computed G(x) in QM and obtained G 0. 34 24

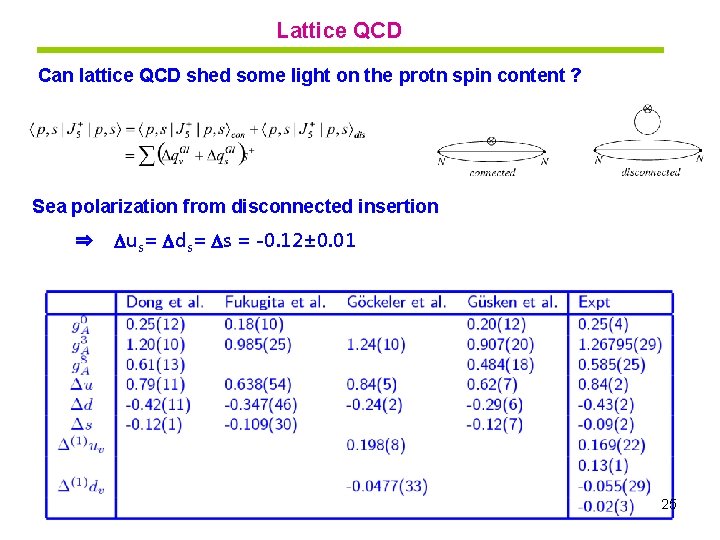
Lattice QCD Can lattice QCD shed some light on the protn spin content ? Sea polarization from disconnected insertion ⇒ us= ds= s = -0. 12± 0. 01 25

Orbital angular momentum can be inferred from lattice result for Jq=0. 30± 0. 07 (Mathur et al. 2000) ⇒ Lq 0. 10± 0. 06 for ∑ 0. 25 At Q 2→ , Ji, Tang & Hoodbhoy found (’ 96) for nf=6 Analogous to the nucleon’s momentum partition: half of the proton’s momentum is carried by gluons 26

Conclusions What do we learn in past 20 years about the proton helicity decomposition ? n ∑ & Lq are factorization scheme dependent, but not Jq DIS data ⇒ ∑GI 0. 30, s. GI -0. 08 G(x) & qs(x) are weakly constrained n SIDIS & RHIC data imply a small G n At Q 2→ , Jq=0. 26, JG=0. 24 Lattice QCD ⇒ Jq=0. 30 ± 0. 07 27