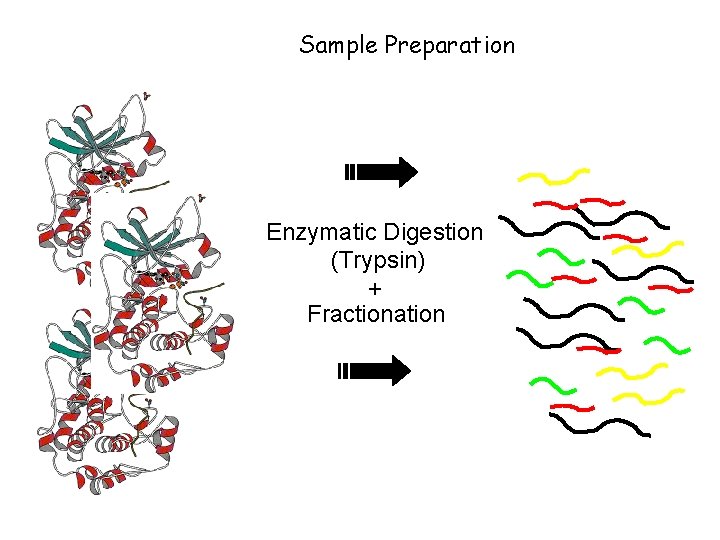
Protein sequencing and Mass Spectrometry Sample Preparation Enzymatic

Protein sequencing and Mass Spectrometry

Sample Preparation Enzymatic Digestion (Trypsin) + Fractionation

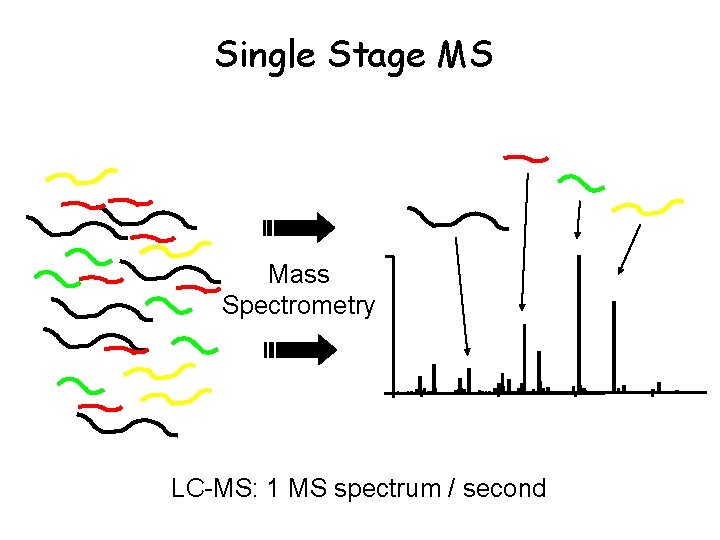
Single Stage MS Mass Spectrometry LC-MS: 1 MS spectrum / second

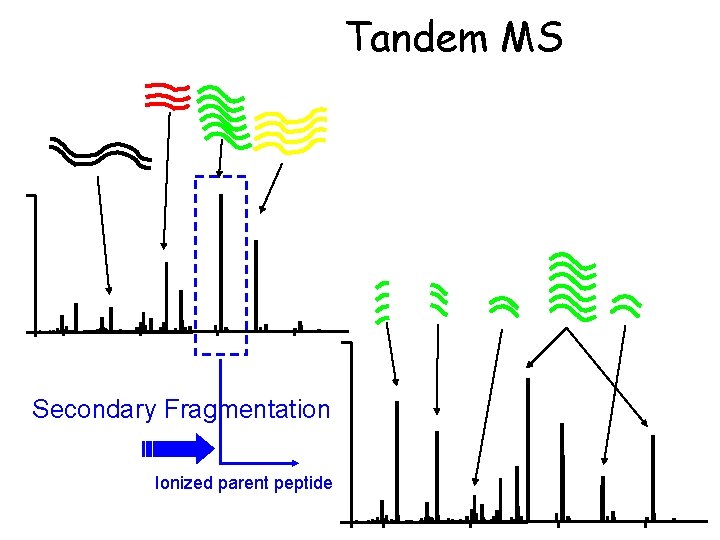
Tandem MS Secondary Fragmentation Ionized parent peptide

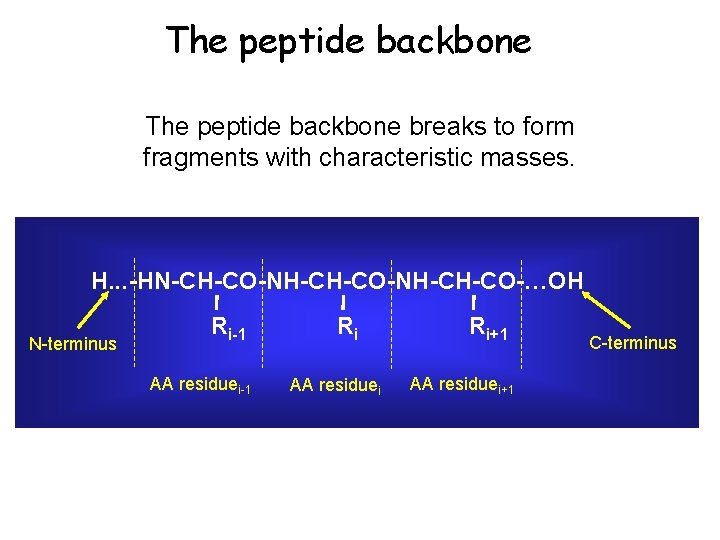
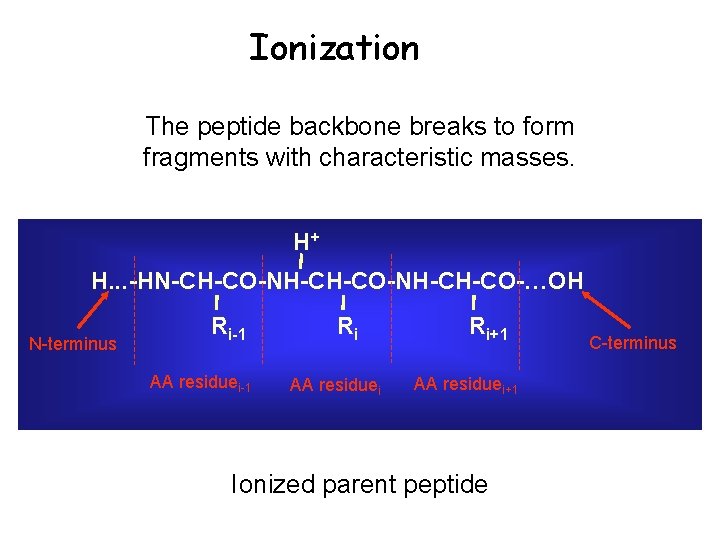
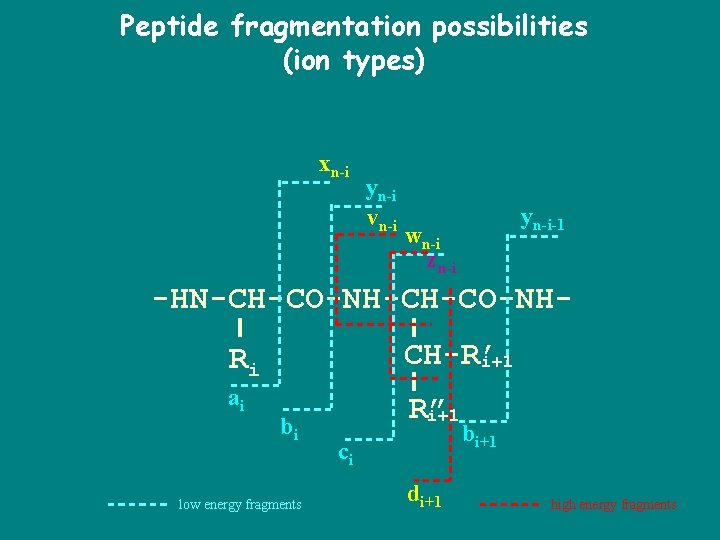
The peptide backbone breaks to form fragments with characteristic masses. H. . . -HN-CH-CO-NH-CH-CO-…OH N-terminus Ri-1 AA residuei-1 Ri AA residuei Ri+1 AA residuei+1 C-terminus

Ionization The peptide backbone breaks to form fragments with characteristic masses. H+ H. . . -HN-CH-CO-NH-CH-CO-…OH N-terminus Ri-1 AA residuei-1 Ri AA residuei Ri+1 AA residuei+1 Ionized parent peptide C-terminus

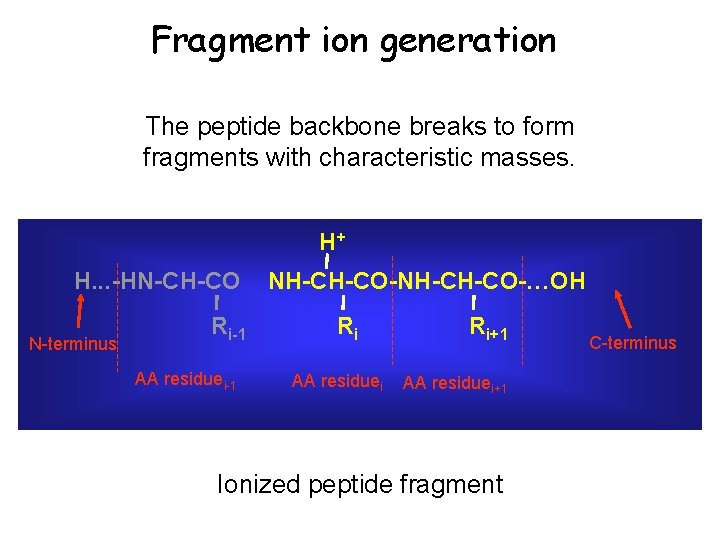
Fragment ion generation The peptide backbone breaks to form fragments with characteristic masses. H+ H. . . -HN-CH-CO N-terminus Ri-1 AA residuei-1 NH-CH-CO-…OH Ri AA residuei Ri+1 AA residuei+1 Ionized peptide fragment C-terminus

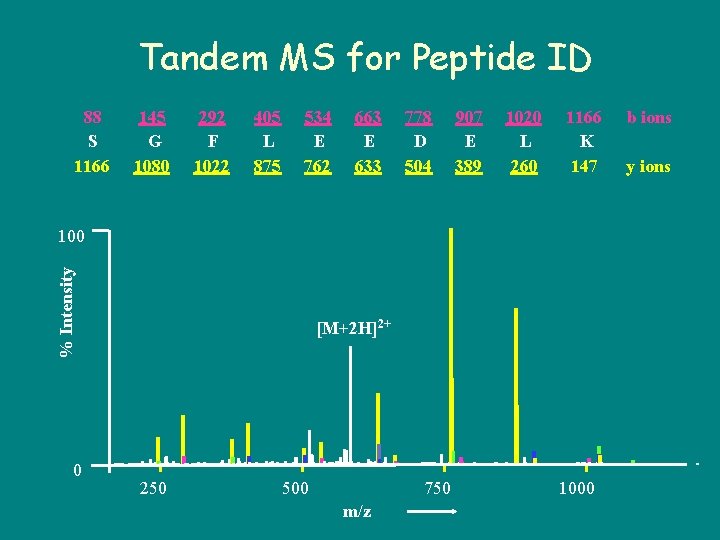
Tandem MS for Peptide ID 88 S 1166 145 G 1080 292 F 1022 405 L 875 534 E 762 663 E 633 778 D 504 907 E 389 1020 L 260 1166 K 147 % Intensity 100 0 [M+2 H]2+ 250 500 750 m/z 1000 b ions y ions

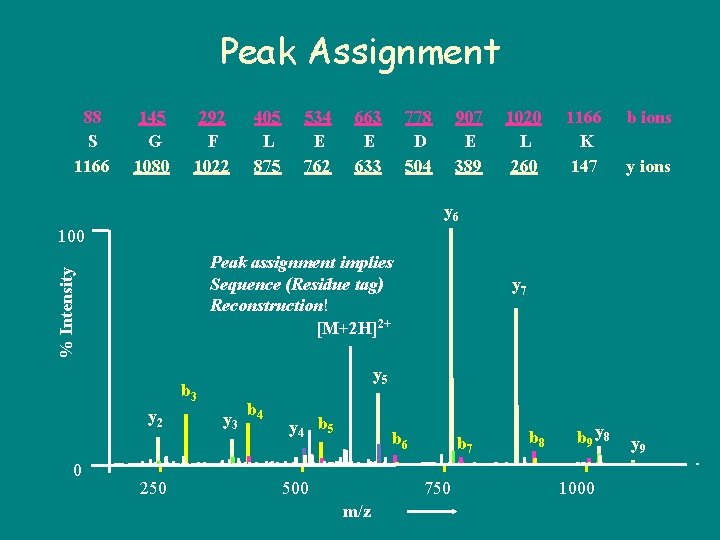
Peak Assignment 88 S 1166 145 G 1080 292 F 1022 405 L 875 534 E 762 663 E 633 778 D 504 907 E 389 1020 L 260 1166 K 147 b ions y 6 100 % Intensity Peak assignment implies Sequence (Residue tag) Reconstruction! [M+2 H]2+ y 5 b 3 y 2 0 250 y 7 y 3 b 4 y 4 b 5 b 6 500 b 7 750 m/z b 8 b 9 y 8 1000 y 9

Database Searching for peptide ID • For every peptide from a database – Generate a hypothetical spectrum – Compute a correlation between observed and experimental spectra – Choose the best • Database searching is very powerful and is the de facto standard for MS. – Sequest, Mascot, and many others

Spectra: the real story • Noise Peaks • Ions, not prefixes & suffixes • Mass to charge ratio, and not mass – Multiply charged ions • Isotope patterns, not single peaks

Peptide fragmentation possibilities (ion types) xn-i yn-i vn-i yn-i-1 wn-i zn-i -HN-CH-CO-NHRi CH-R’ i+1 ai R” i+1 bi low energy fragments ci di+1 bi+1 high energy fragments

Ion types, and offsets • • • P = prefix residue mass S = Suffix residue mass b-ions = P+1 y-ions = S+19 a-ions = P-27

Mass-Charge ratio • The X-axis is (M+Z)/Z – Z=1 implies that peak is at M+1 – Z=2 implies that peak is at (M+2)/2 • M=1000, Z=2, peak position is at 501 – Suppose you see a peak at 501. Is the mass 500, or is it 1000?

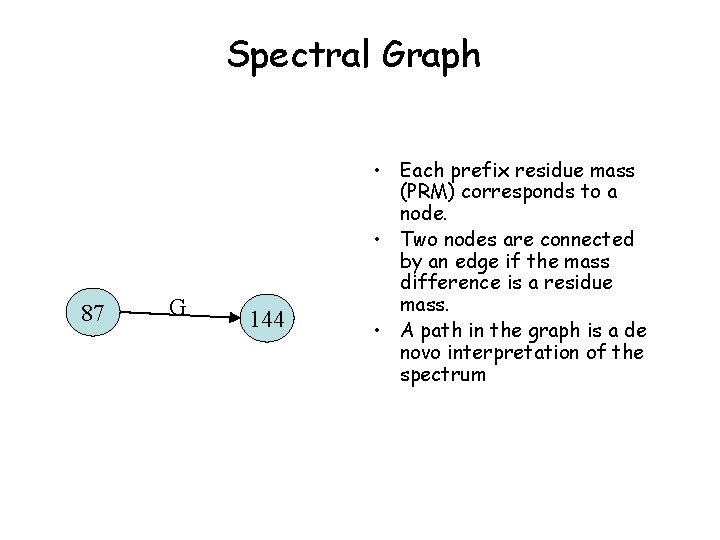
Spectral Graph 87 G 144 • Each prefix residue mass (PRM) corresponds to a node. • Two nodes are connected by an edge if the mass difference is a residue mass. • A path in the graph is a de novo interpretation of the spectrum

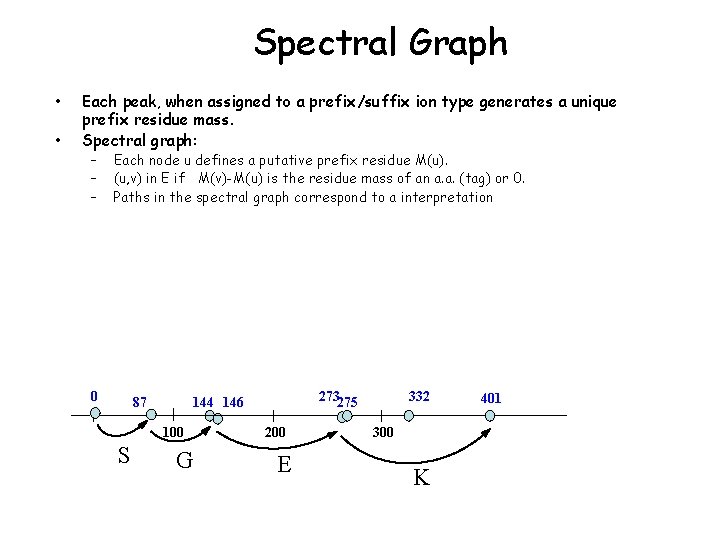
Spectral Graph • • Each peak, when assigned to a prefix/suffix ion type generates a unique prefix residue mass. Spectral graph: – – – Each node u defines a putative prefix residue M(u). (u, v) in E if M(v)-M(u) is the residue mass of an a. a. (tag) or 0. Paths in the spectral graph correspond to a interpretation 0 87 100 S 273275 144 146 G 200 E 332 300 K 401

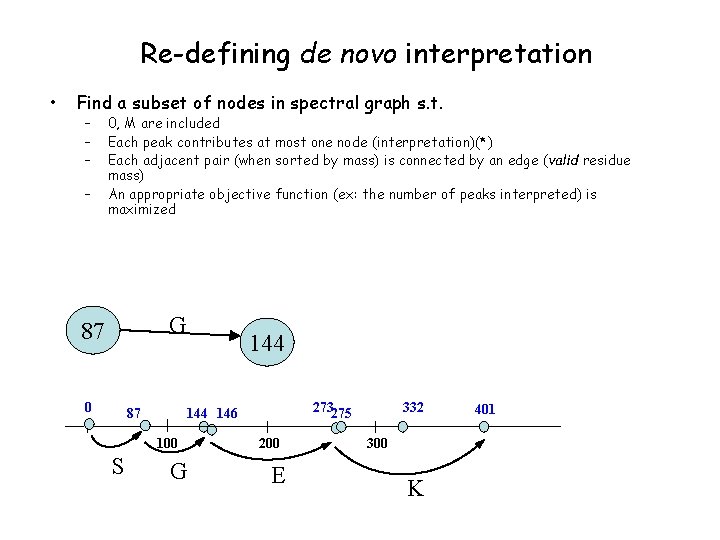
Re-defining de novo interpretation • Find a subset of nodes in spectral graph s. t. – – 0, M are included Each peak contributes at most one node (interpretation)(*) Each adjacent pair (when sorted by mass) is connected by an edge (valid residue mass) An appropriate objective function (ex: the number of peaks interpreted) is maximized G 87 0 87 273275 144 146 100 S 144 G 200 E 332 300 K 401

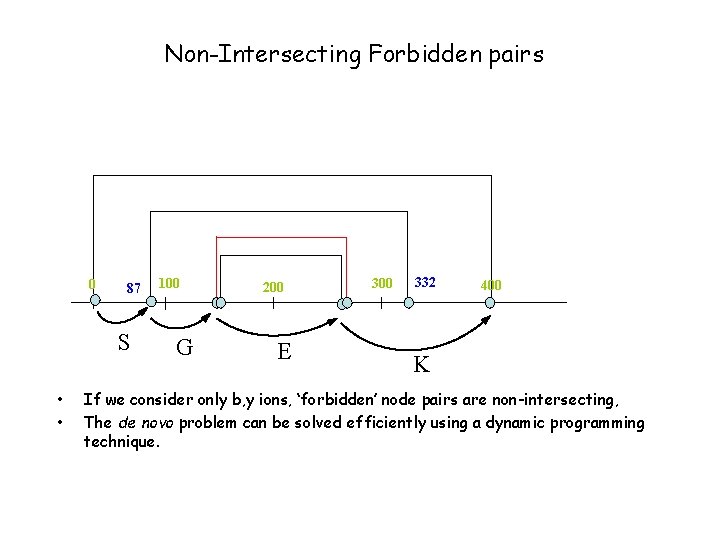
Two problems • Too many nodes. – Only a small fraction are correspond to b/y ions (leading to true PRMs) (learning problem) – Even if the b/y ions were correctly predicted, each peak generates multiple possibilities, only one of which is correct. We need to find a path that uses each peak only once (algorithmic problem). – In general, the forbidden pairs problem is NP-hard 0 87 100 S 273275 144 146 G 200 E 332 300 K 401

However, . . • The b, y ions have a special non-interleaving property • Consider pairs (b 1, y 1), (b 2, y 2) – If (b 1 < b 2), then y 1 > y 2

Non-Intersecting Forbidden pairs 0 87 S • • 100 G 200 E 300 332 400 K If we consider only b, y ions, ‘forbidden’ node pairs are non-intersecting, The de novo problem can be solved efficiently using a dynamic programming technique.

The forbidden pairs method • There may be many paths that avoid forbidden pairs. • We choose a path that maximizes an objective function, – EX: the number of peaks interpreted

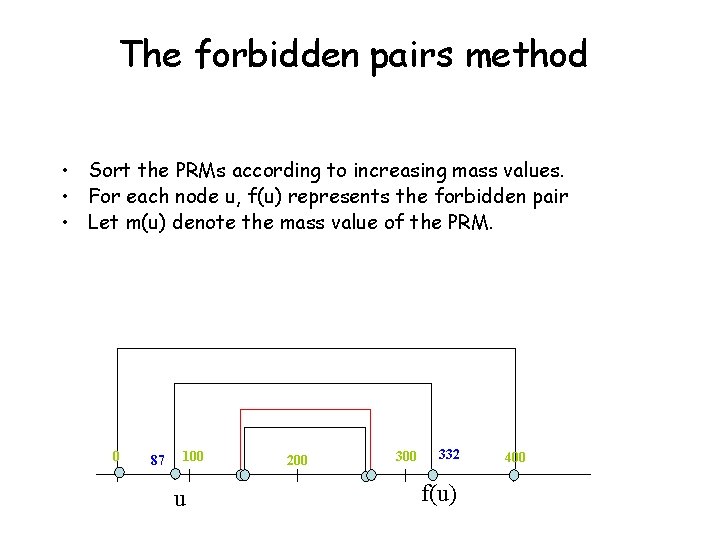
The forbidden pairs method • Sort the PRMs according to increasing mass values. • For each node u, f(u) represents the forbidden pair • Let m(u) denote the mass value of the PRM. 0 87 100 u 200 332 f(u) 400

D. P. forbidden pairs • Consider all pairs u, v – m[u] <= M/2, m[v] >M/2 • Define S(u, v) as the best score of a forbidden pair path from 0>u, v->M • Is it sufficient to compute S(u, v) for all u, v? 0 87 100 u 200 332 400 v

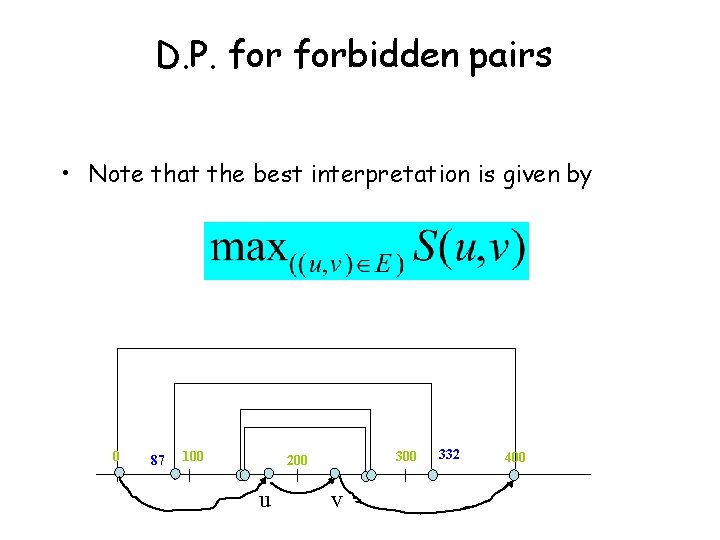
D. P. forbidden pairs • Note that the best interpretation is given by 0 87 100 300 200 u v 332 400

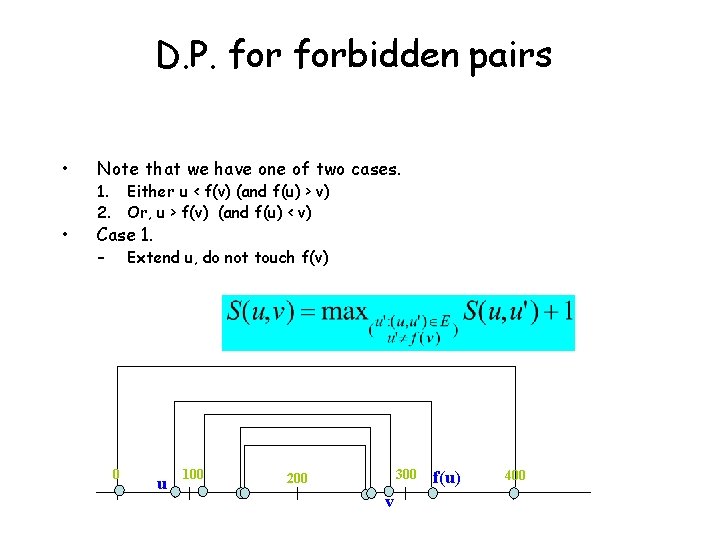
D. P. forbidden pairs • Note that we have one of two cases. • Case 1. Either u < f(v) (and f(u) > v) 2. Or, u > f(v) (and f(u) < v) – Extend u, do not touch f(v) 0 u 100 300 200 v f(u) 400

The complete algorithm for all u /*increasing mass values from 0 to M/2 */ for all v /*decreasing mass values from M to M/2 */ if (u > f[v]) else if (u < f[v]) If (u, v) E /*max. I is the score of the best interpretation*/ max. I = max {max. I, S[u, v]}