PROTEIN PHYSICS LECTURE 21 Protein Structures Kinetic Aspects

PROTEIN PHYSICS LECTURE 21 Protein Structures: Kinetic Aspects (3) · Nucleation in the 1 -st order phase transitions · Nucleation of protein folding · Solution of Levinthal paradox · Folding rate: chain length and 3 D fold (“contact order”)

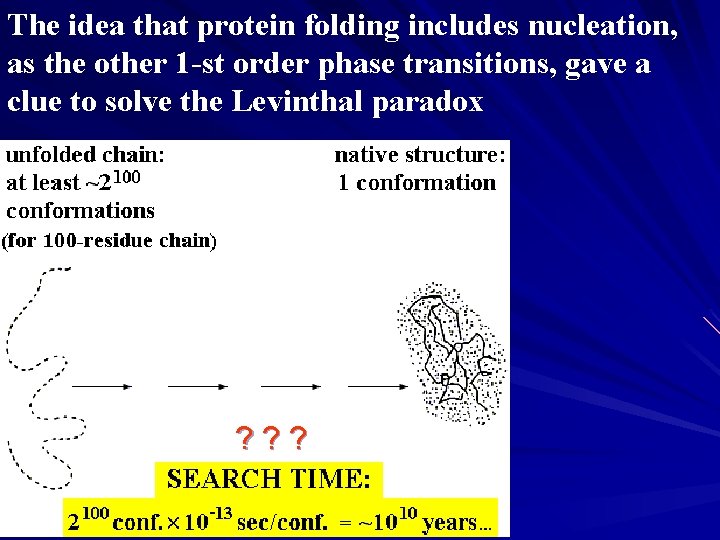
Levinthal paradox Native protein structure reversibly refolds from various starts, i. e. , it is thermodynamically stable. ? But how can protein chain find this unique structure - within seconds - among zillions alternatives? However, the same problem – how to find one configuration among zillions – is met by crystallization and other 1 -st order phase transitions.

1 -st order phase transition: rate of nucleation

The idea that protein folding includes nucleation, as the other 1 -st order phase transitions, gave a clue to solve the Levinthal paradox ? ? ?

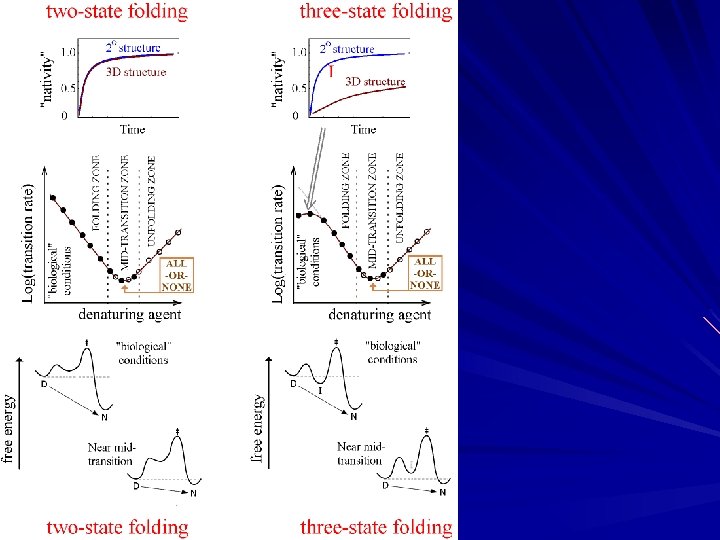
Before considering kinetics, let us recall basic facts on protein thermodynamics (for 1 -domain proteins, of 50– 200 residues). 1) Protein unfolding is reversible, and it occurs as an “all-ornone” transition in single-domain proteins. This means that only two states, native and denatured, are present (close to the mid-transition) in a visible quantity. 2) “All-or-none” transition requires the amino acid sequence that provides a large energy gap between the most stable structure and the bulk of misfolded ones. 3) The denatured state is often the random coil. 4) Native structure, even under physiological conditions, is only by a few kcal/mol more stable than the unfolded state (i. e. , it is not far from the mid-transition).

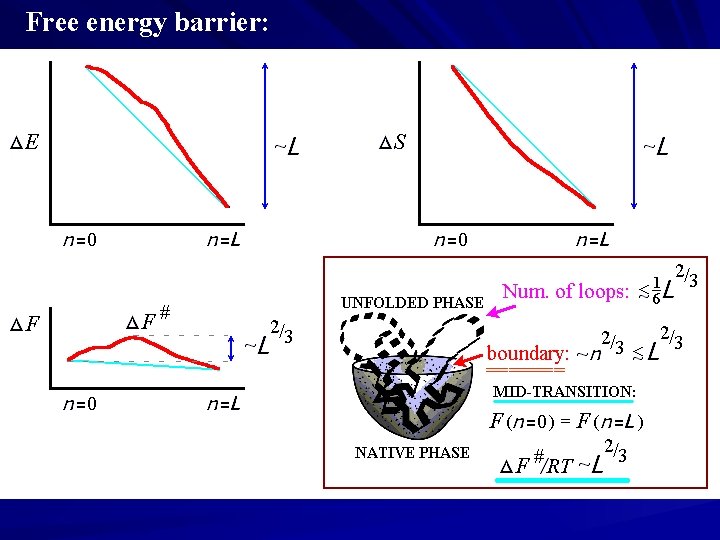
Let us consider sequential folding (or unfolding) of a chain that has a large energy gap between the most stable fold and the bulk of the other ones; and let us consider its folding close to thermodynamic mid-transition sequential folding/unfolding The same pathway: “detailed balance” How fast the most stable fold will be achieved? Note. Elementary rearrangement of 1 residue takes 1 -10 ns. Thus, 100 -residue protein would fold within ms, if there were no free energy barrier at the pathway…

Free energy barrier: =======

↓ Mid-transition THIS EXPLAINS PROTEIN FOLDING TIMES: ↓

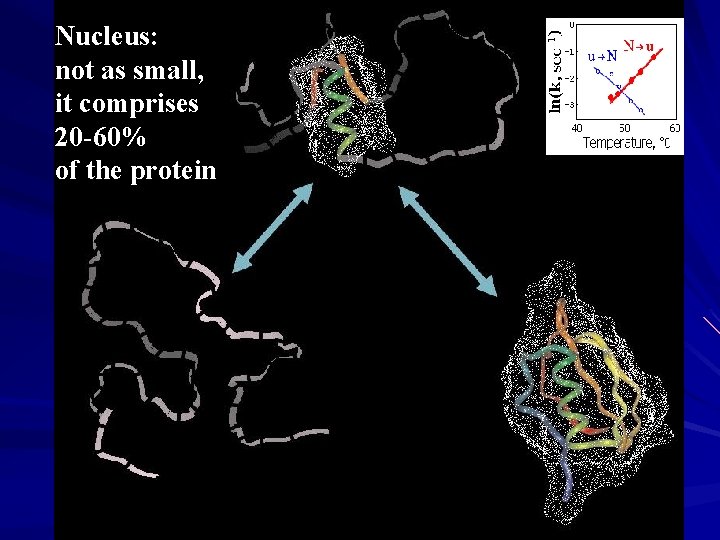
Nucleus: not as small, it comprises 20 -60% of the protein

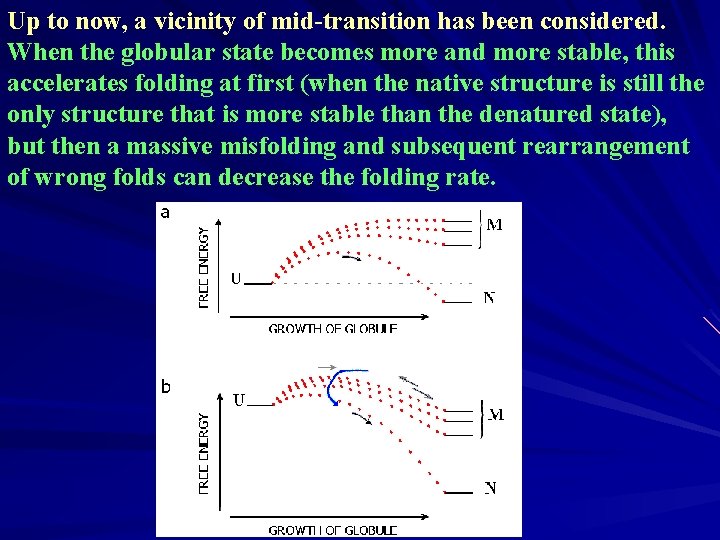
Up to now, a vicinity of mid-transition has been considered. When the globular state becomes more and more stable, this accelerates folding at first (when the native structure is still the only structure that is more stable than the denatured state), but then a massive misfolding and subsequent rearrangement of wrong folds can decrease the folding rate.

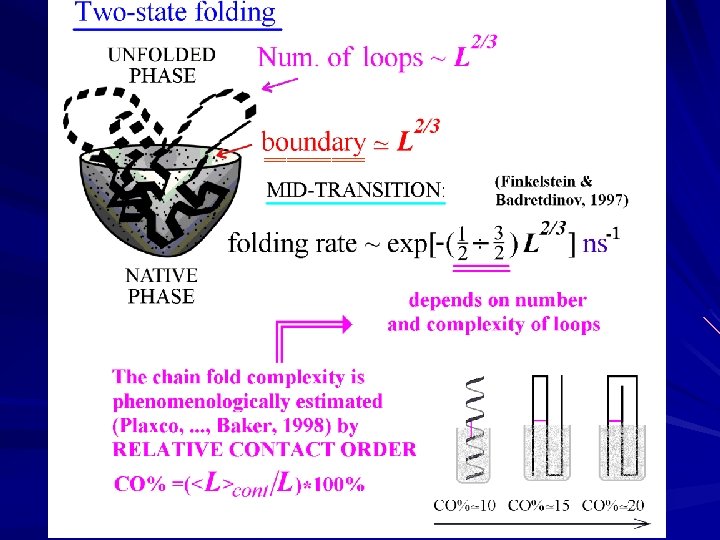
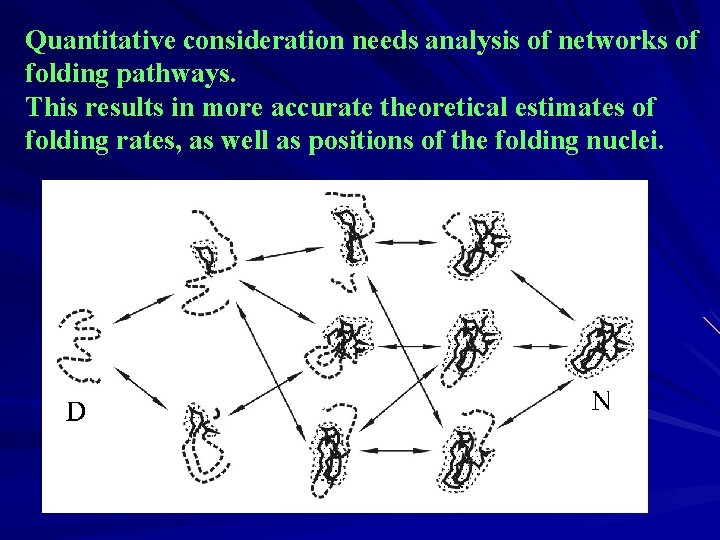
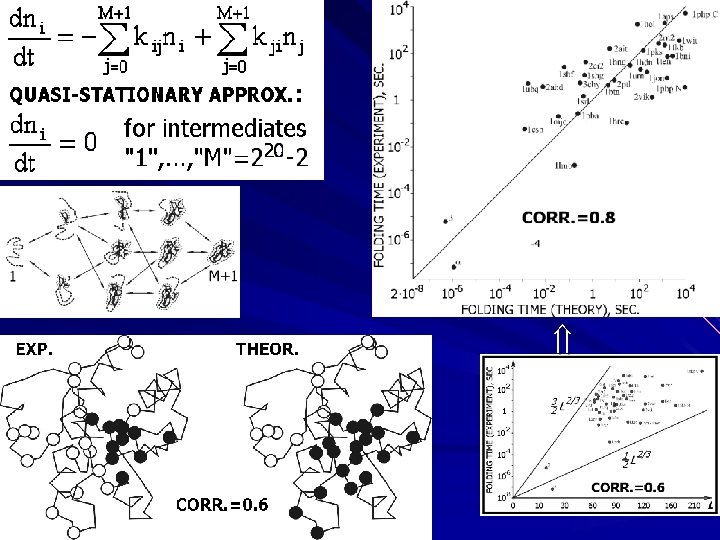
Quantitative consideration needs analysis of networks of folding pathways. This results in more accurate theoretical estimates of folding rates, as well as positions of the folding nuclei.

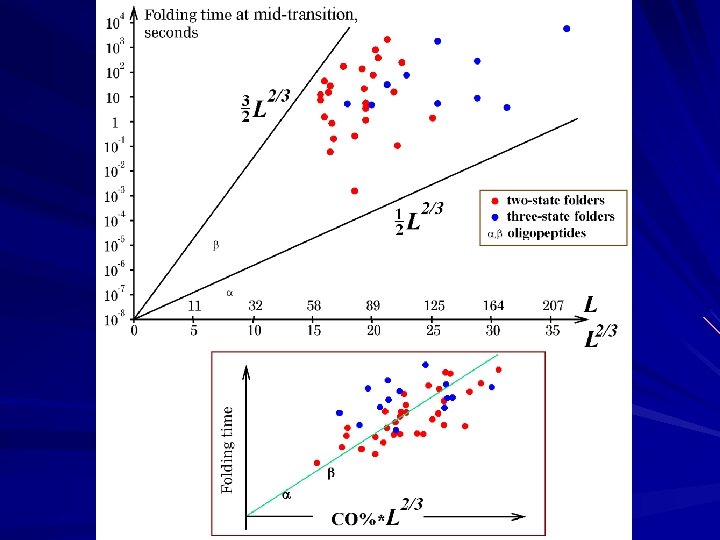
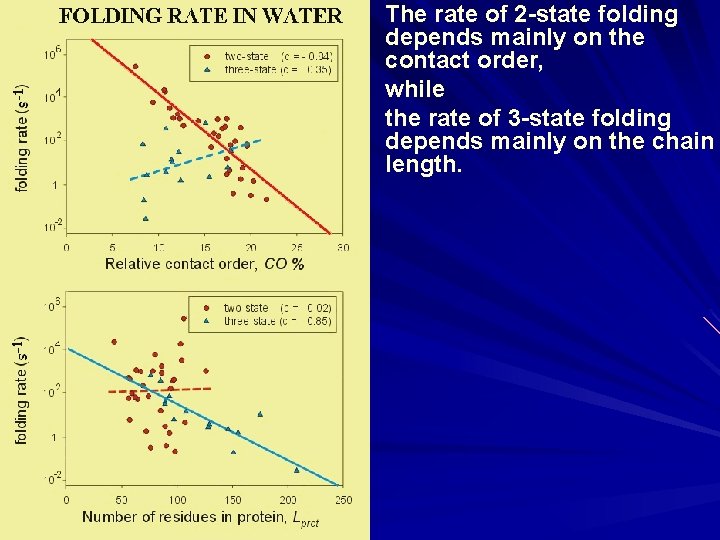
The rate of 2 -state folding depends mainly on the contact order, while the rate of 3 -state folding depends mainly on the chain length.

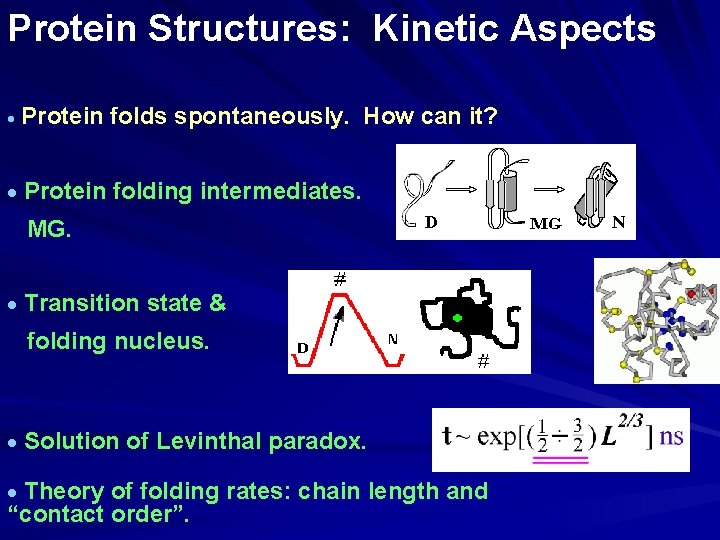
Protein Structures: Kinetic Aspects · Protein folds spontaneously. How can it? · Protein folding intermediates. MG. · Transition state & folding nucleus. · Solution of Levinthal paradox. · Theory of folding rates: chain length and “contact order”.