Proprits de Logarithmes Puisque une fonction logarithmique est

Propriétés de Logarithmes

Puisque une fonction logarithmique est la réciproque d’une fonction exponentielle, les deux s’éliminent… Souviens-toi: Alors: et =5 =7

Propriétés de Logarithmes COMPOSÉ = 1. = 2. = 3. = DÉCOMPOSÉ (ces propriétés suivent les règles d’exposants puisque logs = exposants)

Utilise des propriétés de logarithmes pour réécrire les expressions comme une somme ou une différence. Premièrement il faut réécrire des radicaux en forme de puissances rationnelles. Selon la deuxième propriété: Selon la première propriètè: Selon la troisième propriété:

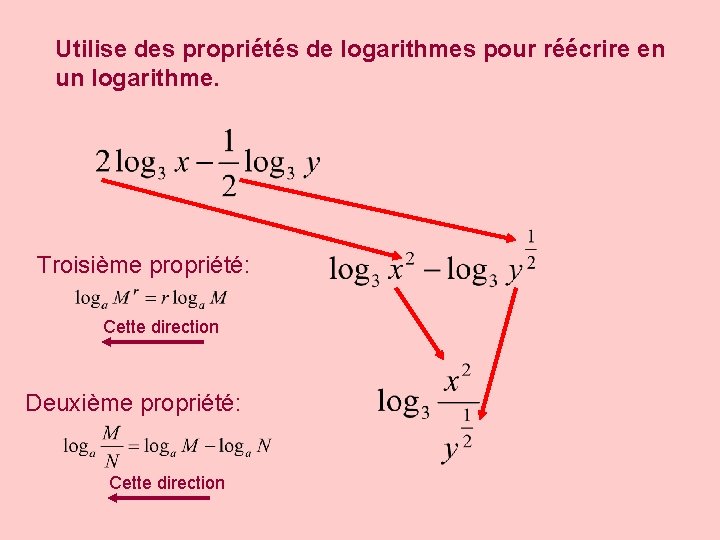
Utilise des propriétés de logarithmes pour réécrire en un logarithme. Troisième propriété: Cette direction Deuxième propriété: Cette direction

Encore… On peut prendre le logarithme de deux côtés d’une équation sans affecter la vérité de l’équation. L’inverse de la propriété au dessus

Forme exponentielle. (2 à la puissance de 3 est 8) Réécrire en forme logarithmique (2 à la quoi est 16? ) (2 à la quoi est 10? ) Pour vérifier essaie 23. 32 dans ta calculatrice (ça va être arrondi)) 3 e propriété Pour trouver x on divise par log 2 La calculatrice donne:

En général: Formule du Changement-de-Base “log commun” (à base 10) LOG LN Log “naturel” base e

Utilise la formule de changement de base De la calculatrice

Acknowledgement I wish to thank Shawna Haider from Salt Lake Community College, Utah USA for her hard work in creating this Power. Point. www. slcc. edu Shawna has kindly given permission for this resource to be downloaded from www. mathxtc. com and for it to be modified to suit the Western Australian and Canadian Mathematics Curricula. Stephen Corcoran Head of Mathematics St Stephen’s School – Carramar www. ststephens. wa. edu. au Translation: Mme J. Mc. Connell Head of Mathematics Calgary French & International School www. cfis. com