PROPRIEDADES Propriedade da mediatriz O que mediatriz o

PROPRIEDADES

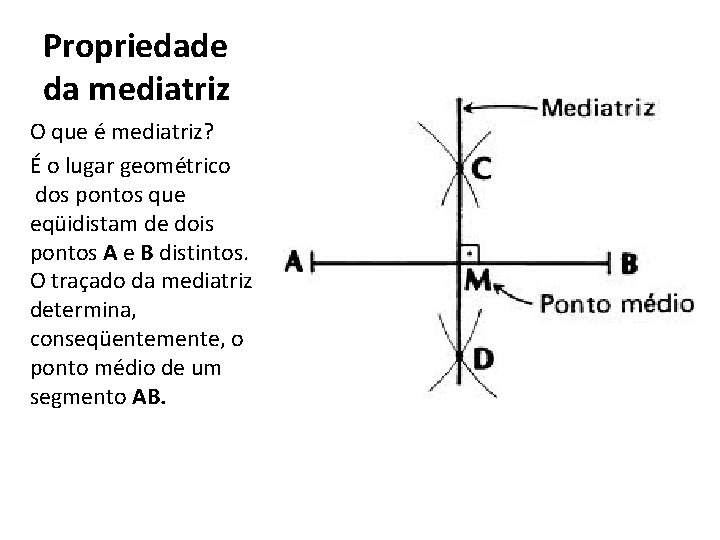
Propriedade da mediatriz O que é mediatriz? É o lugar geométrico dos pontos que eqüidistam de dois pontos A e B distintos. O traçado da mediatriz determina, conseqüentemente, o ponto médio de um segmento AB.

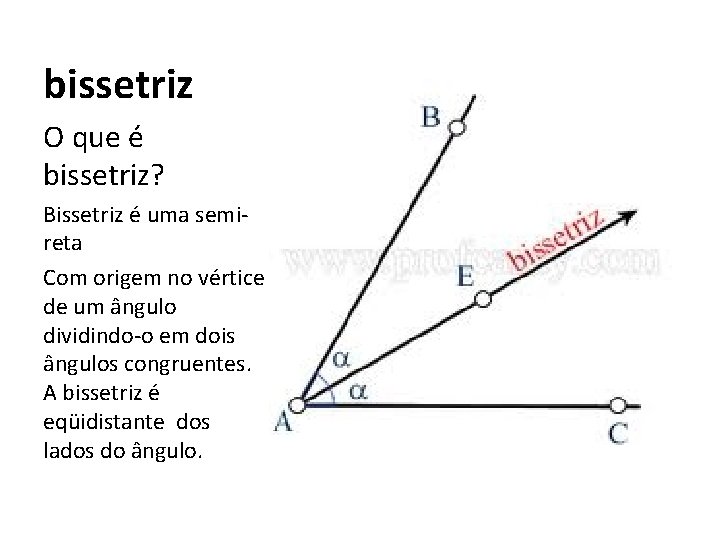
bissetriz O que é bissetriz? Bissetriz é uma semireta Com origem no vértice de um ângulo dividindo-o em dois ângulos congruentes. A bissetriz é eqüidistante dos lados do ângulo.

Existem dois tipos de bissetriz: • A bissetriz interna - que é a bissetriz do próprio ângulo • A bissetriz externa - é a bissetriz do ângulo suplementar a este. • Propriedades de uma bissetriz: • As bissetrizes de dois ângulos opostos pelo vértice são semi-reptais opostas. • Analogamente, as bissetrizes de dois ângulos replementares, são semi-retas opostas. • As bissetrizes de dois ângulos suplementares são perpendiculares.

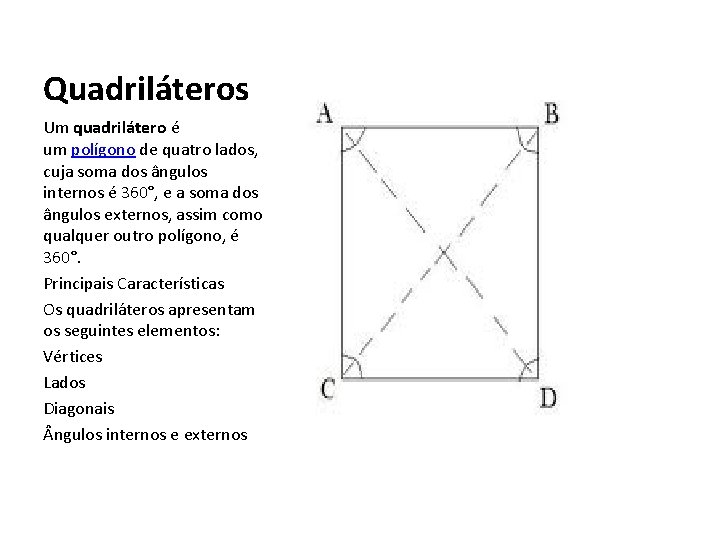
Quadriláteros Um quadrilátero é um polígono de quatro lados, cuja soma dos ângulos internos é 360°, e a soma dos ângulos externos, assim como qualquer outro polígono, é 360°. Principais Características Os quadriláteros apresentam os seguintes elementos: Vértices Lados Diagonais ngulos internos e externos

Quadriláteros • Na geometria, cada figura regular está associada a uma expressão matemática capaz de determinar a medida de sua superfície. Mas em alguns casos, a determinação da área deve ser calculada utilizando duas ou mais expressões. Esse tipo de cálculo exige uma interpretação espacial da figura, diagnosticando o tipo de expressão que será usado no cálculo da área.

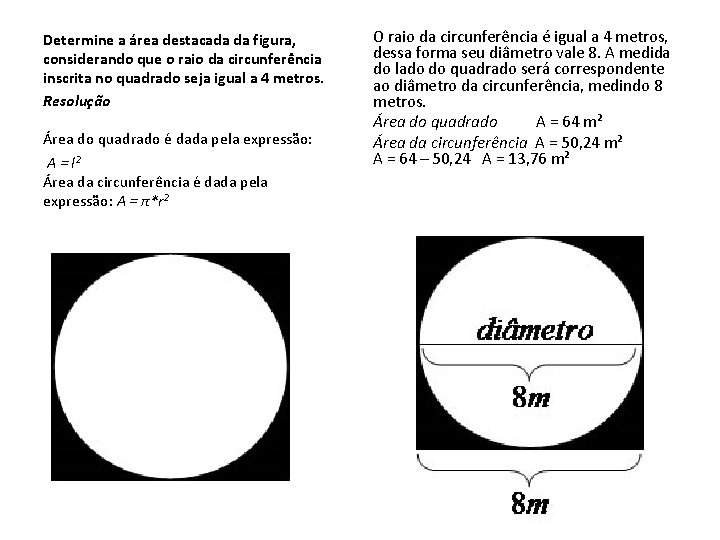
Determine a área destacada da figura, considerando que o raio da circunferência inscrita no quadrado seja igual a 4 metros. Resolução Área do quadrado é dada pela expressão: A = l² Área da circunferência é dada pela expressão: A = π*r² O raio da circunferência é igual a 4 metros, dessa forma seu diâmetro vale 8. A medida do lado do quadrado será correspondente ao diâmetro da circunferência, medindo 8 metros. Área do quadrado A = 64 m² Área da circunferência A = 50, 24 m² A = 64 – 50, 24 A = 13, 76 m²

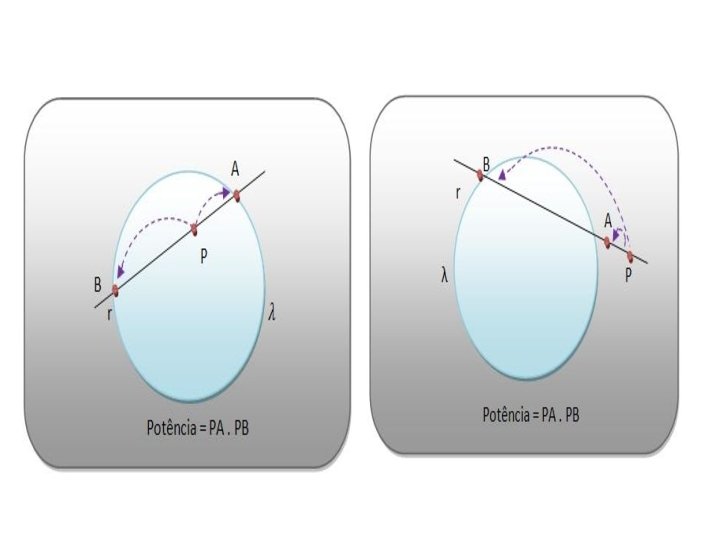
Potencia de ponto • Potência de um ponto em relação a uma circunferência. Considerando um ponto P e uma circunferência λ, dizemos que uma reta r passa por P e interrompe λ tanto no ponto A, como no ponto B. O produto das medidas dos segmentos PA e PB nada mais são do que a potência do ponto P em ralação a λ.

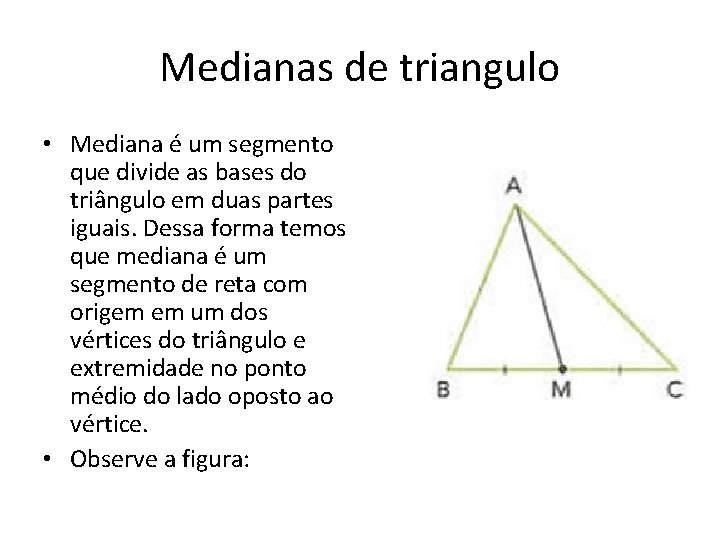
Medianas de triangulo • Mediana é um segmento que divide as bases do triângulo em duas partes iguais. Dessa forma temos que mediana é um segmento de reta com origem em um dos vértices do triângulo e extremidade no ponto médio do lado oposto ao vértice. • Observe a figura:

• A, B e C são os vértices do ΔABC. M ponto médio da base BC, dessa forma • BM = MC. • AM segmento de reta com extremidades no vértice A e no ponto médio M, portanto, nesse exemplo podemos dizer que o segmento AM é a mediana do ΔABC.

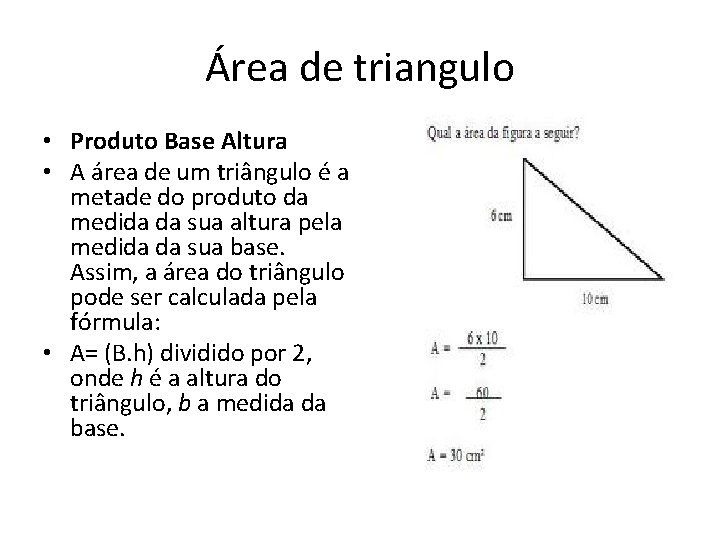
Área de triangulo • Produto Base Altura • A área de um triângulo é a metade do produto da medida da sua altura pela medida da sua base. Assim, a área do triângulo pode ser calculada pela fórmula: • A= (B. h) dividido por 2, onde h é a altura do triângulo, b a medida da base.

Feito pela aluna Giovana Oliveira Trabalho para o módulo de D. G.