Propositional Logic Calculations with Symbols Motivations Computers are

Propositional Logic: Calculations with Symbols

Motivations • Computers are logical machines. The first AI representational language that we are going to learn is, naturally, a logical language. • The simplest logical language capable of reasoning is call propositional calculus or propositional logic.

Objectives 1. 2. 3. 4. 5. 6. 7. Define propositions. Interpreting propositions (semantics). Operating on propositions. Interpreting these operations. Prove by truth table. Prove by modus ponens. Prove by modus tollens.

What are propositions? • Examples – Dolphin is a fish. – Dolphin is a mammal. – Dolphin is not a fish. – The moon is made of chess. • Non-examples – Dolphin possibly is a fish. – Dolphin may be a fish. – Is dolphin a fish? – What is the meaning of life? • A proposition is a sentence that may be asserted as either true or false in some (fictitious or real) world or discourse. • Reality is not important; Logical consistency is.

Truth value assignments • Proposition: Dolphin is a fish. • Assign a truth value to a proposition. • Two possibilities: – “Dolphin is a fish” is true. – “Dolphin is a fish” is false. • These are the only possibilities. • Exactly one of them must be correct. • Cannot be half true, 30% true, or any fraction thereof.

Propositions and variables • Let P be the sentence: "X is a person" – Is P a proposition? – Yes, if X is a constant. – No, if X is a variable. – Propositional logic cannot access parts of a sentence but only the whole sentence.

Propositional symbols

Proposition and interpretation • Proposition: Today is Sunday. • It could be true or false and nothing else. • One interpretation: Assert the proposition as true. • Another interpretation: Assert the proposition as false. • In this way an interpretation provides meaning or semantic values to the proposition.

Truth assignments • Let P denotes the proposition “it is snowing. ” • Let Q denotes the proposition “I am at work. ” • The set {P, Q} has 4 different evaluations or truth assignments. Evaluation No. P Q 1 T T 2 T F 3 F T 4 F F • Formally, an evaluation is an assertion about the truth of some propositions in some possible world.

Interpretation or evaluation 4

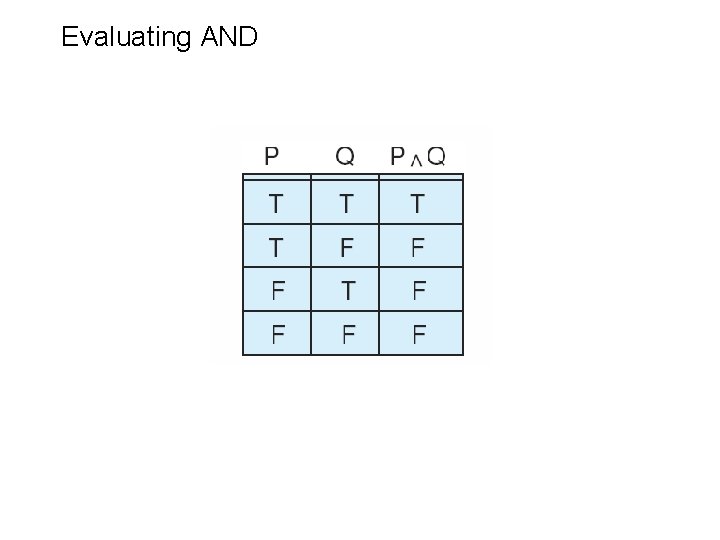
Evaluating AND

Conditional Given the propositions p and q, we can make the conditional p q (“If p, then q”). Sometimes also denoted as p q p part is called the antecedent q part is called the consequent Note: 3 out of 4 are True; if p is false, p q is always true Subjunctive conditional: Do not think in terms of cause and effect. The sentence “If today is Sunday then I am the richest man in the world” is true.

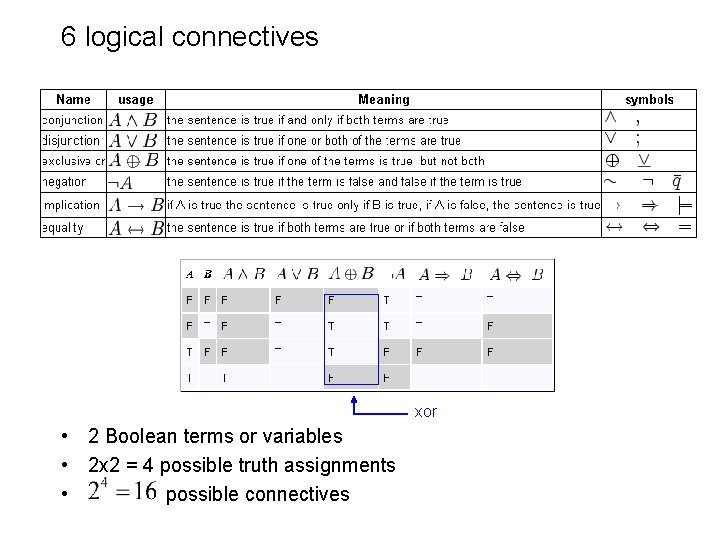
6 logical connectives xor • 2 Boolean terms or variables • 2 x 2 = 4 possible truth assignments • possible connectives

Important Equivalences Idempotent laws: p p p and p p p Double negation law: ¬ ¬ p p De Morgan’s laws: ¬(p q) ¬p ¬q ¬(p q r) ¬p ¬q ¬r Commutative laws: p q q p Associative laws: p (q r) (p q) r Distributive laws: p (q r) (p q) (p r) Law of contrapositive: p q ¬q ¬p If it is raining, then the ground is wet. If the ground is not wet, then it is not raining.

P Q ¬P Q • P = if it is raining • Q = the ground is wet • • • If it is raining, then the ground is wet. But the ground is not wet. Therefore, it is not raining. So, if the ground is not wet, then it is not raining. That is: either it is not raining or the ground is wet. P Q is equivalent with (¬ P Q)

Logical Equivalence of Conditional and Contrapositive One way to check for logical equivalence is to see if the truth tables of both variants have identical last columns: p q p q ¬q ¬p

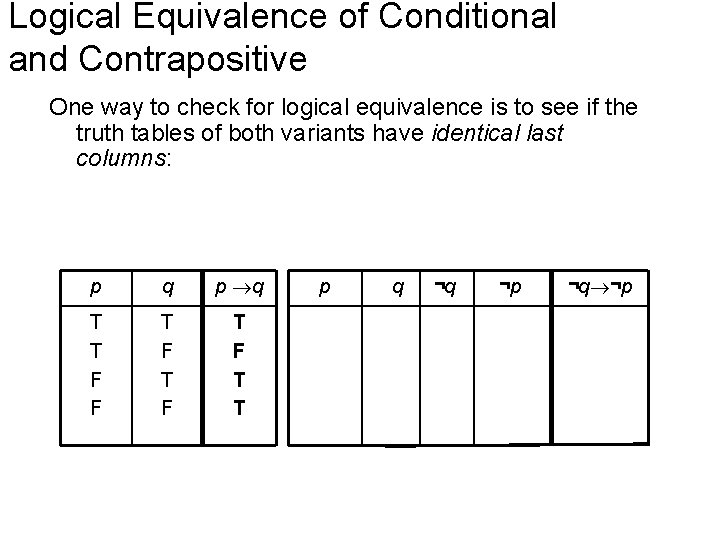
Logical Equivalence of Conditional and Contrapositive One way to check for logical equivalence is to see if the truth tables of both variants have identical last columns: p q T T F F T F T T p q ¬q ¬p

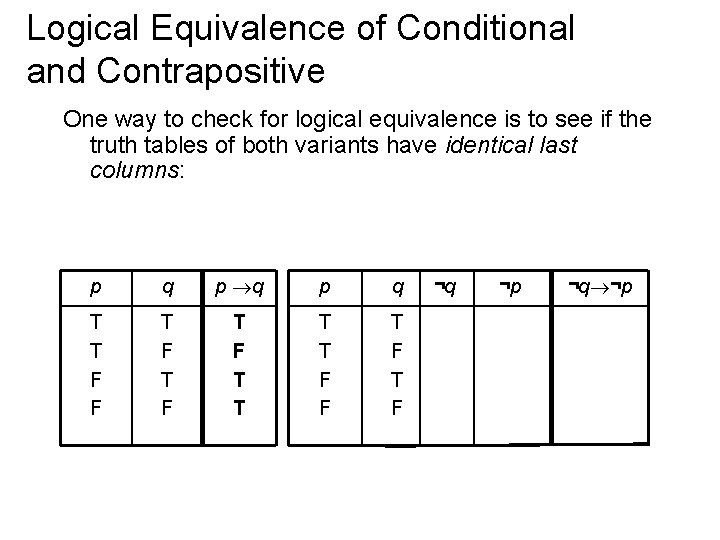
Logical Equivalence of Conditional and Contrapositive One way to check for logical equivalence is to see if the truth tables of both variants have identical last columns: p q p q T T F F T F T T T T F F T F ¬q ¬p

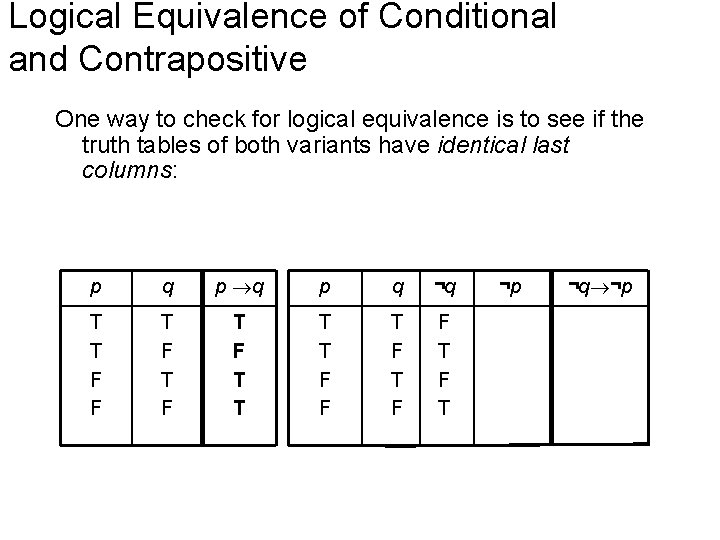
Logical Equivalence of Conditional and Contrapositive One way to check for logical equivalence is to see if the truth tables of both variants have identical last columns: p q p q ¬q T T F F T F T T T T F F T F T ¬p ¬q ¬p

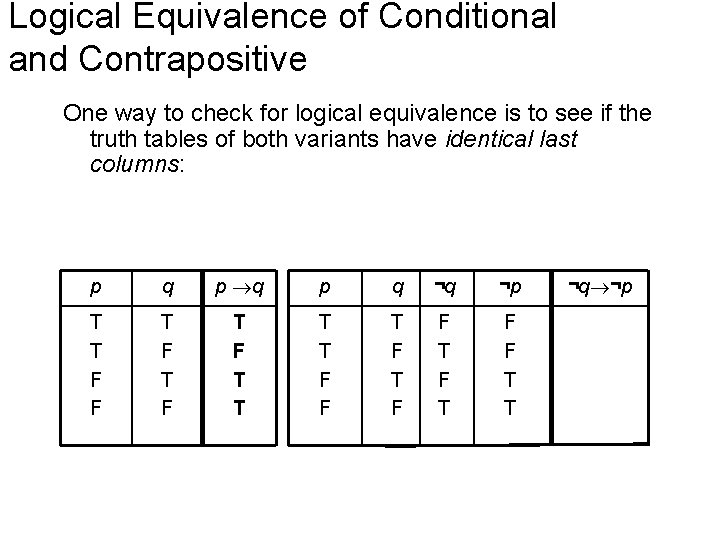
Logical Equivalence of Conditional and Contrapositive One way to check for logical equivalence is to see if the truth tables of both variants have identical last columns: p q p q ¬q ¬p T T F F T F T T T T F F T F T F F T T ¬q ¬p

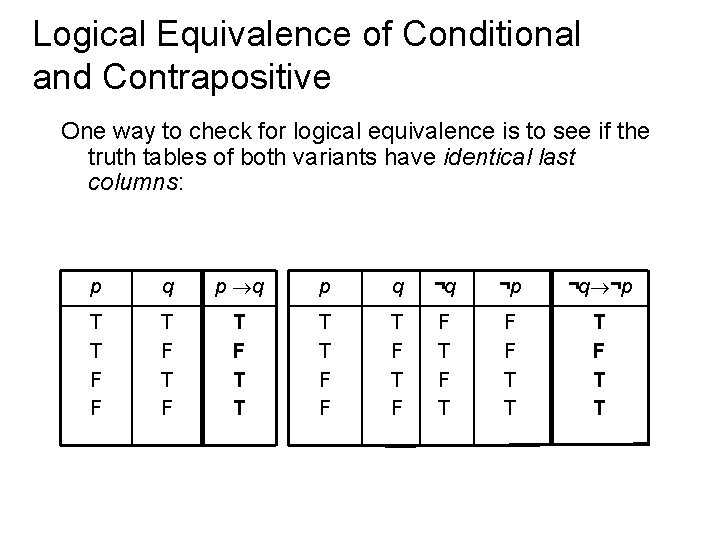
Logical Equivalence of Conditional and Contrapositive One way to check for logical equivalence is to see if the truth tables of both variants have identical last columns: p q p q ¬q ¬p T T F F T F T T T T F F T F T F F T T T F T T

Tautology • ταυτολογία • A propositional sentence that is always true no matter how you evaluate it. • Under any possible evaluation (truth assignment) of its propositional variables, the final result is always true. • The sentence p p is a tautology. Something must either be true or not true. There is no 3 rd possibility under classical propositional logic. p p F T T

Self-contradiction • A propositional sentence that is always false no matter how you assign the truth value to its variables. • The English sentence "I am lying" is selfcontradictory. • The sentence p p is a self-contradiction. A thing cannot be true and not true at the same time. p p F T T F F F

Inference • Proposition 1: Right now it is Monday 12: 55. • Proposition 2: If it is Monday between 12: 35 and 13: 20 pm, then we have an AI lecture. • Conclusion: Therefore, right now we have an AI lecture. • In stead of calculating a number from other numbers, propositional logic calculates propositions from other propositions.

Modus ponens and modus tollens • Given sentences P Q and P, by modus ponens, infer Q. • Given sentences P Q and Q, by modus tollens, infer P.

AI logical paradigm • Data structure: representation: syntax – How to represent a proposition. • Control structure: Reasoning: search – How to create, deduce, derive, or prove new propositions.

Summary • Propositions must be either true or (xor) false. Uncertainties are not allowed. • Propositions can be joined together by connectives to form propositional sentences. • Every statement can be evaluated to either true or false. • The language of propositional logic provides a formal means of expressing and calculating old propositions to get new propositions.