Propositional Logic Boolean Functions and Expressions CS 270

Propositional Logic: Boolean Functions and Expressions CS 270: Mathematical Foundations of Computer Science Jeremy Johnson

Propositional Calculus Objective: To provide students with the concepts and techniques from propositional calculus so that they can use it to codify logical statements and to reason about these statements. To illustrate how a computer can be used to carry out formal proofs and to provide a framework for logical deduction. 2

Propositional Calculus Topics Motivation: Logical Reasoning Boolean Functions Syntax and Semantics of Boolean Expressions Equivalence of Boolean Functions and Boolean Expressons Evaluating Boolean Expressions Truth tables and Disjunctive Normal Form (DNF)

Word Problem Tom likes Jane if and only if Jane likes Tom. Jane likes Bill. Therefore, Tom does not like Jane. Let p denote “Tom likes Jane” Let q denote “Jane likes Tom” Let r denote “Jane likes Bill” ((p q) r) p encodes the above claim The claim is not valid as the assignment p = true, q = true, and r = true evaluates to false

Limitations of Propositional Calculus Propositions hide the information in the predicates they abstract. Sometimes properties of the hidden information is required to make further deductions. E. G. for integers a, b, and c, (a < b) && (b < c) implies that a < c; however, this can not be deduced without using the order properties of the integers. The predicate calculus allows the use of predicates to encode this additional information. E. G. we can introduce a parameterized predicate lt(a, b) to encode the predicate a < b. Properties such as lt(a, b) && lt(b, c) lt(a, c) can be asserted. This type of notation and deduction is called predicate calculus and will be discussed later. 5

Boolean Functions A Boolean variable has two possible values (true/false) (1/0). A Boolean function has a number of Boolean input variables and has a Boolean valued output. A Boolean function can be described using a truth table. n 2 There are 2 Boolean function of n variables. s x 0 x 1 f x 0 f x 1 s 0 0 0 1 0 1 1 0 0 0 1 1 1 1 0 0 1 1 Multiplexor function 6

Grammars Recursive description of patterns Non-terminals (place holders) Terminals Production rules: Non-terminal string of terminals and non-terminals Start symbol Derivation: Apply rules, starting with start symbol until there are no non-terminals All strings derived this way comprise the language generated by the grammar 7

Boolean Expression Grammar BExpr : = Constant #t|#f Variable symbol Not BExpr And BExpr Or BExpr Bexpr Language defined by this grammar called well formed formulas (WFF) 8

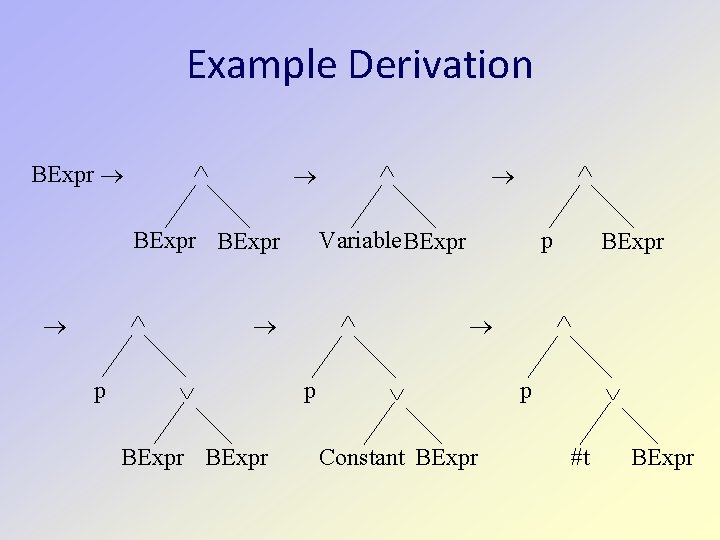
Example Derivation BExpr p Variable. BExpr p p Constant BExpr p #t BExpr

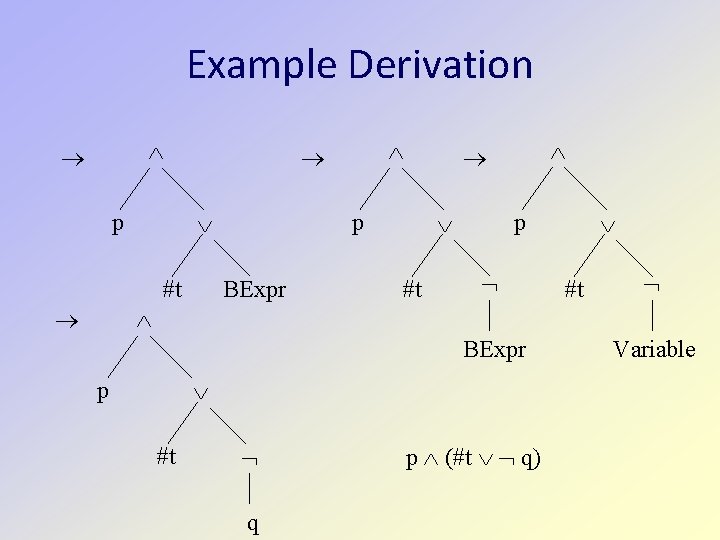
Example Derivation p #t p BExpr #t p #t BExpr p #t q p (#t q) Variable

Parse Tree A valid derivation can be represented by a tree whose nodes are labeled by the subexpression that is generated and whose children correspond to the rhs of the rule p (#t q) p (#t q) #t q q

Expression Trees Boolean expressions can be represented by a binary tree Internal nodes are operators Leaf nodes are operands Consider p (#t q): p #t q

Predicate for Boolean Expressions ; return true if the input expr is a Boolean expression (define (booleanexpr? expr) (cond [ (constant? expr) #t ] [ (variable? expr) #t ] [ (not? expr) (booleanexpr? (op 1 expr)) ] [ (or? expr) (and (booleanexpr? (op 1 expr)) (booleanexpr? (op 2 expr))) ] [ (and? expr) (and (booleanexpr? (op 1 expr)) (booleanexpr? (op 2 expr))) ] [ else #f ] ) ) 13

Semantics of Boolean Expressions An expression built up from variables, and, or, and not. x y x y x x 0 0 0 0 1 1 1 0 0 1 1 1 1 and or not 14

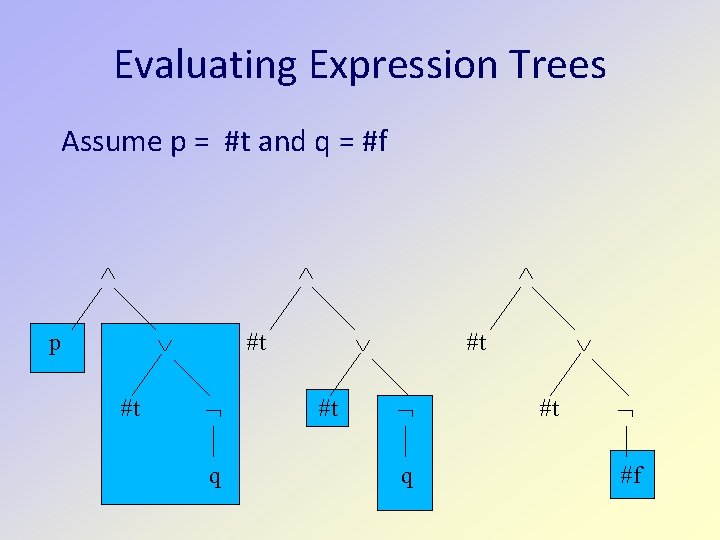
Evaluating Expression Trees Assume p = #t and q = #f p #t q #t #f

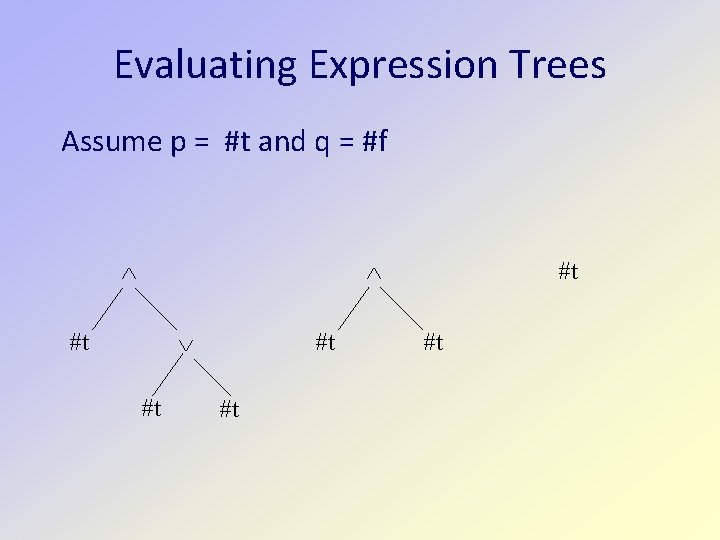
Evaluating Expression Trees Assume p = #t and q = #f #t #t #t

Evaluation ; Input: expr is a Boolean Expression, env is an environment of variable ; assignments to #t or #f. Assume all variables in expr are defined in env ; Output: #t if expr evaluates to true and #f if expr evaluates to false (define (bool-eval expr env) (cond [ (constant? expr) expr ) [ (variable? expr) (lookup expr env) ) [ (not? expr) (not (bool-eval (op expr) env)) ) [ (or? expr) (or (bool-eval (op 1 expr) env) (bool-eval (op 2 expr) env)) ) [ (and? expr) (and (bool-eval (op 1 expr) env) (bool-eval (op 2 expr) env)) ] ))

Short Circuit Evaluation ; Input: expr is a Boolean Expression, env is an environment of variable ; assignments to #t or #f. Assume all variables in expr are defined in env ; Output: #t if expr evaluates to true and #f if expr evaluates to false (define (sc-eval expr env) (cond [ (constant? expr) expr ] [ (variable? expr) (lookup expr env) ] [ (not? expr) (not (sc-eval (op expr) env)) ] [ (or? expr) (if (sc-eval (op 1 expr) env) #t (sc-eval (op 2 expr) env) ) ] [ (and? expr) (if (sc-eval (op 1 expr) env) (sc-eval (op 2 expr) env) #f ) ] ))

Disjunctive Normal Form A Boolean expression is a Boolean function Any Boolean function can be written as a Boolean expression Write a Boolean expression that evaluates to true for each row in the truth table that is true and false for other rows. The Boolean expression for a given row is the conjunction of the variables that are true and the negation of variables that are false. Take the disjunction of all such rows. E. G. (multiplexor function) ( s x 0 x 1 ) (s x 0 x 1 ) s x 0 x 1 f 0 0 0 1 0 1 1 0 0 0 1 1 1 1 0 0 1 1 19

Additional Notation Several additional Boolean functions of two variables have special meaning and are given special notation. By our previous results we know that all boolean functions can be expressed with not, and or; so the additional notation is simply a convenience. x y 0 0 1 1 1 implication x y x y 0 0 1 0 1 0 0 1 1 1 Equivalence (iff) x y 0 0 1 1 1 0 xor 20

Reduction to Boolean Expression x y Proof by truth table x y x y x y 0 0 1 0 1 1 1 0 0 1 1 1 21

Reduction to Boolean Expression (x y) (y x) Proof by truth table x y x y x y y x (x y) (y x) 0 0 1 1 1 0 0 1 0 0 1 1 1 1 1 22