Proportional Relationships The connection of Unit rates lines







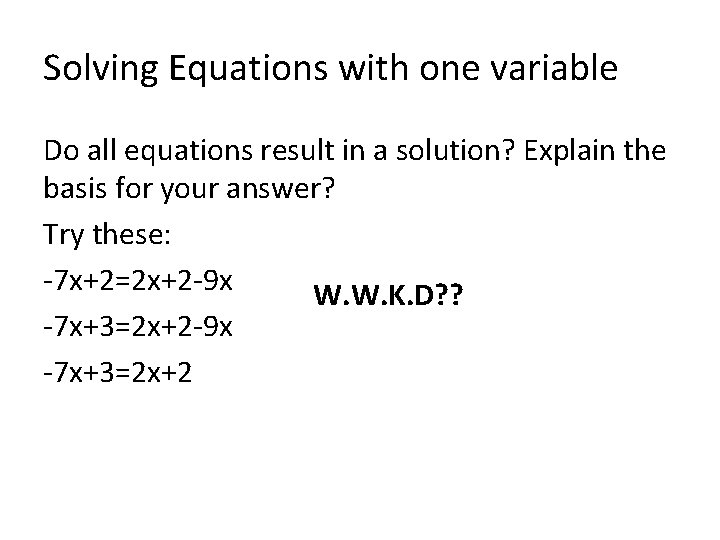









- Slides: 18

Proportional Relationships The connection of Unit rates, lines, and linear equations

How important is the =sign? • = sign means there is a relationship. – Numbers can be expressed as sum: 6=1+5 – 6 x 7=5 x 7+7 – Distributive property: 7(1+5)+7=7(1)+7(5)+7

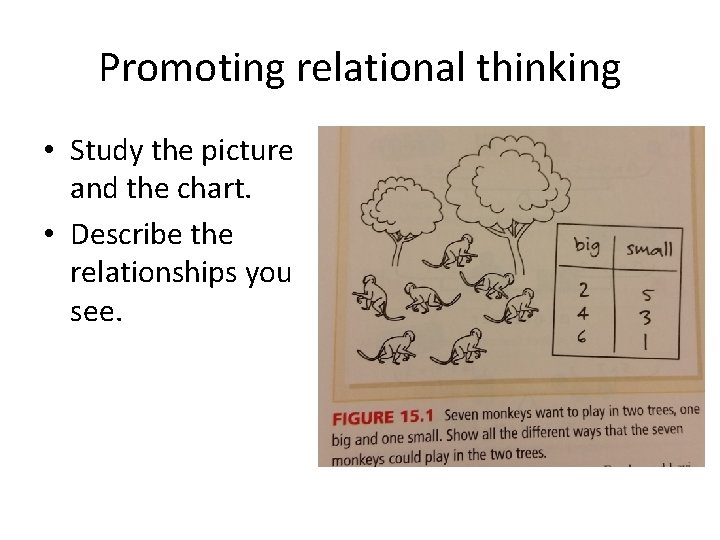
Promoting relational thinking • Study the picture and the chart. • Describe the relationships you see.

Promoting relational thinking cont. Talk with a partner to find two distinctly DIFFERENT explanations for why 5 should go in the box: 7 - = 6 – 4. How could we use relational thinking to solve: 534+175=174 + Hint: Don’t compute!! Think…

Exit Thinking Use relational thinking to determine if the relationships below are true or false. • Discuss the 1 st two problems with a partner; together you must decide if the relationships are true or false. • For the last two, work independently to explain your choice of true or false.

Challenge the teacher Groups of 3 or less Use today’s date to make up your own true/false sentences and have the teacher choose the correct response. • You can choose any operation combination, but YOU must be able to prove the answer choice as well. • Assignment worth 10 points

Exit ticket

Mathematical relationships: Equations & Graphs “=“ tells us that there is a relationship 7 x+2=2 x+2 -9 x • what is the relationship between the expressions f(x)=x listed above? f(x)=mx+b • Which of the “relationships” represent an equation, and which represents a linear equation?
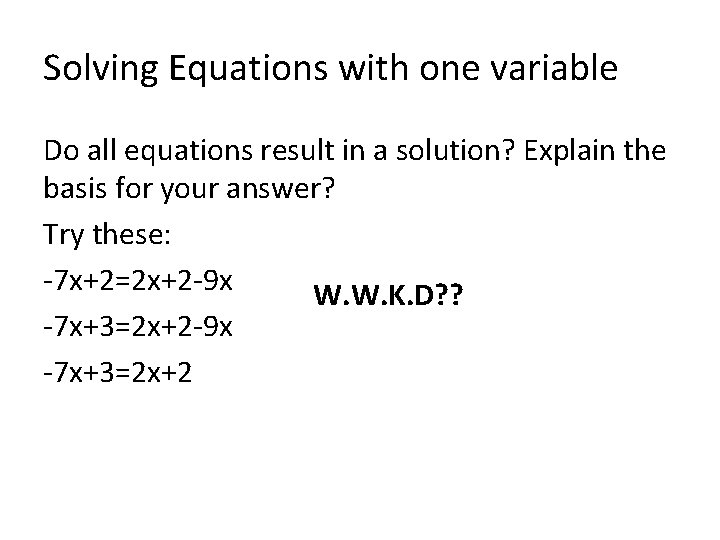
Solving Equations with one variable Do all equations result in a solution? Explain the basis for your answer? Try these: -7 x+2=2 x+2 -9 x W. W. K. D? ? -7 x+3=2 x+2 -9 x -7 x+3=2 x+2

y=x: “y is x” y=mx: y is the product of “m” and “x” y=mx+b: y is the sum of the product “mx and b” Thus: Y is a function of x

Relationship of functions •

Relationship of functions, cont. . The rule does NOT have to be mathematical… The rule could be a direction of what will happen after “a” for h(a) i. e: h is the rule that says: the next largest integer that starts with the same letter as a(this is the rule) so for a=2 what would h(a)=? What if a=8?

What do the graphs of functions look like? We have already used functions such as y=x+1. This says y is a function of x, such that y =x+1. f(y)=x+1. f(0)=1 f(1)=2 f(3)=? The graphs produce a “LINE”. The lines represent a linear equation. The equation is linear because its variables are solutions that represent CONTINUOUS ordered pairs when graphed on a coordinate plane. All equations don’t produce a line, but all functions produce lines, some straight some not….

Linear Functions explorations • f(x)=x • f(x)=mx+b Do these linear equations (functions) represent proportional equations? Why or Why not?

Linear functions(equations) of non-proportional relationships Linear equations can be written in the form y = mx + b. When b ≠ 0, the relationship between x and y is non-proportional. “the constant is “interrupted by the addition of a (+) or (-) value…”

The mathematician’s Rule “If the same symbol or letter appears more than once in an equation, then it must stand for the same number every place it occurs. ” + + 7 = +17 Use relational thinking to decide on a number that would make the statement true.

Conversely • More than one variable in a sentence will represent more than one value. • a+6=10 -b

What do proportional relationships look like? • Unit rates, constant of proportionality, straight lines that rise and run at a constant rate, and run through the origin of the graph. • Graphically- y=mx