Property 5 Refraction bending of light another way

Property 5: Refraction bending of light (another way than from reflection) Experiment? see the image → Particle (photon) explanation? Wave (E&M) explanation?

Property 5: Refraction Experiment: objects in water seem closer than they really are when viewed from air Light goes straight in water and straight in air, but it is bent when it goes from one to the other. eye air water apparent location real object

Property 5: Refraction Particle (photon) explanation for why ray is bent towards the surface in air and away from the surface in water? ray in air surface water ray in water

Property 5: Refraction Particle (photon) explanation: air ray in air vx-air vy-air v is velocity vx-air = vx-water vy-air < vy-water surface water vx-water therefore vair < vwater vy-water ray in water
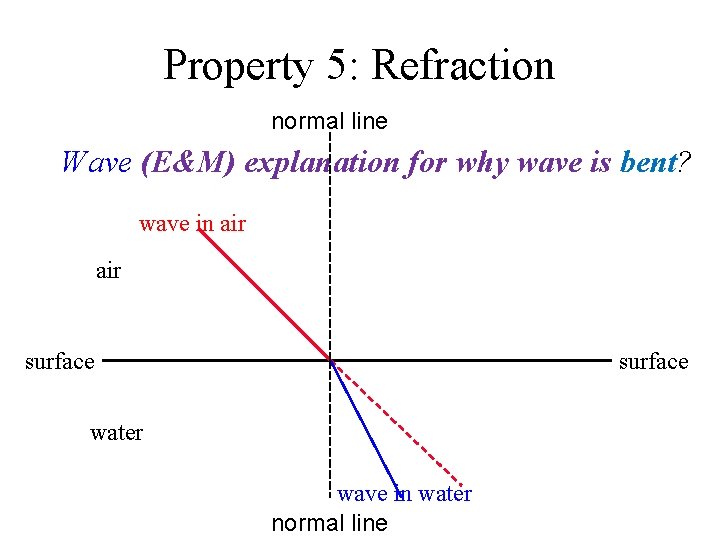
Property 5: Refraction normal line Wave (E&M) explanation for why wave is bent? wave in air surface water wave in water normal line

Property 5: Refraction Wave (E&M) explanation: crest of following wave is wavelength = distance from crest to crest of wave in air crest of preceding wave air x surface water wave in water normal line

Property 5: Refraction The frequency in both air and water must be the same, so a shorter wavelength in water means a smaller velocity for light in water. • Particle (photon) theory: vwater > vair • Wave (E&M) theory: vwater < vair • Experiment ?

Property 5: Refraction • Particle (photon) theory: vwater > vair • Wave (E&M) theory: vwater < vair • Experiment: vwater < vair wave theory works! particle theory fails!

Properties 1, 2 & 5 Speed, Color and Refraction • Speed of light changes in different materials • Speed (v) is related to frequency (f) and wavelength ( ): v = f • If speed changes, does wavelength change, frequency change, or BOTH (at least one of the two has to change)? • Does color change?

Properties 1, 2 & 5 Speed, Color and Refraction • Speed of light changes in different materials • Speed is related to frequency and wavelength: v = f What changes with speed? – Frequency remains constant regardless of speed – Wavelength changes with speed – Color remains the same regardless of speed – so color depends on frequency, not wavelength

Refraction and Thin Lenses We can use refraction to try to control rays of light to go where we want them to go. Let’s see if we can FOCUS light.
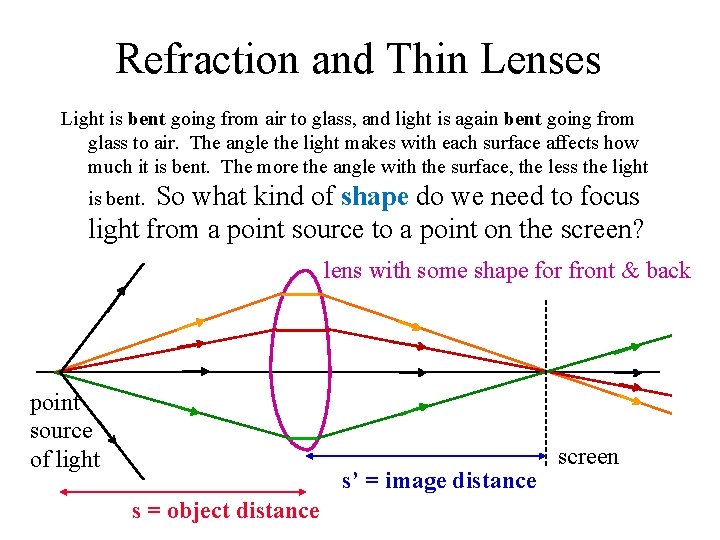
Refraction and Thin Lenses Light is bent going from air to glass, and light is again bent going from glass to air. The angle the light makes with each surface affects how much it is bent. The more the angle with the surface, the less the light So what kind of shape do we need to focus light from a point source to a point on the screen? is bent. lens with some shape for front & back point source of light s’ = image distance s = object distance screen

Refraction and Thin Lenses and the Eye Is this also how a camera works? Yes! The camera has a lens that focuses the light on the photographic film (old style) or light sensitive electronic detectors (new digital style) which are placed where the screen would be. Is this how the eye works? YES! The eye has a lens that focuses the light onto the back of the eye, the retina, that has light sensitive cells. When each cell is hit with light, it sends a signal to the brain along the optic nerve. The brain then sorts through all of the signals and we see the image (in our head).

Refraction and Thin Lenses What kind of shape should a lens have in order to focus the light? Let’s try a simple (easy to make) shape: SPHERICAL. A spherical shape has a constant curvature of its surface – it curves the same everywhere. Play with the lens that is handed out (either in lecture or in lab) 1. Does it act like a magnifying glass?

Refraction and Thin Lenses Let’s try a simple (easy to make) shape: SPHERICAL. Play with the lens that is handed out (either in lecture or in lab) 1. Does it act like a magnifying glass? 2. Does it focus light from the night light?

Refraction and Thin Lenses Let’s try a simple (easy to make) shape: SPHERICAL Play with the lens that is handed out 1. Does it act like a magnifying glass? 2. Does it focus light from the night light? 3. Does the image distance (distance from lens to screen when focused properly) depend on the shape of the lens? (Trade with your neighbor to get a different shaped lens. )

Refraction and Thin Lenses Spherical shape is specified by a radius. The smaller the sphere (smaller the radius), the more curved is the surface! R R R 2 R 1

Focal length A lens is made from a transparent material, and it has a front and back curvature (radii). The material has its own speed for light and so it has its own ability to bend light due to refraction. We assign a parameter called the index of refraction to this material based on its ability to bend light. The front and back sides of the lens are specified by the radius of curvature. If we put this all together, we come up with a single number called the focal length, f, that describes each lens.

Focal Length The focal length describes how strongly the lens will bend the light. A small focal length will bend the light more than a larger focal length. A lens with a small focal length will then perform as a strong magnifying lens, and a large focal length lens will only weakly magnify. These type lenses can be used to correct far sightedness (where the eye has too weak of a lens).

Focal Lengths Focal lengths can be negative if we have opposite curvatures for the two sides. These lenses will de-magnify. These can be used to correct near sightedness (where the eye has too strong of a lens). The optometrist uses a measure called diopters instead of focal length to describe the strength of a lens, where the number of diopters = 1 / focal length when the focal length is measured in meters. For example a lens with a strength of 5 diopters has a focal length of f = 1 / (5/m) = (1/5)m = 0. 2 m = 20 cm. Small focal lengths indicate a strong lens (counter-intuitive) whereas large diopters indicate a strong lens (more intuitive).

Focal Length A lens’ ability to bend the light, described by its focal length, will connect the distance an object is from the lens (called the object distance, s) to the distance the image formed by the lens is from the lens (called the image distance, s’). This is shown in the next several slides. The next slide shows a strong lens that bends the light a lot; the following slides show a weaker lens that does not bend the light as much.

Refraction and the Lens-users Eq. A strong lens with a small focal length bends the light a lot f>0 s > 0 AND s > f s’ > 0 AND s’ > f f f s s’ Example: f = 5 cm; s = 10 cm; s’ = 10 cm: 1/10 cm + 1/10 cm = 1/5 cm 20 diopters
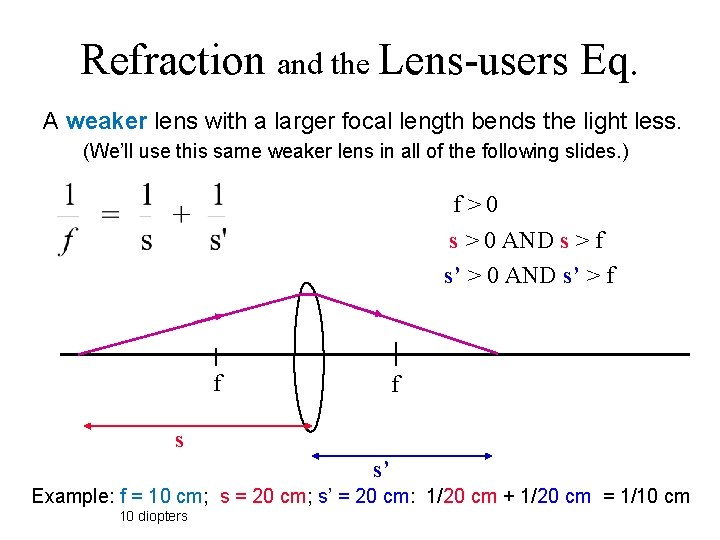
Refraction and the Lens-users Eq. A weaker lens with a larger focal length bends the light less. (We’ll use this same weaker lens in all of the following slides. ) f>0 s > 0 AND s > f s’ > 0 AND s’ > f f f s s’ Example: f = 10 cm; s = 20 cm; s’ = 20 cm: 1/20 cm + 1/20 cm = 1/10 cm 10 diopters
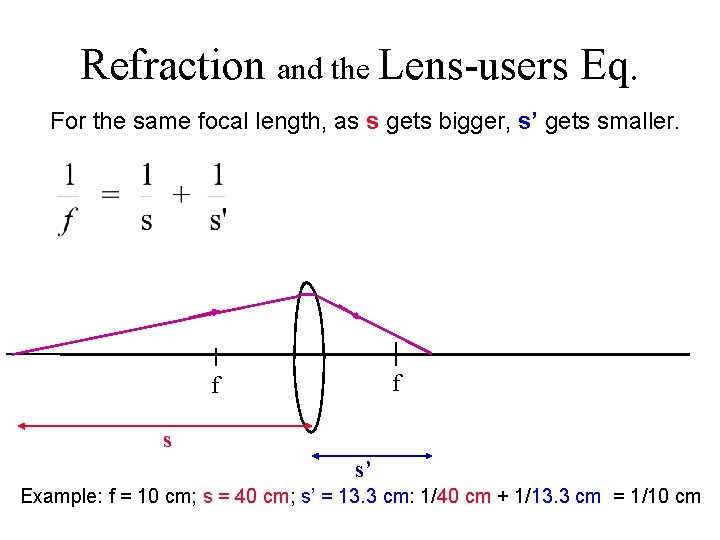
Refraction and the Lens-users Eq. For the same focal length, as s gets bigger, s’ gets smaller. f f s s’ Example: f = 10 cm; s = 40 cm; s’ = 13. 3 cm: 1/40 cm + 1/13. 3 cm = 1/10 cm
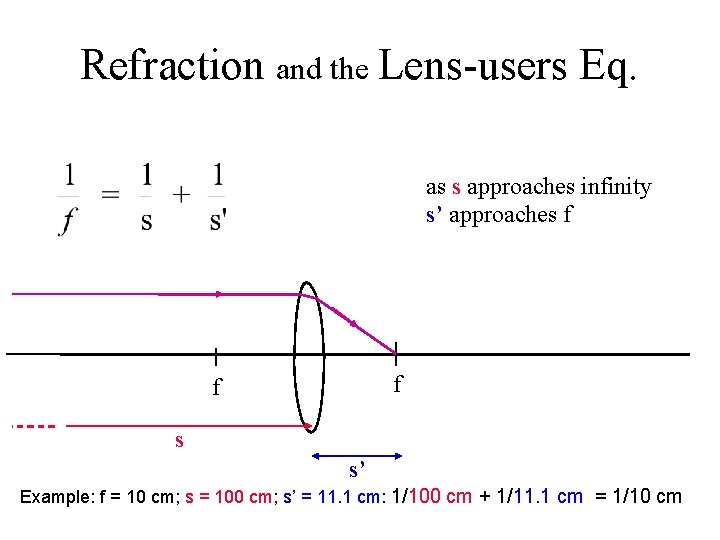
Refraction and the Lens-users Eq. as s approaches infinity s’ approaches f f f s s’ Example: f = 10 cm; s = 100 cm; s’ = 11. 1 cm: 1/100 cm + 1/11. 1 cm = 1/10 cm
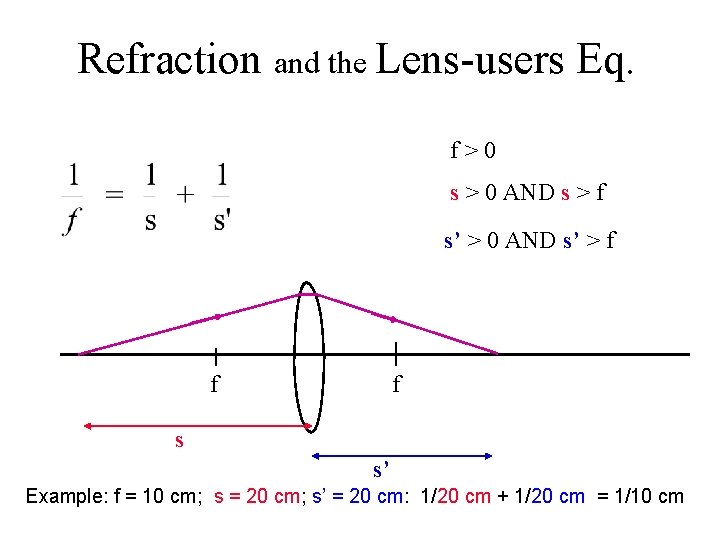
Refraction and the Lens-users Eq. f>0 s > 0 AND s > f s’ > 0 AND s’ > f f f s s’ Example: f = 10 cm; s = 20 cm; s’ = 20 cm: 1/20 cm + 1/20 cm = 1/10 cm
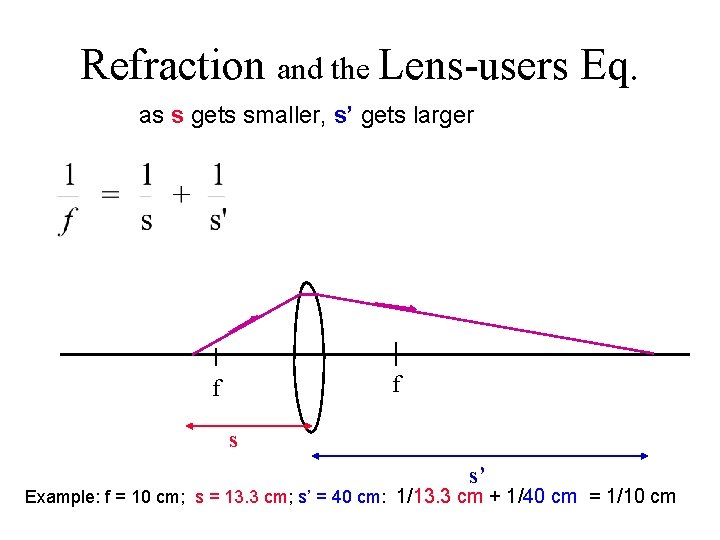
Refraction and the Lens-users Eq. as s gets smaller, s’ gets larger f f s s’ Example: f = 10 cm; s = 13. 3 cm; s’ = 40 cm: 1/13. 3 cm + 1/40 cm = 1/10 cm
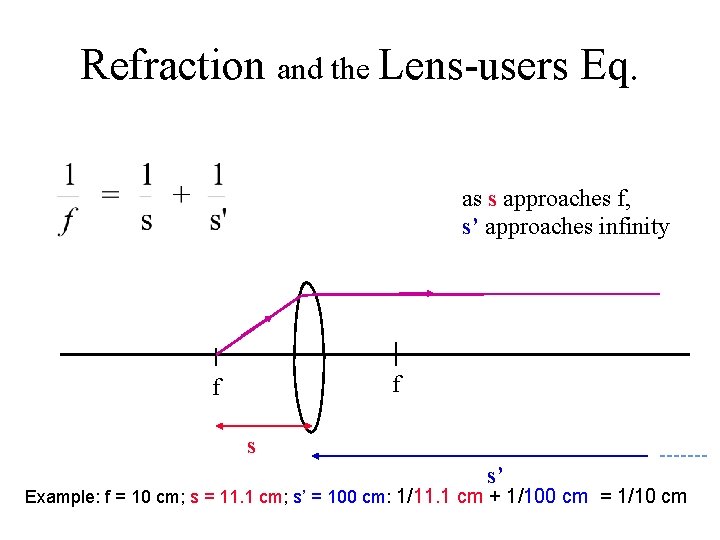
Refraction and the Lens-users Eq. as s approaches f, s’ approaches infinity f f s s’ Example: f = 10 cm; s = 11. 1 cm; s’ = 100 cm: 1/11. 1 cm + 1/100 cm = 1/10 cm

Refraction and the Lens-users Eq. Before we see what happens when s, the distance of the object to the lens, gets smaller than f, the focal length, let’s use what we already know to see how the lens will work.

Refraction and the Lens-users Eq. – Any ray that goes through the focal point on its way to the lens, will come out parallel to the optical axis. (ray 1) f f ray 1

Refraction and the Lens-users Eq. – Any ray that goes through the focal point on its way from the lens, must go into the lens parallel to the optical axis. (ray 2) f f ray 1 ray 2

Refraction and the Lens-users Eq. – Any ray that goes through the center of the lens must go essentially undeflected. (ray 3) object image f f ray 1 ray 3 ray 2
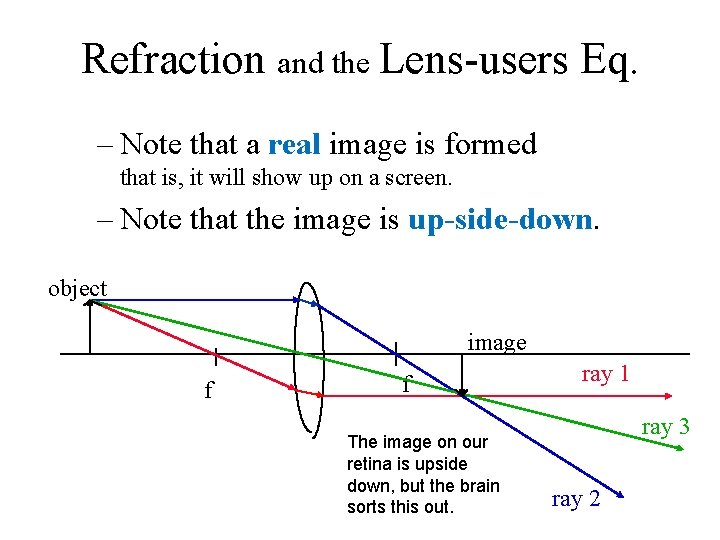
Refraction and the Lens-users Eq. – Note that a real image is formed that is, it will show up on a screen. – Note that the image is up-side-down. object image f f The image on our retina is upside down, but the brain sorts this out. ray 1 ray 3 ray 2

Refraction and the Lens-users Eq. – By looking at ray 3 alone, we can see by similar triangles that M = h’/h = -s’/s. object h s’ s f f image h’<0 ray 3 Example: f = 10 cm; s = 40 cm; s’ = 13. 3 cm: M = -13. 3 cm/40 cm = -0. 33 X note h’ is up-side-down and so is < 0
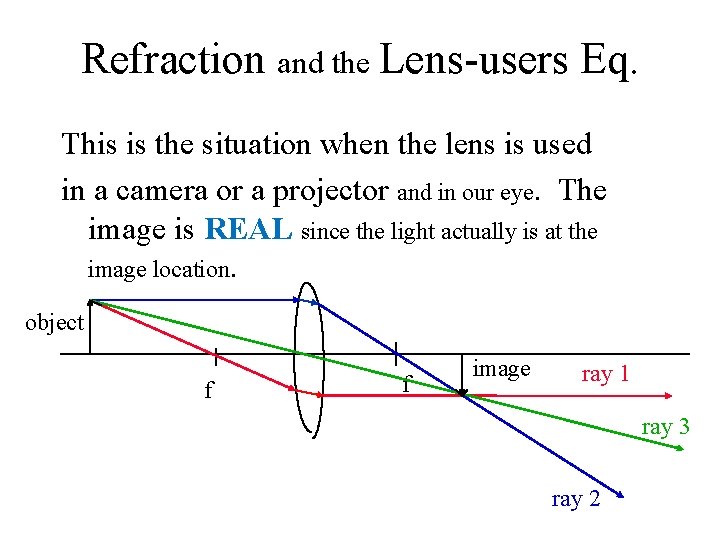
Refraction and the Lens-users Eq. This is the situation when the lens is used in a camera or a projector and in our eye. The image is REAL since the light actually is at the image location. object f f image ray 1 ray 3 ray 2

Refraction and the Lens-users Eq. What happens when the object distance, s, changes? object image f f ray 1 ray 3 S’ s ray 2

Refraction and the Lens-users Eq. Notice that as the object distance, s, gets bigger, the image distance, s’, gets closer to f, and the image height gets smaller. object image f f ray 1 S’ ray 3 s Example: f = 10 cm; s = 100 cm; s’ = 11. 1 cm: M = -11. 1 cm/100 cm = -0. 11 X ray 2

Focusing To focus a camera, we need to change s’ as s changes. To focus a projector, we need to change s as s’ changes. We do this by screwing the lens closer or further from the film or slide. But what about the eye? How do we focus on objects that are close and then further away with our eyes? Do we screw our eyes in and out like the lens on a camera or projector?

Focusing But what about the eye? How do we focus on objects that are close and then further away with our eyes? Do we screw our eyes in and out like the lens on a camera or projector? NO, instead our eyes CHANGE SHAPE and hence change their focal length, f, as s changes, keeping s’ the same!

Refraction and the Lens-users Eq. Let’s now look at the situation where s < f (but s is still positive): f s f

Refraction and the Lens-users Eq. We can still use our three rays. Ray one goes through the focal point on the left side. ray 1 f s f
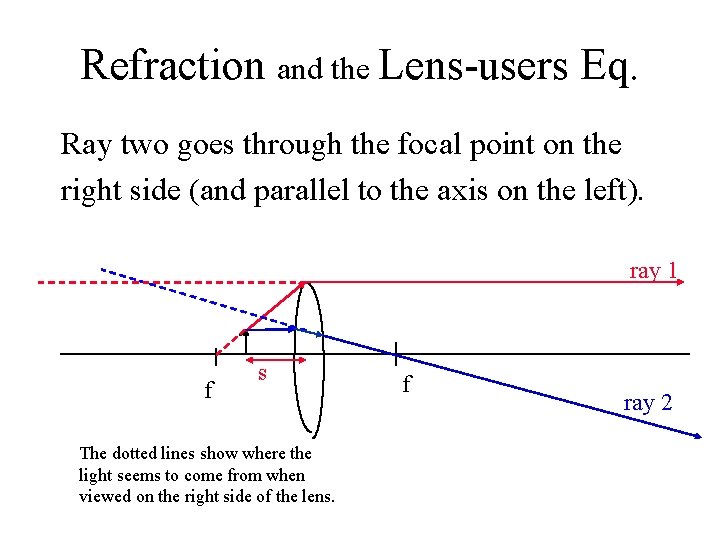
Refraction and the Lens-users Eq. Ray two goes through the focal point on the right side (and parallel to the axis on the left). ray 1 f s The dotted lines show where the light seems to come from when viewed on the right side of the lens. f ray 2
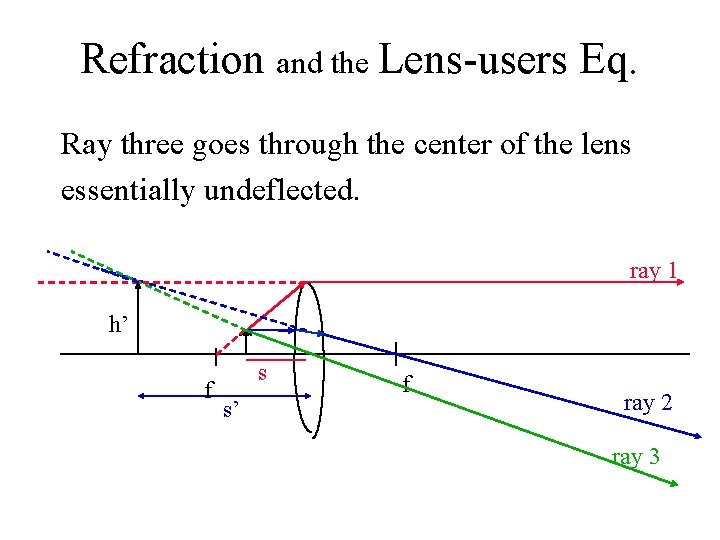
Refraction and the Lens-users Eq. Ray three goes through the center of the lens essentially undeflected. ray 1 h’ f s s’ f ray 2 ray 3

Refraction and the Lens-users Eq. Notice that: s’ is on the “wrong” side, which means that s’ < 0 , and that |s’| > |s| so f > 0. ray 1 h’ f s s’ f ray 2 ray 3 Example: f = 10 cm; s = 7. 14 cm; s’ = -25 cm, so 1/f = 1/7. 14 cm + 1/(-25 cm) = 1/10 cm which works!

Refraction and the Lens-users Eq. Notice that the image height, h’, is right-side-up and so h’ > 0, and it is bigger than the object height, h. M = h’/h so M > 0. h’ f s s’ f Example: f = 10 cm; s = 7. 14 cm; s’ = -25 cm: M = - (-25 cm)/ 7. 14 cm = 3. 5 X ray 3

Refraction and the Lens-users Eq. This is the situation when the lens is used as a magnifying glass! Image is VIRTUAL since the light does not actually go through the image position. The image will NOT show up on a screen. It is like the image in a mirror. ray 1 h’ f s s’ f ray 2 ray 3

Refraction and the Lens-users Eq. The same lens can be used as: • a camera lens: s >> f, s > s’, M < 0, |M| < 1 real image • a projector lens: s > f, s’ > s, M < 0, |M| > 1 real image • a magnifying glass: s < f, s’ < 0, M > 1 virtual image

Refraction and the Lens-users Eq. Notes on using a lens as a magnifying glass: • hold lens very near your eye • want IMAGE at best viewing distance which has the nominal value of 25 cm so that s’ = -25 cm.

Refraction and the Lens-users Eq. Are there any limits to the magnifying power we can get from a magnifying glass?

Refraction and the Lens-users Eq. Are there any limits to the magnifying power we can get from a magnifying glass? • A magnifying glass has limits on its magnifying ability due to its size since a small focal length (strong magnifying lens) demands a small radius for its curvature – which means a small lens. • Since the light goes through the magnifying glass which has a definite size opening, the light will not be focused to points but rather to fuzzy dots; the smaller the lens size and so more magnification, the bigger the spots and so the image will be less clear.

Need a two lens system Since a single lens can’t effectively magnifying beyond about 30 power, we need to go to a two lens system. We need a MICROSCOPE (two lens system) for near and small things; We need a TELESCOPE (two lens system) for far away things.
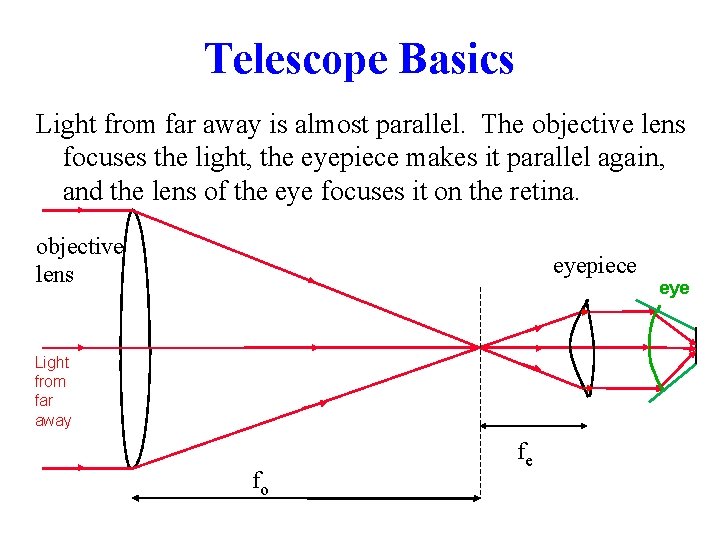
Telescope Basics Light from far away is almost parallel. The objective lens focuses the light, the eyepiece makes it parallel again, and the lens of the eye focuses it on the retina. objective lens eyepiece eye Light from far away fo fe
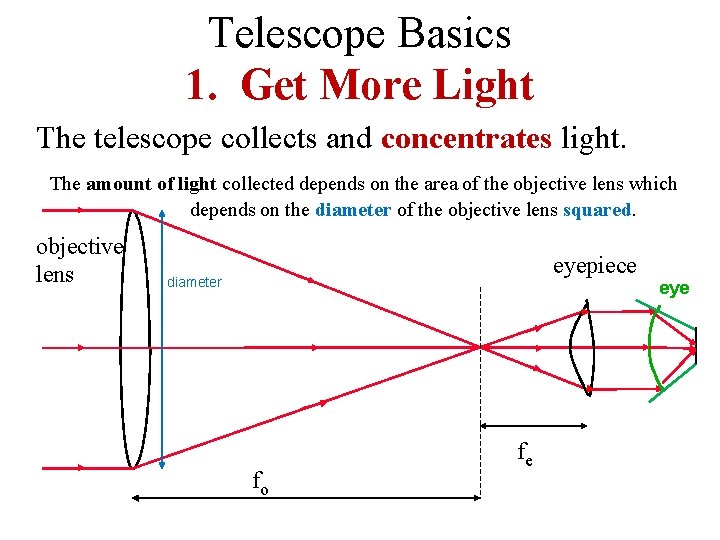
Telescope Basics 1. Get More Light The telescope collects and concentrates light. The amount of light collected depends on the area of the objective lens which depends on the diameter of the objective lens squared. objective lens eyepiece diameter eye fo fe
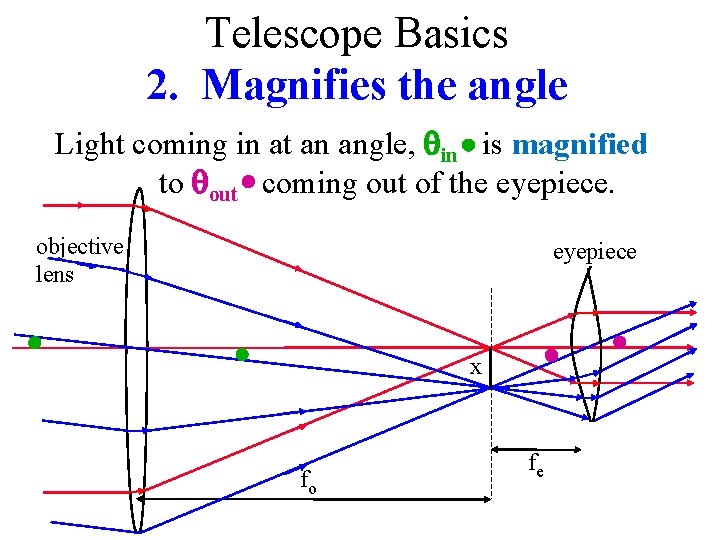
Telescope Basics 2. Magnifies the angle Light coming in at an angle, in is magnified to out coming out of the eyepiece. objective lens eyepiece x fo fe
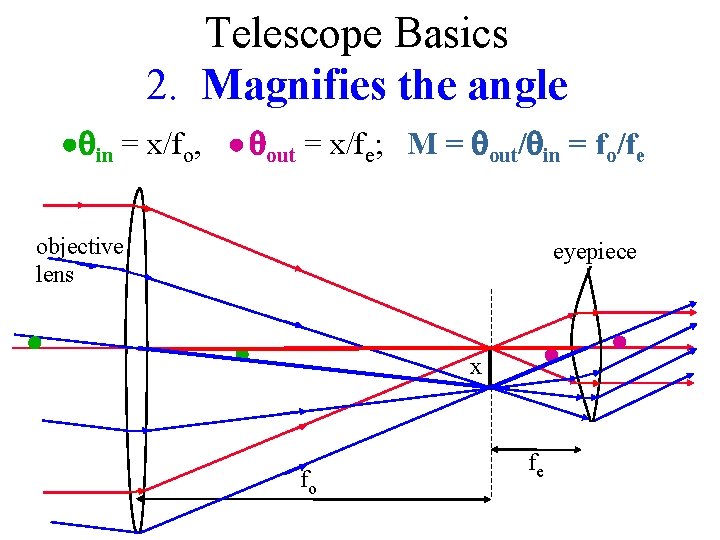
Telescope Basics 2. Magnifies the angle in = x/fo, out = x/fe; M = out/ in = fo/fe objective lens eyepiece x fo fe

Telescope Basics 3. Limits on Resolution Because light goes through the lenses, it is cut off by the edge of the lenses and this causes the light to be focused into fuzzy dots rather than ideal points of light. This causes the image to be a bit fuzzy. The ability to resolve clear images depends on both the wavelength of the light (λ) and the diameter (D) of the opening (diameter of the objective lens). If we have a magnification larger than the max useful, we only magnify a fuzzy image and can’t see any more detail. Resolution: 1. 22 = D sin( limit) so with in = limit and out = 5 arc minutes, (we’ll see in lab that most people can resolve about 2 -3 arc minutes) the limit 1/D the angle in is inversely proportional to the diameter of the objective lens implies Museful = 60 X/in * D. 60 X means 60 power

Limits on Resolution: calculation Mmax useful = out/ in = eye/ limit = 5 arc min / (1. 22 * / D) radians = (5/60)*( /180) / (1. 22 * 5. 5 x 10 -7 m / D) = (2167 / m) * D * (1 m / 100 cm) * (2. 54 cm / 1 in) = (55 / in) * D We can round this off to 60 power per inch. Examples: the maximum useful magnification of a 2 inch telescope (which means the diameter of the objective lens is 2 inches) would be 2*60 X = 120 power; the maximum useful magnification of an 8 inch telescope would be 8*60 X = 480 power. Since most people can resolve angles smaller than 5 arc minutes, this max useful magnification is really too high and should be lower.

Example What diameter telescope would you need to read letters the size of license plate numbers from a spy satellite?

Example What diameter telescope would you need to read letters the size of license plate numbers from a spy satellite? • need to resolve an “x” size of about 1 cm (1 cm is about 3/8 of an inch) • “s” is on order of 100 miles or 150 km • limit then must be (in radians) = 1 cm / 150 km = 7 x 10 -8 • limit = 1. 22 x 5. 5 x 10 -7 m / D = 7 x 10 -8 so D = 10 m (Hubble has a 2. 4 m diameter)

Limits on Resolution: further examples • other types of light – x-ray diffraction (use atoms as slits) – IR – radio & microwave • surface must be smooth on order of Since the wavelength of visible light is a little less than a micrometer, optical lenses must be polished to a smoothness of less than a micrometer. Since the wavelength of microwaves is on the order of centimeters, the smoothness of satellite dishes only needs to be smooth on the order of centimeters.

Review of Telescope Properties 1. Light gathering ability: depends on area of objective lens, so depends on diameter of objective lens squared (D 2). 2. Magnification: M = fo/fe depends on the focal lengths of the two lenses. 3. Resolution ability: depends on diameter of objective lens: Max magnification = 60 power/in * D. Since essentially all three properties of the telescope depend on the diameter of the objective lens, telescopes are often specified by the diameter of their objective lens.

Types of Telescopes The type of telescope we have looked at so far, and the type we have or will have made in the lab is called a refracting telescope, since it uses the refraction of light going from air to glass and back to air. This is the type used by Galileo. There is a second type of telescope invented by Newton. It is called the reflecting telescope since it uses a curved mirror instead of a curved lens for the objective. There are three main sub-types of reflectors that we’ll consider: Prime focus, Newtonian focus, and Cassegranian focus.
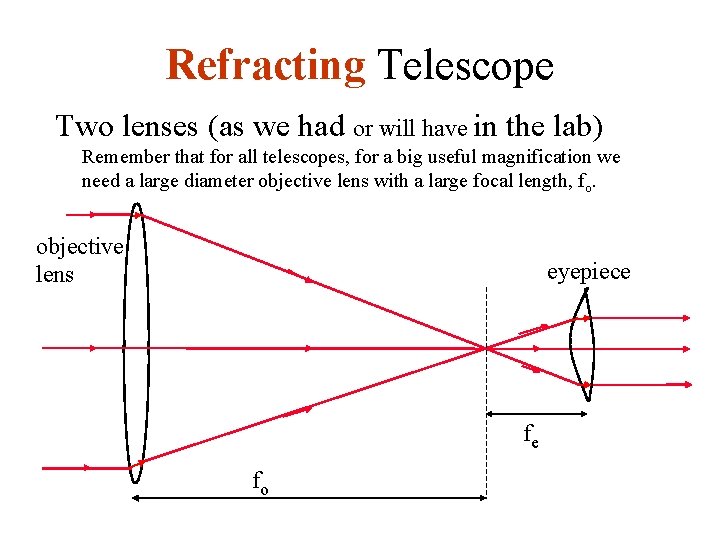
Refracting Telescope Two lenses (as we had or will have in the lab) Remember that for all telescopes, for a big useful magnification we need a large diameter objective lens with a large focal length, fo. objective lens eyepiece fe fo
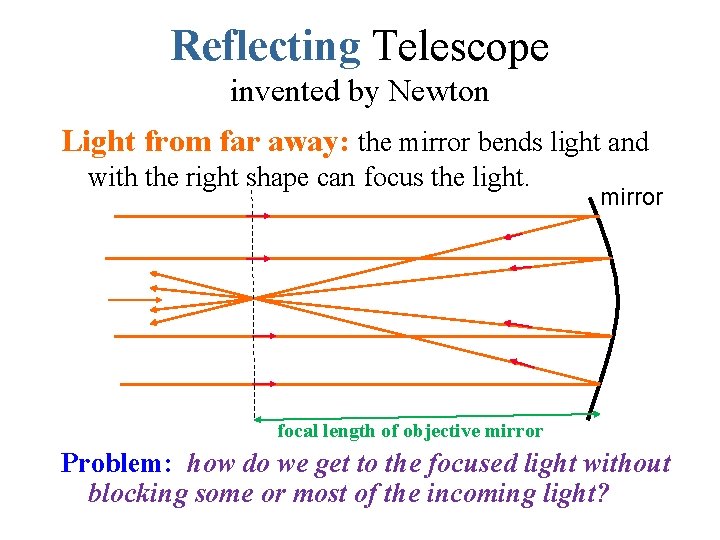
Reflecting Telescope invented by Newton Light from far away: the mirror bends light and with the right shape can focus the light. mirror focal length of objective mirror Problem: how do we get to the focused light without blocking some or most of the incoming light?
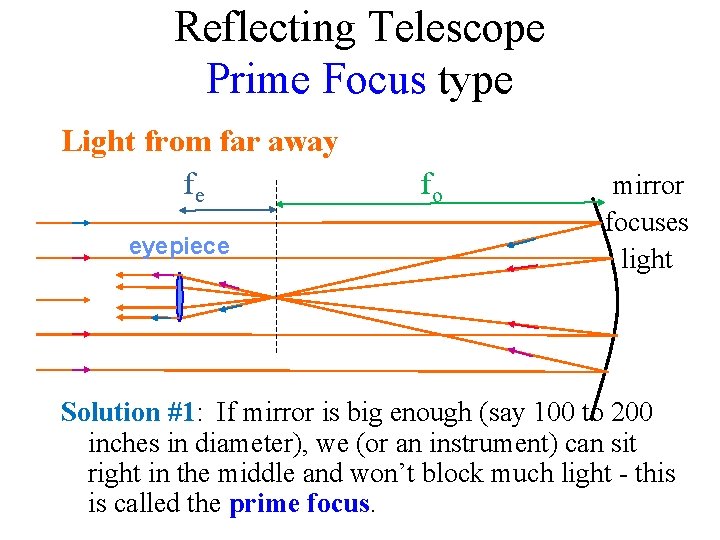
Reflecting Telescope Prime Focus type Light from far away fe eyepiece fo mirror focuses light Solution #1: If mirror is big enough (say 100 to 200 inches in diameter), we (or an instrument) can sit right in the middle and won’t block much light - this is called the prime focus.
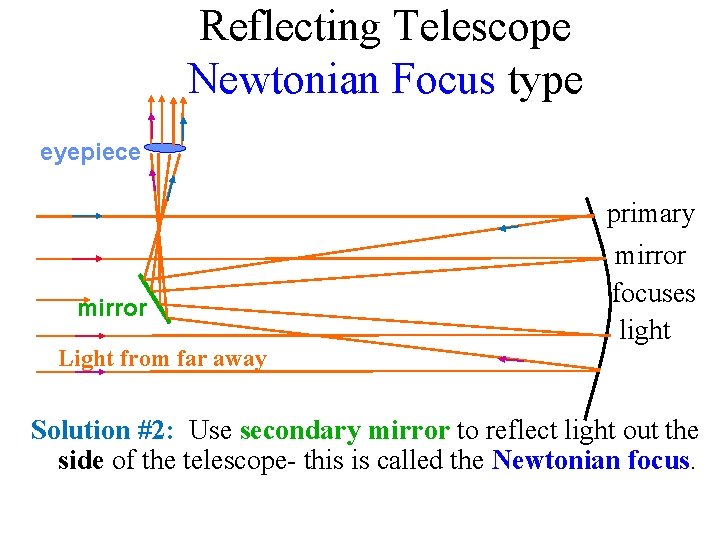
Reflecting Telescope Newtonian Focus type eyepiece primary mirror Light from far away mirror focuses light Solution #2: Use secondary mirror to reflect light out the side of the telescope- this is called the Newtonian focus.
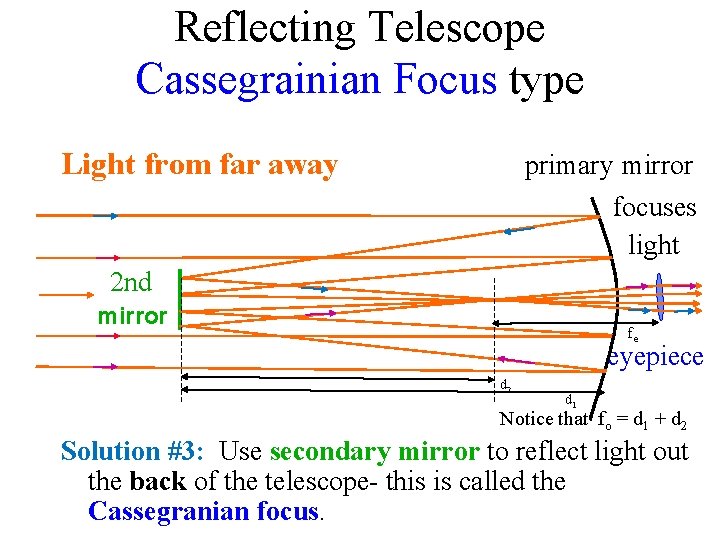
Reflecting Telescope Cassegrainian Focus type Light from far away primary mirror focuses light 2 nd mirror fe eyepiece d 2 d 1 Notice that fo = d 1 + d 2 Solution #3: Use secondary mirror to reflect light out the back of the telescope- this is called the Cassegranian focus.

Advantages: Refracting versus Reflecting Three advantages that a refracting telescope have, especially for a small telescope such as a hand held telescope or a telescope for a rifle, are that a refracting telescope is 1. simplest to make, 2. easiest to aim, and 3. nothing is in the path of the light like there is in a reflecting telescope. We did (or will) make this kind of telescope in lab.

Advantages: Reflecting versus Refracting 1. One advantage that a reflecting telescope has over a refracting one is that a mirror reflects all the colors the same, whereas a lens bends light slightly differently for different colors – called chromatic aberration. This effect is useful in a prism, but causes a blurry image in a lens. Chromatic aberration can be minimized for a lens if we use two different lenses made of different materials. For small lenses, this adds to the cost, but is quite do-able. For large lenses, this is very expensive!

Advantages: Reflecting versus Refracting 2. A second major advantage that a reflecting telescope has over a refracting one is that a mirror only has one side that needs to be polished, while a lens has two sides that need to be polished. This greatly reduces the cost of a large telescope.

Advantages: Reflecting versus Refracting 3. A third major advantage that a reflecting telescope has, especially for large telescopes, is that a mirror is much easier to mount than a lens. You can mount a mirror and hold it from the back, while a lens has to be held only by the edges. Almost all large telescopes are reflecting for these three reasons.

Review • Speed of light is correctly explained by the wave theory (E&M fields that oscillate in space). • Light has colors: different colors have different frequencies in the wave theory, different energies in the photon theory. • Some of the light will reflect when it hits a different material.

Review 2 • When light enters different materials, it is bent (refraction) depending on the angle it strikes and the materials. • Refraction allows the eye to focus the incoming light to form an image on the retina, and it allows us to build lenses to use in telescopes to better see “what’s up there”. • Wave theory is correct, particle is theory wrong in explaining refraction.

Review 3 • There are three main properties of a telescope, and all 3 depend on the diameter of the objective lens or mirror in some way: – Light gathering (depends on area of opening which depends on the diameter squared of the objective lens or mirror) – Magnification (M = fo/fe) – Resolution (depends on diameter of the opening which depends on the diameter of the objective len or mirror; useful magnification = 60 X for each inch of diameter)

Review 4 • There are two kinds of telescopes: – refracting (2 lenses) – reflecting (primary mirror, secondary mirror, and lens). • There are three basic kinds of reflecting telescopes: – Prime focus (no secondary mirror) – Newtonian focus (uses secondary mirror to reflect the light out the side of the telescope) – Cassegrainian focus (uses secondary mirror to reflect light out the back of the telescope)
- Slides: 75