Properties Power Rule Exponential Equations Equations with variables


Properties • Power Rule:

Exponential Equations • Equations with variables in the exponents are called Exponential Equations • For simple equation, use the followingprinciple:

Solving simple equations These exponential equations are simple because we can express both sides of the equations as a power of the same base

Solving exponential equation Take the natural logarithm on both sides Use Power Rule Divide both sides by ln 2 This is the exact solution Use calculator to find the approximate solution

Strategies for Solving Exponential Equations 1. Isolate the exponential term 2. Take the natural logarithm on both sides 3. Use the power rule to pull the x out of the exponent 4. Solve the resulting equation 5. Check the answer in the original equation.

Example Solve: e 1. 32 t – 2000 =0 Solution We have: e 1. 32 t = 2000 ln e 1. 32 t = ln 2000 Take the natural logarithm 1. 32 t = ln 2000 t = (ln 2000)/1. 32

Example Solve: 3 x +1 – 43 = 0 Solution We have 3 x +1 = 43 log 3 x +1 = log 43 (x +1)log 3 = log 43 Power rule for logs x +1 = log 43/log 3 x = (log 43/log 3) – 1 The solution is (log 43/log 3) – 1, or approximately 2. 4236.
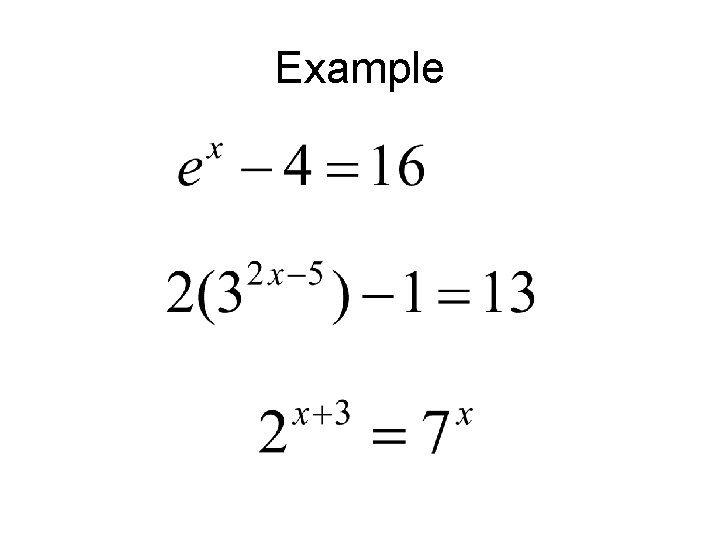
Example
http: //www. intmath. com/Exponential-logarithmic-functions/6_Logarithmexponential-eqns. php The above link is a good website to learn new concept. It has many applications.

World Population • The world population in billions at time t, where t = 0 represents the year 2000, is given by: • When will the population reach 12 billions?

Strategies for solving Logarithmic Equations 1. 2. 3. 4. 5. Move all logarithms to left hand side (LHS) Write the LHS as a single logarithm Rewrite the equation in exponential form Solve the resulting equation Check the answer in the original equation.

Example Solve: log 2(6 x + 5) = 4. Solution log 2(6 x + 5) = 4 6 x + 5 = 24 6 x + 5 = 16 6 x = 11/6 Check the solution!

Example Solve: log x + log (x + 9) = 1. Solution log x + log (x + 9) = 1 log[x(x + 9)] = 1 x(x + 9) = 101 x 2 + 9 x = 10 x 2 + 9 x – 10 = 0 (x – 1)(x + 10) = 0 x – 1 = 0 or x + 10 = 0 x = 1 or x = – 10

Check x = 1: x = – 10: log 1 + log (1 + 9) 0 + log (10) 0+1 =1 TRUE log (– 10) + log (– 10 + 9) FALSE The logarithm of a negative number is undefined. The solution is 1.

Example Solve: log 3(2 x + 3) – log 3(x – 1) = 2. Solution log 3(2 x + 3) – log 3(x – 1) = 2 log 3[(2 x + 3)/(x – 1)] = 2 (2 x + 3)/(x – 1) = 32 (2 x + 3)/(x – 1) = 9 (2 x + 3) = 9(x – 1) 2 x + 3 = 9 x – 9 x = 12/7 Check the solution!
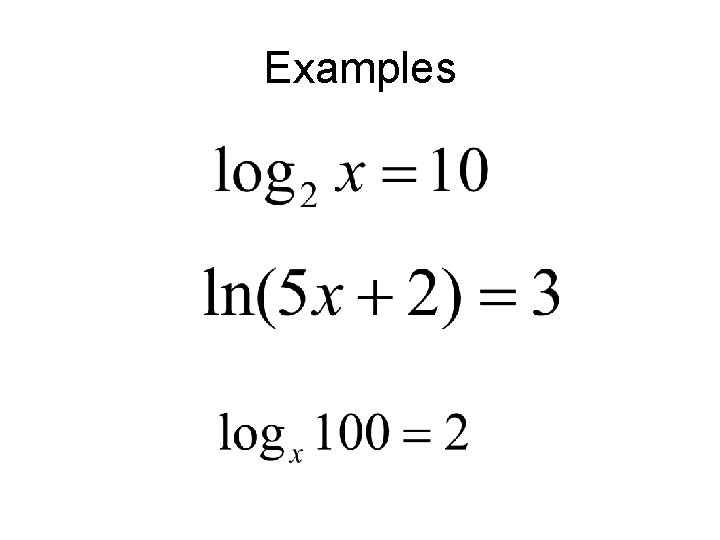
Examples
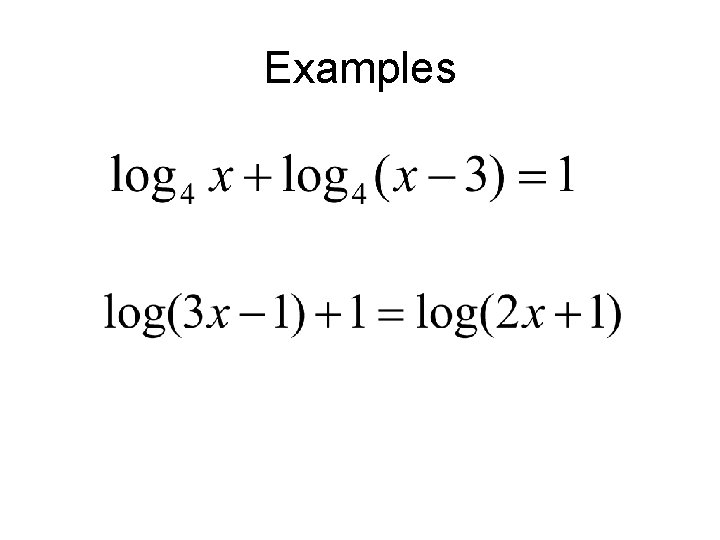
Examples
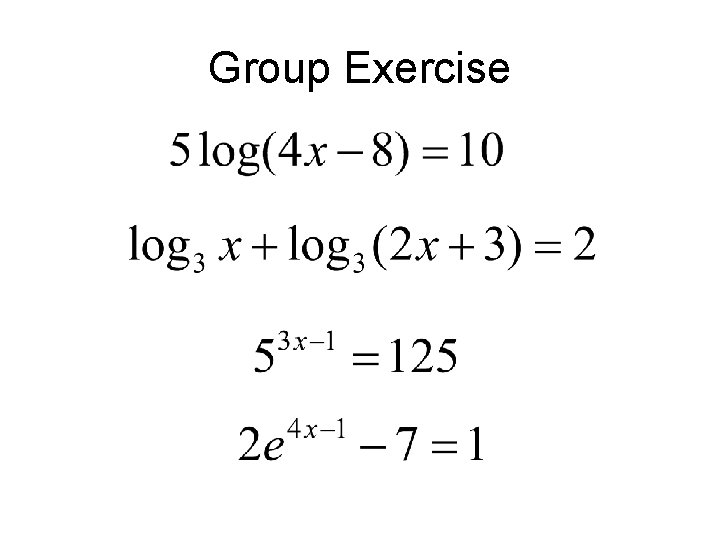
Group Exercise
- Slides: 19