Properties of Pure Substance Chapter 3 PVT Behavior

Properties of Pure Substance Chapter 3 PVT Behavior of Pure Substance, The Steam Table, Equations of State, The Ideal Gas, Virial Equations of State, Application of the Virial Equations, Theorem of the Corresponding State and the Generalized Correlations

Pure Substance ¬ Pure substance is a substance that has a homogeneous and invariable chemical composition It may exists in different phases (l, v, s), but always keep the same composition in all phases Example: Pure substance liquid water, mixture of liquid water + water vapor, mixture of ice + liquid water. Example: Humid air is Not a pure substance Mixture of air + gaseous air (why? ) Vap. Air Liq. Air Chemical Engineering Dept. BUE Composition of liquid phase is not the same as that of the vapor phase Eng. Thermodynamics 3 -2

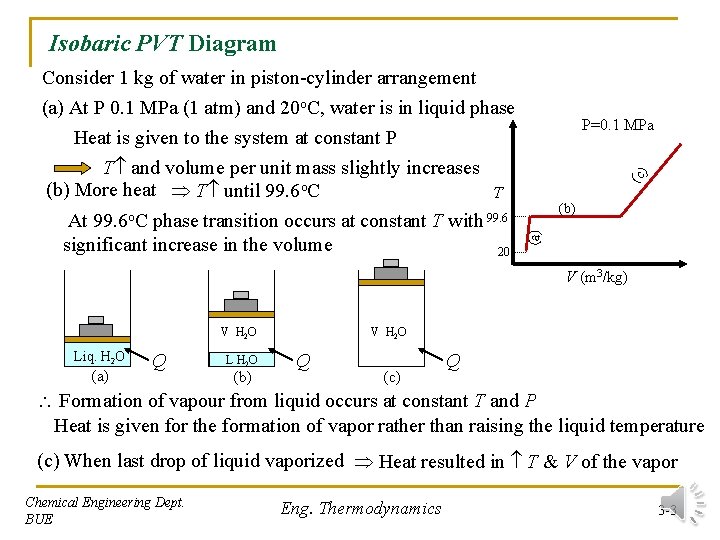
Isobaric PVT Diagram (c ) P=0. 1 MPa (b) (a) Consider 1 kg of water in piston-cylinder arrangement (a) At P 0. 1 MPa (1 atm) and 20 o. C, water is in liquid phase Heat is given to the system at constant P T and volume per unit mass slightly increases (b) More heat T until 99. 6 o. C T At 99. 6 o. C phase transition occurs at constant T with 99. 6 significant increase in the volume 20 V (m 3/kg) V H 2 O Liq. H 2 O (a) Q L H 2 O (b) V H 2 O Q (c) Q Formation of vapour from liquid occurs at constant T and P Heat is given for the formation of vapor rather than raising the liquid temperature (c) When last drop of liquid vaporized Heat resulted in T & V of the vapor Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -3

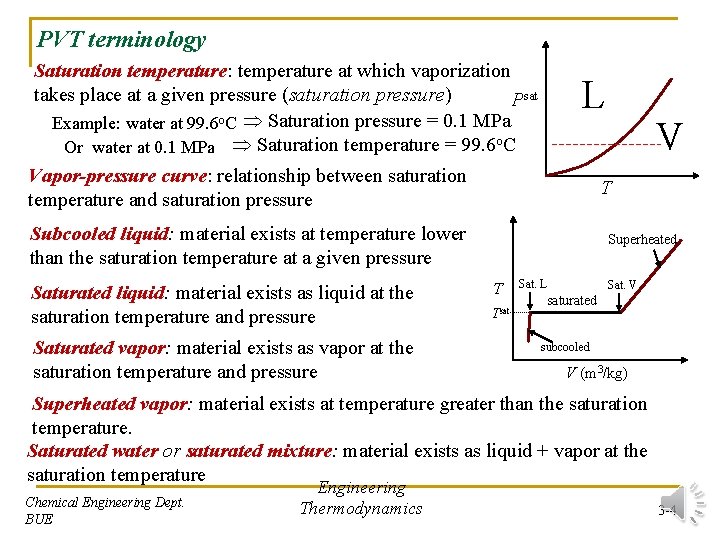
PVT terminology Saturation temperature: temperature at which vaporization takes place at a given pressure (saturation pressure) Psat Example: water at 99. 6 o. C Saturation pressure = 0. 1 MPa Or water at 0. 1 MPa Saturation temperature = 99. 6 o. C L Vapor-pressure curve: relationship between saturation temperature and saturation pressure T Subcooled liquid: material exists at temperature lower than the saturation temperature at a given pressure Saturated liquid: material exists as liquid at the saturation temperature and pressure Saturated vapor: material exists as vapor at the saturation temperature and pressure V Superheated T Tsat Sat. L Sat. V saturated subcooled V (m 3/kg) Superheated vapor: material exists at temperature greater than the saturation temperature. Saturated water or saturated mixture: material exists as liquid + vapor at the saturation temperature Chemical Engineering Dept. BUE Engineering Thermodynamics 3 -4

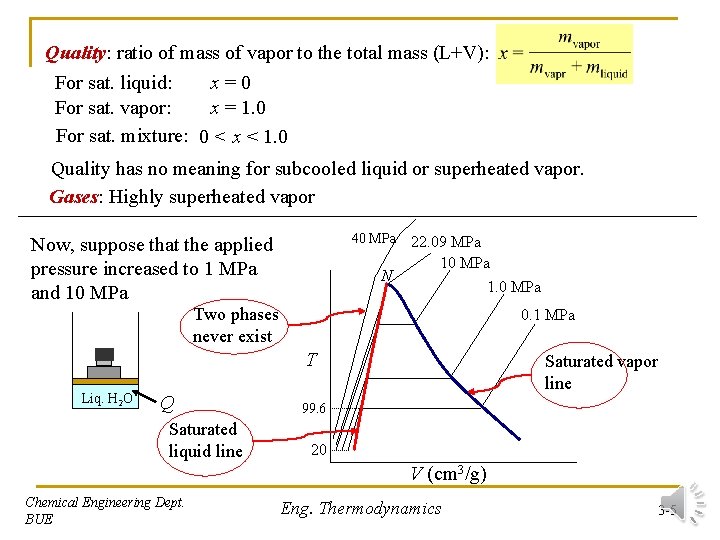
Quality: ratio of mass of vapor to the total mass (L+V): For sat. liquid: x=0 For sat. vapor: x = 1. 0 For sat. mixture: 0 < x < 1. 0 Quality has no meaning for subcooled liquid or superheated vapor. Gases: Highly superheated vapor 40 MPa Now, suppose that the applied pressure increased to 1 MPa and 10 MPa N 22. 09 MPa 10 MPa 1. 0 MPa Two phases never exist 0. 1 MPa T Liq. H 2 O Q Saturated liquid line Saturated vapor line 99. 6 20 V (cm 3/g) Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -5

Critical Behavior Critical point (N): the point where the saturated liquid and saturated vapor become identical (the two phases become indistinguishable) • Each material has its own critical point which is characterized by: Pc: critical pressure Tc: critical temperature Vc: critical volume • The critical point can be used to characterize each material from the other • Heating at pressure above the critical pressure results in only one phase, two phases together never exist; when it is liquid and when it is vapor is an invalid question. . . The material is just referred as FLUID. • Arbitrary speaking, if the material exists at temperature below the critical temperature and above the critical pressure, it is referred as compressed liquid. • Mathematically point N is an inflection point Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -6

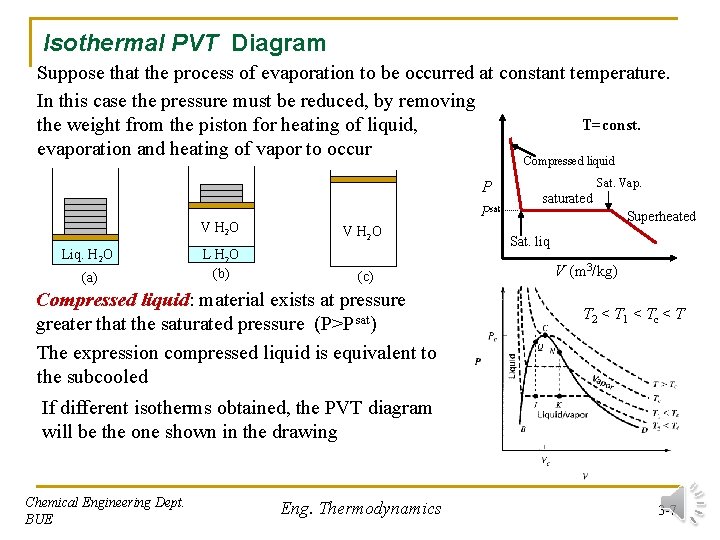
Isothermal PVT Diagram Suppose that the process of evaporation to be occurred at constant temperature. In this case the pressure must be reduced, by removing T=const. the weight from the piston for heating of liquid, evaporation and heating of vapor to occur Compressed liquid P Psat Liq. H 2 O (a) V H 2 O L H 2 O (b) (c) Compressed liquid: material exists at pressure greater that the saturated pressure (P>Psat) The expression compressed liquid is equivalent to the subcooled Sat. Vap. saturated Superheated Sat. liq V (m 3/kg) T 2 < T 1 < Tc < T If different isotherms obtained, the PVT diagram will be the one shown in the drawing Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -7

Fusion Process Suppose that the piston contains 1 kg ice at -20 o. C & 100 k. Pa (atmospheric) Heating T with slight in volume until T = 0 o. C Melting of ice at constant T During melting solid and liquid exits together at equilibrium; constant T and P Saturated solid: state of material at the beginning of melting, or fusion Saturated liquid: state of material at the end of melting, or fusion If P is higher temperature at which fusion occurs will be lower L Unusual behavior: During melting, for most substances the specific volume increases; but it is only for water the specific volume of liquid phase is less than the specific volume of solid phase. P P-T diagram for the fusion process S T When all of the ice melts heating would be used for increasing liquid temperature Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -8

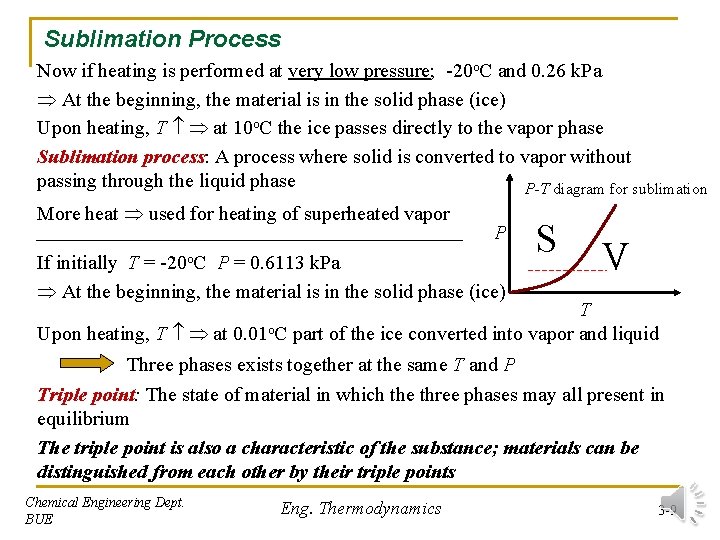
Sublimation Process Now if heating is performed at very low pressure; -20 o. C and 0. 26 k. Pa At the beginning, the material is in the solid phase (ice) Upon heating, T at 10 o. C the ice passes directly to the vapor phase Sublimation process: A process where solid is converted to vapor without passing through the liquid phase P-T diagram for sublimation More heat used for heating of superheated vapor -20 o. C P If initially T = P = 0. 6113 k. Pa At the beginning, the material is in the solid phase (ice) S V T Upon heating, T at 0. 01 o. C part of the ice converted into vapor and liquid Three phases exists together at the same T and P Triple point: The state of material in which the three phases may all present in equilibrium The triple point is also a characteristic of the substance; materials can be distinguished from each other by their triple points Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -9

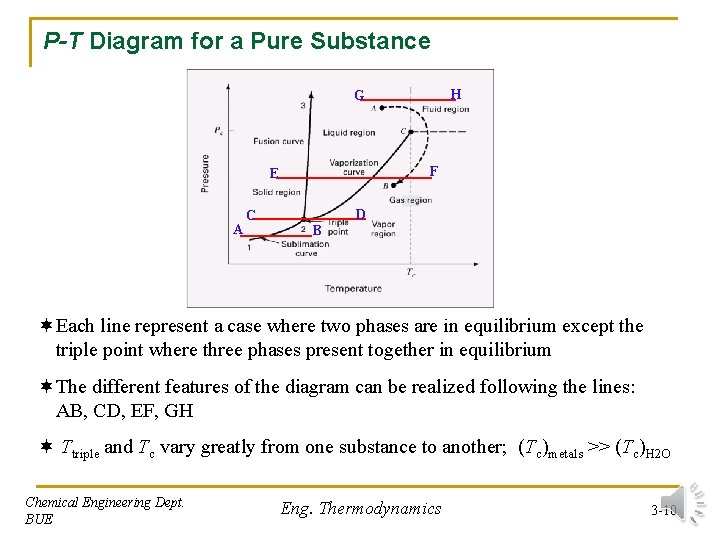
P-T Diagram for a Pure Substance H G F E A C D B ¬Each line represent a case where two phases are in equilibrium except the triple point where three phases present together in equilibrium ¬The different features of the diagram can be realized following the lines: AB, CD, EF, GH ¬ Ttriple and Tc vary greatly from one substance to another; (Tc)metals >> (Tc)H 2 O Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -10

Tables of Thermodynamic Properties: Steam Thermodynamic Tables: give temperature, pressure, volume, enthalpy, internal tables energy, and entropy in tables Table F. 1 (Page 716): gives properties of saturated steam (water) • 1 st and 2 nd columns represent Tsat in o. C and K, respectively. • 3 rd column represents the corresponding saturated pressure, Psat (kpa) • 4 th column: specific volume of saturated liquid, Vl (cm 3/g), at Tsat • 6 th column: specific volume of saturated vapor, Vv (cm 3/g), at the same Tsat • 5 th column: Vv – Vl = Vlv (cm 3/g), at the same Tsat • Next three columns: represent Ul, Ulv , and Uv (k. J/kg), at the same Tsat • Next three columns: represent Hl, Hlv , and Hv (k. J/kg), at the same Tsat According to the degrees of freedom, only one state variable (normally either Tsat or Psat) needs to be specified for the two phase region in order determine all othermodynamic properties Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -11

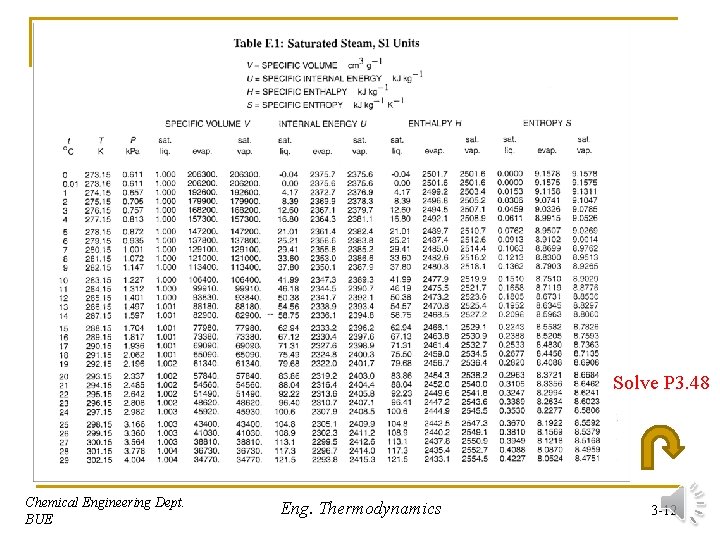
Solve P 3. 48 Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -12

Specific volume of a substance in the two phase region The fraction of vapor and liquid vary within this region, thus the volume of the substance can be found if the quality is known: xl + xv = 1. 0 Let a mass of a substance to be 1 kg having a quality xv, then: and Specific volume of the substance would be: Or Re-arrange Define: Similarly, the internal energy and enthalpy of saturated mixture can be given by: Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -13

Example: A vessel having a volume of 0. 4 m 3 contains 2 kg of a liquid water and water vapor mixture in equilibrium at a pressure of 0. 6 MPa, determine: 1. The corresponding saturated temperature, 2. The volume and mass of liquid, and 3. The volume and mass of vapor. Chemical Engineering Dept. BUE Eng. Thermodynamics m = 2 kg V = 0. 4 m 3 P = 0. 6 Pa V L 3 -14

Superheated vapor According to the degrees of freedom, for superheated vapor: = 1; N = 1; F=2 - +N=2– 1+1=2 Two variables must be fixed in order to determine the intensive state of the system, or in order to determine all othermodynamic properties. Normally these are temperature (T) and pressure (P). Table F. 2 (Page 722): gives properties of superheated steam (water) For each P, large set of temperatures are given for determination of thermodynamic properties Tables are also available, in other texts, for compressed liquid (at different T and P) and for saturated solids to determine thermodynamic properties Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -15

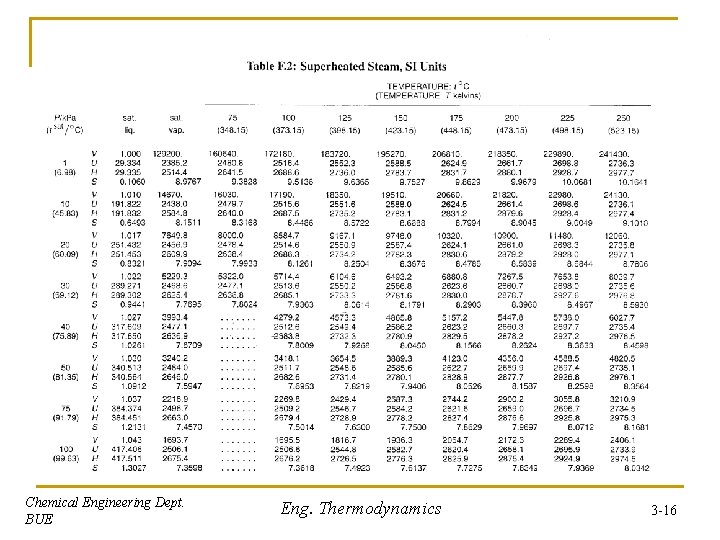
Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -16

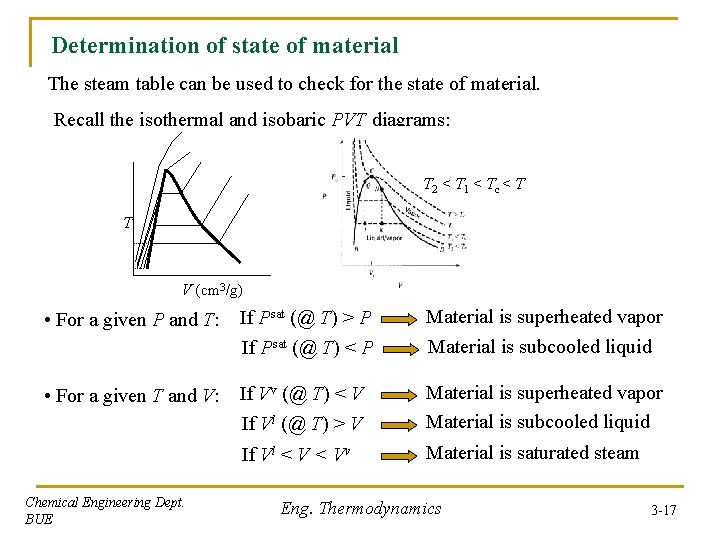
Determination of state of material The steam table can be used to check for the state of material. Recall the isothermal and isobaric PVT diagrams: T 2 < T 1 < Tc < T T V (cm 3/g) • For a given P and T: If Psat (@ T) > P If Psat (@ T) < P Material is superheated vapor Material is subcooled liquid • For a given T and V: If Vv (@ T) < V If Vl (@ T) > V Material is superheated vapor Material is subcooled liquid If Vl < Vv Chemical Engineering Dept. BUE Material is saturated steam Eng. Thermodynamics 3 -17

Example: Determine whether water at each of the following states is compressed liquid, a superheated vapor or a mixture of saturated liquid and saturated vapor: (a) T = 120 o. C & P = 150 k. Pa Get Psat and compare with P (b) P = 0. 3 MPa & V = 400 cm 3/g Get Vl and Vv compare with V (c) T = 160 o. C & V = 400 cm 3/g (d) T = 110 o. C & P = 200 k. Pa (e) T = 300 o. C & V = 10 cm 3/g (f) T = 10 o. C & P = 5 k. Pa Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -18

Equations of State (EOS) ¬ The phase diagram showed that T, P and V of any pure material are related to each other. This can mathematically be expressed as: f(T, P, V) = 0 Equation of State (EOS) ¬ The simplest EOS is the one ideal gas, expressed as: PV = RT This equation was derived for real gases at very low pressures and is applied for a wide number of gases and vapors ( up to 5 atm). ¬ Most gases do not follow the ideal gas equation of state and, thus, more complicated forms are required. Assumptions of the Ideal Gas EOS 1. Gas molecules are infinitesimal spheres which occupy no volume. 2. The molecules undergo completely elastic collisions with each others and with the walls of the container 3. No intermolecular attraction or repulsion occurs between the gas molecules. Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -19

Ideal and Real Liquids The other form of the equation f(T, P, V) = 0 is: V = V(T, P) We can write: Define the following: 1. Volume expansivity: 2. Isothermal compressibility: Isotherms for liquid on the left side are very steep and closely spaced, this results in: T 2 < T 1 < Tc < T = =0 Idealization for liquids Incompressible liquid Real fluids, or liquids, are not compressible, in reality no real fluid is truly incompressible. There is no EOS for incompressible fluids Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -20

For real liquids, and are very weak functions of T and P. Thus, for small changes in T and P, small error is introduced if we regard them as constant: (approximation for real liquids) (Read Example 3. 1, Page 69 - Textbook) Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -21

The Van der Waals EOS ¬Number of equations have been derived for the modification of the ideal gas to real gas ¬ Application of these equations depends on the accuracy required ¬Van der Waals equation was derived to consider the two worst assumptions of the ideal gas; infinitesimal molecular size and no intermolecular forces. Volume of the container; does not consider molecular volume Modification on P for the intermolecular forces PV = RT Not real pressure; it does not consider the intermolecular forces Modification on V for the molecular size P V = RT b: called molecular volume, is a parameter to account for the finite size of the gas molecules a/V 2: to account for the attractive forces existing between the molecules Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -22

Virial EOS Limitation of Van der Waals EOS: 1. Not accurate at the critical point 2. Not good for liquids 3. Not good for vapor Virial is a polynomial Taylor series form: Or: where: B’ = b/a , C’ = c/a …. . a, B’, C’ … are constants for a given temperature and given chemical species B’, C’, …. = f(T, species) ¬RHS of virial equation is an infinite series, but in practice only finite number of terms are considered ¬At low to moderate pressures, the series is truncated after the second or third terms (referred as 2 nd or 3 rd order virial EOS) Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -23

Limiting behavior of virial EOS Shown in the drawing a plot of PV vs. P for four gases at the triple-point temperature water For all gases: According to virial, as P 0: (PV)* = a = f(T) This dependency should be the same for all gases To make a identical for all gases, the functionality f(T) should be also the same. (PV)* T Or PV = RT R is proportionality constant ¬As P 0, individual molecules becomes more widely separated. The volume of the molecules themselves becomes smaller and only small fraction of the total volume occupied by the gas. Moreover, the forces of attraction between molecules become ever smaller because of the increasing distance between the molecules. Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -24

In the limit, as P 0 infinite distance between molecules such that the molecular volume becomes negligible compared to the total volume and intermolecular forces will be zero. At these conditions, all gases are said to be ideal and the previous equation is known as ideal-gas EOS and R is called universal idea-gas constant. ¬ Since a = RT, the virial equation can be expressed as: Or: Where Z: compressibility factor Alternative expression of the virial equation in terms of volume: 1 st virial 3 rd virial th Coeff. 2 nd virial Coeffic. 4 virial coefficient Coeffic. Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -25

B’, C’, D’, …… & B, C, D…. are called virial coefficients. B’ or B: second virial coefficient C’ or C: third virial coefficient etc…. ¬Many other equations are also available, but virial equations are the only ones having a firm basis theory and provide physical significance of the virial coefficients, for example: account for the interaction between two molecules, account for three body interactions, etc… Statistically, 2 -body interactions are more probable than 3 -body interactions, and 3 -body interactions is more probable than 4 -body interactions, …etc. Contribution of Z to higher order terms decreases rapidly. Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -26

Ideal gas Consequently, if there is no molecular interactions Virial expression becomes: Z=1 B/V = C/V 2, … = 0 or PV = RT For real gases, molecular interactions do exist and Z will be different than 1. P (at constant T) V increased less contributions of the terms B/V, C/V 2, …. etc In the limit: P 0 Z 1. 0 & V Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -27

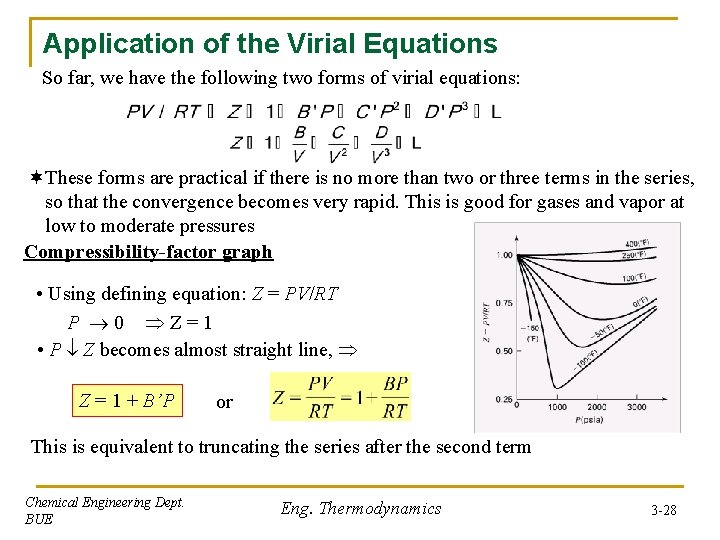
Application of the Virial Equations So far, we have the following two forms of virial equations: ¬These forms are practical if there is no more than two or three terms in the series, so that the convergence becomes very rapid. This is good for gases and vapor at low to moderate pressures Compressibility-factor graph • Using defining equation: Z = PV/RT P 0 Z = 1 • P Z becomes almost straight line, Z = 1 + B’P or This is equivalent to truncating the series after the second term Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -28

At low to moderate pressure, second order virial equation can be written as: These approximations are good for low pressures up to 15 bar. ü Remember that B depends on the nature of gas and temperature üB can be measured experimentally ¬ For 15 < P < 50 bar, three terms virial truncation is obviously more accurate: • Cubic in volume • solved for V by iterations (trial and error) • referred as cubic equation N 2 Chemical Engineering Dept. BUE • Again C and B depend on the gas and temperature Similar trend can be observed for other gases Eng. Thermodynamics 3 -29

Example 3. 8: Reported values for the virial coefficients of isopropanol vapor at 200 o. C are B = -388 cm 3/mol and C = -26, 000 cm 3/mol 2. Calculate V and Z for isopropanol vapor at 200 o. C and 10 bar by: (a) The ideal-gas equation (b) Using the equation (c) Using the equation (d) Calculate the percentage error of b and c in comparison with a Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -30

Equations for Process Calculations: Ideal The Constant-Temperature (Isothermal) Process: Gases For non-flow process of an ideal gas at constant T: U = 0 First law becomes: or For isothermal non-flow involving ideal gas The Reversible Adiabatic Process: Adiabatic: Q = 0 For ideal gas: (No net heat transfer between system and surrounding) or or Re-arrange: Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -31

Define: Since CP – CV = R Integration gives For mechanically reversible adiabatic process involving an ideal gas with constant CP and CV or From ideal gas law: From the previous equations: or Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -32

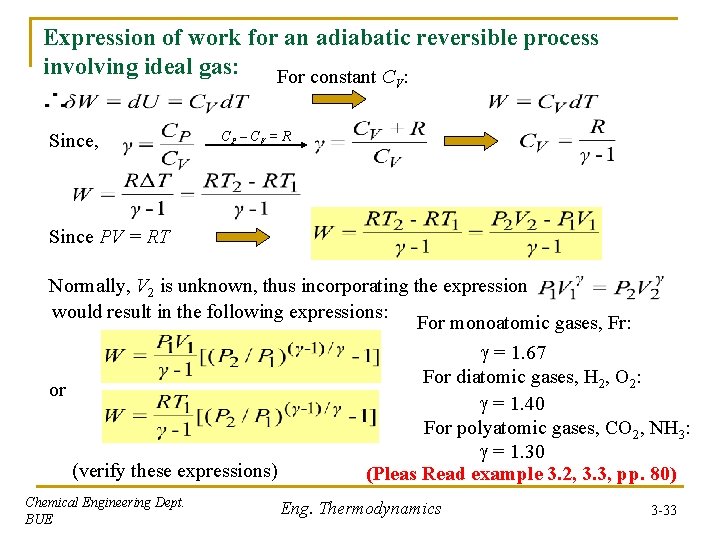
Expression of work for an adiabatic reversible process involving ideal gas: For constant C : V Since, CP – CV = R Since PV = RT Normally, V 2 is unknown, thus incorporating the expression would result in the following expressions: For monoatomic gases, Fr: = 1. 67 For diatomic gases, H 2, O 2: or = 1. 40 For polyatomic gases, CO 2, NH 3: = 1. 30 (verify these expressions) (Pleas Read example 3. 2, 3. 3, pp. 80) Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -33

Cubic Equations of state n van der Waals EOS (1873): n Redlich-Kwong EOS (1949): n Soave EOS (1972): n Peng-Robinson EOS (1976)

Cubic Equations of state (cont. ) Iterative procedures are often used to solve cubic EOS. Different procedures are followed for calculating vapor volumes or liquid volumes. How you can we determine the constants a & b Suitable estimates using critical constants of substance. Horizontal inflection at the critical point means that: Differentiation of the above cubic EOS yields expressions for a & b: For Redlich-Kwong EOS:

Generalized correlations for gases The Redlich-Kwong EOS: is modified, by elimination of a & b to yield: This type of generalized EOS can be solved either by: Iterative solution: For an initial value of Z = 1, calculate h. Calculate a new value for Z Repeat until convergence. Graphical charts: Only Pc & Tc are needed to plot Z vs. Pr for different isotherms Tr. Chemical Engineering Dept. BUE

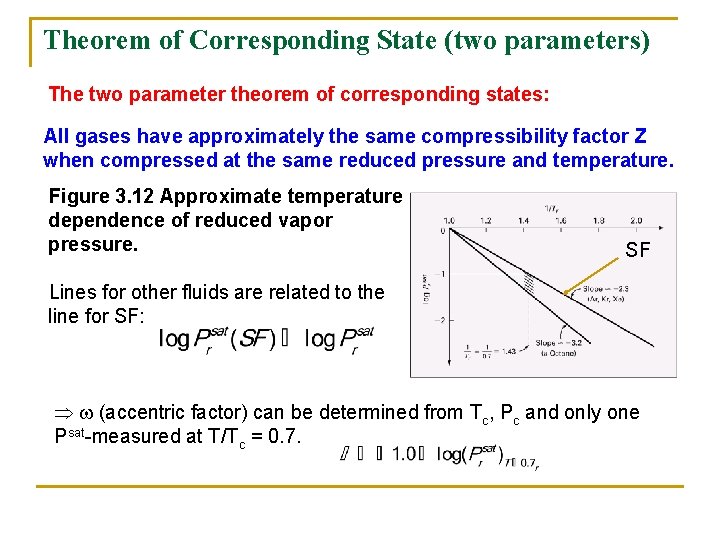
Theorem of Corresponding State (two parameters) The two parameter theorem of corresponding states: All gases have approximately the same compressibility factor Z when compressed at the same reduced pressure and temperature. Figure 3. 12 Approximate temperature dependence of reduced vapor pressure. SF Lines for other fluids are related to the line for SF: (accentric factor) can be determined from Tc, Pc and only one Psat-measured at T/Tc = 0. 7.

Theorem of Corresponding State (three Experimentally, it was found that Z for different materials is the same when parameters) correlated as function of Tr and Pr, where: & This leads to theorem of corresponding state: “All fluids, when compared at the same reduced temperature and pressure, have approximately the same compressibility factor and all deviate from ideal gas behavior about the same degree” Pitzer correlated Z in terms of three parameters Z 0, Z 1 and : Where is called accentric factor and is responsible for the molecular structure: And Z 0 & Z 1 = f(Tr, Pr) Tabulated at different Tr & Pr in PP. 695 -699 - , Tc, Pc, Vc, Zc for different materials are listed in Table B. 1, PP. 679 -681 Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -38

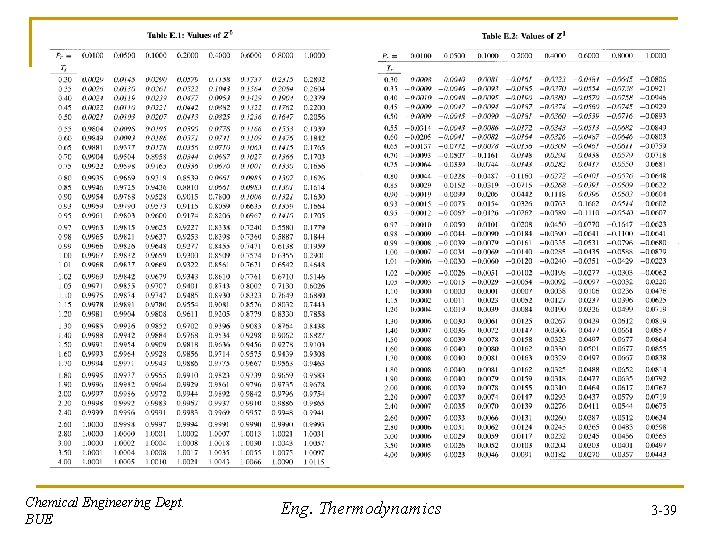
Chemical Engineering Dept. BUE Eng. Thermodynamics 3 -39

Generalized Virial Equation Virial equation in reduced form can be written as: Pitzer expressed the term BPc/RTc as: In this case, virial equation in its generalized form can be written as: Can be used for all materials Where: and: (Please read examples 3. 9 -3. 11 in Text-book) Chemical Engineering Dept. BUE Eng Thermodynamics 3 -40

Generalized correlations for liquids Correlation are available for estimating molar volumes of saturated liquids like the Rackett correlation: or alternatively : Another two-parameter corresponding states correlation (Lydersen, Greenkorn and Hougen) for estimating liquid volumes: Read from Fig. 3. 16 for a given Pr & Tr Chemical Engineering Dept. BUE

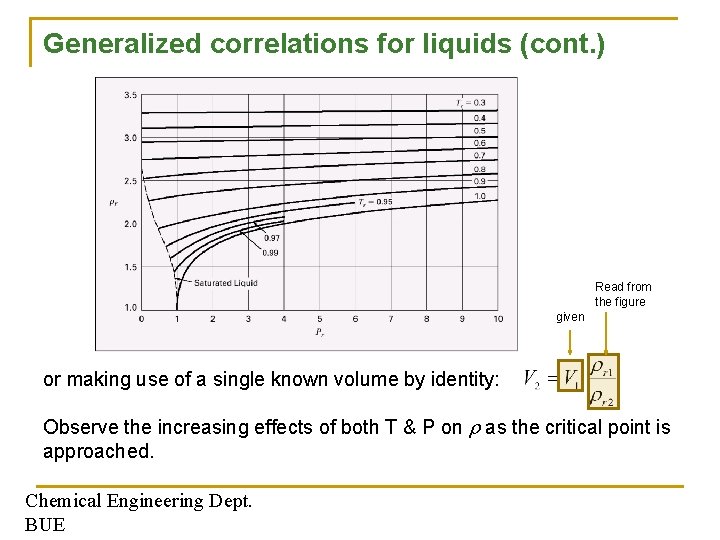
Generalized correlations for liquids (cont. ) Read from the figure given or making use of a single known volume by identity: Observe the increasing effects of both T & P on as the critical point is approached. Chemical Engineering Dept. BUE

Assignment: Solve the following problems from your textbook: 3. 5 3. 10 3. 18 3. 41 Chemical Engineering Dept. BUE Eng Thermodynamics 3 -43

Solution (P 3. 48) n Calculate the specific volume (V): mwater=15 kg , Vtotal=0. 4 m 3 Specific volume = n Use Table F. 2 at 400 C, at page 751 to interpolate for the pressure: V 1=27. 057 V=26. 667 V 2=26. 408 P 1=9800 Chemical Engineering Dept. BUE P=? P 2=1000 Eng. Thermodynamics 3 -44

Problem 1: A cylinder fitted with a piston has a volume of 100, 000 cm 3 and contains 500 g of water at 399. 15 k. Pa. Heat is transferred to the water until the temperature is 300 o. C, while the pressure remains constant. (a) Sketch the process on the T-V diagram. (b) Determine the heat transfer and the work for this process. Chemical Engineering Dept. BUE Eng Thermodynamics 3 -45

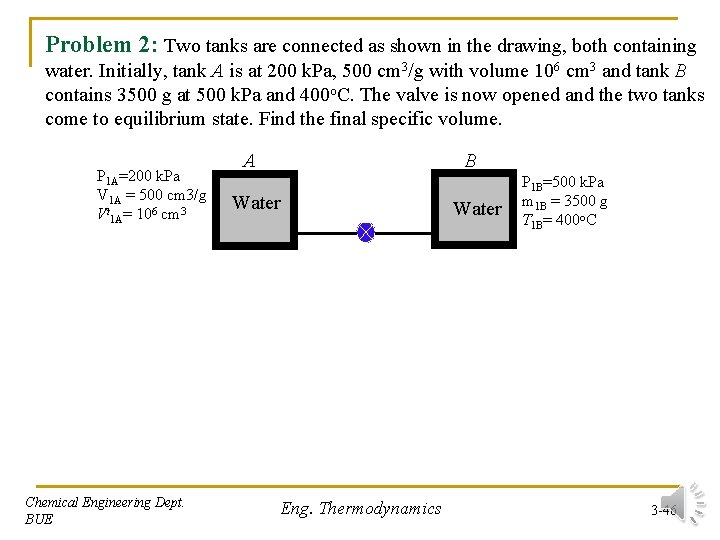
Problem 2: Two tanks are connected as shown in the drawing, both containing water. Initially, tank A is at 200 k. Pa, 500 cm 3/g with volume 106 cm 3 and tank B contains 3500 g at 500 k. Pa and 400 o. C. The valve is now opened and the two tanks come to equilibrium state. Find the final specific volume. P 1 A=200 k. Pa V 1 A = 500 cm 3/g Vt 1 A= 106 cm 3 Chemical Engineering Dept. BUE A B Water Eng. Thermodynamics Water P 1 B=500 k. Pa m 1 B = 3500 g T 1 B= 400 o. C 3 -46

Problem 3: A rigid vessel is divided into two room by a membrane, both containing an ideal gas with (CP/CV) = 1. 4, as shown in the drawing. Room A contains 1. 5 kmoles at 150 o. C, and room B contains 3. 5 kmoles at 400 o. C. The membrane now ruptures and heat transfer takes place so that gas comes to a uniform state at 100 o. C. Find the heat transfer during the process, in k. J. (Hint: U 1 = n. AUA + n. BUB) B A n 1 A = 1. 5 kmoles T 1 A = 150 o. C Chemical Engineering Dept. BUE n 1 B = 3. 5 kmoles T 1 B = 400 o. C Eng Thermodynamics 3 -47