PROPERTIES OF PARALLEL LINES POSTULATE 15 Corresponding Angles

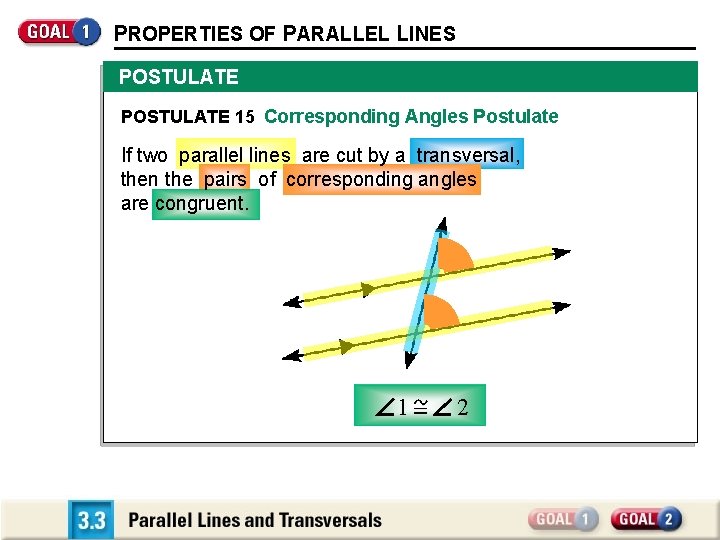
PROPERTIES OF PARALLEL LINES POSTULATE 15 Corresponding Angles Postulate If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent. 1 2

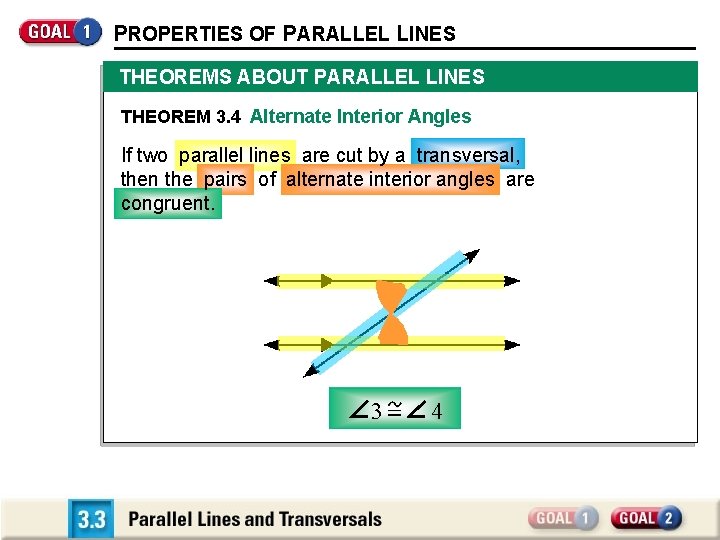
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 4 Alternate Interior Angles If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. 3 4

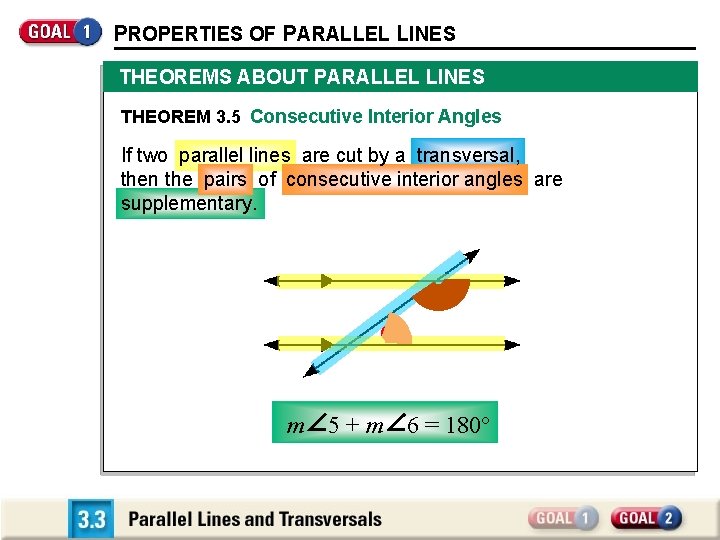
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 5 Consecutive Interior Angles If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary. 5 6 m 5+m 6 = 180°

PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 6 Alternate Exterior Angles If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent. 7 8

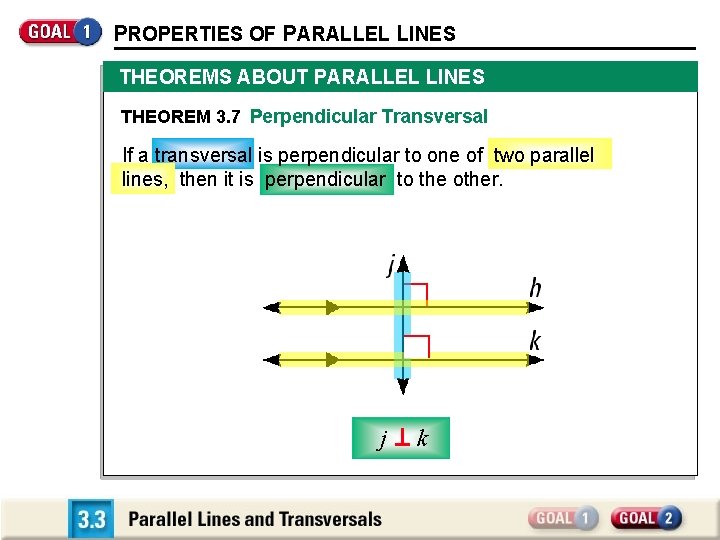
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 7 Perpendicular Transversal If a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other. j k

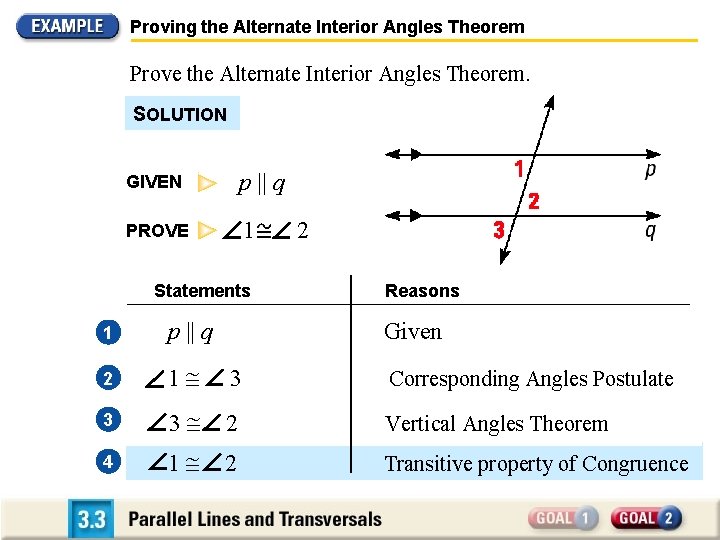
Proving the Alternate Interior Angles Theorem Prove the Alternate Interior Angles Theorem. SOLUTION GIVEN p || q PROVE 1 Statements 2 Reasons 1 p || q Given 2 1 3 Corresponding Angles Postulate 3 3 2 Vertical Angles Theorem 4 1 2 Transitive property of Congruence

Using Properties of Parallel Lines Given that m 5 = 65°, find each measure. Tell which postulate or theorem you use. SOLUTION m 6 = m 5 = 65° m 7 = 180° – m m 8 = m 5 = 65° Corresponding Angles Postulate m 9 = m 7 = 115° Alternate Exterior Angles Theorem Vertical Angles Theorem 5 = 115° Linear Pair Postulate

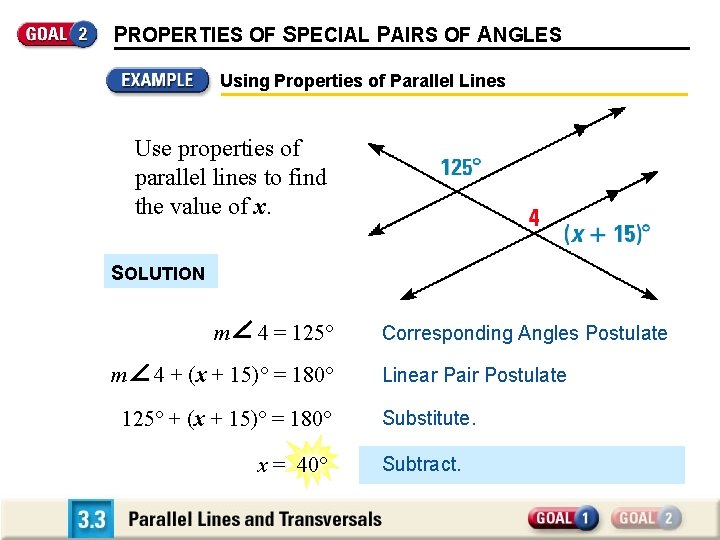
PROPERTIES OF SPECIAL PAIRS OF ANGLES Using Properties of Parallel Lines Use properties of parallel lines to find the value of x. SOLUTION m m 4 = 125° 4 + (x + 15)° = 180° 125° + (x + 15)° = 180° x = 40° Corresponding Angles Postulate Linear Pair Postulate Substitute. Subtract.

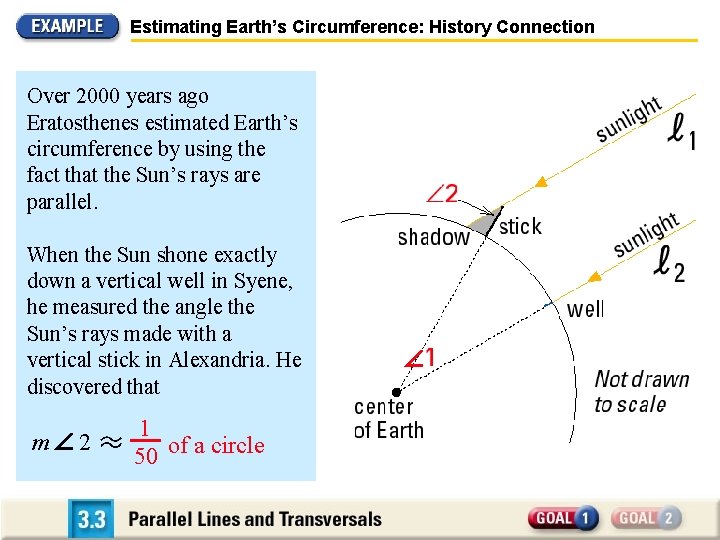
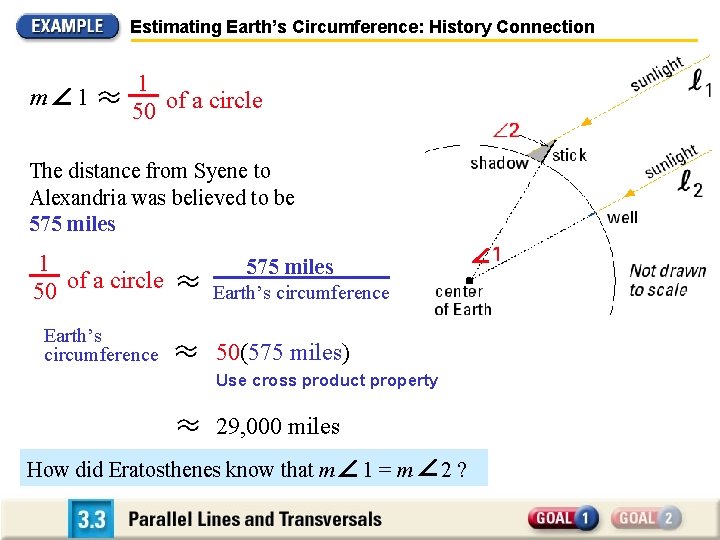
Estimating Earth’s Circumference: History Connection Over 2000 years ago Eratosthenes estimated Earth’s circumference by using the fact that the Sun’s rays are parallel. When the Sun shone exactly down a vertical well in Syene, he measured the angle the Sun’s rays made with a vertical stick in Alexandria. He discovered that m 2 1 50 of a circle

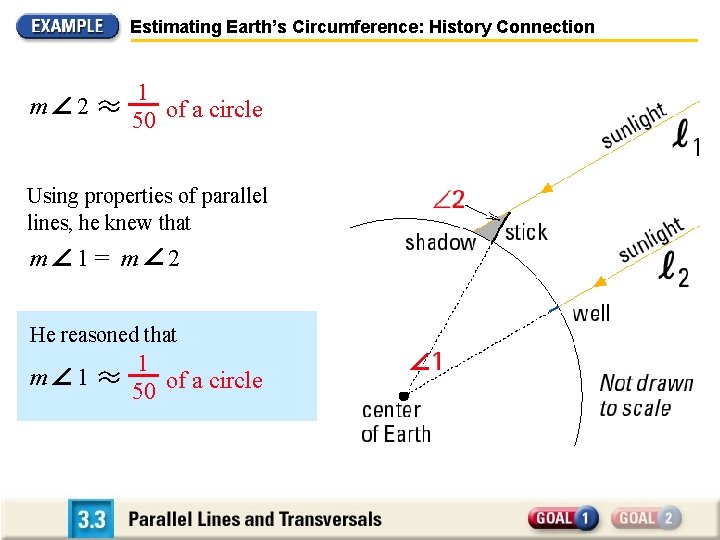
Estimating Earth’s Circumference: History Connection m 2 1 50 of a circle Using properties of parallel lines, he knew that m 1= m 2 He reasoned that m 1 1 50 of a circle

Estimating Earth’s Circumference: History Connection m 1 1 50 of a circle The distance from Syene to Alexandria was believed to be 575 miles 1 50 of a circle Earth’s circumference 575 miles Earth’s circumference 50(575 miles) Use cross product property 29, 000 miles How did Eratosthenes know that m 1=m 2?

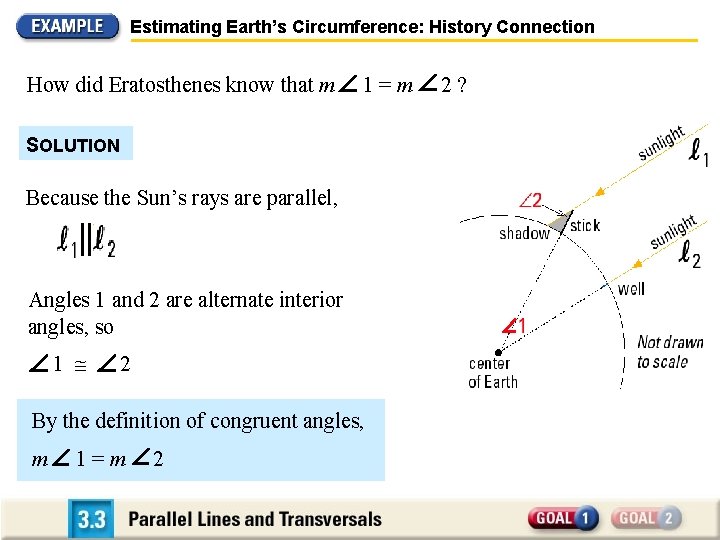
Estimating Earth’s Circumference: History Connection How did Eratosthenes know that m 1=m SOLUTION Because the Sun’s rays are parallel, Angles 1 and 2 are alternate interior angles, so 1 2 By the definition of congruent angles, m 1=m 2 2?