Properties of Musical Sound Subjective Objective Pitch Frequency

Properties of Musical Sound Subjective Objective Pitch Frequency Volume Amplitude/power/intensity Timbre Overtone content/spectrum Duration in beats Duration in time

Direct Sound waves that travel directly from the source to the listener. Direct Sound intensity attenuates with the distance according to the inverse square law. For example, doubling the distance will result in an attenuation of 4 times, or

Early (first order) Reflection Sound waves that travel to the listener after reflecting “once” from the environment (mainly walls). Early reflection within 35 ms from direct sound reinforce the latter. According to Beranek who study 54 concert halls, “intimate” effect was felt with early reflections of less than 20 ms. In large halls, suspended reflectors are employed to provide early reflection to center seats.

Reverberation (second to higher order reflection) Sound waves that travel to the listener after reflection of first-order-reflection. Reverberation will decay with time as sound energy is absorbed by the enviroment. Reverberation time is the duration for the sound pressure to drop to 60 d. B of its initial level, in general for the frequency range of 500 -1000 Hz, High frequency signals are absorbed more quickly in air than low ones, reverberation time is hence shorter.

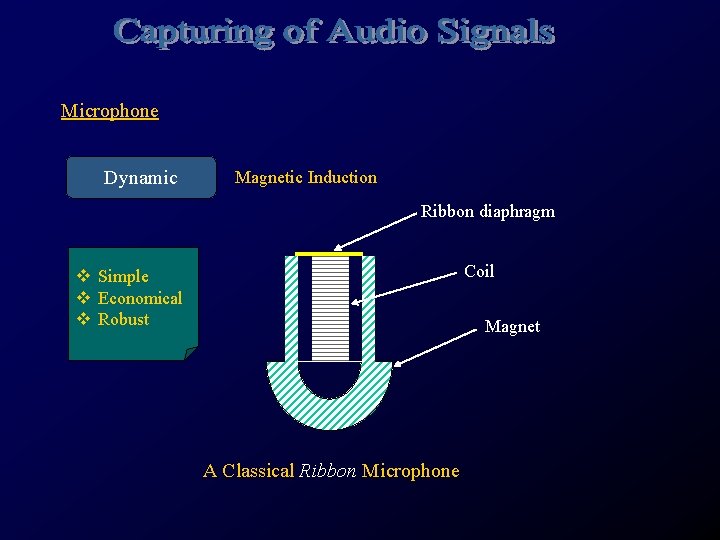
Microphone Dynamic Magnetic Induction Ribbon diaphragm Coil v Simple v Economical v Robust Magnet A Classical Ribbon Microphone

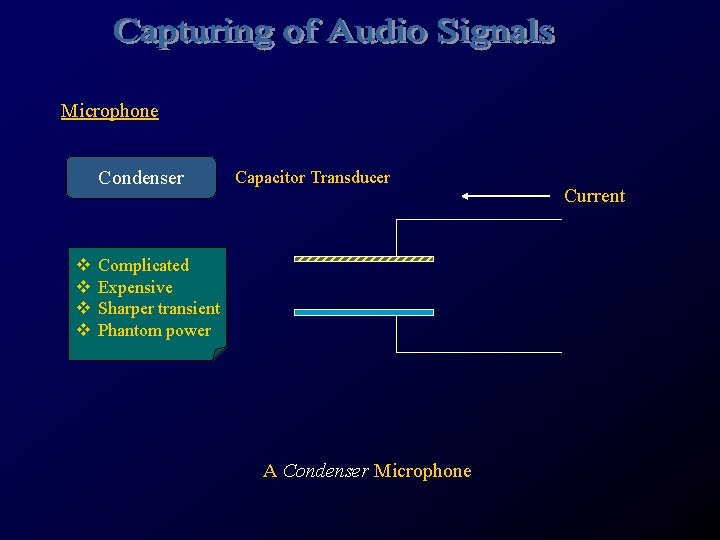
Microphone Condenser v v Capacitor Transducer Complicated Expensive Sharper transient Phantom power A Condenser Microphone Current

Magnitude of a microphone’s response to pressure changes imposed at different directions. 0 o 330 o 1. 0 30 o 0. 75 300 o 60 o 0. 50 0. 25 270 o 90 o 120 o 240 o 210 o 180 o 150 o

Omnidirectional 0 o 330 o 1. 0 30 o 0. 75 300 o 60 o 0. 50 0. 25 270 o 90 o 120 o 240 o 210 o 180 o 150 o

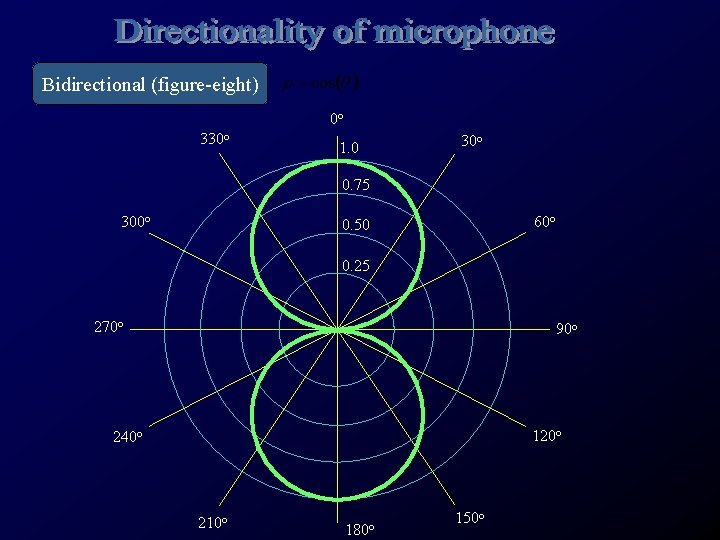
Bidirectional (figure-eight) 0 o 330 o 1. 0 30 o 0. 75 300 o 60 o 0. 50 0. 25 270 o 90 o 120 o 240 o 210 o 180 o 150 o

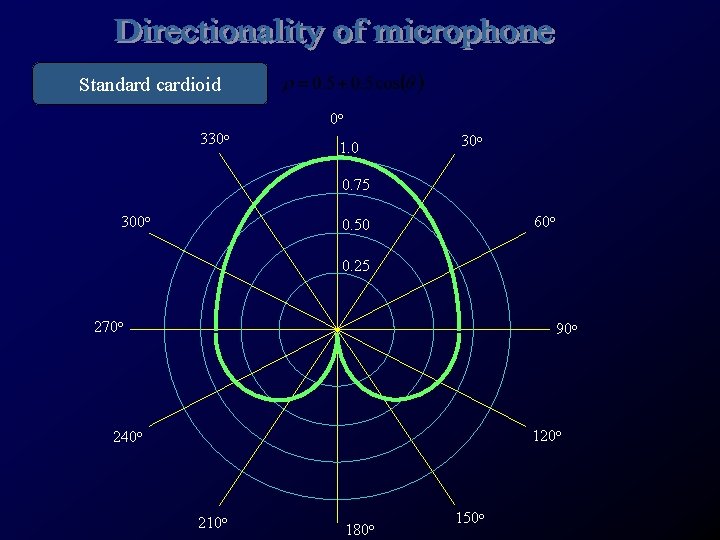
Standard cardioid 0 o 330 o 1. 0 30 o 0. 75 300 o 60 o 0. 50 0. 25 270 o 90 o 120 o 240 o 210 o 180 o 150 o

Supercardioid 0 o 330 o 1. 0 30 o 0. 75 300 o 60 o 0. 50 0. 25 270 o 90 o 120 o 240 o 210 o 180 o 150 o

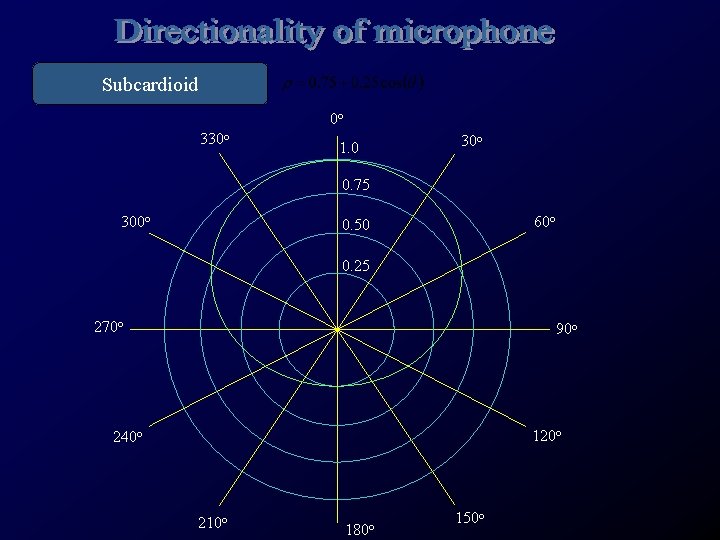
Subcardioid 0 o 330 o 1. 0 30 o 0. 75 300 o 60 o 0. 50 0. 25 270 o 90 o 120 o 240 o 210 o 180 o 150 o

XY (coincident pair) Microphone Recording 90 o-135 o Top view Front view Two identical cardioids aimed across each other at 90 o to 135 o, 12 inches or less apart Extremely mono-compatible, moderate stereo effect. Localization of sound source based on difference in amplitude. e. g. , if L > R, the source seems to be closer to the left side.

Blumlein coincident Microphone Recording 90 o Top view Front view Two identical “figure 8” microphones placed at 90 o, one directly on top of the other Create by Alan Blumlein, provides precise stereo imaging from sound sources at front and reverberation from rear. L R

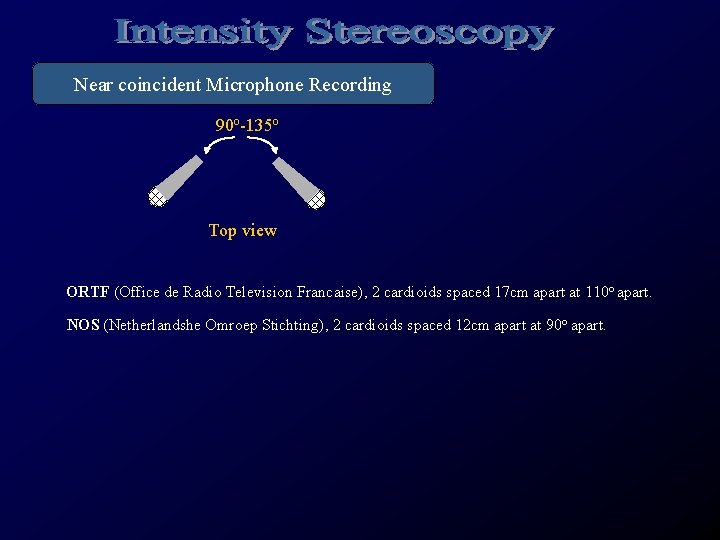
Near coincident Microphone Recording 90 o-135 o Top view ORTF (Office de Radio Television Francaise), 2 cardioids spaced 17 cm apart at 110 o apart. NOS (Netherlandshe Omroep Stichting), 2 cardioids spaced 12 cm apart at 90 o apart.

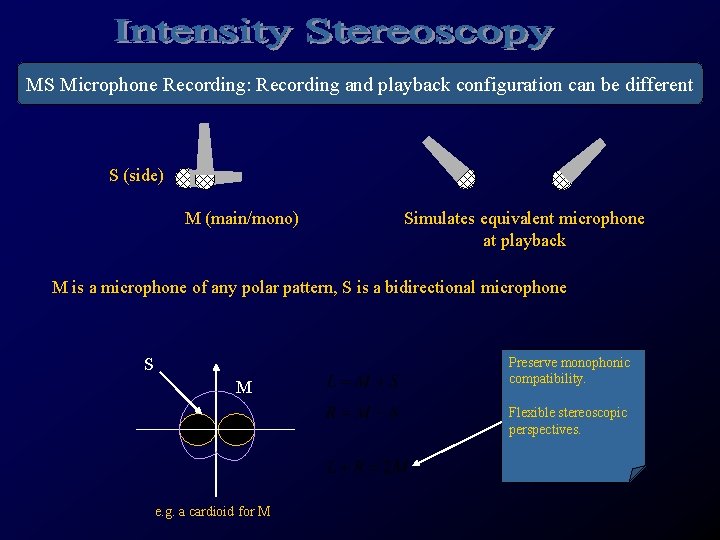
MS Microphone Recording: Recording and playback configuration can be different S (side) M (main/mono) Simulates equivalent microphone at playback M is a microphone of any polar pattern, S is a bidirectional microphone S M Preserve monophonic compatibility. Flexible stereoscopic perspectives. e. g. a cardioid for M

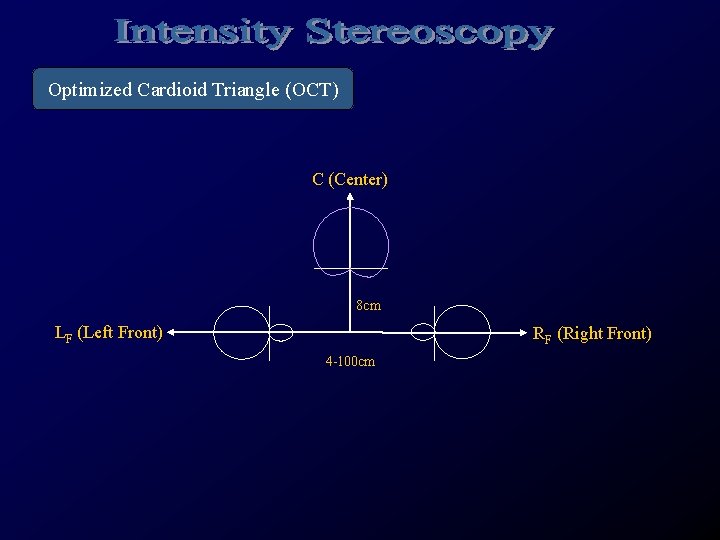
Optimized Cardioid Triangle (OCT) C (Center) 8 cm LF (Left Front) RF (Right Front) 4 -100 cm

INA 5 C (Center) L Ideale Nierenanordung (ideal cardioid) R 17. 5 cm Five cardioid microphones orientated in 5 directions to supply the five channels 17. 5 cm 60 o 60 cm LS 60 cm RS

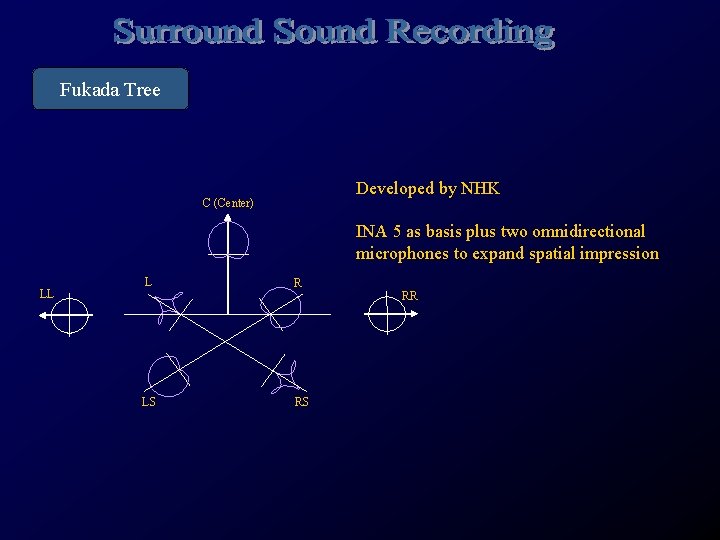
Fukada Tree Developed by NHK C (Center) INA 5 as basis plus two omnidirectional microphones to expand spatial impression LL L LS R RS RR

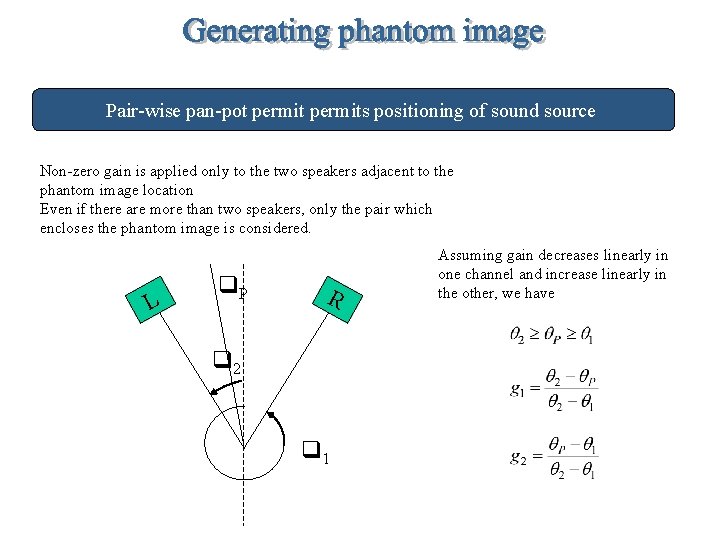
Pair-wise pan-pot permits positioning of sound source Non-zero gain is applied only to the two speakers adjacent to the phantom image location Even if there are more than two speakers, only the pair which encloses the phantom image is considered. L q. P R q 2 q 1 Assuming gain decreases linearly in one channel and increase linearly in the other, we have

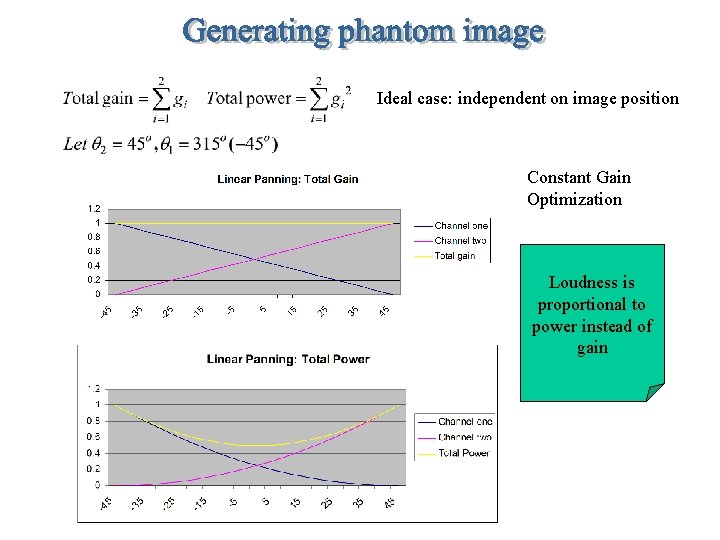
Ideal case: independent on image position Constant Gain Optimization Loudness is proportional to power instead of gain

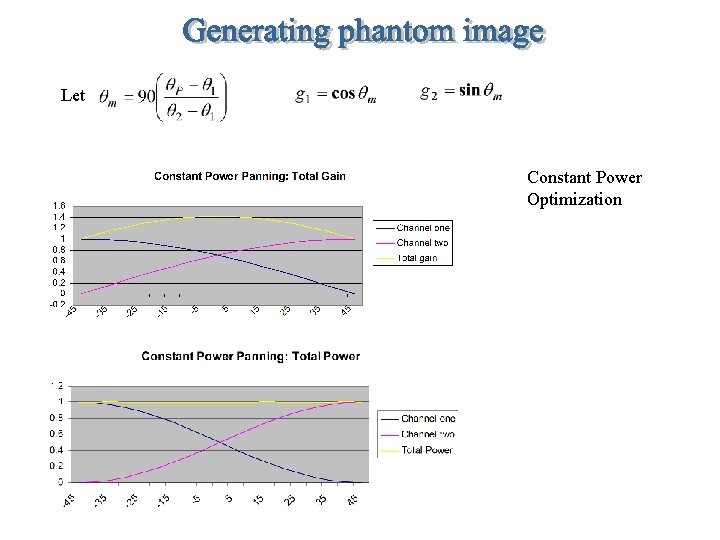
Let Constant Power Optimization

Time domain Digitization (e. g. CD) x(n) x(t) Sampling Quantization y(n) … 01001010. . . Bit-rate = Sampling rate (f) Bits per sample Number of Channels Example: bit-rate of 16 bits, 44 k. Hz stereo signal = 44, 100 16 2 = 1, 411, 200 bits per second = 176, 400 bytes per second

Time domain Digitization (e. g. CD) x(n) x(t) Sampling Quantization y(n) After sampling, the maximum frequency of the signal will be restricted to half the sampling frequency (why? ). The highest repetitive pattern that can be obtained with a sampling interval of T is shown below: 2 T Minimum period = T

2 T Minimum period = T A common convention: Normalized the digital frequencies to the range f w 0 0 fs/8 pi/4 fs/6 pi/3 fs/4 pi/2 fs/2 (fmax) pi

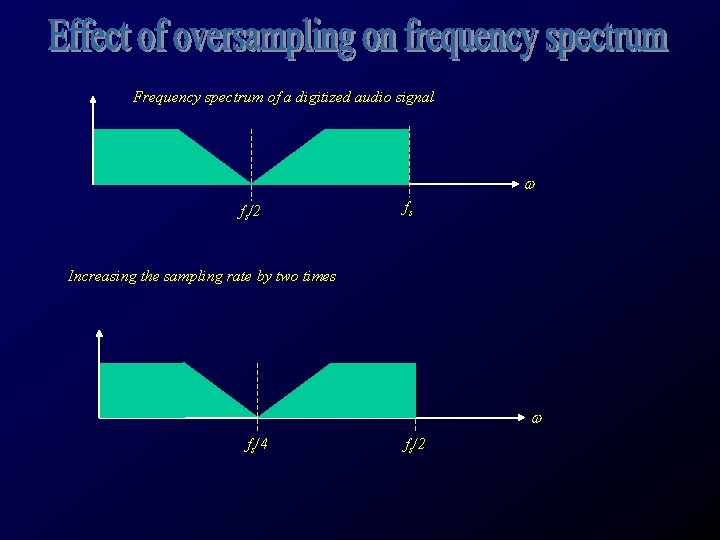
Frequency spectrum of a digitized audio signal w fs/2 fs Increasing the sampling rate by two times w fs/4 fs/2

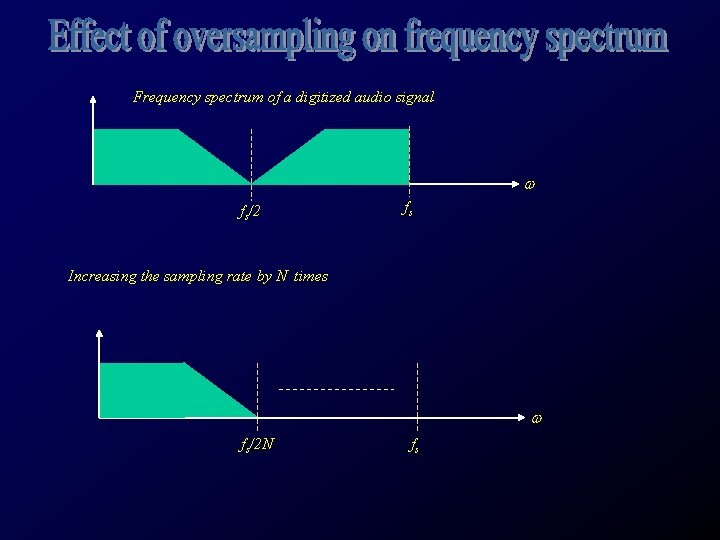
Frequency spectrum of a digitized audio signal w fs/2 fs Increasing the sampling rate by N times w fs/2 N fs

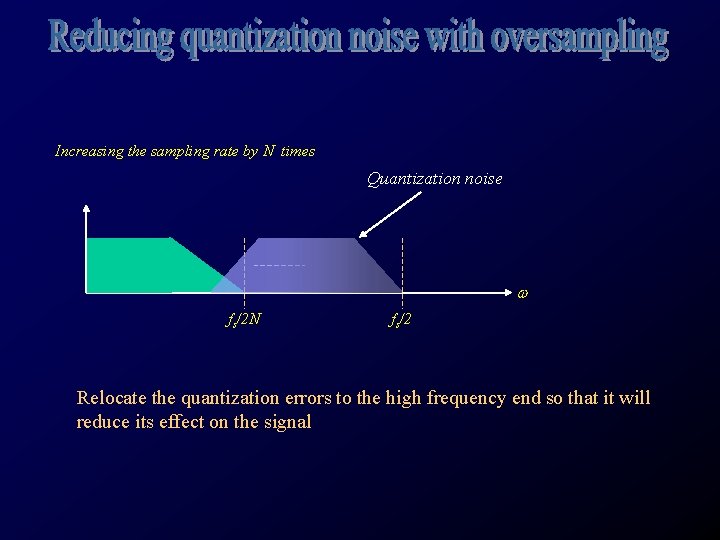
Increasing the sampling rate by N times Quantization noise w fs/2 N fs/2 Relocate the quantization errors to the high frequency end so that it will reduce its effect on the signal

q q/2 pk+1 pk If the signal is random (white) the probability distribution of the quantization noise is uniform, noise power (mean square quantization error) = Whenever q is reduced by two times, the power is reduced by 4, i. e. 6 d. B.

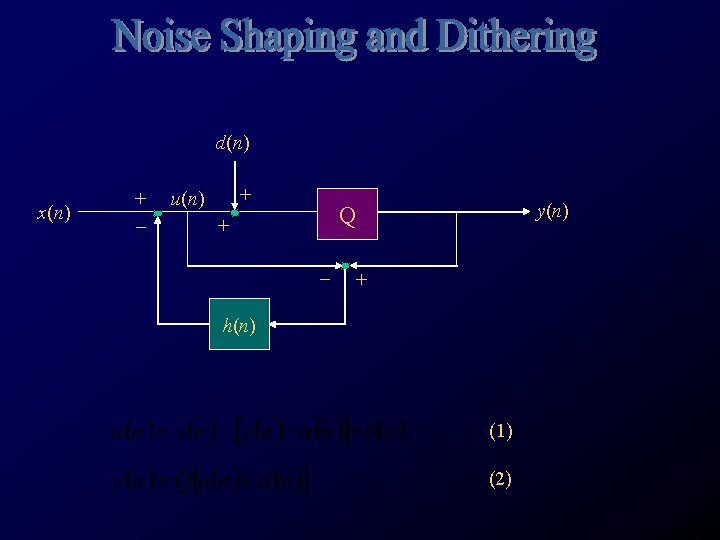
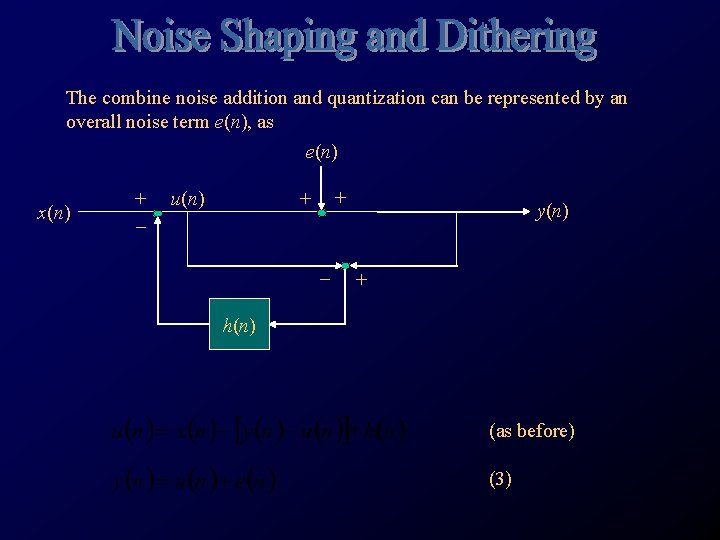
The combine noise addition and quantization can be represented by an overall noise term e(n), as e(n) x(n) + _ u(n) + + _ y(n) + h(n) (as before) (3)

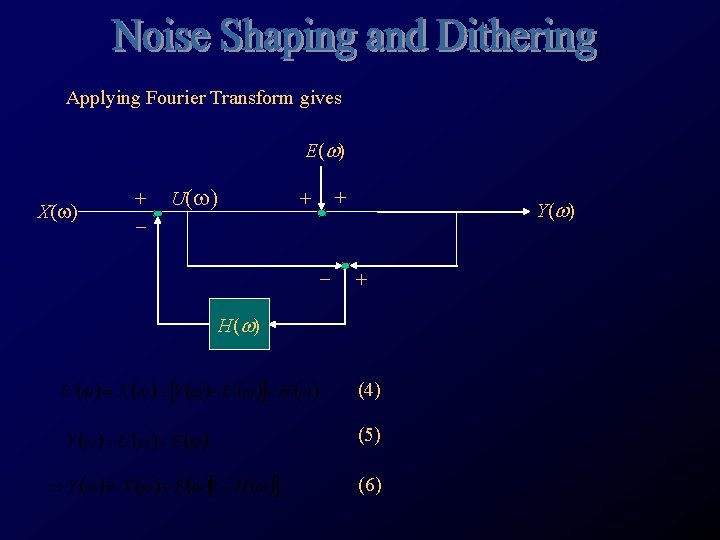
Applying Fourier Transform gives E(w) X(w) + _ U(w) + + _ Y(w) + H(w) (4) (5) (6)

(6) If H(w)=1 then the quantization error will be eliminated. However this kind of filter cannot be implemented in practice, alternatively different transfer function can be selected so that the noise will be attenuated more on the low frequency end. (7) (8) f w |N(w|2 db 0 0 0 -infinity fs/8 pi/4 0. 5 -3 fs/6 pi/3 1 0 fs/4 pi/2 2 3 fs/2 pi 4 6 Noted that the noise is attenuated more at the low frequency end than the higher end.

Noise power gain (9) Hence the noise shaper had increased the noise power by 3 d. B

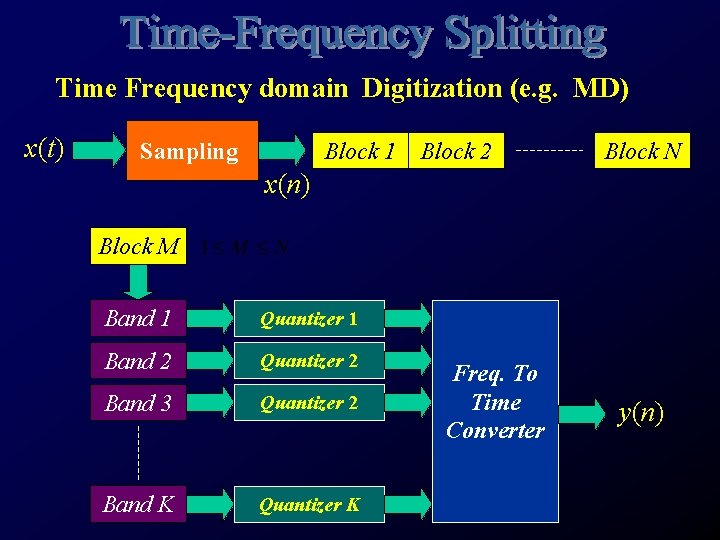
Time Frequency domain Digitization (e. g. MD) x(t) Sampling Block 1 Block 2 Block N x(n) Block M Band 1 Quantizer 1 Band 2 Quantizer 2 Band 3 Quantizer 2 Band K Quantizer K Freq. To Time Converter y(n)

1. Time signal is chopped into segments or blocks 2. Each block is transformed into its frequency spectrum 3. Frequency spectrum is partitioned into bands 4. Each band is digitized and quantized

5. In the player, each digitized band is converted back to analogue form 6. The frequency bands integrates to reconstruct the frequency spectrum 7. The frequency spectrum is transformed back to the time domain to reproduce the time segment. If each frequency band is quantized with the same number of levels, no compression is achieved. The extra, complicated effort is wasted

Compression is attained if certain bands can be quantized with less number of levels However, those bands will subject to more distortion The distortion is in the form of “Quantization Noise” Any solution to make both ends meet ?

Key researchers in the study of HAS 1. G. von Bekesy 2. J. B. Allen Noise is less audible at some Quantization frequencies than at others 3. H. Fletcher 4. B. Scharf 5. D. D. Greenwood Important Findings: Hearing Sensitivity, Tone-Masking -Noise, Critical Bands

“The brain interprets signal received via the auditory system rather than its objective representation. ” R Listeners grouped tones by frequency proximity, rather than the actual representation L R L Author: Diana Deutsch Source: http: //psy. ucsd. edu/~ddeutsch/psychology/figures/fig 3. jpg Copyright: Diana Deutsch

“When two identical but delayed audio sources are heard, the first one will inhibit the other if the delay is within 25 to 35 ms. ” This is true even if the second sound is 10 db above the first one. The result is sound seems to originate from the first source only, and the loudness is increased.

Frequency response of human ears is non-uniform The ear operates like a spectrum analyser Analyses with frequency (critical) bands 100 Hz below 500 Hz 1/6 to 1/3 of an octave above 500 Hz High energy in one band may inhibit neighboring bands Masking occurs after the masking tone starts and ends: Forward and backward masking

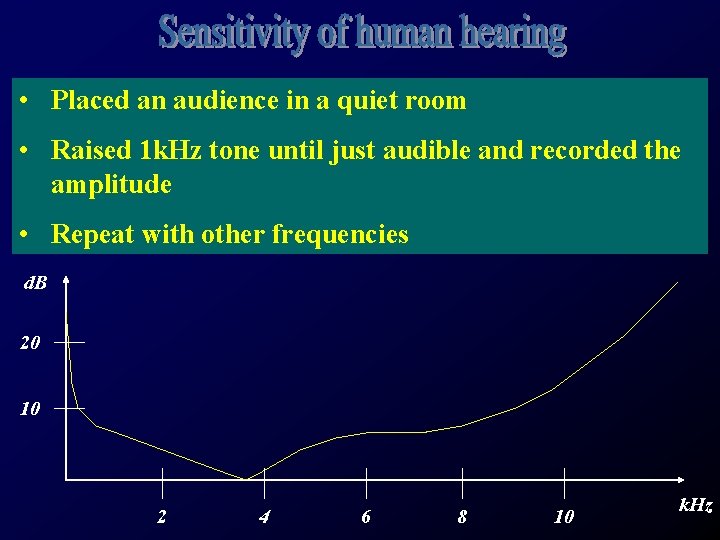
• Placed an audience in a quiet room • Raised 1 k. Hz tone until just audible and recorded the amplitude • Repeat with other frequencies d. B 20 10 2 4 6 8 10 k. Hz

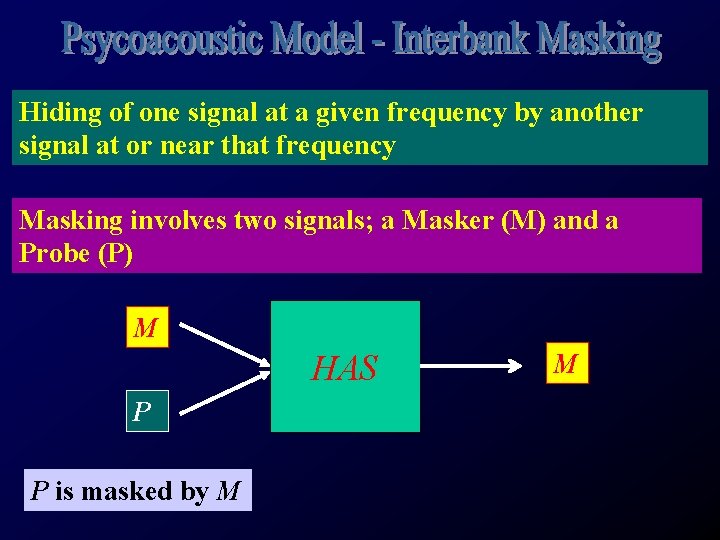
Hiding of one signal at a given frequency by another signal at or near that frequency Masking involves two signals; a Masker (M) and a Probe (P) M HAS P P is masked by M M

Hiding of one signal at a given frequency by another signal at or near that frequency Masking involves two signals; a Masker (M) and a Probe (P) M HAS M P The level when P is just audible is known as “just noticable difference (JND)

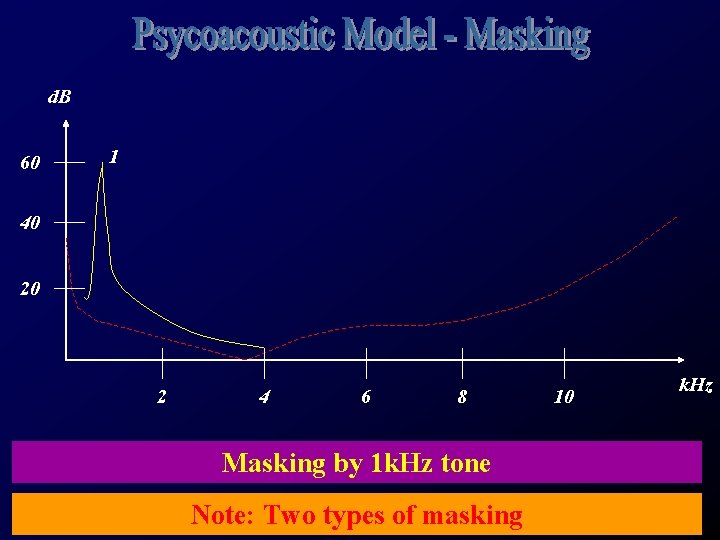
d. B 60 1 40 20 2 4 6 8 Masking by 1 k. Hz tone Note: Two types of masking 10 k. Hz

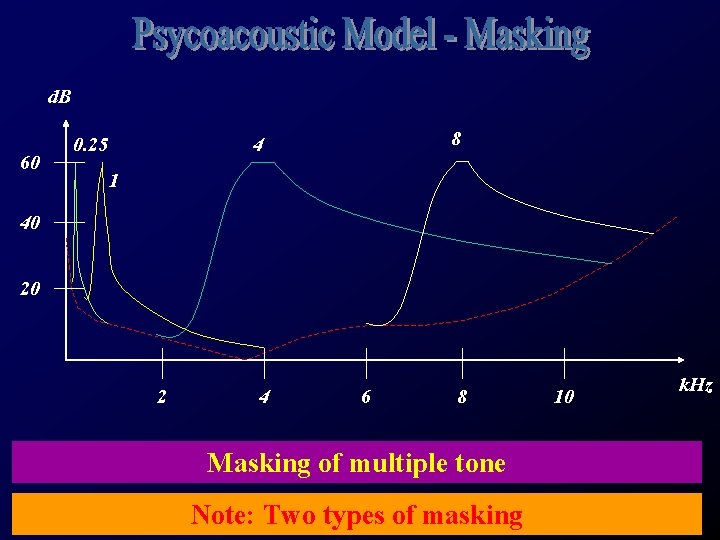
d. B 60 0. 25 8 4 1 40 20 2 4 6 8 Masking of multiple tone Note: Two types of masking 10 k. Hz

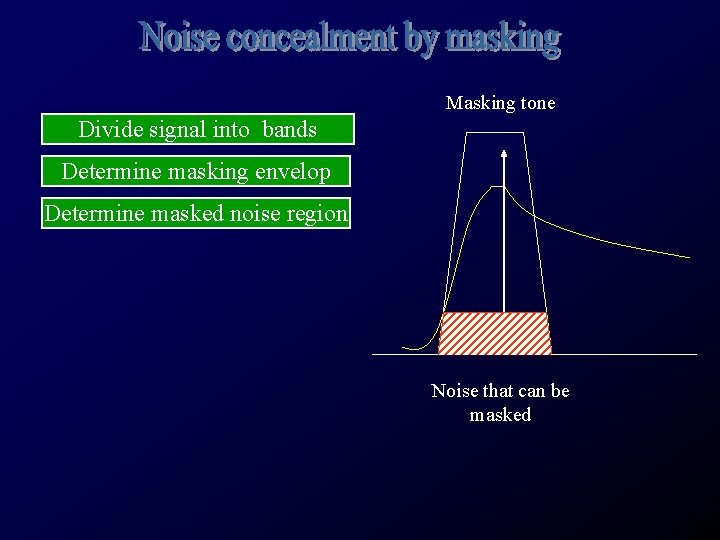
Masking tone Divide signal into bands Determine masking envelop Determine masked noise region Noise that can be masked

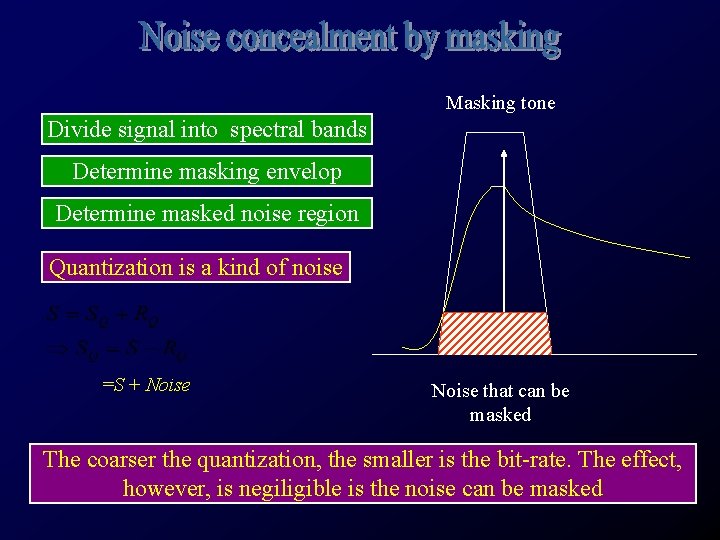
Masking tone Divide signal into spectral bands Determine masking envelop Determine masked noise region Quantization is a kind of noise =S + Noise that can be masked The coarser the quantization, the smaller is the bit-rate. The effect, however, is negiligible is the noise can be masked

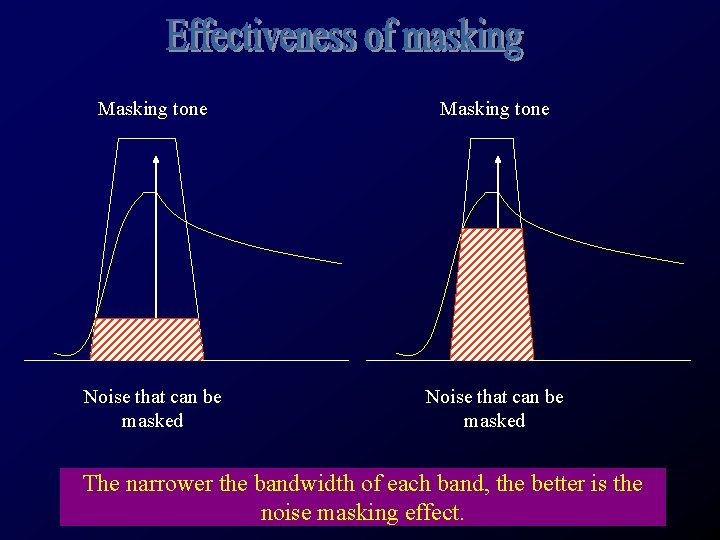
Masking tone Noise that can be masked The narrower the bandwidth of each band, the better is the noise masking effect.

Frequency resolution is best at low frequencies: Easier to discriminate different frequencies Time resolution is best at higher frequencies: Easier to locate the instance of a particular tone

Frequency resolution is best at low frequencies: Easier to discriminate different frequencies Time resolution is best at higher frequencies: Easier to locate the instance of a particular tone Suggest non-uniform partitioning of audio frequency spectrum

Partitioning of frequency spectrum into Critical Bands according to the Psychoacoustic model Standard: The Bark Scale (after Barkhausen) f

1 Bark

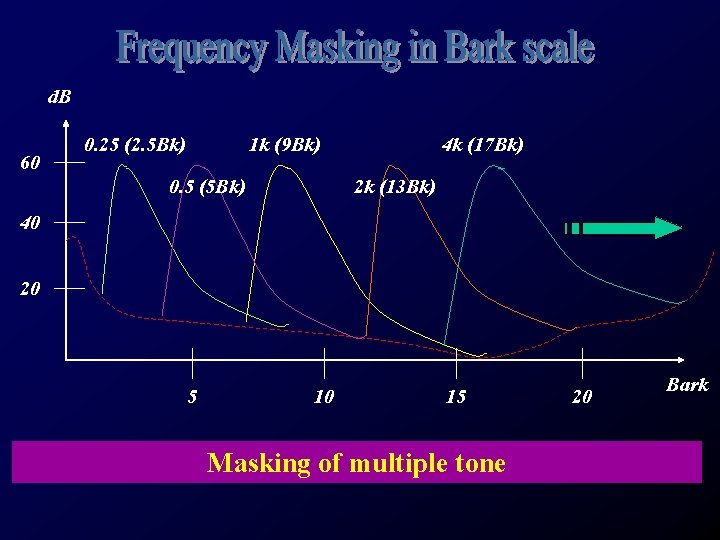
d. B 60 0. 25 (2. 5 Bk) 1 k (9 Bk) 0. 5 (5 Bk) 4 k (17 Bk) 2 k (13 Bk) 40 20 5 10 15 Masking of multiple tone 20 Bark

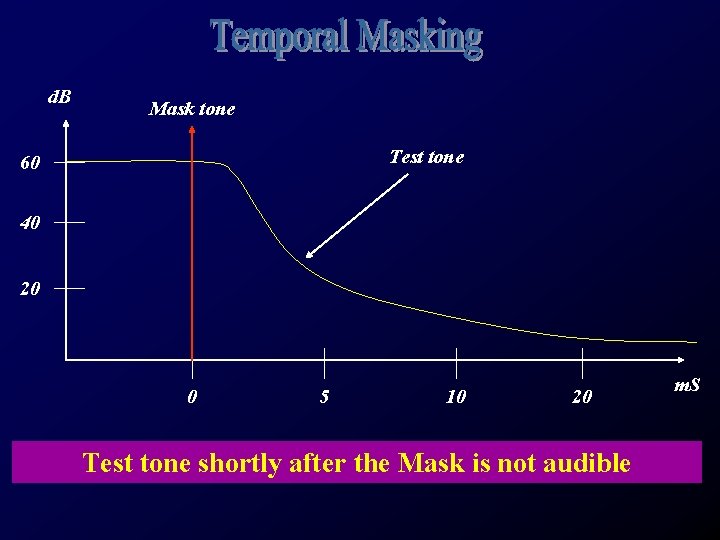
d. B Mask tone Test tone 60 40 20 0 5 10 20 Test tone shortly after the Mask is not audible m. S

Sensitivity of the ear varies with different frequency Most sensitive: around 4 k. Hz Less sensitive: at higher frequencies Quantization Noise is less audible at some frequencies than at others Simultaneous masking: A softer sound is less audible in the presence of a louder sound Quantization Noise is less audible at frequencies on, or closed to loud tones.

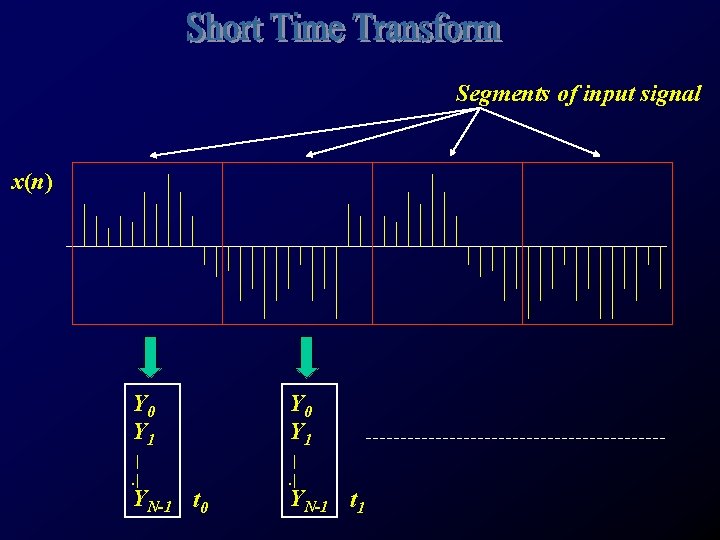
Segments of input signal x(n) Y 0 Y 1 |. | YN-1 t 0 YN-1 t 1

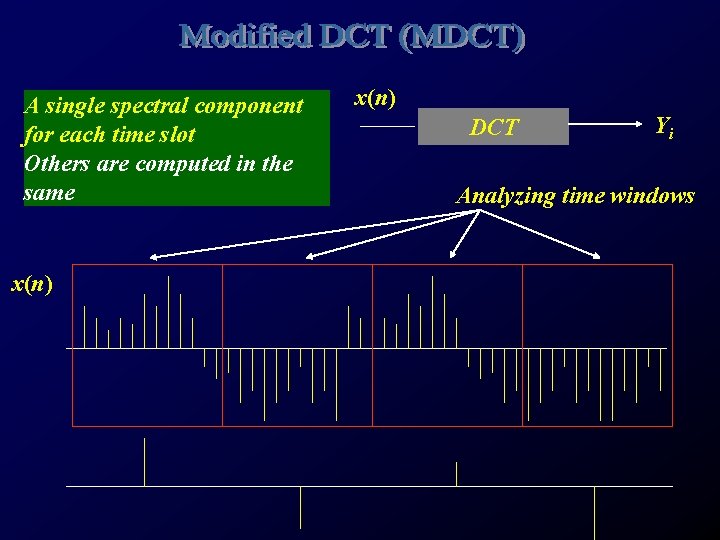
A single spectral component for each time slot Others are computed in the same x(n) DCT Yi Analyzing time windows

The MDCT blends one frame into the next to avoid inter-frame block boundary artifacts. The MDCT output of one frame is windowed according to MDCT requirements, overlapped 50% with the output of the previous frame and added. Case 1: equal sized-windows

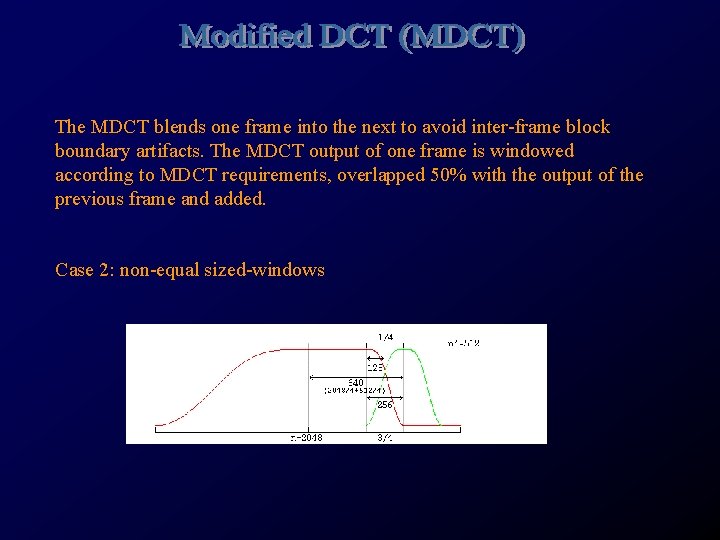
The MDCT blends one frame into the next to avoid inter-frame block boundary artifacts. The MDCT output of one frame is windowed according to MDCT requirements, overlapped 50% with the output of the previous frame and added. Case 2: non-equal sized-windows

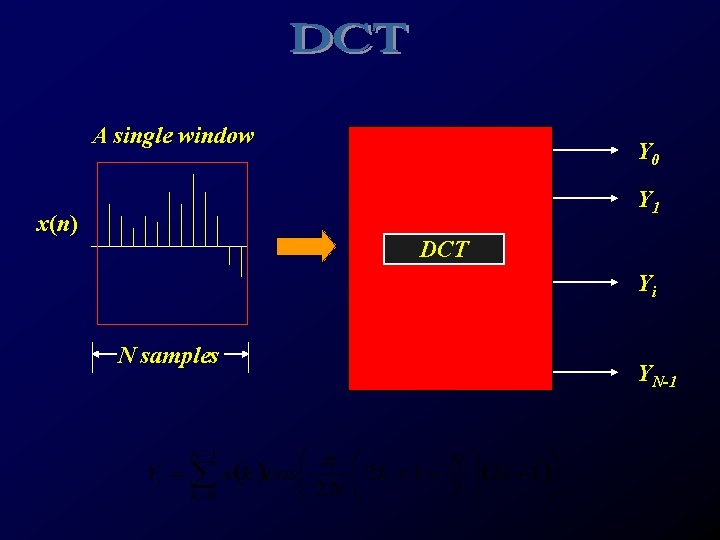
A single window Y 0 Y 1 x(n) DCT Yi N samples YN-1

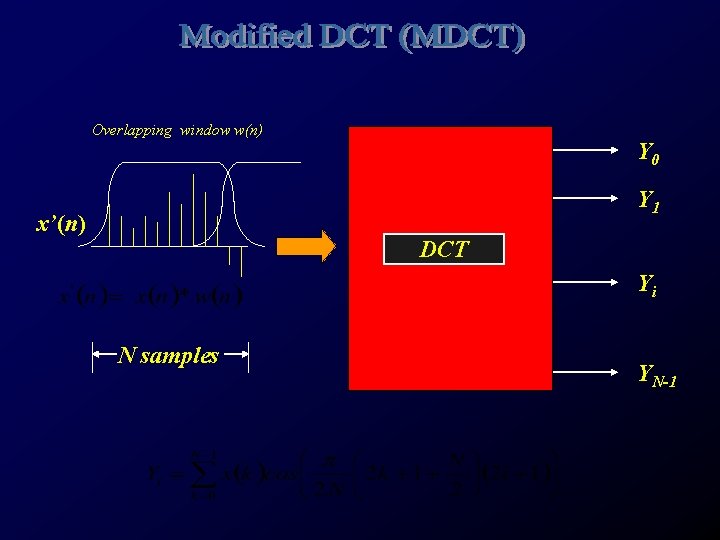
Overlapping window w(n) Y 0 Y 1 x’(n) DCT Yi N samples YN-1

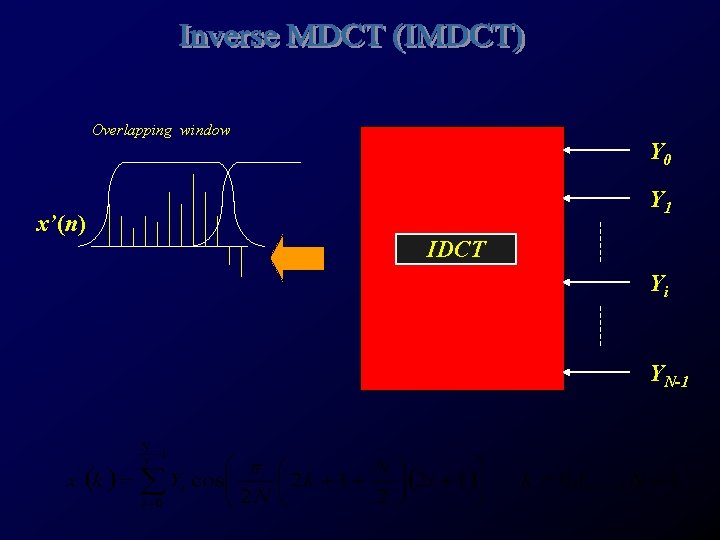
Overlapping window x’(n) Y 0 Y 1 IDCT Yi YN-1

Discard frequency band that is less essential to HAS Number of data samples x(n)= [x(0), x(1), . . . , x(N-1)] Decompose x(n) into N N N MDCT coefficients Select the coefficients that are sensitive to the HAS and discard the rest K<N (e. g. select K bands where K<N) Disadvantage: Noticable distortion on discarded bands

A better approach: Assign different quantization step-size to each coefficients according to their tolerance to quantization noise based on HAS x(n)= [x(0), x(1), . . . , x(N-1)] Decompose x(n) into N MDCT coefficients Quantize each coefficient so that the noise is below the masking threshold (1 bit = 6 d. B) Number of data samples N N

Source bit-rate: 1. 4 Mb/s Target bit-rate: 292 Kb/s A total of 52 critical bands 20 bands for lower frequencies 16 bands for middle frequencies 16 bands for higher frequencies Number of time windows: 8 Smallest time window: 1. 45 m. S Longest time window: 11. 60 m. S

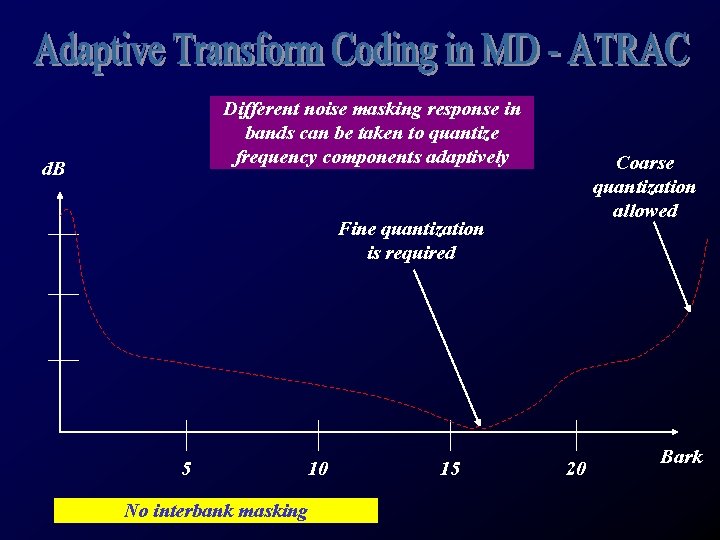
Different noise masking response in bands can be taken to quantize frequency components adaptively d. B Coarse quantization allowed Fine quantization is required 5 10 No interbank masking 15 20 Bark

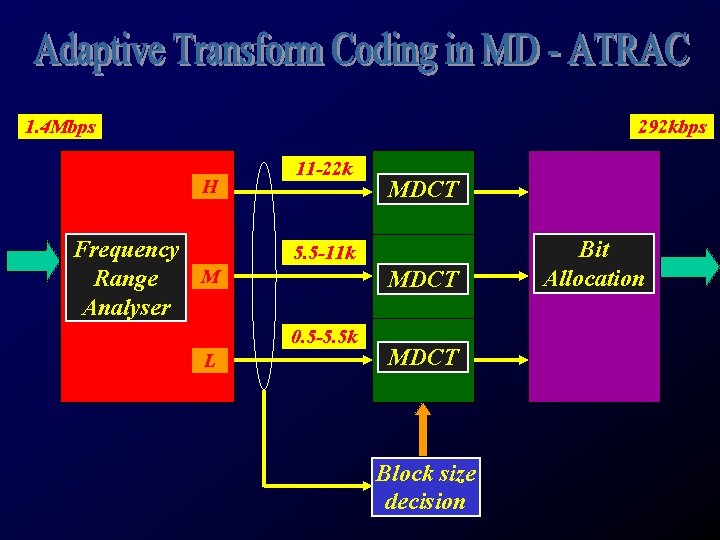
1. 4 Mbps 292 kbps H Frequency M Range Analyser 11 -22 k 5. 5 -11 k MDCT 0. 5 -5. 5 k L MDCT Block size decision Bit Allocation