Properties of Geometrical Figures Constructing Geometrical Figures using

Properties of Geometrical Figures Constructing Geometrical Figures using Geo. Gebra Created by Jade Wright, Prue Tinsey, Tania Young, Garth Lo Bello and Andrew Roberts

Mathematics • Stage 4 Measurement and Geometry Properties of Geometrical Figures 1 Outcomes A student: • Communicates and connects mathematical ideas using appropriate terminology, diagrams and symbols MA 4 -1 WM • Applies appropriate mathematical techniques to solve problems MA 4 -2 WM • Recognises and explains mathematical relationships using reasoning MA 4 -3 WM • Identifies and uses angle relationships, including those related to transversals on sets of parallel lines MA 4 -18 MG

Students: Classify triangles according to their side and angle properties and describe quadrilaterals (ACMMG 165) � Investigate the properties of special quadrilaterals (trapeziums, kites, parallelograms, rectangles, squares and rhombuses). Properties to be investigated include: ― The opposite sides are parallel ― The opposite sides are equal ― The adjacent sides are perpendicular ― The opposite angles are equal ― The diagonals bisect each other at right angles ― The diagonals bisect the angles of the quadrilateral Ø Use techniques such as paper folding, measurement or dynamic geometry software to investigate the properties of quadrilaterals (Problem Solving, Reasoning) Ø Sketch and label quadrilaterals from a worded or verbal description (Communicating) � Classify special quadrilaterals on the basis of their properties � Describe a quadrilateral in sufficient detail for it to be sketched

Student Activity In pairs students will use Geo. Gebra to construct a variety of geometrical figures to explore and investigate their properties

Geometrical Figures The geometrical figures we are going to investigate are: • Rectangle • Square • Triangle – Equilateral, Isosceles • Parallelogram • Rhombus

(1) (2) (3) (4) (5) (6) (7) (8) Let’s Look at the Properties of a Rectangle Opposite sides are parallel Opposite angles are equal Opposite sides are equal in length Diagonals bisect each other All four angles are right angles Adjacent sides are perpendicular Diagonals are equal in length Diagonals do not bisect each other at right angles

Now let’s construct a rectangle in Geo. Gebra To open Geo. Gebra: • Go to: www. geogebra. org • Click Download • Click Applet Start Now use the tools in Geo. Gebra to construct a rectangle Is your rectangle a construction or just a drawing? Use the drag test to determine if it is a construction

Here’s how to construct a Rectangle 1. Create segment AB. 2. Create a perpendicular line to segment AB through point B. 3. Insert a new point C on the perpendicular line. 4. Construct a parallel line to segment AB through point C. 5. Create a perpendicular line to segment AB through point A. 6. Construct intersection point D. 7. Create the polygon ABCD. 8. Hide the lines outside the rectangle. 9. Apply the drag test to check if the construction is correct.

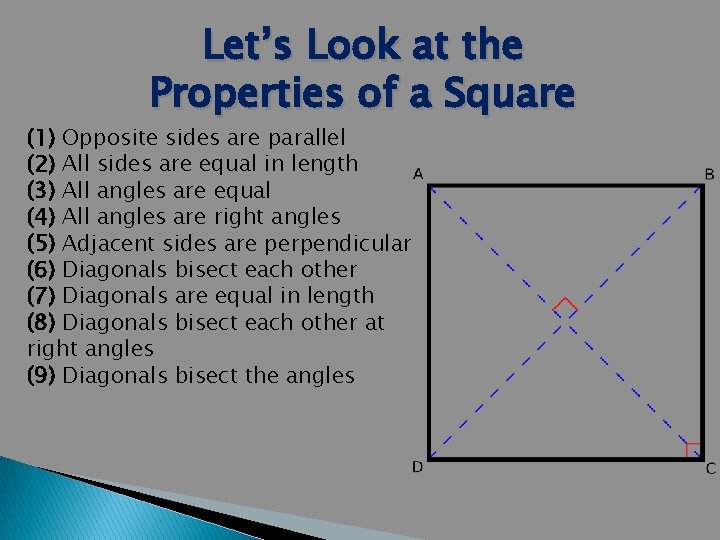
Let’s Look at the Properties of a Square (1) Opposite sides are parallel (2) All sides are equal in length (3) All angles are equal (4) All angles are right angles (5) Adjacent sides are perpendicular (6) Diagonals bisect each other (7) Diagonals are equal in length (8) Diagonals bisect each other at right angles (9) Diagonals bisect the angles

Now let’s construct a Square in Geo. Gebra Now use the tools in Geo. Gebra to construct a square Is your rectangle a construction or just a drawing? Use the drag test to determine if it is a construction

Here’s how to construct a Square 1. Create segment AB. 2. Create a perpendicular line to segment AB through point A. 3. Construct a circle with centre A through B. 4. Construct intersection point C. 5. Construct a parallel line to segment AB through point C. 6. Create a perpendicular line to segment AB through point B. 7. Construct intersection point D. 8. Create the polygon ABCD. 9. Apply the drag test to check if the construction is correct.

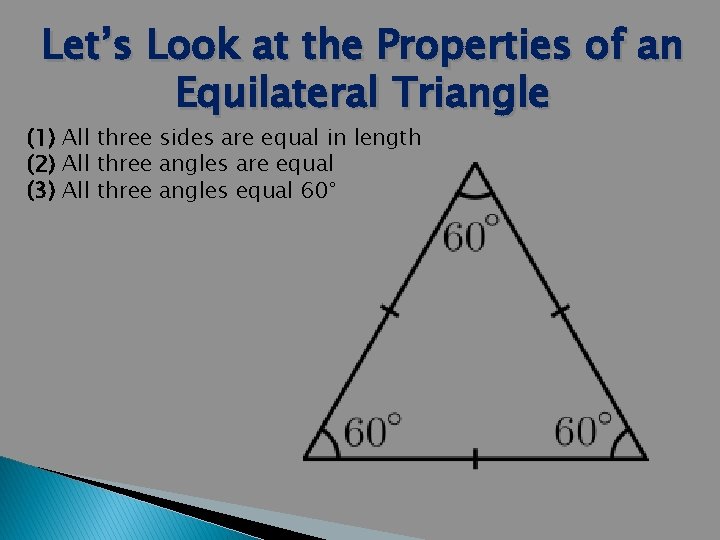
Let’s Look at the Properties of an Equilateral Triangle (1) All three sides are equal in length (2) All three angles are equal (3) All three angles equal 60°

Now let’s construct an Equilateral Triangle in Geo. Gebra Now use the tools in Geo. Gebra to construct an equilateral triangle Is your rectangle a construction or just a drawing? Use the drag test to determine if it is a construction

1. 2. 3. 4. 5. 6. 7. 8. Here’s how to construct an Equilateral Triangle Create segment AB. Construct a circle with centre A through B. Construct a circle with centre B through A. Intersect both circles to get point C. Create the polygon ABC in counter-clockwise direction. Hide the two circles. Show the interior angles of the triangle. Apply the drag test to check if the construction is correct.

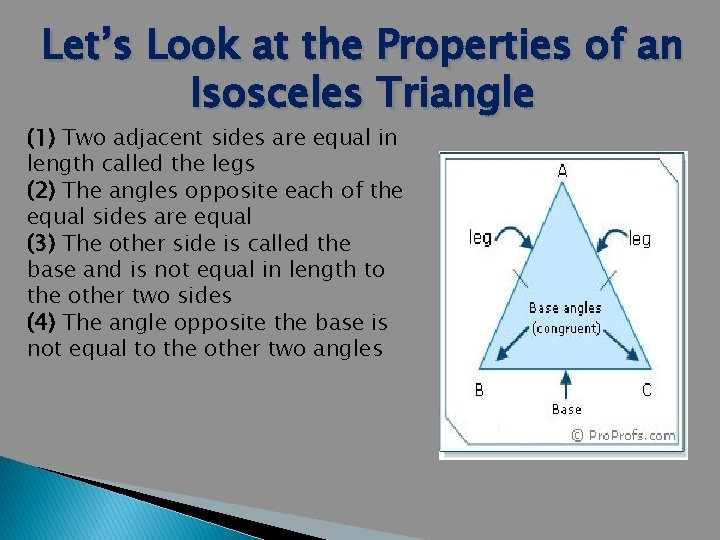
Let’s Look at the Properties of an Isosceles Triangle (1) Two adjacent sides are equal in length called the legs (2) The angles opposite each of the equal sides are equal (3) The other side is called the base and is not equal in length to the other two sides (4) The angle opposite the base is not equal to the other two angles

Now let’s construct an Isosceles Triangle in Geo. Gebra Now use the tools in Geo. Gebra to construct an isosceles triangle Is your rectangle a construction or just a drawing? Use the drag test to determine if it is a construction

1. 2. 3. 4. 5. 6. 7. 8. Here’s how to construct an Isosceles Triangle Create segment AB. Find midpoint of AB to create point C. Construct a perpendicular line through point C. Create new point D on perpendicular line. Create the polygon ABD in counter-clockwise direction. Hide any lines outside the triangle Show the interior angles of the triangle. Apply the drag test to check if the construction is correct.

(1) (2) (3) (4) (5) (6) Let’s Look at the Properties of a Parallelogram Opposite sides are parallel Opposite angles are equal Opposite sides are equal in length Diagonals bisect each other Diagonals do not bisect each other at right angles All angles are not right angles

Now let’s construct a Parallelogram in Geo. Gebra Now use the tools in Geo. Gebra to construct a parallelogram Is your rectangle a construction or just a drawing? Use the drag test to determine if it is a construction

1. 2. 3. 4. 5. 6. 7. 8. 9. Here’s how to construct a Parallelogram Create segment AB. Create new point C not on segment AB. Create line parallel to segment AB through point C. Create line BC. Create line parallel to segment BC through point A. Intersect two lines to create new point D. Create polygon ABCD. Hide any lines outside the parallelogram. Apply the drag test to check if the construction is correct.

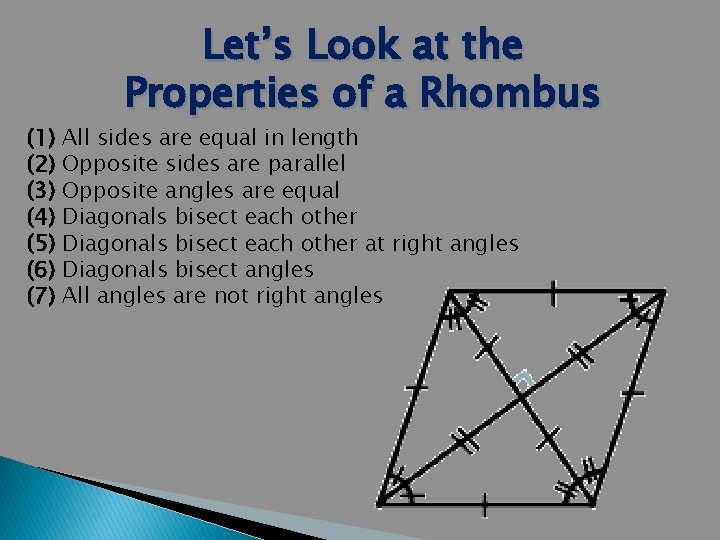
(1) (2) (3) (4) (5) (6) (7) Let’s Look at the Properties of a Rhombus All sides are equal in length Opposite sides are parallel Opposite angles are equal Diagonals bisect each other at right angles Diagonals bisect angles All angles are not right angles

Now let’s construct a Rhombus in Geo. Gebra Now use the tools in Geo. Gebra to construct a rhombus Is your rectangle a construction or just a drawing? Use the drag test to determine if it is a construction

Here’s how to construct a Rhombus 1. Create segment AB. 2. Construct a circle with centre A through B. 3. Construct a circle with centre B through A. 4. Intersect two circles to create new point C. 5. Create line parallel to segment AB through point C. 6. Create line AC. 7. Create line parallel to segment AC through point B. 8. Intersect two lines to create new point E. 9. Create polygon ABEC. 10. Hide any lines outside the rhombus. 11. Apply the drag test to check if the construction is correct.

Student Activity Now let’s test your knowledge 1. 2. 3. 4. 5. In pairs students will work together to test each others knowledge. One student will pick a geometrical figure (without telling their partner) and read its properties to the other student. This student will then construct the figure in Geo. Gebra based on the description given by their partner. The student reading the properties will then check whether their partner has constructed the correct figure and use the drag test to test whether it is a “real” construction. Now you will take it in turns until you’ve each constructed each shape.

Student Activity Real World Application Geometry is used everywhere. Architecture is one example of how geometry is used in the real world. This task requires you to investigate the architecture used to design the Eiffel tower The Task In groups of 2 examine the geometry that can be found in architecture used to build the Eiffel tower. You will need to: 1. Label the geometric shapes in the Eiffel tower, using images found from internet resources. You can investigate these shapes in Geo. Gebra to verify their properties. 2. Create a Power. Point presentation to report these findings. Concepts that you should cover, include: - a brief history on the time and place of construction - why it was constructed - a description of your geometric findings, regarding the architecture of the building. For example, the shapes used to create the building, and an explanation why this geometry is so important in the building of the Eiffel tower.

Thankyou for listening Any Questions?