Properties of Functions Objectives Determine and Identify Even

Properties of Functions Objectives: Determine and Identify Even and Odd Functions from a Graph or from the Equation Use a graph to determine where a Function is Increasing, Decreasing or Constant Use a graph to locate Local Maxima and Minima Find the Average Rate of Change of a Function

Properties of Functions � It is easiest to obtain the graph of a function by knowing certain properties that the function has and the impact of these properties on the way that the graph will look. In this section we describe some properties of functions that we will use in subsequent chapters. ◦ ◦ ◦ Zeros of f Symmetry Increasing, Decreasing or Constant Local Maximum or Minimum Average Rate of Change

Properties of Functions � � � Intercepts: If is in the domain of a function , then the y-intercept of the graph of is the value of , which is. The x-intercepts of the graph of , if there any, are the solutions of the equation Symmetry: A function is even if and only if, whenever the point is on the graph of , then the point is also on the graph. (symmetric with respect to the y-axis) A function is odd if and only if, whenever the point is on the graph of , then the point is also on the graph. (symmetric with respect to the origin)

Properties of Functions � � � A function choice of is increasing on an open interval , with , we have if, for any A function choice of is decreasing on an open interval , with , we have if, for any A function is constant on an interval , the values are equal. if, for all choices of A function has a local maximum at c, if there is an open interval containing c so that, for all. We call a local maximum of f. A function has a local minimum at c, if there is an open interval containing c so that, for all. We call a local minimum of f.
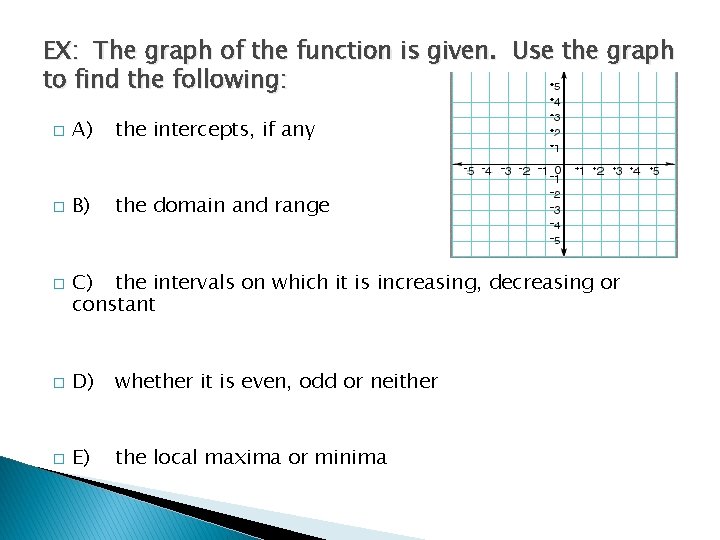
EX: The graph of the function is given. Use the graph to find the following: � A) the intercepts, if any � B) the domain and range � C) the intervals on which it is increasing, decreasing or constant � D) whether it is even, odd or neither � E) the local maxima or minima
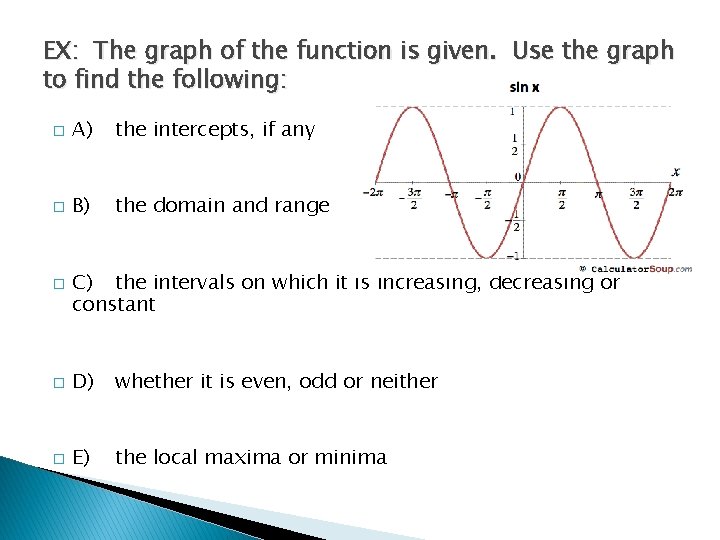
EX: The graph of the function is given. Use the graph to find the following: � A) the intercepts, if any � B) the domain and range � C) the intervals on which it is increasing, decreasing or constant � D) whether it is even, odd or neither � E) the local maxima or minima

Average Rate of Change � � � If is in the domain of a function of change of from is defined as , the average rate (To find the average rate of change of a function between any two points on its graph, we calculate the slope of the line containing the two points) In Calculus, this expression is called the difference quotient

EX: Find the average rate of change of a function � 1. ◦ A) From 1 to 3 ◦ B) From 2 to 5 ◦ C) From 3 to 7

Ex: Determine algebraically whether each function is even, odd or neither � 1. 2.
- Slides: 9