Properties of Equality and Solving OneStep Equations Vocabulary

Properties of Equality and Solving One-Step Equations

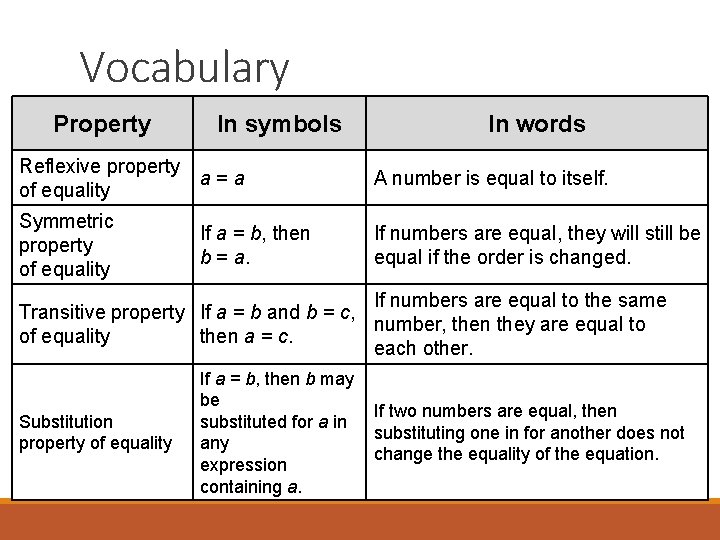
Vocabulary Property In symbols In words Reflexive property a = a of equality A number is equal to itself. Symmetric property of equality If numbers are equal, they will still be equal if the order is changed. If a = b, then b = a. If numbers are equal to the same Transitive property If a = b and b = c, number, then they are equal to of equality then a = c. each other. Substitution property of equality If a = b, then b may be If two numbers are equal, then substituted for a in substituting one in for another does not any change the equality of the equation. expression containing a.

Property Addition property of equality In symbols In words If a = b, then a + c = b + c. Adding the same number to both sides of an equation does not change the equality of the equation. Subtraction If a = b, then property of equality a – c = b – c. Subtracting the same number from both sides of an equation does not change the equality of the equation. If a = b and Multiplication c ≠ 0, then property of equality a • c = b • c. Multiplying both sides of the equation by the same number, other than 0, does not change the equality of the equation. Division property of equality If a = b and c ≠ 0, then a ÷ c = b ÷ c. Dividing both sides of the equation by the same number, other than 0, does not change the equality of the equation.

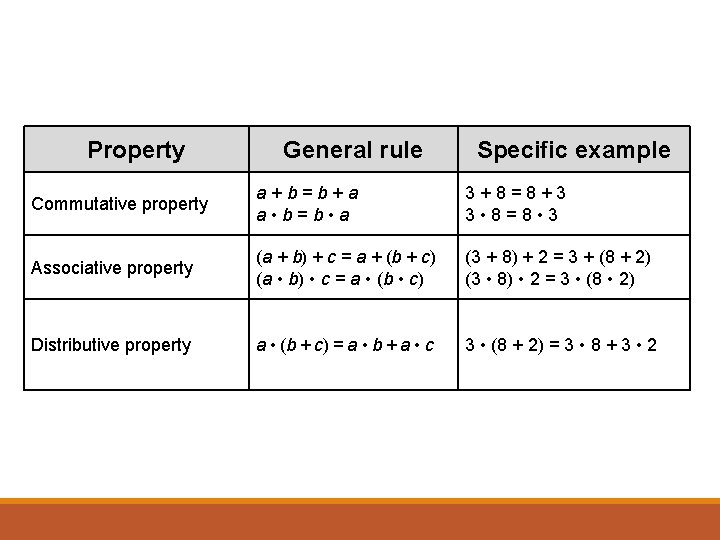
Property General rule Specific example Commutative property a + b = b + a a • b = b • a 3 + 8 = 8 + 3 3 • 8 = 8 • 3 Associative property (a + b) + c = a + (b + c) (a • b) • c = a • (b • c) (3 + 8) + 2 = 3 + (8 + 2) (3 • 8) • 2 = 3 • (8 • 2) Distributive property a • (b + c) = a • b + a • c 3 • (8 + 2) = 3 • 8 + 3 • 2

Like Terms

Combining Like Terms To combine like terms add the coefficients. coefficient 2 x variable

Example Given: 2 x - 4 y - 3 x + 7 y Combine like terms.

Example

SOLVING EQUATIONS Solving an equation for a variable means finding the values of the variable that make the equation true. To do this we must isolate the variable to one side of the equation by using inverse operations.

Inverse Operations Inverse operations undo operations; you can think of them as opposites. -Addition and subtraction are inverse operations. -Multiplication and division are inverse operations.

An equation is like a balance scale because it shows that two quantities are equal. What you do to one side of the equation must also be done to the other side to keep it balanced.

Example Given: k + 5 = 17 solve for k.

Example Given: 2 x = 18 solve for x.

Example Given: 9 + x = 20 solve for x.