Properties of Algebra There are various properties from

Properties of Algebra • There are various properties from algebra that allow us to perform certain tasks. • We review them now to refresh your memory on the process and terminology. • We will also add a few new properties which you might not be familiar.

“Indubitably. ” “The proof is in the pudding. ” Le pompt de pompt le solve de crime!" Deductive Reasoning Je solve le crime. Pompt de pompt. "

Properties of Equality Addition property of equality If a = b and c = d, then a + c = b + d. restated If a = b and c = d, then a + c = b + d. Example a=b 3=3 a+3=b+3 Euclid referred to this property as… “Equals when added to equals are equal. ”

Properties of Equality Subtraction property of equality If a = b and c = d, then a - c = b - d. restated If a = b and c = d, then a - c = b - d. Example a=b 3=3 a-3=b-3 Euclid referred to this property as… “Equals when subtracted from equals are equal. ”

Properties of Equality Multiplication property of equality If a = b and c = d, then ac = bd. restated If a = b and c = d, then ac = bd. Example a=b 3=3 3 a = 3 b Euclid referred to this property as… “Equals when multiplied by equals are equal. ”

Properties of Equality Division property of equality If a = b and , then restated If a = b and c = c, then Example a=b 3=3 Euclid referred to this property as… “Equals when divided by equals are equal. ”

Properties of Equality Division property of equality If a = b and , then restated If a = b and c = c, then Why must c not equal zero? You are not allowed to divide by zero. Numbers divided by zero are undefined. Euclid referred to this property as… “Equals when divided by equals are equal. ”

Properties of Equality Reflexive property of equality a=a This is really obvious. Nevertheless, it needs a name. When you look into a mirror, you see your reflection. Think of the equal sign as a mirror. It might help you remember the term.

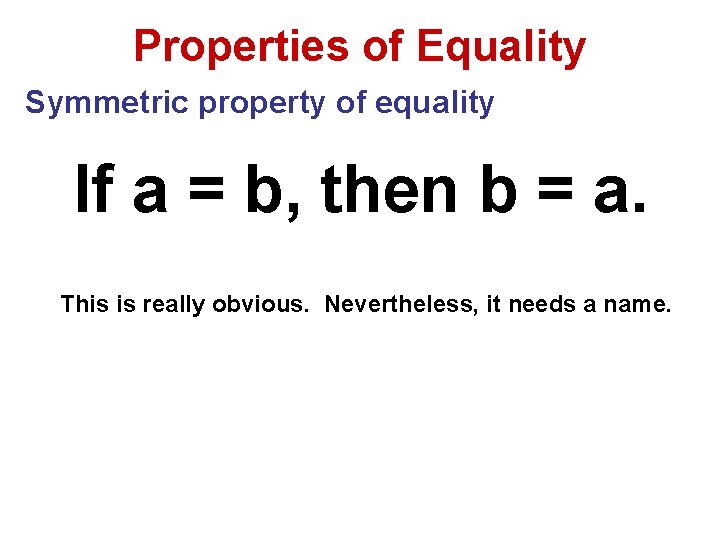
Properties of Equality Symmetric property of equality If a = b, then b = a. This is really obvious. Nevertheless, it needs a name.

Properties of Equality Transitive property of equality If a = b and b = c, then a = c. This is really obvious. Nevertheless, it needs a name. It might be helpful to associate this concept with traveling from LA to NYC with a stop over at Chicago. The transfer of planes allows you to reach your final destination.

Properties of Congruence Reflexive property of congruence This is really obvious. Nevertheless, it needs a name. When you look into a mirror, you see your reflection. Think of the equal sign as a mirror. It might help you remember the term. Didn’t we say this before? YES

Properties of Congruence Symmetric property of Congurence If If , then . This is really obvious. Nevertheless, it needs a name. Symmetric is the same for equality and congruence.

Properties of Congruence Transitive property of Congruence It might be helpful to associate this concept with traveling from LA to NYC with a stop over at Chicago. The transfer of planes allows you to reach your final destination. This is the same as in equality.

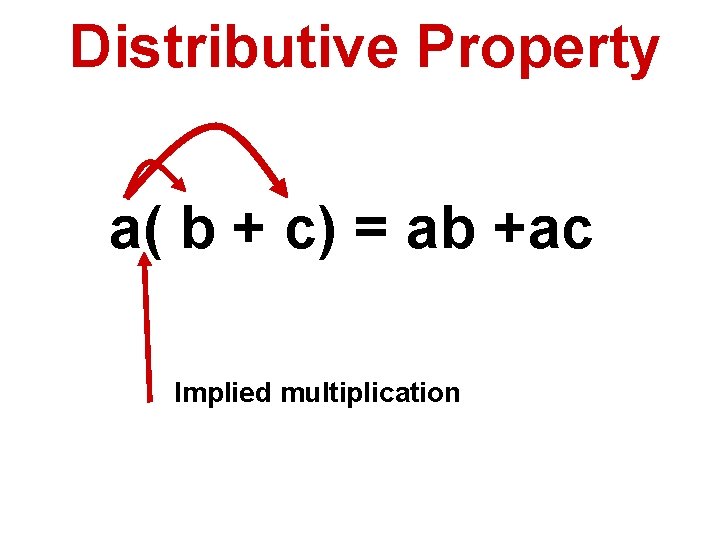
Distributive Property a( b + c) = ab +ac Implied multiplication

Recognition of Properties 1 If AB = CD , then Definition of congruent segments. If a = b and b = c, then a = c. Transitive property of equality. If a + b = 10 and b = 3, then a + 3 = 10. Substitution property of equality. If then AB = CD. Definition of congruent segments.

Recognition of Properties 2 If a = b and x = y , then a + x = b + y. +x +y Addition property of equality. If a = b and x = y , then a - x = b - y. -x -y Subtraction property of equality. If a = 7, then a + 3 = 10. +3 +3 Why? Addition property of equality. I added 3 to both sides. Remember Euclid? “Equals when added to equals are equal. ”

Recognition of Properties 3 If B is on line AC and AB = BC , then b is the midpoint of Definition of midpoint. If A = B , then A + 3 = B + 3. +3 +3 switch sides Addition property of equality. Symmetric property of equality. Reflexive property of equality. Mirror image

Recognition of Properties 4 11( 4 x + 7) = 44 x + 77 Distributive property. If a = b and b = c and c = 11, then a = 11. Transitive property of equality. If a = 11 , then a – 3 = 8. -3 -3 Subtraction property of equality. If a = b and c = 12, then c c Division property of equality.

Recognition of Properties 5 If 7 7 , then a = 42. Multiplication property of equality. If __ 8 x = 48, ___ then x = 6. Division property of equality. 8 8 If 2 y – 7 = 11, then 2 y = 18. +7 +7 If Addition property of equality. then switch sides Symmetric property of equality.

Recognition of Properties 6 If AB = 30 and A = 5 , then 5 B = 30. Substitution property of equality. If B is the midpoint of , then AB = BC. Definition of midpoint.

Proofs You have been doing proofs all along in Algebra I. When? When you solved equations, you were actually doing proofs – algebraic proofs. The major difference between equations and geometric proofs is in the form. 7( x + 2 ) = 35 7 x + 14 = 35 14 = 14 7 x = 21 7=7 x=3 Solving a first degree equation with 1 variable.

Proofs The major difference between equations and geometric proofs is in the form. If 7( x + 2 ) = 35, then x =3. Statements 7( x + 2 ) = 35 7 x + 14 = 35 14 = 14 7 x = 21 7=7 x=3 Written as a conditional. Reasons Given Information Distributive Property Reflexive Property Subtraction Prop. Of Equality Reflexive Property Division Prop. Of Equality The only difference is that the reasons/justification for each step must be written in geometry.

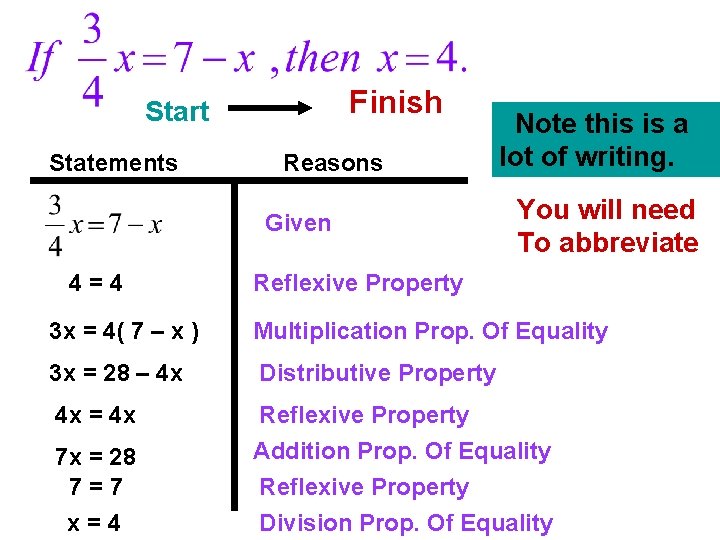
Finish Start Statements Reasons Given 4=4 Note this is a lot of writing. You will need To abbreviate Reflexive Property 3 x = 4( 7 – x ) Multiplication Prop. Of Equality 3 x = 28 – 4 x Distributive Property 4 x = 4 x Reflexive Property Addition Prop. Of Equality Reflexive Property Division Prop. Of Equality 7 x = 28 7=7 x=4

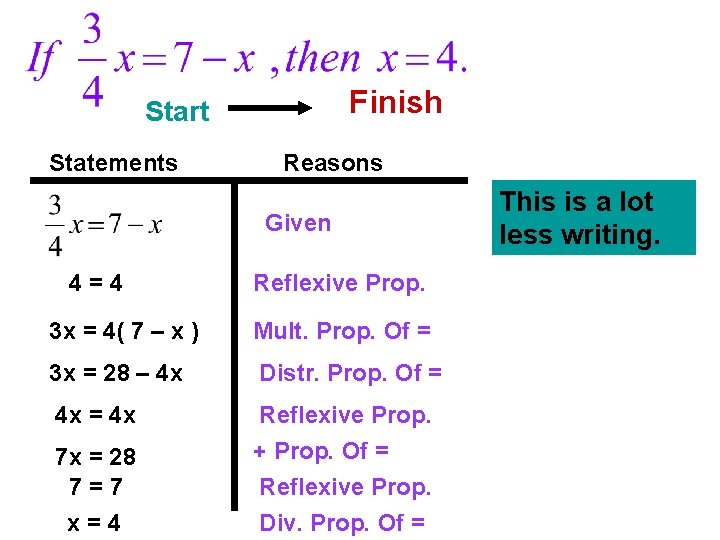
Finish Start Statements Reasons Given 4=4 Reflexive Prop. 3 x = 4( 7 – x ) Mult. Prop. Of = 3 x = 28 – 4 x Distr. Prop. Of = 4 x Reflexive Prop. + Prop. Of = Reflexive Prop. Div. Prop. Of = 7 x = 28 7=7 x=4 This is a lot less writing.

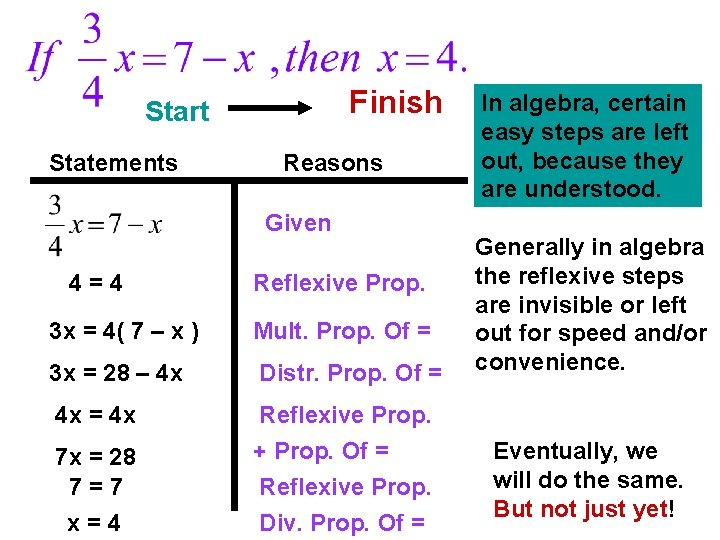
Finish Start Statements Reasons Given 4=4 Reflexive Prop. 3 x = 4( 7 – x ) Mult. Prop. Of = 3 x = 28 – 4 x Distr. Prop. Of = 4 x Reflexive Prop. + Prop. Of = Reflexive Prop. Div. Prop. Of = 7 x = 28 7=7 x=4 In algebra, certain easy steps are left out, because they are understood. Generally in algebra the reflexive steps are invisible or left out for speed and/or convenience. Eventually, we will do the same. But not just yet!

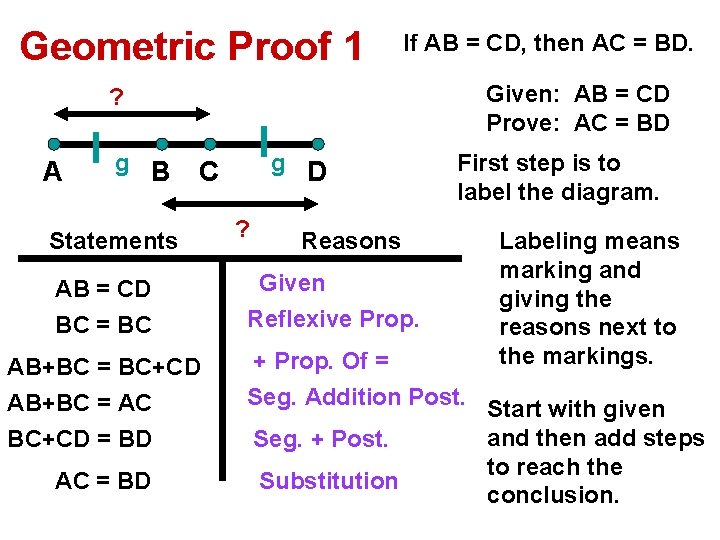
Geometric Proof 1 If AB = CD, then AC = BD. Given: AB = CD Prove: AC = BD ? A g B Statements AB = CD BC = BC AB+BC = BC+CD AB+BC = AC BC+CD = BD AC = BD g D C ? Reasons Given Reflexive Prop. First step is to label the diagram. Labeling means marking and giving the reasons next to the markings. + Prop. Of = Seg. Addition Post. Start with given and then add steps Seg. + Post. to reach the Substitution conclusion.

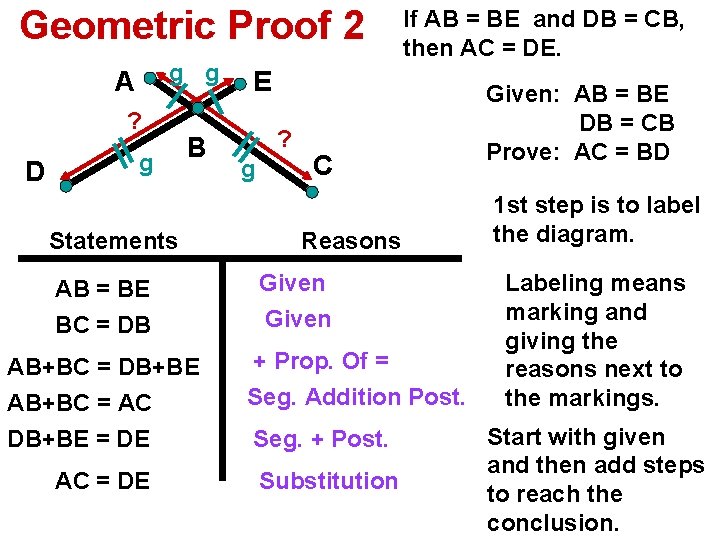
Geometric Proof 2 g g A ? D g B Statements AB = BE BC = DB AB+BC = DB+BE AB+BC = AC DB+BE = DE AC = DE If AB = BE and DB = CB, then AC = DE. E ? g C Reasons Given + Prop. Of = Seg. Addition Post. Seg. + Post. Substitution Given: AB = BE DB = CB Prove: AC = BD 1 st step is to label the diagram. Labeling means marking and giving the reasons next to the markings. Start with given and then add steps to reach the conclusion.

Summary 1 The properties of algebra are used as reasons or justifications of steps in proofs. 2 Four of the properties are associated with arithmetic operations in equations Euclid said it simply as: Added Equals when Subtracted by equals are equal. Multiplied Divided Addition Each one is known as the Subtraction property of equality. Multiplication Division

Summary 3 The distributive property involves parentheses. a( b + c ) = ab + ac Multiplication is distributed to each item inside the parentheses. 4 Proofs are a process of linking statement together from the hypotheses to the conclusion. It will take over a month to get comfortable with the process of writing proofs. Relax. Be patient. (hard to do) It WILL come.

C’est fini. Good day and good luck.