Proofs using Similar Triangles 1 of 7 Boardworks

Proofs using Similar Triangles 1 of 7 © Boardworks 2012

Information 2 of 7 © Boardworks 2012

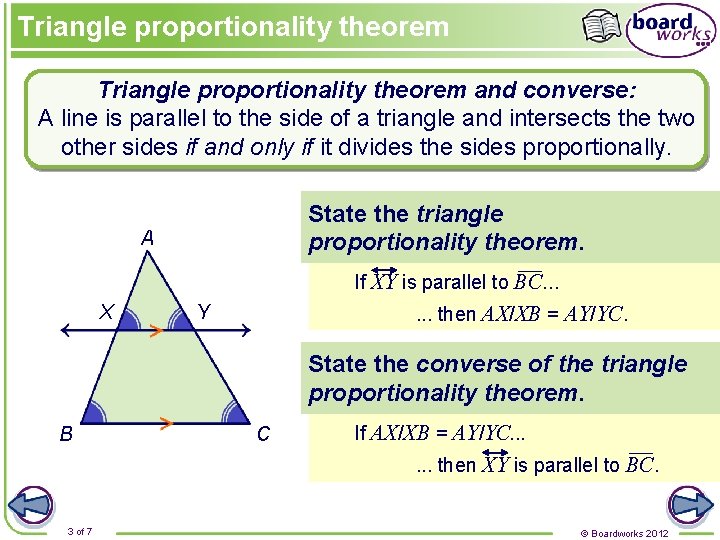
Triangle proportionality theorem and converse: A line is parallel to the side of a triangle and intersects the two other sides if and only if it divides the sides proportionally. State the triangle proportionality theorem. A If XY is parallel to BC. . . X Y . . . then AX/XB = AY/YC. State the converse of the triangle proportionality theorem. B C If AX/XB = AY/YC. . . then XY is parallel to BC. 3 of 7 © Boardworks 2012

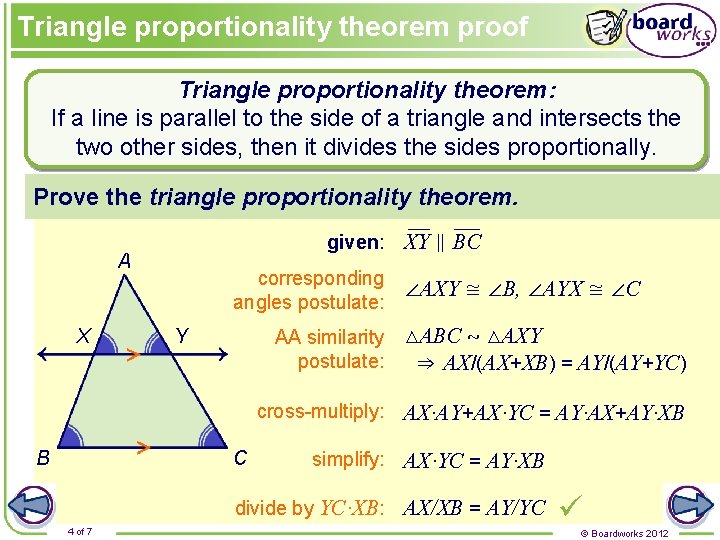
Triangle proportionality theorem proof Triangle proportionality theorem: If a line is parallel to the side of a triangle and intersects the two other sides, then it divides the sides proportionally. Prove the triangle proportionality theorem. given: XY ∥ BC A X corresponding ∠AXY ≅ ∠B, ∠AYX ≅ ∠C angles postulate: AA similarity △ABC ~ △AXY postulate: ⇒ AX/(AX+XB) = AY/(AY+YC) Y cross-multiply: AX·AY+AX·YC = AY·AX+AY·XB B C simplify: AX·YC = AY·XB divide by YC·XB: AX/XB = AY/YC 4 of 7 © Boardworks 2012

Converse of the triangle prop. theorem Converse of the triangle proportionality theorem: If a line divides two sides of a triangle proportionally, then it is parallel to the other side. Prove the converse of the triangle proportionality theorem. given: cross-multiply : A add AX·AY: X Y factor: substitute: rearrange: reflex. prop. : C SAS similarity postulate: B conv. corr. ang. theorem: 5 of 7 AX/XB = AY/YC AX·YC = AY·XB AX·YC+AX·AY = AY·XB+AX·AY AX(AY+YC) = AY(AX+XB) AX(AC) = AY(AB) AX/AB = AY/AC ∠A ≅ ∠ A △ABC ~ △AXY ⇒ ∠AXY ≅ ∠B, ∠AYX ≅ ∠C XY ∥ BC © Boardworks 2012

Similar triangles 6 of 7 © Boardworks 2012

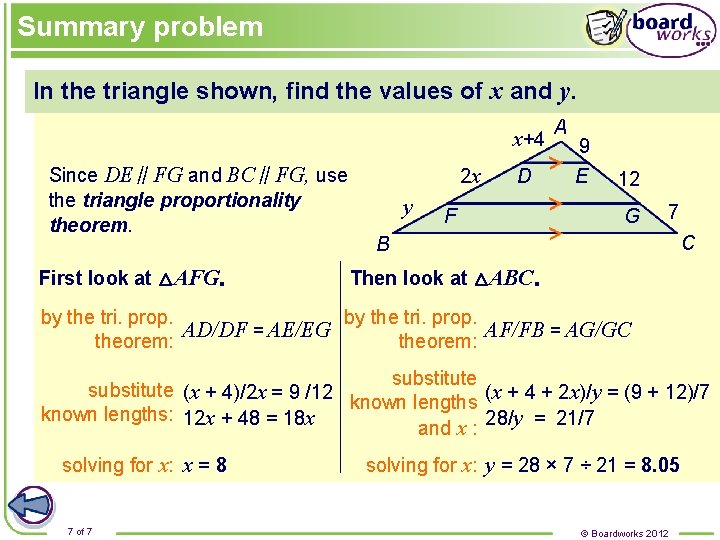
Summary problem In the triangle shown, find the values of x and y. x+4 Since DE∥FG and BC∥FG, use the triangle proportionality theorem. First look at △AFG. 2 x y D F A 9 E 12 G 7 C B Then look at △ABC. by the tri. prop. AD/DF = AE/EG AF/FB = AG/GC theorem: substitute (x + 4)/2 x = 9 /12 known lengths (x + 4 + 2 x)/y = (9 + 12)/7 known lengths: 12 x + 48 = 18 x and x : 28/y = 21/7 solving for x: x = 8 7 of 7 solving for x: y = 28 × 7 ÷ 21 = 8. 05 © Boardworks 2012