Proof Uniquely Mathematical and Creative Jim Hogan School

Proof… Uniquely Mathematical and Creative Jim Hogan, School Support Services Waikato University Inspiration from Dr. Paul Brown, Carmel School, WA Paul presented a similar workshop at MAV Conference, 2008. I enjoyed the session so much I decided then to present my version here in Palmerston North. Thanks also to a little book called Q. E. D. Beauty in Mathematical Proof written by Burkard Polster. See last slide for all contact details.

What will we learn today? • • Well, who knows? Proof is the pudding! There a few problems to ponder We might experience joy of proof You might find a useful resource Your students might benefit Aspects of the NZC may be made clear and we must do something with π

Proof It is nice to experience surprise! Like a good cryptic clue P 14. Clothes appear wrong when put on a number (7) L

Visual Proof What is the sum of n odd numbers? 1 st 2 nd 3 rd 4 th … nth 1 + 3 + 5 + 7 + … (2 n-1) = ?

Visual Proof What is the sum of n even numbers? 1 st 2 nd 3 rd 4 th … nth 2 + 4 + 6 + 8 + … 2 n = ? This presents a nice opportunity to show the square and a side; n 2 + n = n(n + 1)

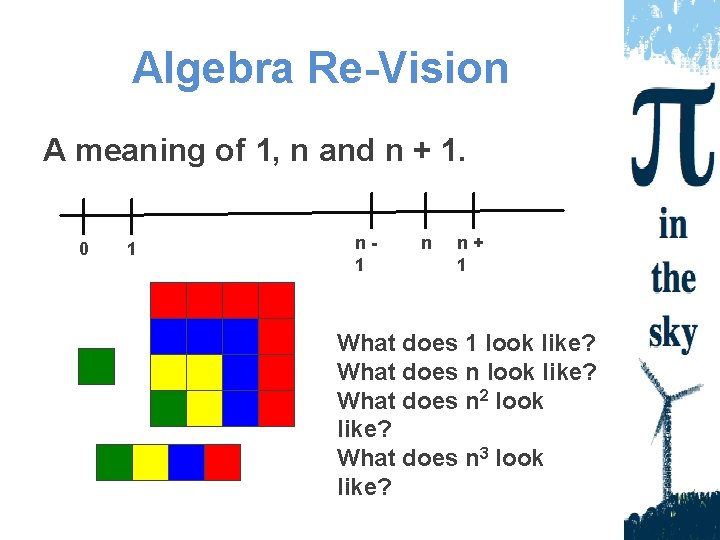
Algebra Re-Vision A meaning of 1, n and n + 1. 0 1 n n+ 1 What does 1 look like? What does n 2 look like? What does n 3 look like?

Visual Proof What is the sum of n counting numbers? 2 + 4 + 6 + 8 + … 2 n = n 2 + n 1 + 2 + 3 + 4 +… n = ? Notice that halving the even numbers makes the counting numbers. How does that help?

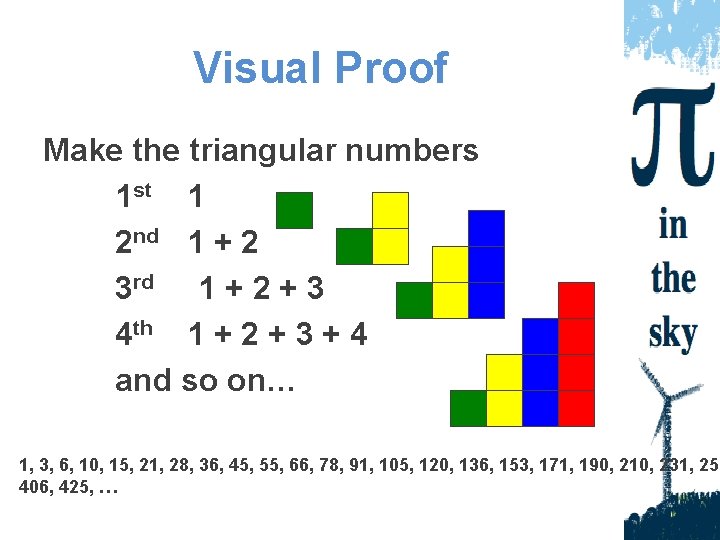
Visual Proof Make the triangular numbers 1 st 1 2 nd 1 + 2 3 rd 1 + 2 + 3 4 th 1 + 2 + 3 + 4 and so on… 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253 406, 425, …

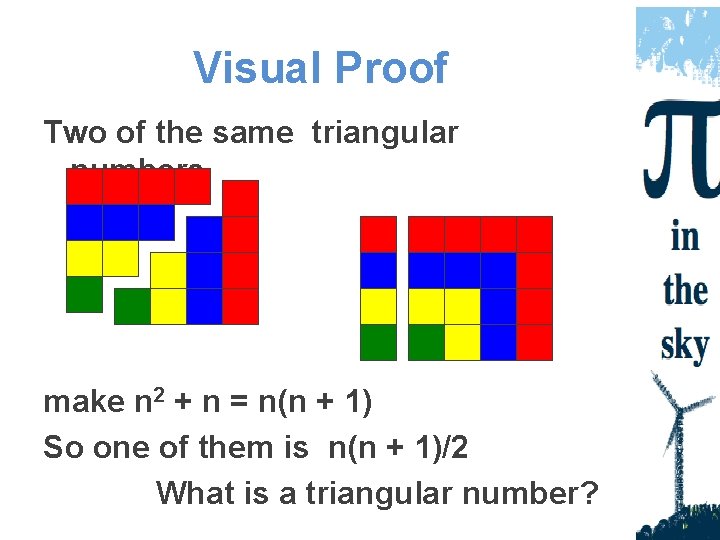
Visual Proof Two of the same triangular numbers make n 2 + n = n(n + 1) So one of them is n(n + 1)/2 What is a triangular number?

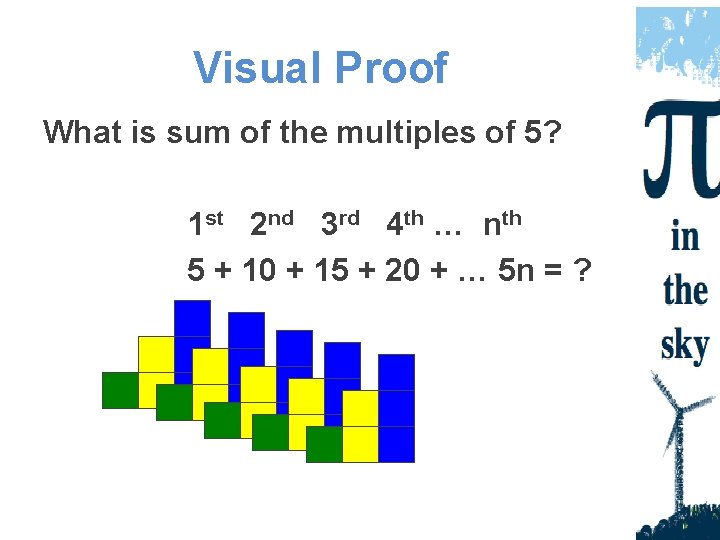
Visual Proof What is sum of the multiples of 5? 1 st 2 nd 3 rd 4 th … nth 5 + 10 + 15 + 20 + … 5 n = ?

Visual Proof Name other applications of this knowledge. See A Triangular Journey

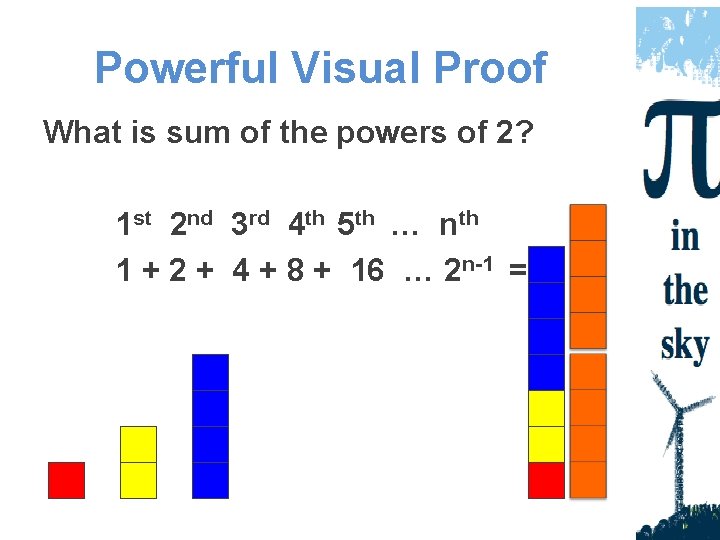
Powerful Visual Proof What is sum of the powers of 2? 1 st 2 nd 3 rd 4 th 5 th … nth 1 + 2 + 4 + 8 + 16 … 2 n-1 = ?

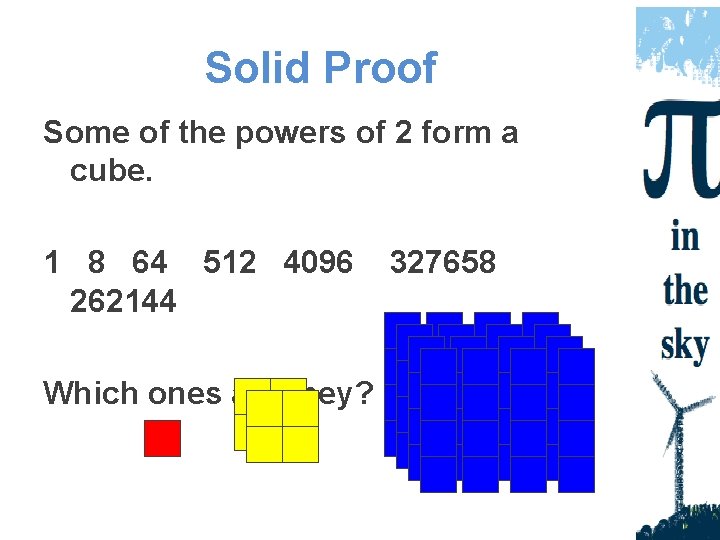
Solid Proof Some of the powers of 2 form a cube. 1 8 64 512 4096 262144 Which ones are they? 327658

An odd look at numbers nth odd is 2 n -1 1 + 3 + 5 + 7 + … (2 n-1) Notice (2 n-1) = (n-1) + n. The odd numbers are consecutive pairs 0+1, 1+2, 2+3, 3+4, 4+5, 5+6, …

Proof by Induction The idea is easy. Prove the first is true. Show for any one k… the truth Prove for the next one, k + 1… the truth By a dominoe effect if 1 is true then so is 2 and 3 and 4 and 5 and …so on.

Proof by Induction Odd numbers are consecutive pairs 0+1, 1+2, 2+3, 3+4, 4+5, 5+6, … nth odd number = (n – 1) + n Eg, n = 3, makes 3 – 1 + 3 = 2 + 3 = 5 When n = k, this makes k – 1 + k = 2 k -1 Put n = k + 1, makes k + 1 – 1 + k + 1 = 2 k + 1

Prove the sum of the odd numbers is n 2. When n = 1, n 2 is 1 When n = k, n 2 is k 2 When n = k + 1, k 2 is (k+1)2 = k 2 + 2 k + 1 = k 2 + 2 k – 1 +2 We need to see that 2 k – 1 +2 is the next odd number added on… Q. E. D.

Try an Inductive Proof Sum of whole numbers is n(n+1)/2 Sum of even numbers is n(n+1)

# of Vertices = # of Sides What happens when you cut off one of the vertices of a triangle? What the students may not realise is that they have performed a proof by induction.

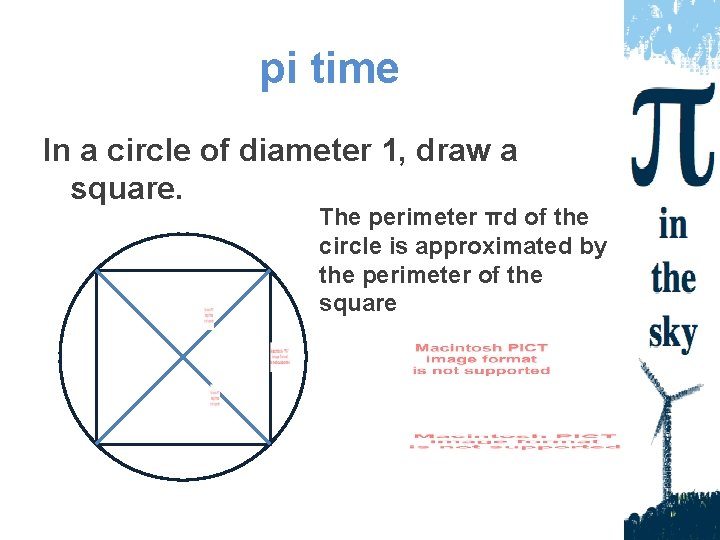
pi time In a circle of diameter 1, draw a square. The perimeter πd of the circle is approximated by the perimeter of the square

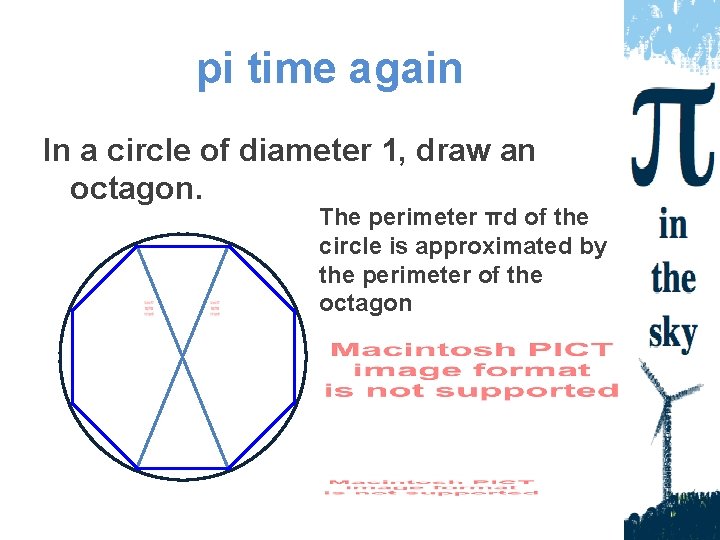
pi time again In a circle of diameter 1, draw an octagon. The perimeter πd of the circle is approximated by the perimeter of the octagon

The nine digits problem The digits 1 to 9 have to go into the nine boxes, with no repeats. + = – = × =

The nine digits problem Here is one possible solution. 1 + 7 =8 9– 4=5 2× 3=6 Is there another?

Here a few solutions And digits can be swapped between equations. 1+7=8 7+1=8 4+5=9 4+ 5=9 9– 4=5 8– 7=1 8– 1= 7 2× 3=6 Why is 2 x 4 = 8 not an option?

The nine digits problem If three even digits are used in the multiplication, there are not enough even digits left for the addition and the subtraction. Ex. E=E O+O=E O – O = uh uh This is called “parity checking”.

That’s it Folks This file is on my website http: //schools. reap. org. nz/advisor jimhogan@clear. net. nz Clearly labelled for you. There a few extra files from Paul and references to his website http: //www. learningnetwork. ac. nz/

We could make a conjecture (Latin “throw together”) Or could experiment with a supposition (Latin “place under” & “location”) Or form an hypothesis (Greek “under” & “foundation”)

n 2 is the sum of the first n odd numbers n 1 2 3 4 … k k+1 2 n – 1 1 3 5 7 … 2 k - 1 2(k + 1) - 1 n 2 1 4 … k 2 ? ? = k 2 + 2(k+ 1) - 1 = k 2 + 2 k+ 2 - 1 = k 2 + 2 k = ( k + 1)2 + 1

n 2 is the sum of the first n odd numbers n 1 2 3 4 … k 2 n – 1 1 3 5 7 … 2 k - 1 n 2 1 4 … The total of the middle row is 1 + 3 + 5 + … + 2 k-5 + 2 k-3 + 2 k-1 = 1 + 2 k-1 + 3 + 2 k-3 + 5 + 2 k-5 + … = 2 k + … = 2 k × k/2 = k 2

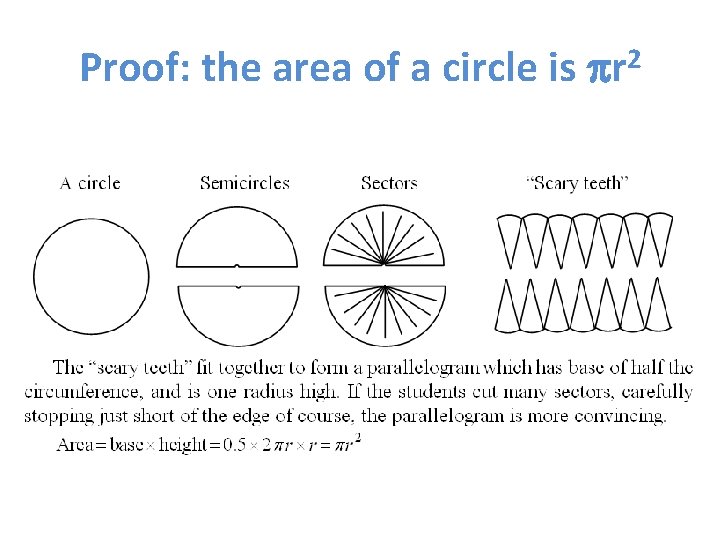
Proof: the area of a circle is r 2

Proof: sum of interior angles of a triangle is 180

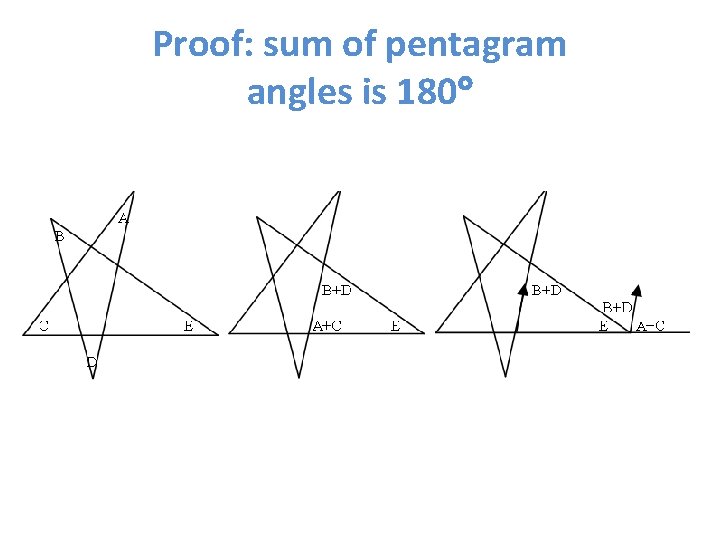
Proof: sum of pentagram angles is 180

Answers to other “Challenges” A. For any two numbers, the sum of their squares is never less than twice their product. (a – b)2 0 a 2 – 2 ab + b 2 0 a 2 + b 2 2 ab Some people like to write Q. E. D. to mark the end of the proof. It is Latin, quod erat demonstrandum and means “Hooray! I’ve finished the proof!”. What Q. E. D. does not stand for is “Quite Easily Done”!

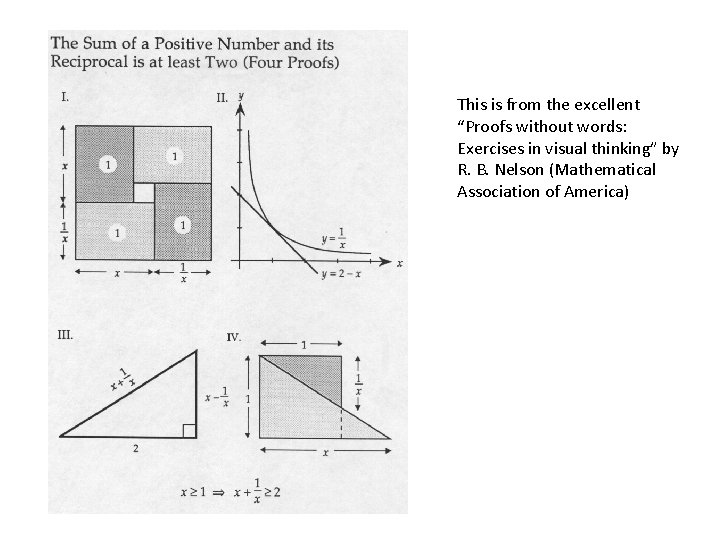
Answers to other “Challenges” B. The sum of any positive number and its reciprocal is 2 or greater.

This is from the excellent “Proofs without words: Exercises in visual thinking” by R. B. Nelson (Mathematical Association of America)

Answers to other “Challenges” C. If the final score is a draw, the number of possible half-time scores is a square. This is from the “Squares” CD-ROM.

Answers to other “Challenges” D. The product of any two Hilbert numbers is a Hilbert number. The Hilbert numbers are 1, 5, 9, 13, 17, 21, 25, . . . They are the numbers one greater than numbers in the four times table. For n = 1, 2, 3, 4, 5, 6, . . . the Hilbert numbers are 4 n + 1. Let the two numbers be 4 x + 1 and 4 y + 1 where x and y are natural numbers. The product = (4 x + 1) (4 y + 1) = 16 xy + 4 x + 4 y + 1 = 4(4 xy + x + y) + 1 which is a Hilbert number.

Paul Brown can be contacted at pbperth@gmail. com