Proof of Kleinbergs smallworld theorems Kleinbergs SmallWorld Model

Proof of Kleinberg’s small-world theorems

Kleinberg’s Small-World Model Consider an (n x n) grid. Each node has links to every node at lattice distance p (short range neighbors) & q long range links. Choose long-range links s. t. the prob. to have a long range contact at lattice distance d is proportional to 1/dr n p = 1, q = 2 r = 2 n Recall Kleinberg’s results. Is there a justification?

Results Theorem 1 There is a constant α 0 (depending on p and q but independent of n), so that when r = 0, the expected delivery time of any decentralized algorithm is at least α 0. n 2/3

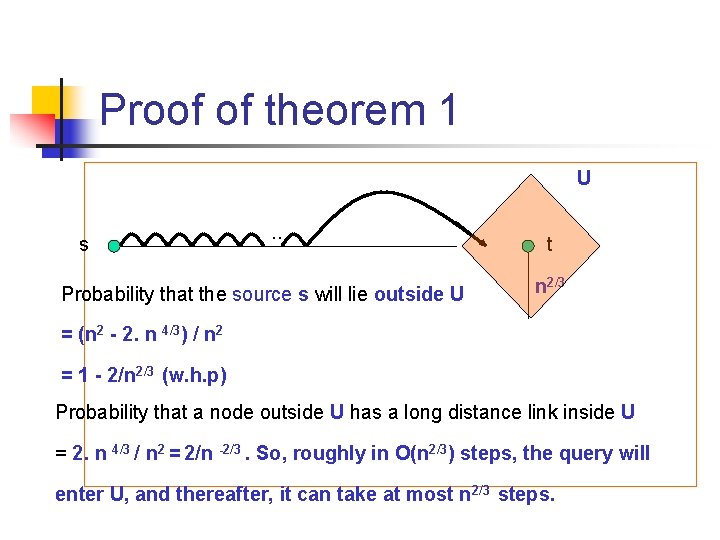
Proof of theorem 1 U s . . Probability that the source s will lie outside U t n 2/3 = (n 2 - 2. n 4/3) / n 2 = 1 - 2/n 2/3 (w. h. p) Probability that a node outside U has a long distance link inside U = 2. n 4/3 / n 2 = 2/n -2/3. So, roughly in O(n 2/3) steps, the query will enter U, and thereafter, it can take at most n 2/3 steps.

Results Theorem 2. There is a decentralized algorithm A and a constant α 2 dependent on p and q but independent of n, so that when r = 2 and p = q = 1, the expected delivery time of A is at most α 2. (log n)2

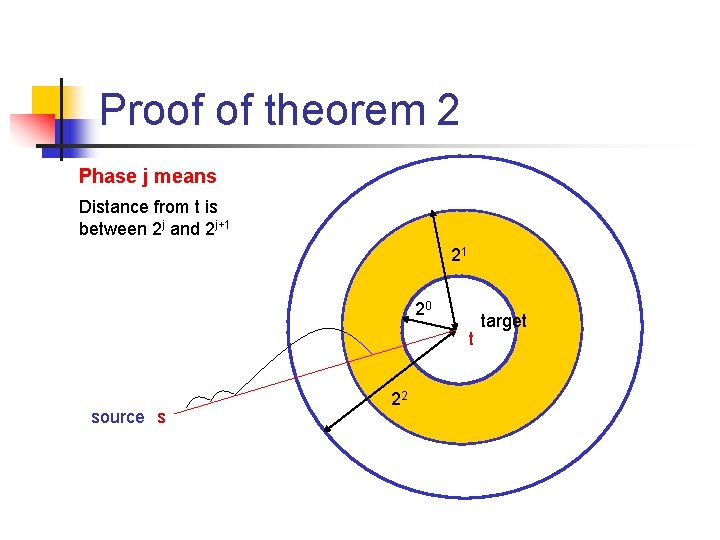
Proof of theorem 2 Phase j means Distance from t is between 2 j and 2 j+1 21 20 t source s 22 target

Observation How many nodes are at a lattice distance j from a given node? 4. j How many nodes are at a lattice distance j or less from a given node? 1 + 4. j + 4. (j-1) + 4. (j-2) + … = 1 + 4. j. (j+1)/2 = 1 + 2. j. (j+1) = 1 + 2 j 2 + 2 j

Proof Main idea We show that in phase j, the expected no of hops before the current message holder discovers a longrange contact within lattice distance 2 j of t is O(log n); After this, phase j comes to an end. As there at most log n phases, a bound proportional to log 2 n follows.

Proof Probability (node u chooses node v as its long-range contact) is But So, the probability (u chooses v) is There are 4 j nodes at distance j

Proof Phase j 2 j+1 ≤ (distance to v) < 2 j The maximum value of j is log 2 n (⋍ log n) When will phase j end? What is the prob that it will end in the next step? Zone Bj consists Of all nodes within Lattice distance 2 j from the target v No of nodes in Zone Bj is u each within distance 2 j+1 + 2 j < 2 j+2 from a node like u

Proof So each has a probability of of being a long-distance contact of u, So, the search enters Bj with a probability of at least Zone Bj consists Of all nodes within Lattice distance 2 j from the target v u So, the expected number of steps spent in phase j is 128 ln (6 n). Since There at most log n phases, the Expected time to reach v is O(log n)2