Proof by Contradiction Discrete Structures CS 173 Adapted

Proof by Contradiction Discrete Structures (CS 173) Adapted from Derek Hoiem, University of Illinois 1

Proof by Contradiction • 2

Contradiction • 3

Proof by contradiction Claim: There are infinitely many prime numbers Equivalent claim: There is not a finite set of primes. 4

Basic form of proof by contradiction • 5

Why proof by contradiction works • 6

Another explanation • 7

Danger of proof by contradiction: a mistake in the proof might also lead to a contradiction See this blog post about P=NP problem http: //rjlipton. wordpress. com/2011/01/08/proofs-by-contradiction-and-other-dangers/ 8

Proof by contradiction • 9

Proof by contradiction Claim: No lossless compression algorithm can reduce the size of every file. 10

Why image compression works: images are mostly smooth

Proof by contradiction Claim: A cycle graph with an odd number of nodes is not 2 colorable. 12

Proof by contradiction or contrapositive • 13

When to use each type of proof Match the situation to the proof type Situation 1. Can see how conclusion directly follows from hypothesis 2. Need to demonstrate claim for an unbounded set of integers 3. Easier to show that negation of hypothesis follows from negation of conclusion 4. Need to show that something doesn’t exist 5. Need to show that something exists Proof type a) Direct proof b) Proof by example or counter-example c) Proof by contrapositive (or logical equivalence) d) Induction e) Proof by contradiction 14

When to use each type of proof Match the situation to the proof type Situation 1. Can see how conclusion directly follows from claim (a) 2. Need to demonstrate claim for an unbounded set of integers (d) 3. Easier to show that negation of hypothesis follows from negation of conclusion (c) 4. Need to show that something doesn’t exist (e) 5. Need to show that something exists (b) Proof type a) Direct proof b) Proof by example or counter-example c) Proof by contrapositive (or logical equivalence) d) Induction e) Proof by contradiction 15

When to use each type of proof Match the claim to the suitable proof type • Proof type a) Direct proof b) Proof by example or counter-example c) Proof by contrapositive (or logical equivalence) d) Induction e) Proof by contradiction 16

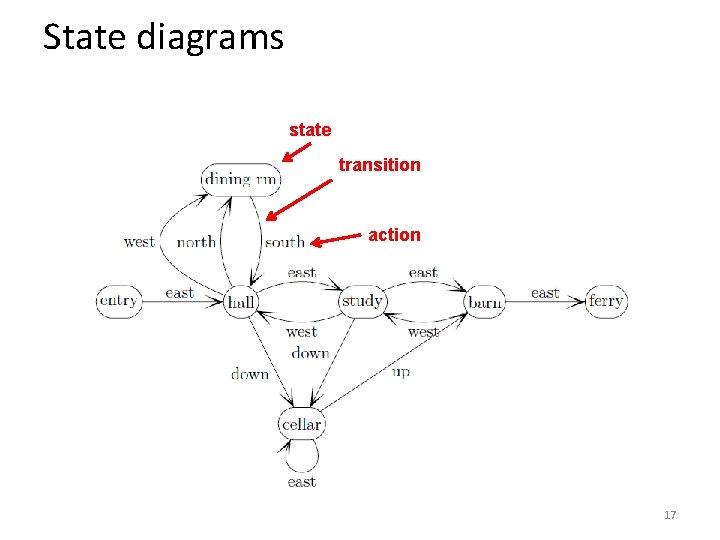
State diagrams state transition action 17

Simple example: traffic signal 18

Transition functions and state diagrams States: Village, Rock, Snake, Chasm, Gold, Desert Transitions: (Village, North) Desert (Village, East) Snake (Desert, South) Village (Desert, East) Rock (Rock, West) Desert (Snake, West) Village (Snake, East) Chasm (Snake, South) Gold (Gold, North) Snake 19

Transition functions and state diagrams Input sequence to beat the game: N, E, E, N, W, GET ROCK, N, W, N, THROW ROCK, N, DRINK WATER, E, GET STICK, THROW STICK, W, N, THROW STICK, LOOK HOLE, GET NOTE, N, W, LIFT ROCK, N, GET NOTE, E, GET LOCKET, E, E, S, W, W, LOOK HOLE, GET CRACKER, E, N, N, W, N, SAY HOCUS, N, GO HOUSE, GET APPLE, W, N, LOOK GNOME, N, E, SAY HISS, GO CREVICE, S, S, S, GET BREAD, GET LOCKET, GET CRACKER, UNLOCK DOOR, OPEN DOOR, GO DOOR, U, GO HOLE, N, E, S, GIVE CRACKER, GET VIAL, N, W, S, W, W, THROW BREAD, N, GET ROPE, GO BOAT USE BLANKET, N, N, DRINK WATER, N, E, E, E, GO BEACH, N, N, E, GET ANCHOR, W, TIE ROPE, TO ANCHOR, THROW ANCHOR, UP, GET SHOVEL, DOWN, S, S, DIG X, LOOK TREASURE, GRAB CHEST, LEAVE, E, N, W, GO CAVE, OPEN CHEST, LOOK CHEST, GET HARP, N, E, N, DRINK VIAL, FLY NORTH, N, GET RING, N, W, FOLLOW RAINBOW, GET COIN, N, SAY LUCY, W, W, N, GO CAVE, GET ALL, N, S, W, PLAY HARP, N, N, BUY HORN, N, N, BLOW HORN, N, U, E, OPEN CLOSET, LOOK CLOSET, GET SHOES, LOOK SHOES, W, D, W, W, LOOK THRONE, THROW APPLE, N, E, LOOK CABINET, PICK LOCK, WITH KNIFE, OPEN DOOR, E, U, D, U, WEAR RING, RUB RING, D, E, KISS FROG, WEAR SHOES, SAY WHOOSH Adventures in Serenia 20