Promoting Mathematical Thinking University of Oxford Dept of























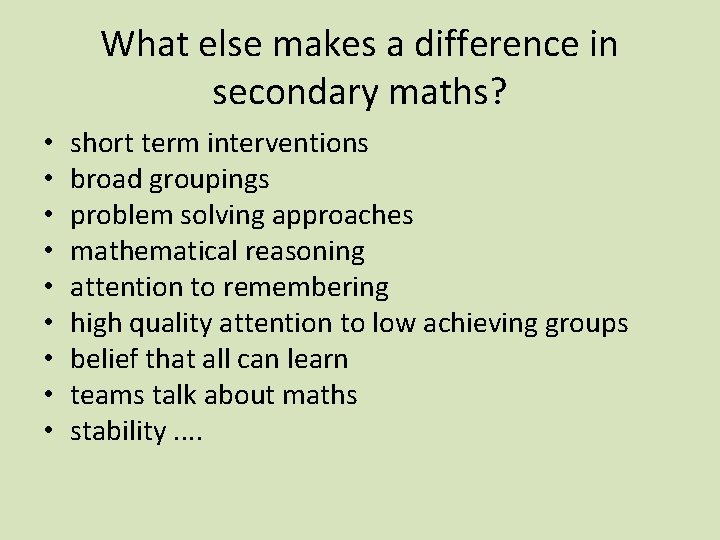

- Slides: 30
Promoting Mathematical Thinking University of Oxford Dept of Education What makes a difference in secondary maths? Bucks, Berks and Oxon Maths Hub 23 June 2015 High Wycombe

Plan • common threads about effective teaching from research • opportunities from NC (problem-solving) • some examples

Comparative research within UK says: • ability grouping hinders most students • short term targeted intervention helps • problem solving teaching is more effective for dealing with unfamiliar questions, and does no harm for standard questions • ICT can aid access to harder topics earlier • ‘force-fed’ students do less well at A level and university than deeper learners

Longitudinal study (14000) in UK says: • mathematical reasoning and arithmetic are both important • mathematical reasoning is more important than arithmetic at KS 2 and 3 • spatial reasoning is important, but less so than mathematical reasoning and arithmetic • focusing and remembering are important • setting hinders most students • high SES do better than low SES and boys do better than girls

International comparisons say: • What matters is: – mathematical coherence (concepts develop meaningfully) – pedagogical coherence (students know why they are doing things; what the norms are; how it all links together) – conceptual work on meanings and ideas as well as procedural and applications – mathematical reasoning, conjecturing, generalisation in most lessons – complex situations stay complex – students are engaged and motivated

Successful teaching for all in UK shows: • belief in, and commitment to, the learning of all students • teams talk about maths • stability of teachers and students helps • affirmation – students know the value of what they are learning

Affirmation How sure can we be about this new idea? Why does this new idea matter? What does it do for me? How is it represented? How can it be adapted/transformed? How does it apply to more complex maths/other contexts? • How did we get here? • • •

Affirmation • Specialist teachers focused on rigour, abstraction of ideas, use and connections within mathematics • Non-specialist teachers focused on use outside mathematics (sometimes spurious) and exams

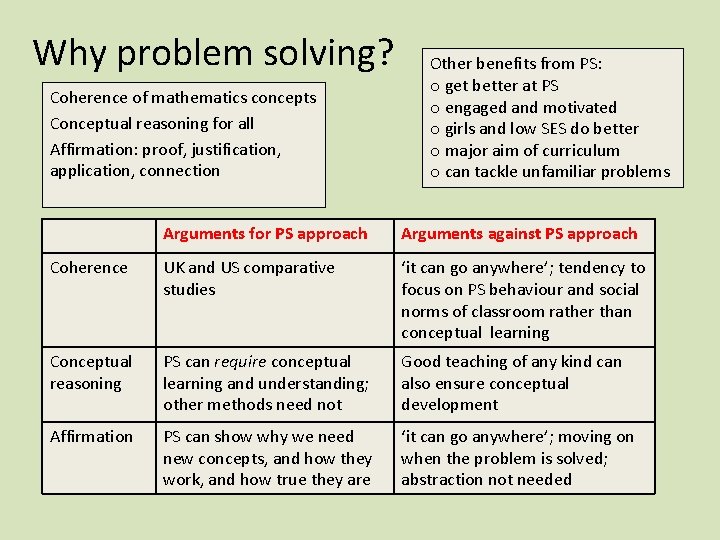
Common threads from all research sources, local and global: • Coherence of mathematics concepts • Conceptual reasoning for all • Affirmation: proof, justification, application, connection

Why problem solving? Coherence of mathematics concepts Conceptual reasoning for all Affirmation: proof, justification, application, connection Other benefits from PS: o get better at PS o engaged and motivated o girls and low SES do better o major aim of curriculum o can tackle unfamiliar problems Arguments for PS approach Arguments against PS approach Coherence UK and US comparative studies ‘it can go anywhere’; tendency to focus on PS behaviour and social norms of classroom rather than conceptual learning Conceptual reasoning PS can require conceptual learning and understanding; other methods need not Good teaching of any kind can also ensure conceptual development Affirmation PS can show why we need new concepts, and how they work, and how true they are ‘it can go anywhere’; moving on when the problem is solved; abstraction not needed

What does problem solving mean? • Application after learning new technique – Is this really problem solving, or templating? • Exploring a new idea within a problem, to give it meaning and purpose – Find its power, limits, behaviour • To create a need for a new idea – Earlier knowledge goes some way towards it, but you need more • To get better at problem solving in general – Is there time for this as a separate focus?

Example of a lesson to prove angle sum of triangle (Japan) • Ninja knowledge • Can we apply any Ninja knowledge to this diagram? • What can we add to this diagram to use more Ninja knowledge? (parallel lines) • Erase unhelpful Ninja knowledge • Apply helpful Ninja knowledge • Share methods and discuss

NC KS 3/4 random dips “use algebra to generalise the structure of arithmetic, including to formulate mathematical relationships” ?

Structure of arithmetic • Coherence? • Conceptual reasoning? • Affirmation?

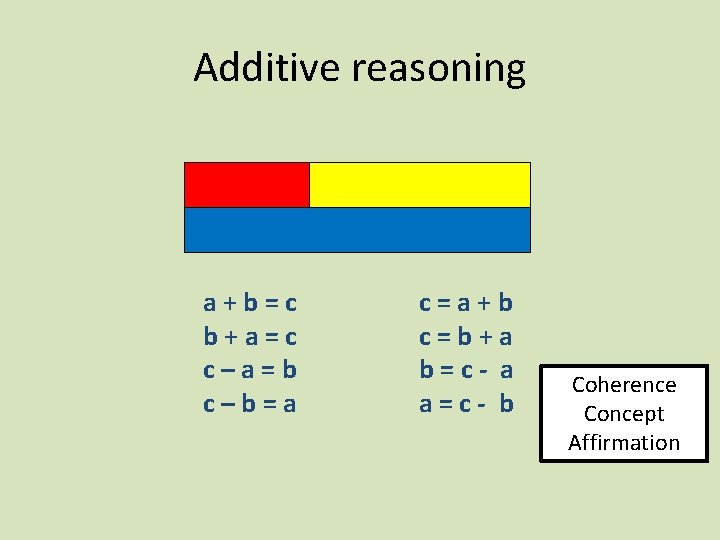
Additive reasoning a+b=c b+a=c c–a=b c–b=a c=a+b c=b+a b=c- a a=c- b Coherence Concept Affirmation

Multiplicative reasoning a = bc a = cb b=a c c=a b bc = a cb = a a=b c a=c b Coherence Concept Affirmation

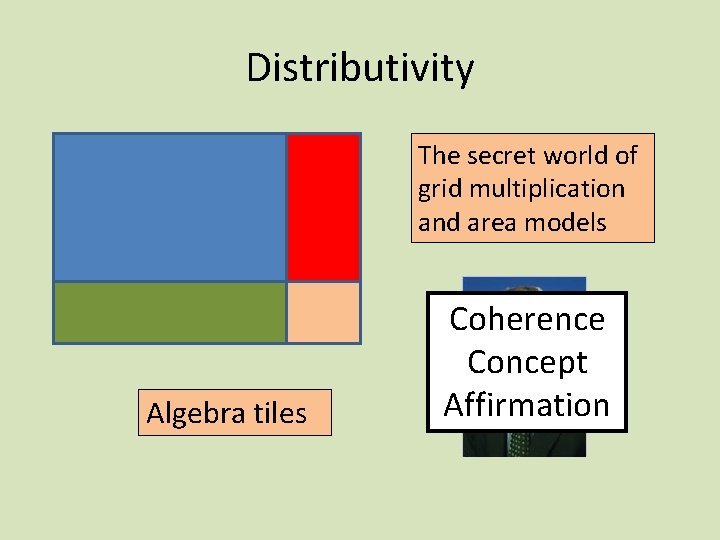
Distributivity The secret world of grid multiplication and area models Algebra tiles Coherence Concept Affirmation

What about algebraic manipulation? • • • Additive relationship Multiplicative relationship Distributive law Inverse operations The meaning of equality Coherence Concept Affirmation

Let h be the height and b be the base measurements of a triangle, and A be its area. A = h/2 x b A=bxh÷ 2 A = m x h/2 + n x h/2 where m+n=b

Another random dip. . . • develop algebraic and graphical fluency, including understanding linear and simple quadratic functions – Coherence? – Conceptual reasoning? – Affirmation? http: //www. teachmathematics. net/page/9673/quadratic-movers

Rationale for quadratics in the curriculum • Area l- 2 A = l(l-2) y = a (x-b)(x-c) l • Not-proportional; varying rate of change; an accessible non-linear relationship Coherence • Reason for algebraic manipulation Concept • Social pressure Affirmation

More random dips. . . “divide a given quantity into two parts in a given part: part or part: whole ratio” “understand that a multiplicative relationship between two quantities can be expressed as a ratio or a fraction” “relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions” – Coherence? – Conceptual reasoning? – Affirmation?

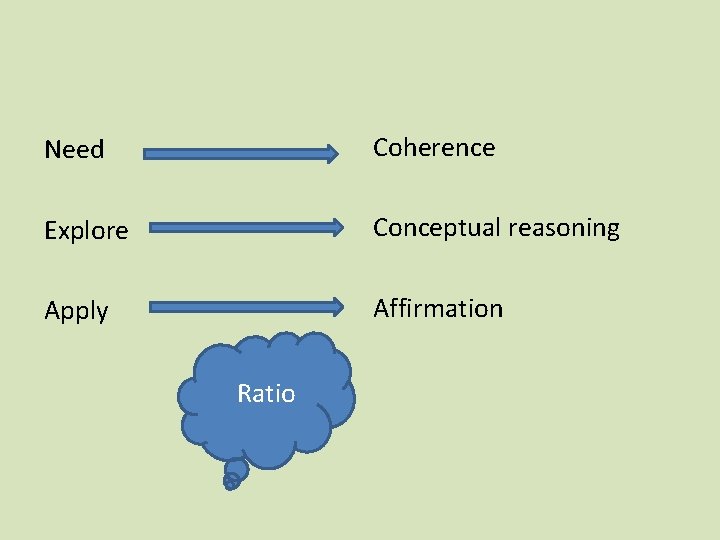
Why take a problem-solving approach? “relate ratios to arithmetic • Apply a new technique of fractions and to • Explore a new idea linear functions” • Need a new idea – Coherence? – Conceptual reasoning? – Affirmation? Need – Explore – Apply Coherence – Conceptual reasoning – Affirmation

Ratios, fractions, linear functions. . . • Need. . . . ? • Explore. . . . ? • Apply. . . . ? Currency exchange rates k = x/y sharing costs and finished products of a collaborative. Relating lengths cooking event in families of similar triangles

Need Coherence Explore Conceptual reasoning Apply Affirmation Ratio

Another random dip. . . KS 3 Exponential powers. . “Find approximate solutions to contextual problems from exponential graphs” KS 4 (bold) Exponential functions “Recognise, sketch and interpret graphs of the exponential function for positive values of k”

Need Coherence Explore Conceptual reasoning Apply Affirmation Exponential powers, graphs and functions

What makes a difference in secondary maths? Need Coherence Explore Conceptual reasoning Apply Affirmation Embedding these throughout mathematics
What else makes a difference in secondary maths? • • • short term interventions broad groupings problem solving approaches mathematical reasoning attention to remembering high quality attention to low achieving groups belief that all can learn teams talk about maths stability. .

Promoting Mathematical Thinking University of Oxford Dept of Education anne. watson@education. ox. ac. uk
 Continuing education library oxford
Continuing education library oxford Promoting alternative thinking strategies
Promoting alternative thinking strategies Mathematical sciences oxford
Mathematical sciences oxford Non mathematical economics
Non mathematical economics Oxford university press south africa
Oxford university press south africa Oxford university press answer
Oxford university press answer M.swan (oxford university press)
M.swan (oxford university press) Oxford university safety office
Oxford university safety office Strlen( oxford university press ) is
Strlen( oxford university press ) is Oxford university press malaysia
Oxford university press malaysia Webmail oxford
Webmail oxford Ouccc
Ouccc Oxford university press
Oxford university press Dropping out of oxford
Dropping out of oxford Oxford university press
Oxford university press Positive thinking vs negative thinking examples
Positive thinking vs negative thinking examples Thinking about your own thinking
Thinking about your own thinking Holistic judgement
Holistic judgement Perbedaan critical thinking dan creative thinking
Perbedaan critical thinking dan creative thinking Thinking about you thinking about me
Thinking about you thinking about me Dept nmr spectroscopy
Dept nmr spectroscopy Fl dept of agriculture
Fl dept of agriculture Finance dept structure
Finance dept structure Inspectors in worcester
Inspectors in worcester Dept. name of organization (of affiliation)
Dept. name of organization (of affiliation) Mn dept of education
Mn dept of education Department of finance and administration
Department of finance and administration Dept. name of organization
Dept. name of organization Ohio dept of developmental disabilities
Ohio dept of developmental disabilities Poster affiliation
Poster affiliation Vaginal dept
Vaginal dept