Promoting Mathematical Thinking Fraction Actions Working with Fractions

Promoting Mathematical Thinking Fraction Actions: Working with Fractions as Operators John Mason Calgary Oct 2014 1 The Open University Maths Dept University of Oxford Dept of Education

What Does it Mean? 3 divided by 5 Divide 3 by 5 The answer on dividing 3 by 5 The action of ‘three fifth-ing’ The result of ‘three fifth-ing’ of 1 on the numberline The value of the ratio of 3 to 5 The equivalence class of all fractions with value three fifth’s (a number) Place on the number line (number) … 2

Different Perspectives v v v 3 What is the relation between the numbers of squares of the two colours? Difference of 2, one is 2 more: additive thinking Ratio of 3 to 5; one is five thirds the other etc. : multiplicative thinking

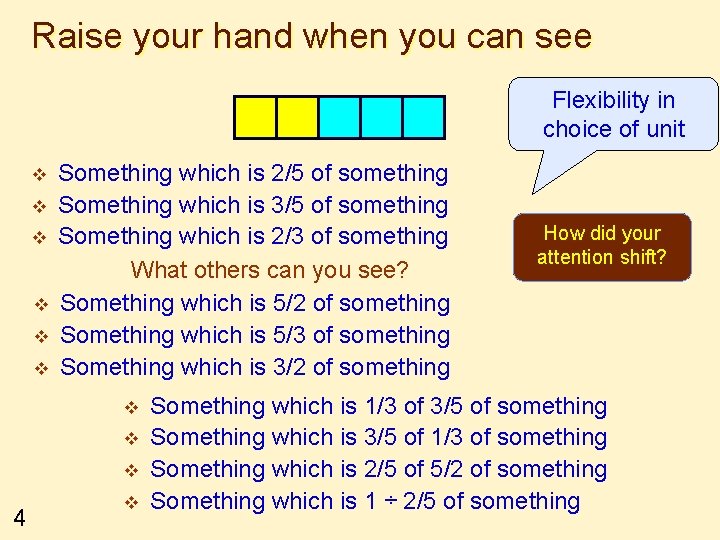
Raise your hand when you can see Flexibility in choice of unit v v v Something which is 2/5 of something Something which is 3/5 of something Something which is 2/3 of something What others can you see? Something which is 5/2 of something Something which is 5/3 of something Something which is 3/2 of something v v v 4 v How did your attention shift? Something which is 1/3 of 3/5 of something Something which is 3/5 of 1/3 of something Something which is 2/5 of 5/2 of something Something which is 1 ÷ 2/5 of something

Doing & Undoing v v What operation undoes ‘adding 3’? What operation undoes ‘subtracting 4’? What operation undoes ‘subtracting from 7’? What are the analogues for multiplication? v What undoes ‘multiplying by 3’? v What undoes ‘dividing by 4’? v v 5 What undoes ‘multiplying by ¾’? v Two different expressions! What operation undoes ‘dividing into 24’?

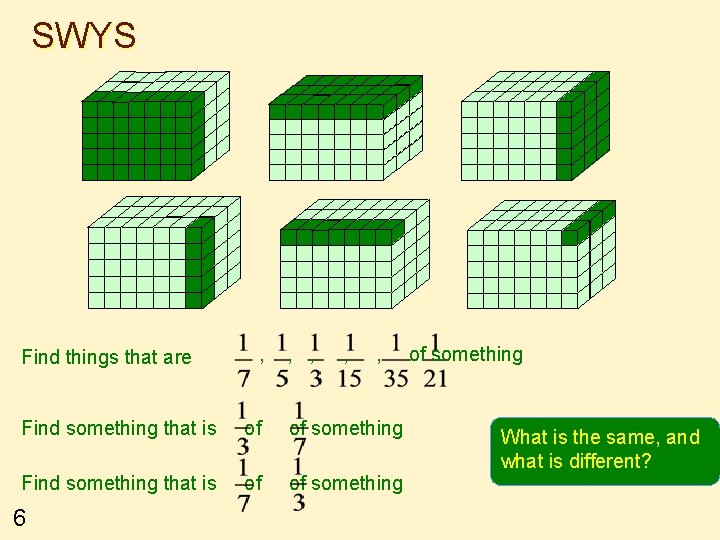
SWYS Find things that are , , , Find something that is of of something 6 of something What is the same, and what is different?

Presenting Fractions as Actions 7

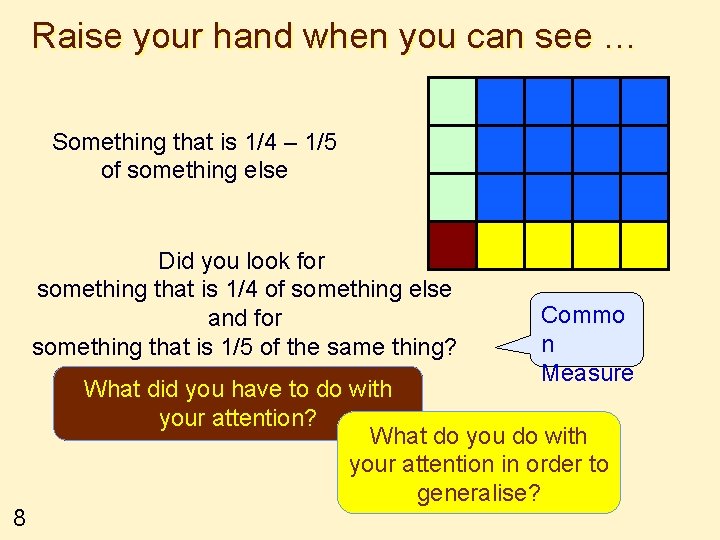
Raise your hand when you can see … Something that is 1/4 – 1/5 of something else Did you look for something that is 1/4 of something else and for something that is 1/5 of the same thing? 8 Commo n Measure What did you have to do with your attention? What do you do with your attention in order to generalise?

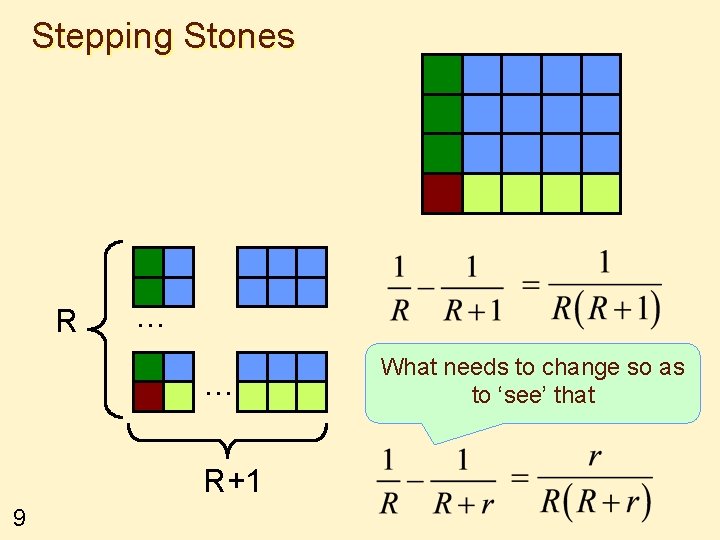
Stepping Stones R … … R+1 9 What needs to change so as to ‘see’ that

Elastic Multiplication 10

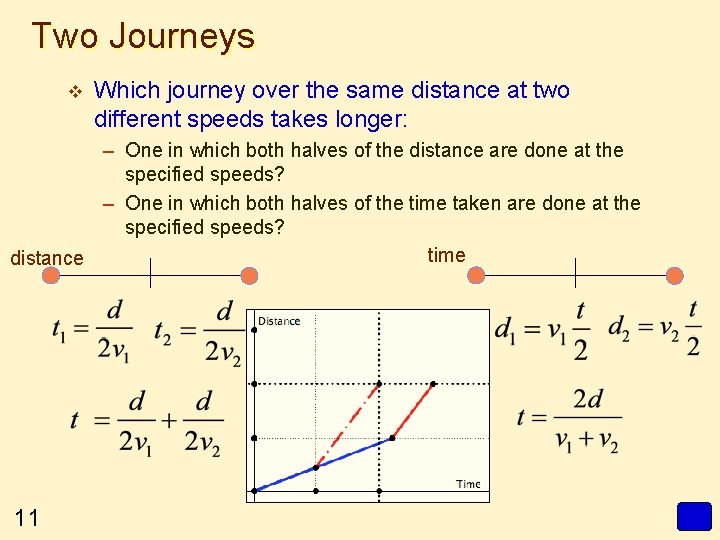
Two Journeys v Which journey over the same distance at two different speeds takes longer: – One in which both halves of the distance are done at the specified speeds? – One in which both halves of the time taken are done at the specified speeds? time distance 11

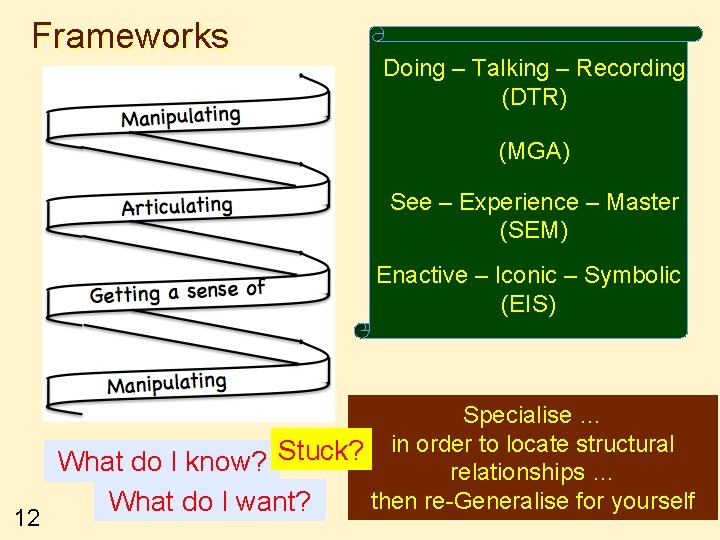
Frameworks Doing – Talking – Recording (DTR) (MGA) See – Experience – Master (SEM) Enactive – Iconic – Symbolic (EIS) 12 Specialise … in order to locate structural Stuck? What do I know? relationships … then re-Generalise for yourself What do I want?

Mathematical Thinking v v 13 How describe the mathematical thinking you have done so far today? How could you incorporate that into students’ learning?

Possibilities for Action v v v 14 Trying small things and making small progress; telling colleagues Pedagogic strategies used today Provoking mathematical thinking as happened today Question & Prompts for Mathematical Thinking (ATM) Group work and Individual work

Human Psyche Awareness (cognition) Imagery Will Emotions (affect) Body (enaction) Habits Practices 15

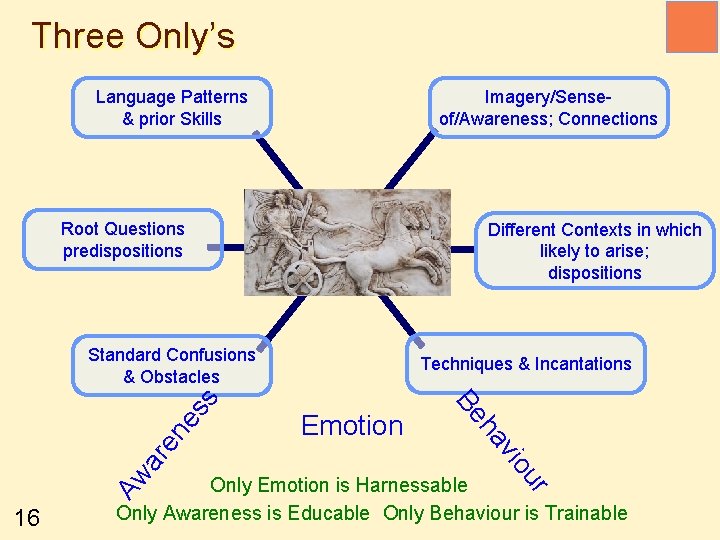
Three Only’s Language Patterns & prior Skills Imagery/Senseof/Awareness; Connections Root Questions predispositions Different Contexts in which likely to arise; dispositions en ar Aw Emotion io av Only Emotion is Harnessable Only Awareness is Educable Only Behaviour is Trainable ur 16 Techniques & Incantations h Be es s Standard Confusions & Obstacles

Follow Up v v v v 17 j. h. mason @ open. ac. uk mcs. open. ac. uk/jhm 3 Presentations Questions & Prompts (ATM) Key ideas in Mathematics (OUP) Learning & Doing Mathematics (Tarquin) Thinking Mathematically (Pearson) Developing Thinking in Algebra (Sage)