Promoting Mathematical Thinking Algebra Expressing Generality Interpreting Diagrams

Promoting Mathematical Thinking Algebra Expressing Generality & Interpreting Diagrams The Open University Maths Dept 1 John Mason PTI Haringey 2014 University of Oxford Dept of Education

Conjectures and Assumptions v v v 2 Everything said here is a conjecture … …to be tested in your experience! Enjoyment (in mathematics) arises from acts … … the exercise of internalised skill … the use of natural powers … the development of those powers What you get from this talk is most likely what you notice happening inside you, in order to be sensitised to what learners may be experiencing

Matched Array v v v 3 In how many different ways can you find how many matchsticks would be needed to make an array like this with 16 columns and 12 rows? Could exactly the same number of matchsticks be used to make a different sized array? Generalise! How many vertices does the array have, and how many squares? (Check: Vertices – Matchsticks + Squares = 1)

Matched Array v v I how many different ways can you work out how many matchsticks would be needed to make an array like this with 16 columns and 12 rows? Could exactly the same number of matchsticks be used to make a different sized array? Generalise! Suppose r rows and c columns of squares Then horizontal matches need r(c + 1) matchsticks Vertical matches need c(r + 1) matchsticks Total r(c + 1) + c(r + 1) = 2 rc + r + c So 2 x 16 + 12 + 16 = 412 matchsticks required 4

Undoing v v 5 Suppose N = 2 rc + r + c Then 2 N = 4 rc + 2 r + 2 c 2 N + 1 = (2 r + 1)(2 c + 1) Since 2 x 412 + 1 = 825 = 3 x 5 x 5 x 11, selecting two factors gives … 3 x 11 and 5 x 5 that is 16 rows and 12 columns … 3 x 5 and 5 x 11 that is 7 rows and 27 columns … 3 and 5 x 5 x 11 that is 1 row and 137 columns … 5 and 3 x 5 x 11 that is 2 rows and 82 columns … 11 and 3 x 5 x 5 that is 5 rows and 37 columns

Extensions v v Notice that there are 2 rc + r + c matchsticks rc ‘squares’ (r + 1)(c + 1) vertices So Vertices – Edges + Faces = 1 (Euler) Try putting a diagonal ‘matchstick’ in each square Try three dimensions Try other arrays 6

Sundaram’s Sieve Each row and each column is an arithmetic progression Claim: N will appear in the table iff 2 N + 1 is composite 7 What number will appear in the Rth row and the Cth column?

One Sum v v 8 I have written down two different numbers whose sum is 1. I have squared the larger and added the smaller, and I have squared the smaller and added the larger. Which of my two answers will be the larger?
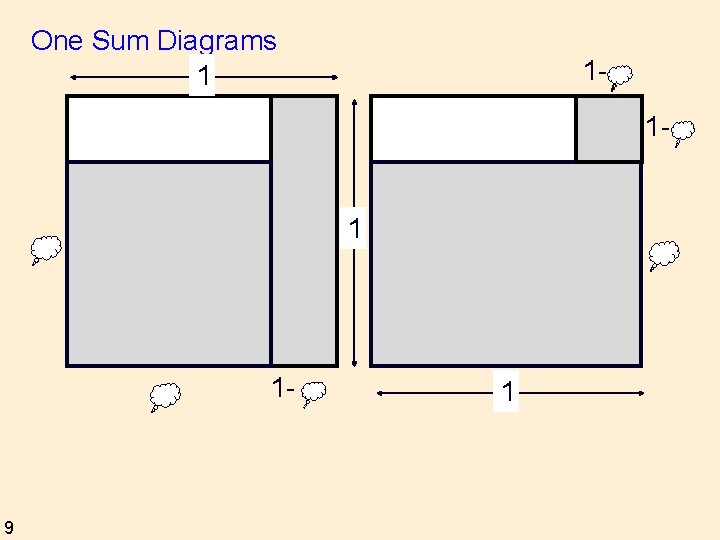
One Sum Diagrams 1 11 - 1 1 - 9 1
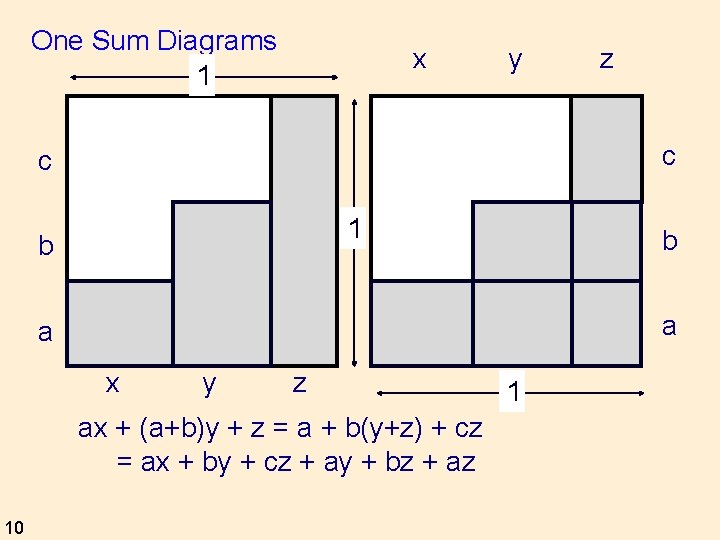
One Sum Diagrams 1 x y c c 1 b b a a x y z ax + (a+b)y + z = a + b(y+z) + cz = ax + by + cz + ay + bz + az 10 z 1
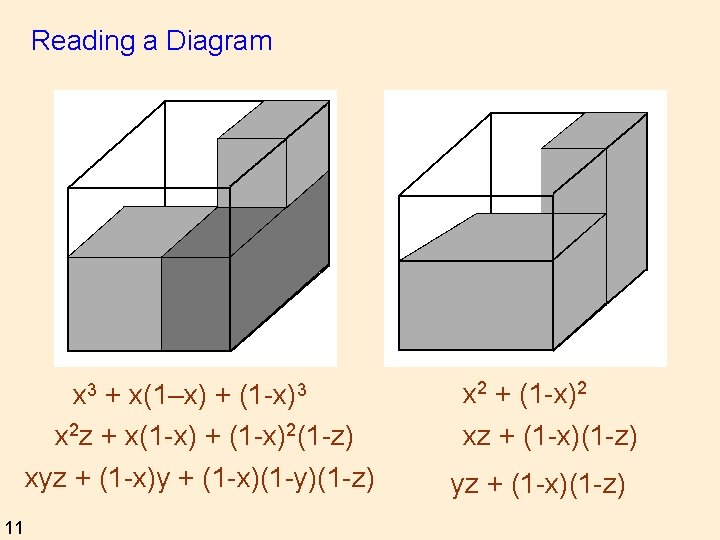
Reading a Diagram x 3 + x(1–x) + (1 -x)3 x 2 z + x(1 -x) + (1 -x)2(1 -z) xyz + (1 -x)y + (1 -x)(1 -y)(1 -z) 11 x 2 + (1 -x)2 xz + (1 -x)(1 -z) yz + (1 -x)(1 -z)

Routes v How many ways are the for getting from the upper left corner to bottom right corner moving only to the right or down along an edge? Denote by r, a move to the right by one edge and by d, a move down one edge Then a journey consist of a sequence of 5 r’s and 3 d’s in some order … Which is the same as the number of terms involving 5 r’s and 3 d’s in the expansion of (r + d)(r + d) (r + d) = (r + d)8 12
13
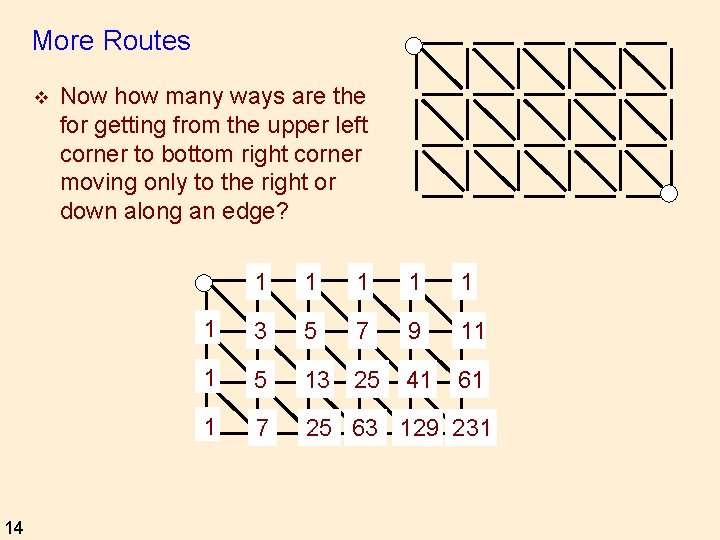
More Routes v 14 Now how many ways are the for getting from the upper left corner to bottom right corner moving only to the right or down along an edge? 1 1 1 3 5 7 9 11 1 5 13 25 41 61 1 7 25 63 129 231
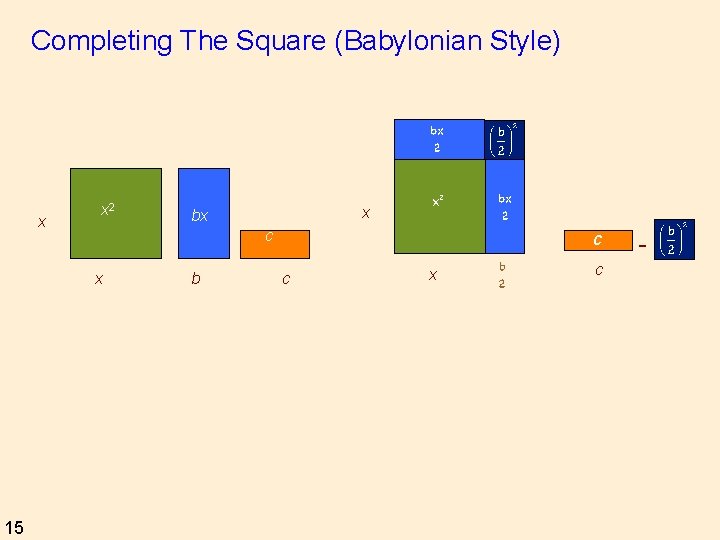
Completing The Square (Babylonian Style) x x 2 c x 15 x bx b c c x c -
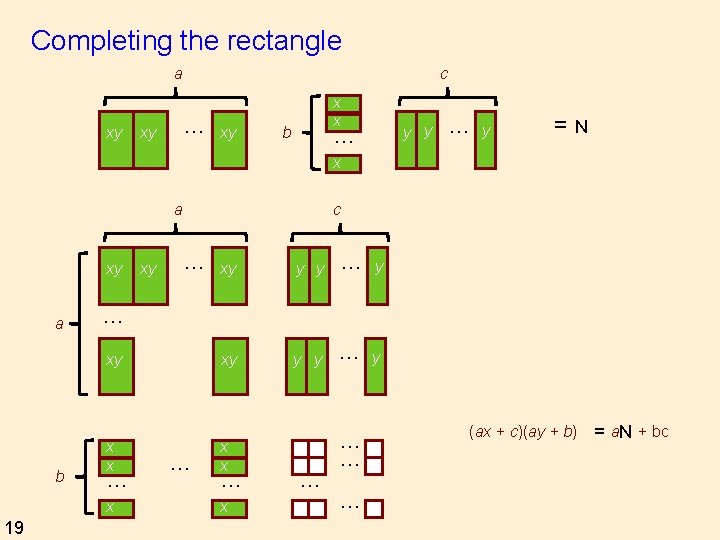
Completing the rectangle a xy c … xy xy x x … b y y … y =N x a xy y y … y xy xy y y … y x x xy a b xy … … … x 19 c … … x … … (ax + c)(ay + b) = a. N + bc

Some Sums 1+2= 3 4+5+6= 7+8 9 + 10 + 11 + 12 = 13 + 14 + 15 16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24 25 + 26 + 27 + 28 + 29 + 30 = 31 + 32 + 33 + 34 + 35 Generalise Justify 20 Say What You See Watch What You Do

1: 2: 3: 4: 5: 1+2= 3 4+5+6= 7+8 9 + 10 + 11 + 12 = 13 + 14 + 15 16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24 25 + 26 + 27 + 28 + 29 + 30 = 31 + 32 + 33 + 34 + 35 : 2 2 Generalise 2 2 + ( +1) + ( +2) +…+( + ) 2 2 2 = ( + +1) + ( + +2) +…+ ( + + ) Justify 21
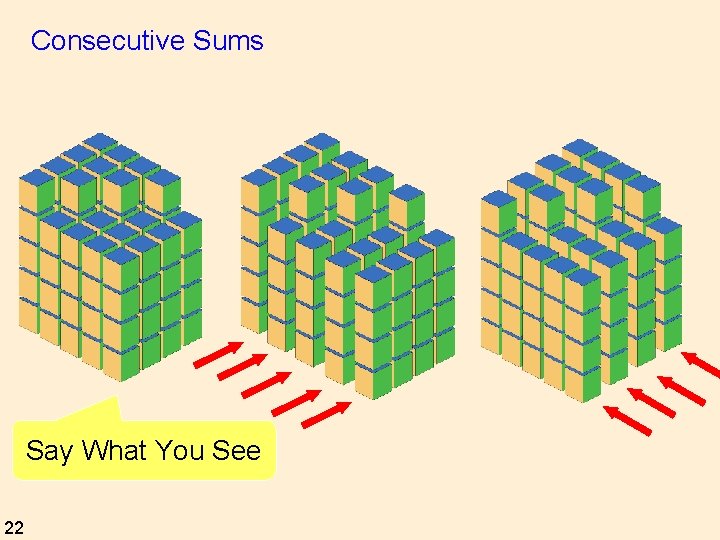
Consecutive Sums Say What You See 22
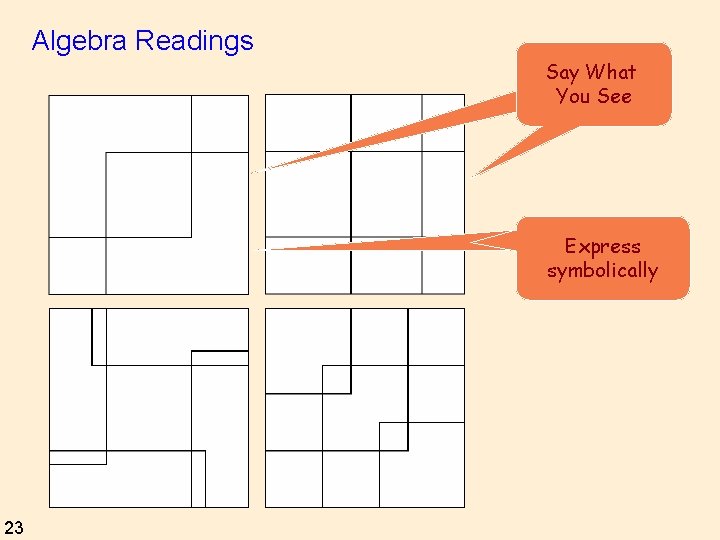
Algebra Readings Say What You See Express symbolically 23

Mutual Factors x 2 + 5 x + 6 = (x + 3)(x + 2) 2 + 5 x – 6 = (x + 6)(x – x 2 x + 13 x + 30 = (x + 10)(x + 3) x 1)2 + 13 x – 30 = (x + 15)(x – 2) x 2 + 25 x + 84 = (x + 21)(x + 4) x 2 + 25 x – 84 = (x + 28)(x – 3) x 2 + 41 x + 180 = (x + 36)(x + 5) x 2 + 41 x – 180 = (x + 45)(x – 4) 24 But there are others!

Follow Up v v v 25 Developing Thinking in Algebra (Sage) Thinking Mathematically (Pearson) Questions & Prompts for Mathematical Thinking (ATM) J. h. mason@open. ac. uk Mcs. open. ac. uk/jhm 3 (presentations; Structured Variation Grids)
- Slides: 22