PROLOG PROgramming in LOGic A Brief Introduction PROLOG

PROLOG PROgramming in LOGic A Brief Introduction ---

PRO-LOG q 1975, Phillippe Roussell q. Predicate Calculus q. Declarative Language q. Predicates and Rules q. Inference Mechanism q. No effective standardization ---

PROLOG Paradigm q PROgramming in LOGic Draw inferences from facts and rules q PROLOG is declarative - specify facts and logical relationships Ø Non-procedural: "what", not "how". Ø Execute the specification. Ø Program execution as theorem proving. Ø Database language with automated search and the ability to follow general rules. symbolic - symbols are used to represent objects high level - contains a built-in problem solving mechanism q PROLOG Programming Declaring some facts about objects and their relationships Defining some rules about objects and their relationships Asking questions about objects and their relationships ---

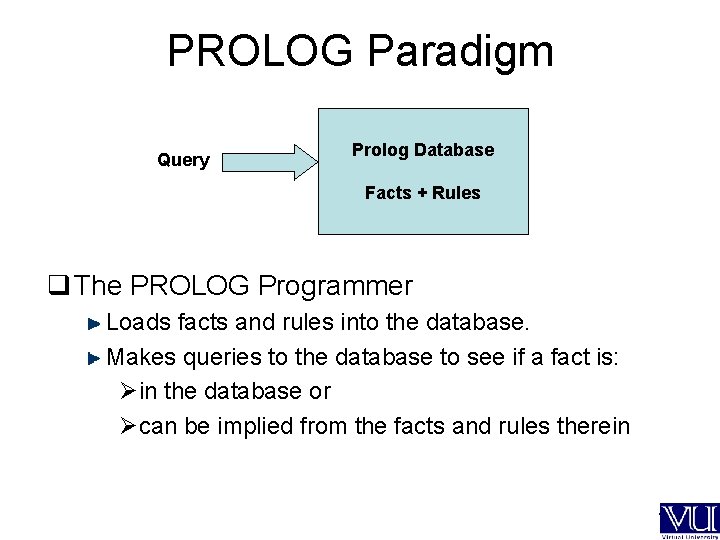
PROLOG Paradigm Query Prolog Database Facts + Rules q The PROLOG Programmer Loads facts and rules into the database. Makes queries to the database to see if a fact is: Øin the database or Øcan be implied from the facts and rules therein ---

System Interaction Problem solving in PROLOG 1. insert facts and rules into the database 2. ask questions (queries) based on the contents of the database q Facts Used to represent unchanging information about objects and their relationships. Only facts in the PROLOG database can be used for problem solving. Insert facts into the database by, Ø typing the facts into a file and loading (consulting) the file into a running PROLOG system ---

System Interaction q Queries Retrieve information from the database by entering QUERIES A query, Ø is a pattern that PROLOG is asked to match against the database Ø has the syntax of a compound query Ø may contain variables A query will cause PROLOG to Ø look at the database Ø try to find a match for the query pattern Ø execute the body of the matching head Ø return an answer ---

q Logic Programming q Logic programming is a form of declarative programming q A program is a collection of axioms Each axiom is a Horn clause of the form: H : - B 1, B 2, . . . , Bn. where H is the head term and Bi are the body terms Meaning H is true if all Bi are true q A user of the program states a goal (a theorem) to be proven The logic programming system attempts to find axioms using inference steps that imply the goal (theorem) is true ---

Basic Proof technique - modus ponens A -> B A ----- B ---

q Resolution q To deduce a goal (theorem), the logic programming system searches axioms and combines sub-goals q For example, given the axioms: C : - A, B. D : - C. q To deduce goal D given that A and B are true: Forward chaining (from fact to goal) deduces that C is true: C : - A, B and then that D is true: D : - C Backward chaining (from goal to fact) finds that D can be proven if subgoal C is true: D : - C the system then deduces that the sub-goal is C is true: C : - A, B Since the system could prove C it has proven D ---

q. Prolog Uses backward chaining More efficient than forward chaining for larger collections of axioms q. Interactive (hybrid compiled/interpreted) q. Applications: expert systems, artificial intelligence, natural language understanding, logical puzzles and games ---

PROLOG Paradigm Examples (Facts) English “A dog is a mammal” “A sparrow is a bird” PROLOG isa(dog, mammal). isa(sparrow, bird). ---

PROLOG Paradigm Examples (Rules) English PROLOG “Something is an animal if it is a mammal or a bird” animal(X) : - isa(X, mammal). animal(X) : - isa(X, bird). ---

PROLOG Paradigm Examples (Queries) English PROLOG “is a sparrow an animal? ” answer: “yes” “is a table an animal? ” answer: “no” “what is a dog? ” answer: “a mammal” ? - animal(sparrow). yes ? - animal(table). no ? - isa(dog, X). X = mammal ---

PROLOG syntax q Constants Atoms Ø Alphanumeric atoms - alphabetic character sequence starting with a lower case letter Examples: apple a 1 apple_cart Ø Quoted atoms - sequence of characters surrounded by single quotes Examples: ‘Apple’ ‘hello world’ Ø Symbolic atoms - sequence of symbolic characters Examples: & < > * - + >> Ø Special atoms Examples: ! ; [ ] {} Numbers Ø Integers and Floating Point numbers Examples: 0 1 9821 -10 1. 3 -1. 3 E 102 ---

PROLOG syntax q Variable Names a sequence of alphanumeric characters beginning with an upper case letter or an underscore Examples: Anything _var X _ q Compound Terms (structures) an atom followed by an argument list containing terms. The arguments are enclosed within brackets and separated by commas Example: isa(dog, mammal) ---

Prolog syntax q The names of all relationships and objects must begin with a lower case letter. For example studies, ali, programming q The relationship is written first and the objects are enclosed within parentheses and are written separated by commas. For example studies(ali, programming) q The full stop character ‘. ’ must come at the end of a fact. q Order is arbitrary but it should be consistent ---

Example q Program with three facts and one rule: rainy(columbo). rainy(ayubia). cold(ayubia). snowy(X) : - rainy(X), cold(X). q Query and response: ? - snowy(ayubia). yes q Query and response: ? - snowy(columbo). no q Query and response: ? - snowy(lahore). No q ? - snowy(C). C = ayubia because rainy(ayubia) and cold(ayubia) are sub-goals that are both true facts in the database snowy(X) with X=columbo is a goal that fails, because cold(X) fails, triggering backtracking ---

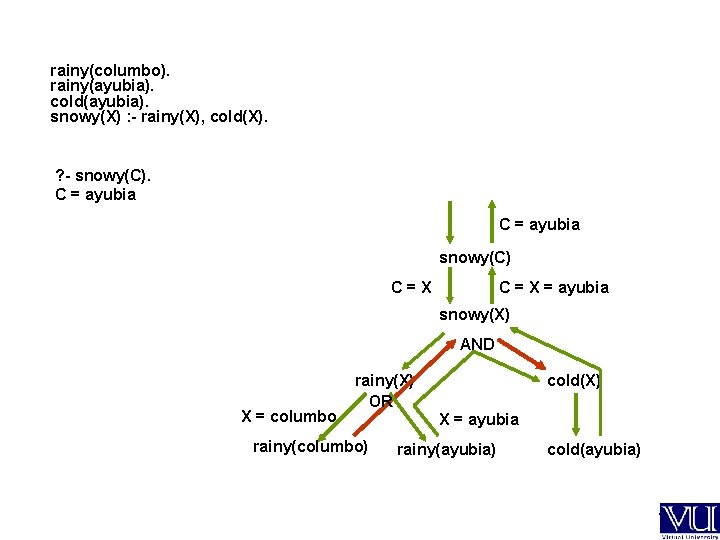
rainy(columbo). rainy(ayubia). cold(ayubia). snowy(X) : - rainy(X), cold(X). ? - snowy(C). C = ayubia snowy(C) C=X C = X = ayubia snowy(X) AND X = columbo rainy(X) OR rainy(columbo) cold(X) X = ayubia rainy(ayubia) cold(ayubia) ---

Logic Representation : Propositional Calculus q Propositional Logic Boolean statements Logic connectives Example – a family Atomic statements p: Ahmed is father of Belal q: Ahmed is brother of Aslam r : Aslam is uncle of Belal Complex statements Statement Logic p Ahmed is not father of Belal p q Ahmed is father of Belal or Ahmed is brother of Aslam p q r If Ahmed is father of Belal and brother of Aslam then Aslam is uncle of Belal ---

Prolog Programming Prolog code Predicate Calculus q Predicates man(Ahmed) father(Ahmed, Belal) brother(Belal, Chand) brother(Chand, Delawar) owns(Belal, car) tall(Belal) hates(Ahmed, Chand) family() Predicates man(symbol) father(symbol, symbol) brother(symbol, symbol) owns(symbol, symbol) tall(symbol) hates(symbol, symbol) family() Clauses man(ahmed). father(ahmed, belal). brother(ahmed, chand). owns(belal, car). tall(belal). hates(ahmed, chand). family(). q Formulae X, Y, Z(man(X) man(Y) father(Z, X) brother(X, Y)) q Variables X, Y and Z brother(X, Y): man(X), man(Y), father(Z, X). q Constants Ahmed, Belal, Chand, Delawar and car Goal brother(ahmed, belal). ---

Sections of Prolog Program (1 -3) q Predicates Declarations of Relations or Rules Just like function prototype (declaration). Zero or more arguments Example Predicates man(symbol) family() a_new_predicate (integer, char) ---

Sections of Prolog Program (2 -3) q Clauses Definition(s) of Predicate = Sentence OR Phrase Types Ø Rules (function definitions) – 0 or more conditions (statements) Ø Facts – 0 conditions – All parameters constant Examples Ø Fact brother(ahmed, chand). Ø Rule brother(X, Y): man(X), man(Y), father(Z, X). ---

Sections of Prolog Program (3 -3) q Goal of inference Only and exactly one instance The only tentative section of the program The main() of prolog Goal truth value = output of program Syntactically and Semantically just another clause Ø Empty, simple (one goal), or compound (sub-goals) Examples Ø Goal brother(X, chand). <or> brother(ahmed, chand). Ø Goal brother(X, chand), father(). ---

Sample Program Update domains person = symbol predicates brother(X, Y): X<>Y, father(Z, X), father(Z, Y). nondeterm father(person, person) nondeterm brother(person, person) nondeterm cousin(person, person) nondeterm grandfather(person, person) cousin(X, Y): father(A, X), father(B, Y), brother(A, B). clauses father(a, b). father(a, c). father(a, d). father(b, e). father(b, f). father(b, g). father(c, h). father(c, i). father(d, j). father(d, k). grandfather(X, Y): father(Z, Y), father(X, Z). goal cousin(X, Y). ---

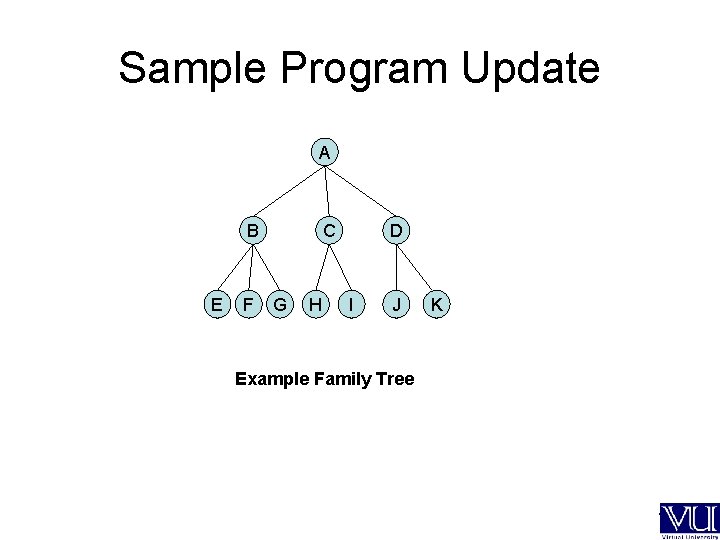
Sample Program Update A B E F C G H D I J K Example Family Tree ---

Prolog Variables q Constant placeholders (NOT variables) Bounded once q Loosely typed q Start with Capital letter or underscore q Examples brother(ahmed, Ahmed) brother(ahmed, _x) Brother(ahmed, X) q Anonymous variable The _ Some value that isn’t required Example brother(ahmed, _) ---

Other Syntactic Elements q Special predicates cut <or> ! not(predicate) q Predefined predicates write(arg 1[, arg 2[, arg 3[, arg 4[…. . ]]]]) nl readint(var) readchar(var) readln(var) … many more related to i/o, arithmetic, OS etc ---

Other Syntactic Elements q. Operators Arithmetic Ø + - * div / mod Relational Ø < <= => > = <> >< q. Additional domains Facts Database ---

PROLOG Lists q Lists a sequence of terms of the form [t 1, t 2, t 3, t 4, . . . , tn] where term ti is the ith element of the list Examples: [a, b, c] is a list of three elements a, b and c. [[a, list, of, lists], and, numbers, [1, 2, 3]] is a four element list. [ ] is the ‘empty list’. It is an atom not a list data type ---

Working with Lists (1 -3) q Compound data type q Arbitrary elements; no size limit q Concise representation in Prolog q head – tail separator [<head>|<tail>] head is an element tail is list of the same sort | is used for list construction as well as list dismantling. q Examples [1, 2, 3] [a, bc, def, gh, i] [ ] ---

Working with Lists (2 -3) q. Examples [a, bc, def, gh, i] [ ] [1, 2, 3] [1, 2 | [3] ] [1 | [2, 3] ] [1, 2, 3 | [ ] ] ---

Working with Lists (3 -3) q Think Recursive! q Example program Domains list = integer * Predicates length (list, integer) Clauses length([], 0). length ([_|Tail], Len): Length (Tail, Tail. Len), Len = Tail. Len + 1. Goal X = [1, 2, 3], length(X, Len). %length of an empty list is zero %getting the tail length %the length of list is 1 plus the length of tail ---

Last and second last element in a list % last. Element(X, L) : - X is the last element of the list L last. Element(X, [X]). last. Element(X, [_|L]) : - last. Element(X, L). last_but_one(X, [X, _]). last_but_one(X, [_, Y|Ys]) : - last_but_one(X, [Y|Ys]). ---

q. Eliminate consecutive duplicates of list elements. If a list contains repeated elements they should be replaced with a single copy of the element. The order of the elements should not be changed. Example: ? - compress([a, a, b, c, c, a, a, d, e, e], X). X = [a, b, c, a, d, e] ---

compress([], []). compress([X], [X]). compress([X, X|Xs], Zs) : - compress([X|Xs], Zs). compress([X, Y|Ys], [X|Zs]) : - X = Y, compress([Y|Ys], Zs). ---

Sorting sorted ([ ]). sorted ([X, Y | list]) : - X <= Y, sorted ([Y | list]). ---

List Membership q List membership is tested with the member predicate, defined by member(X, [X|T]). member(X, [H|T]) : - member(X, T). q ? - member(b, [a, b, c]). q Execution: member(b, [a, b, c]) does not match predicate member(X 1, [X 1|T 1]) member(b, [a, b, c]) matches predicate member(X 1, [H 1|T 1]) with X 1 = b, H 1 = a, and T 1 = [b, c] Sub-goal to prove: member(X 1, T 1) with X 1 = b and T 1 = [b, c] member(b, [b, c]) matches predicate member(X 2, [X 2|T 2]) with X 2 = b and T 2 = [c] The sub-goal is proven, so member(b, [a, b, c]) is proven (deduced) q Note: variables are "local" to a clause (just like the formal arguments of a function) Local variables such as X 1 and X 2 are used to indicate a match of a (sub)-goal and a head predicate of a clause ---

Example of a user-defined data type: set. q set membership -- same as list membership q subset( [ A | X ], Y ) : - member( A, Y ), subset( X, Y ). subset( [ ], Y ). % The empty set is a subset of every set. q intersection % Assumes lists contain no duplicate elements. intersection( [ ], X, [ ] ). intersection( [ X | R ], Y, [ X | Z ] ) : - member( X, Y ), !, intersection( R, Y, Z ). intersection( [ X | R ], Y, Z ) : - intersection( R, Y, Z ). q union( [ ], X, X ). union( [ X | R ], Y, Z ) : - member( X, Y ), !, union( R, Y, Z ). union( [ X | R ], Y, [ X | Z ] ) : - union( R, Y, Z ). ---

The not operator member (Element, [Element | _ ]) : - !. member (Element, [_ | List]) : member(Element, List). member (X, [ 1, 2, 3]). not(member(X, [1, 2, 3]))). ---

Puzzles- Who owns the zebra q. Zebra files ---

Puzzles- Who owns the zebra q Try solving this puzzle on your own. q Now imagine writing a computer program to solve it. q Which was more difficult? q This is an example of a completely specified solution which doesn't appear to be specified at all. The constraints are such that the answer is unique, but they are stated in such a way that it is not at all obvious (to this human, at least) what the answer is. q In Prolog, we could express each of these specifications, then let Prolog's search strategy (database search engine, automated theorem prover) search for a solution. q We don't have to worry about how to solve the problem -- we only have the specify what is to be solved. ---

Zebra Puzzle q. Prolog program ---

Expert system q A simple medical expert system q relieves(Drug, Symptom). relieves(aspirin, headache). relieves(aspirin, moderate_pain). relieves(aspirin, moderate_arthritis). relieves(aspirin_codine_combination, severe_pain). relieves(cough_cure, cough). relieves(pain_gone, severe_pain). relieves(anti_diarrhea, diarrhea). relieves(de_congest, cough). relieves(de_congest, nasal_congestion). relieves(penicilline, pneumonia). relieves(bis_cure, diarrhea). relieves(bis_cure, nausea). relieves(new_med, headache). relieves(new_med, moderate_pain). relieves(cong_plus, nasal_congestion). ---

q aggravates(Drug, Condition). aggravates(aspirin, asthma). aggravates(aspirin, peptic_ulcer). aggravates(anti-diarrhea, fever). aggravates(de_congest, high_blood_pressure). aggravates(de_congest, heart_disease). aggravates(de_congest, diabetes). aggravates(de_congest, glaucoma). aggravates(penicilline, asthma). aggravates(de_congest, high_blood_pressure). aggravates(bis_cure, diabetes). aggravates(bis_cure, fever). ---

should_take(Person, Drug) : complains_of(Person, Symptom), relieves(Drug, Symptom), not(unsuitable_for(Person, Drug)). unsuitable_for(Person, Drug) : aggravates(Drug, Condition), suffers_from(Person, Condition). complains_of(ali, headache). suffers_from(ali, peptic_ulcer). ? - should_take(ali, Drug). Drug = new_med; ---

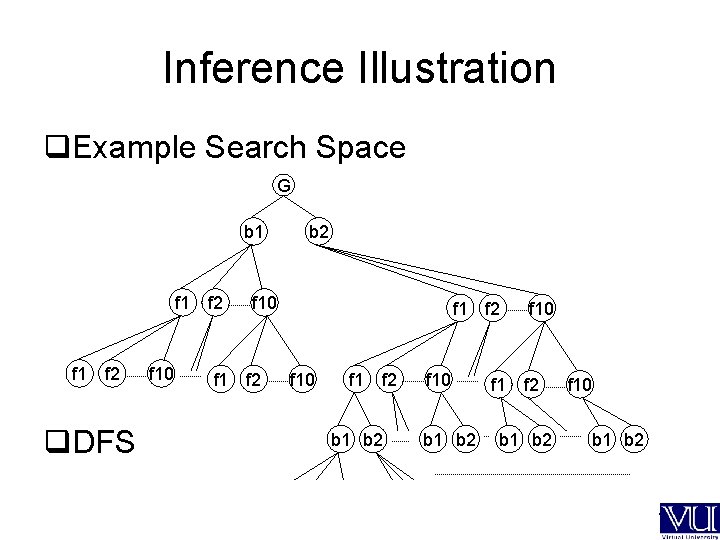
Inference Illustration q. Example Search Space G b 1 f 2 f 1 f 2 q. DFS f 10 b 2 f 10 f 1 f 2 b 1 b 2 f 10 b 1 b 2 ---

Flow Control q q q q The cut Predicate (aka ‘!’) It is actually a goal, not an operator It always succeeds immediately but cannot be re-satisfied through backtracking. As a side-effect, sub-goals to its left in a compound goal also cannot be resatisfied. ---

The cut Predicate a, b, !, c, d. If both a and b succeed but c fails then the whole predicate fails, it is a waste of time to re-satisfy a or b. ---

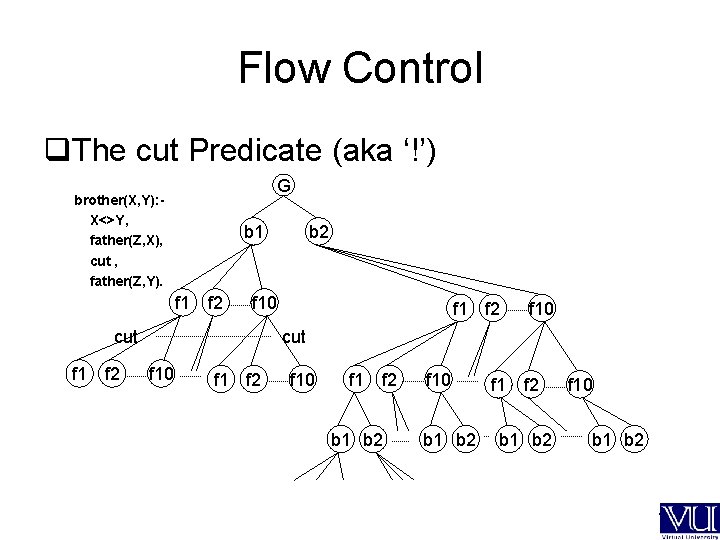
Flow Control q. The cut Predicate (aka ‘!’) G brother(X, Y): X<>Y, father(Z, X), cut , father(Z, Y). b 1 f 2 f 10 cut f 1 f 2 b 2 f 1 f 2 f 10 cut f 10 f 1 f 2 b 1 b 2 f 10 b 1 b 2 ---

Typical Prolog Problem (1 -4) q Implement an INHERITANCE EXPERT SYSTEM that should provide distribution of wealth of a person’s wealth (in Rupees) among his/her inheritors according to the following inheritance law. Person has only one child and that is a daughter then daughter gets 1/3. Person has only daughters (more than one) then daughters get 2/3 total in equal shares. Person has any children then parent gets 1/6 each. Person has no children, no brothers or sisters then mother gets 1/3 and father gets 2/3. Person has brothers and sisters but only one parent alive then parent gets 1/6 and brothers and sisters get 1/6 total in equal shares. Person has children including at least one boy and some amount is left to be inherited according to the above heads (rules), each male child gets twice the amount each female child gets. Any amount that could not be inherited according to the above heads (rules), then government gets all of it. ---

Typical Prolog Problem (2 -4) q Facts D has two wives E and F. D and F had one son A. A married B and then H, B is divorced from C. D and E have two sons C and O. O is married to S the daughter of X , the father and W, the mother. O is also married to P daughter of Q, the father and R, the mother. Q and R have another daughter T. T recently got divorced from U, they have one single son V. C and B have a daughter G. A and H have two sons J and I. I married K and have three children, one boy M and two girls L and N. Q, R, P and E are dead by now. The details of wealth in rupees are, A got 1200, S got 45000 , D got 145, F got 1, J got 10000, K got 10000, L got 10000, T got 10000, Y got 120000, U got 1345340, I got 10000, O got 1234, M got 23000, B got 1050, C got 100 and V got 1234. ---

Typical Prolog Problem (3 -4) q Output of the program Inheritance statement for hameed’s Rs 10000 Statement: <name> Akbar ayesha chawala Ainee Anjum Khalid Government <relation> father daughter son daughter husband none <with> hameed ayesha hameed <amount> Rs. 2304 Rs. 400 Rs. 100 Rs. 5254 End of inheritance statement ---

Typical Prolog Problem (4 -4) q. Procedural Language Implementation Estimated size = 1 kloc Estimated programming time = Estimated Avg. Maintenance time = 1 -5 days q. Prolog Implementation Size =. 4 kloc (approx) programming time = 4 days Avg. Maintenance time = 2 hours ---

Closed World Assumption q q Innocent until proven guilty Actually does not mean innocent if not proven guilty True/Fail system versus True/False Implication ---

Conclusions q q q Declarative Simple concise syntax Built in tree formation and backtracking Readable code Relatively case and type insensitive Suitable for … Problem Solving / Searching Expert Systems / Knowledge Representation Language Processing / Parsing and NLP Game Playing q q Efficiency Left Recursion Double trouble; learning curve Lack of standardization ---

Books q. Prolog Programming for AI by Ivan Bratko q. Visual Prolog; Language Tutorial by PDC ---

Compilers q. PDC Visual Prolog q. SWI Prolog q. Bin-Prolog q. K-Prolog q. Prolog ++ q. Many more… ---